对数与对数函数（高中）

贡献者：欄、停敘

预备知识 1　函数，函数的性质，指数函数

　　在数学的发展历史中，人类不断探索更高效的工具来描述和解决问题。对数（logarithm）便是其中的一种，它将是高中阶段唯一一个在之前从未接触过的运算，它通过独特的方式将乘法与指数的复杂性转化为加法的简便。这不仅是一种运算规则，更是一种观察和理解世界的新视角。

　　在实际应用中，对数具有广泛而深远的意义。例如：

在金融学中，对数被用于分析复利增长和投资回报。例如，计算一笔投资在复利条件下的增长年限时，对数公式能提供直接解答。
在声学中，分贝是基于对数定义的单位，用于衡量声音的强度。它能够压缩声音幅度的巨大变化，使得差异更加直观。
在地质学中，地震的强度以里氏震级表示，其计算公式同样基于对数。这使得地震强度能够跨越多数量级进行比较。
在视觉化数据时，对数可以缩放比例尺。当数据的变化范围极为广泛（例如，人口数量或天体距离）时，使用普通的线性刻度往往难以呈现出数据的细微差异。而对数刻度通过压缩较大的数值范围，使得相对差异更加清晰。

　　对数与指数有着密切的联系。从本质上说，对数运算是指数运算的逆过程。例如，已知 $2^3 = 8$，则对数运算有 $\log_2 8 = 3$，这表示：以 2 为底数，需要乘几次才能得到 8？这一反向关系使得对数成为研究指数增长现象的重要工具。而对数的性质，也使得乘法与加法的转换成为可能。

　　下面的内容将会以三个知识点为主要内容展开，分别是：对数运算、自然常数以及对数函数。由于基本都是新内容，因此篇幅会比较长，但彼此都是贯通的，因此先把对数运算熟练理解，再看后面的内容就会事半功倍。

1. 引入对数运算

　　与早已烂熟于胸的加、减、乘、除和乘方、开方，对数是一个陌生的运算。很多教材会从指数运算的前提下去介绍，说他是指数运算的逆运算。但对数运算本身是远早于指数运算出现的，直接从指数去介绍或许会降低陌生的感觉，但很容易造成理解上的困惑。下面会从对数运算诞生的思路去介绍它。

　　对数运算最早是为了算两个数的乘法而创造出来的。那时还没有计算器，小一点的数当然可以用乘法口诀，但如果想要计算两个位数特别多的数相乘，比如两个四位数相乘，列竖式的方法需要计算四次乘法和四次加法，这显然太麻烦，而且太容易出错了。

　　 John Napier 考虑了这样一个场景：一个点沿着直线在匀速运动，另一个点在线段上运动，它运动的速度与剩下到终点的距离正相关。这样两个点是一一对应的，假设与点 $n$ 对应的另一个点是 $L_n$，线段的长度是 $L$，认为在单位时间内点是匀速的，也就是单位时间内运动的长度树枝上等于这段时间内的速度 $v_n$，即将到来的这一段的速度与此时剩下的距离成正比 $\displaystyle v_{n}=\frac{L_{n-1}}{L}$，从而有：

\begin{equation} L_{n}=L_{n-1}-v_{n}=L_{n-1}(1-\frac{1}{L})\implies\frac{L_{n}}{L_{n-1}}= \frac{L-1}{L}~. \end{equation}

这个比例和 $n$ 无关，也就是说每一段已走过的长度与上一段都是等比例变化的。设初始长度为 $L_{0}=L$，从而根据现在熟悉的幂运算有：

\begin{equation} L_n={L_{n}\over L_{n-1}}\cdot{L_{n}\over L_{n-1}}\cdots{L_{2}\over L_{1}}\cdot{L_{1}\over L_{0}}\cdot L_0=L\cdot(1 - \frac{1}{L})^n~. \end{equation}

　　实际使用时，比如要计算两个数 $L_n,L_m$ 的乘积，只需要根据他的表格找到对应的 $n,m$，求和后再反查找到对应的 $L_{n+m}$ 就可以得到计算的积了，根据指数运算法则，也就是：

\begin{equation} L_nL_m=L^2(1 - \frac{1}{L})^{n+m}~. \end{equation}

注意右侧的表达式，$L^2$ 使得右侧并不符合 $L_{n+m}$ 的表达式 $\displaystyle L(1 - \frac{1}{L})^{n+m}$。John Napier 根据自己的思路提出了他的对数表，顺带还正式使用了小数点。在制作表时，为了使精度提高，他选择取 $L=10^7$，得到了六位数乘法的结果，也避免了式 3 中 $L^2$ 带来的问题，因为此时二者只是在小数点的位置上有区别，而忽略小数点时，则数值相同。

　　而 “对数” 其实是 “比例对数” 的简称，指的就是 “按照比例制作的，对着查表的数”。也就是上面右边的指数 $n$ 是等式左边的数 $L_n$ 的对数，指数运算中，结果称为真数，或者说下面介绍的对数运算中的真数，之所以称为真数，也是因为它是原本要进行乘法计算的 “真实的数字”。当然，Napier 实际制作表的考量很多，这里给出的只是主要思想。

2. 对数运算

　　相信上面的例子已经让你察觉了，指数运算中的指数是真数的对数。而现代数学中的对数也不再是如当初一样查表来定义，现在对数运算的定义是基于幂运算的。

定义 1　对数运算

　　形如

\begin{equation} b=\log_ac~. \end{equation}

的运算称为对数运算。$\log$ 称为对数运算符。这里的变量与定义 1 处是一样的。其中 $a$ 称为底数，$b$ 称为指数，而 $c$ 称为真数。另外：

$ \mathrm{e} $ 为底的对数 $\log_{ \mathrm{e} } c$ 称为自然对数，记作 $\ln c$¹；
$10$ 为底的对数 $\log_{10} c$ 称为常用对数，记作 $\lg c$²；
$2$ 为底的对数 $\log_{2} c$ 在计算机科学中经常使用。

　　对数符号的写法与已有的所有写法都不太像，需要习惯一下。由于上面定义中的 $a,b,c$ 与指数运算对应，将对数代入 $c=a^b$ 的指数之后可以发现：

\begin{equation} a^{\log_a c}=c\qquad \log_a a^b=b~. \end{equation}

　　这说明对数运算和指数运算互为逆运算。如果感觉一会儿是 $c$，一会儿是 $b$，与以往的逆运算有所不同，有点怪。其实，那是因为加法和乘法有交换律，而对数和指数运算没有交换律（即交换底数和真数后，运算结果不会保持不变）。可以这样理解：对于乘法和除法，$m$ 乘以 $a$ 再除以 $a$，原本的数 $m$ 不变，因为两者互为逆运算，因子 $a$ 被 “抵消” 了。而这里，$m$ 对一个数 $a$ 做指数运算，再取 $a$ 的对数，结果仍然是 $m$，因为指数和对数互为逆运算，“消掉” 了底数 $a$。反过来，先对 $m$ 取 $\log a$，再作为 $a$ 的指数运算，结果也是 $m$。这说明对数是指数的逆运算，而非幂的逆运算，运算中抵消的部分是底数，计算始终围绕着指数和真数。

　　定义要求 $a\in\mathbb (0,1)\cup(1,+\infty),c>0$，这样的要求是因为：

当底数 $a = 1$ 时，指数运算 $a^x$ 会始终等于 $1$，无法满足对数的是指数的逆运算的需求。
如果底数为负数，乘方的结果在实数范围内可能会得到负数甚至复数，这样的运算结果无法在实数范围内定义。
指数运算的结果总是正数，因此真数 $c$ 也必须是正数。

　　总的说来，当前所有的限定都是为了在实数的范畴内能满足指数与对数的互逆关系。

　　根据指数函数可以得到，对数运算有两个特殊的计算结果：$\log_a a=1,\log_a1=0$。下面给出对数运算的法则。仍然，不需要考虑怎么证明³，实际使用时，可以将某个变量代入幂运算的结果，可以得到倒数、减法等形式：

定理 1　对数运算法则

乘法法则：$\log_a(xy)=\log_ax+\log_ay$
换底公式：$\displaystyle \log_a b=\frac{\log_cb}{\log_ca}$
幂法则：$\displaystyle \frac{m}{n}\log_a b=\log_{a^n} b^m$

　　这三个公式非常重要，几乎所有的对数运算都离不开它们，请务必熟练使用。第一个公式可以将对数内的乘法拆解成对数外的加法。这一性质在计算复杂表达式的对数时非常实用，比如分解为多个较小的对数进行逐步处理。第二个公式通常会选择某一个特定的底数来实现，这样，只需知道某种特定底数（如：$\ln$ 等）的对数值，就可以计算出任意底数的对数。这种方法常用于将对数统一为可直接查表或利用计算器计算的形式。第三个公式解释了对数内部的幂次运算如何转化为对数外的乘法因子——对数内部的幂次，可以拿到对数外面称为乘法的因子，底数在分母、真数在分子。从换底公式的角度也可以理解这一性质。换底后，对数的底数和真数在分母和分子的相对位置与此公式一致，因此两者的逻辑是一致的。这一公式使得对数与指数运算相结合，便于处理包含幂的对数表达式。

　　另外公式间也可以组合，比如乘法法则与幂法则结合可以得到 $\displaystyle\log_a\left({x\over y}\right)=\log_a\left(xy^{-1}\right)=\log_ax-\log_ay$。

例 1　设 $a=\lg2,b=\lg3$，用 $a,b$ 表示 $\log_5 12$。

　　 $$ \begin{split} \displaystyle \log_5 12&={\lg12\over\lg5}\\ &={\lg (2^2\cdot3)\over \displaystyle\lg{10\over2}}\\ &={2\lg2+\lg3\over 1-\lg2}\\ &={2a+b\over 1-a}\\ \end{split}~. $$

　　例 1 也意味着，可以通过质因数分解，来将某些较大数的对数值，分解为几个质因数的组合，体现了质数的重要性。

3. 自然常数 $ \mathrm{e} $

　　在这里，需要引入一个新的常数——自然常数（natural constant） $ \mathrm{e} $（也称为自然底数⁴（base of the natural logarithm），或欧拉数（Euler’s number））。这是数学中继小学阶段首次接触的 $\pi$ 之后，另一个广为人知的特殊常数。$\pi$ 和 $ \mathrm{e} $ 之间存在许多相似之处也存在紧密的联系，下面会逐步介绍。

引入 $ \mathrm{e} $

　　自然常数一般会通过下面这个例子来引入。假设在银行存入 $1$ 元，银行承诺年利率为 $100\%$，利息的计算公式是 “$\text{利息}=\text{本金}\times\text{年利率}\times\text{存款年数（时间）}$”。下面的计算不要关注每次计算的得到的数值，而是要关注计算过程的变化整合。

　　最简单的情况是银行一年只结算一次利息，这时年末得到的收入就是 $1\times100\%\times1=1$。这样，一年后 1 元会变成 $1+1\times100\%=1\times(1+100\%)^1=2$ 元。

　　如果要求银行 “每半年结算一次利息”，这样计算的好处是，第一次结算之后的利息会作为本金参与到第二次的计算中。于是第一次结算时，利息为 $\displaystyle1\times100\%\times\frac{1}{2}=0.5$。第二次计息时的本金变成了 $\displaystyle1+1\times100\%\times\frac{1}{2}=1.5$。第二次的利息就是 $\displaystyle(1+1\times100\%\times\frac{1}{2})\times100\%\times\frac{1}{2}=\frac{1.5}{2}=0.75$。于是最终的收入变成了 $\displaystyle1+1\times100\%\times\frac{1}{2}+(1+1\times100\%\times\frac{1}{2})\times100\%\times\frac{1}{2}=\frac{1.5}{2}=2.25$。相比第一次多出来的那 $0.25$ 就是因为计息次数变多带来的⁵。整理一下其实就是 $1\times(1+\frac{100\%}{2})^2=2.25$。

　　可以自己试一试 “每三个月一次” 和 “每个月一次”，整理后从银行取出的金额 $A(n)$ 都会变成如下的形式：

\begin{equation} A(n)=a\times\left(1+\frac{1}{n}\right)^n~. \end{equation}

其中 $a$ 是本金，$n$ 是一年计息的次数。

　　上面算过 $A(1)=2,A(2)=2.25$，另外上面提到的 “每三个月一次” 和 “每个月一次” 分别对应 $A(4)\approx 2.4414$、$A(12)\approx 2.6130$。可以看出 $A(n)$ 似乎是不断递增的，于是不禁要问，这个函数会一直递增吗？有没有最大值？通过计算器计算可知每天一次、小时一次和每秒一次分别是 $A(365)\approx 2.7146$、$A(8760)\approx2.7181$、$A(31536000)\approx 2.718266$。看上去好像逐渐停止在小于 $2.72$ 的某个数字了，但如果仅凭这样的直觉，可能会出错⁶。

　　数学家们证明了，这个函数是一直递增的，而且有一个上限，称这个函数的上限⁷为自然常数（Natural Constant），也称作欧拉数（Euler's number），记作 $ \mathrm{e} $，定义为：

\begin{equation} \mathrm{e} = \lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^n~. \end{equation}

如果看不懂这个表达方式没问题，只需要理解它是上面那个存款过程的最终结果，是一个常数，就可以。它描述了增长速度的极限，不仅与利息有关，它还出现在很多自然现象中，简单来说，$ \mathrm{e} $ 代表着在不受限制的情况下，某种东西增长到最快时能达到的程度。

回看 Napier 的对数表

　　在有了 $ \mathrm{e} $ 之后，回看 Napier 提出的对数表，会惊奇的发现其中也有 $ \mathrm{e} $ 的身影。根据式 2 可以得到：

\begin{equation} {L_n\over L}=((1-{1\over L})^{-L})^{-{n\over L}}~. \end{equation}

　　 Napier 选取的 $L=10^7$ 这个非常大的数，使得 $(1-{1\over L})^{-L}$ 的数值非常接近 $ \mathrm{e} $，即：

\begin{equation} {L_n\over L}\approx \mathrm{e} ^{-{n\over L}}\iff-{n\over L}\approx\ln{L_n\over L}~. \end{equation}

　　这意味着，他当时求出来的 $(L_n,n)$ 对数表，几乎和现在常用的自然对数表一模一样。另外，可以记忆一下几个特殊的自然对数值：$\ln2\approx0.7,\ln3\approx1.1,\ln5\approx1.61$。

对比 $ \mathrm{e} $ 与 $\pi$

　　自然常数 $ \mathrm{e} \approx 2.71828$，它和早已在小学时就接触过的 $\pi$ 有许多相似点。

　　他们都是无理数，这意味着它们不能表示为两个整数的比值。它们的小数部分是无限且不循环的，也就是说，在任何整数进制中它们都永远不会终止或重复。

　　他们也都是超越数，意思是它们不能作为任何有理方程的解。换句话说，这比无理数的要求更加严格。它们不仅不能表示为整数之比，也不能通过各阶的根式表示。$ \mathrm{e} $ 的超越性由查尔斯·埃尔米特（Charles Hermite）在 1873 年证明，$\pi$ 的超越性由费迪南德·冯·林德曼（Ferdinand von Lindemann）在 1882 年证明。

　　二者都可以用无穷展开的方式来表示，下面给出两个常见的展开方式⁸：

\begin{equation} \pi=4\sum_{n=0}^\infty\frac{(-1)^i}{2i+1}~. \end{equation}

\begin{equation} \mathrm{e} =\sum_{n=0}^\infty\frac{1}{i!}~. \end{equation}

　　 $ \mathrm{e} $ 的定义有很多种方式，除了之前提到的广为了解的极限定义。下面将给出另一个定义：$ \mathrm{e} $ 是使得

\begin{equation} f'(x) = f(x)~. \end{equation}

成立的指数函数的底数，这意味着以 $ \mathrm{e} $ 为底的指数函数是唯一的能够保持自身增长速度不变的函数。

　　另外，二者也有相当紧密的联系，在复变函数中出现的欧拉公式 $ \mathrm{e} ^{ \mathrm{i} \pi} + 1 = 0$，常被人们称为最优雅的数学公式，它将这两个常数联系在了一起。

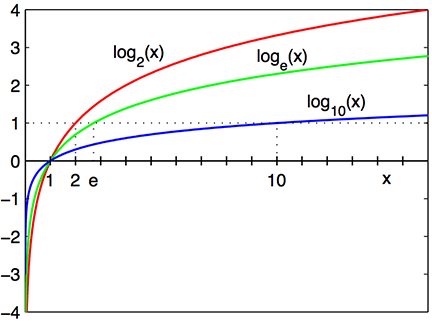
4. 对数函数及性质

定义 2　对数函数

　　形如

\begin{equation} f(x) = \log_a x~. \end{equation}

的函数称作对数函数（logarithmic function），其中 $a\in\mathbb (0,1)\cup(1,+\infty)$。

　　在对数函数的性质部分，读者仍可以按照之前研究幂函数与指数函数的方式去研究，但由于对数函数与指数函数互为反函数⁹，即二者的图像关于 $y=x$ 对称。因此，可以直接将之前研究过的指数函数的性质对称得到对数函数的性质，下面所有的性质都与之前介绍的指数函数性质对应出现：

函数的定义域是 $(0,+\infty)$，值域是 $\mathbb{R}$，函数恒过定点 $(1,0)$。
$a>1$ 时，函数在定义域上是递增的；反之 $0< a<1$ 时，函数则是递减的。
在 $y>0$ 时，如果从左到右画一条水平线，则会先穿过 $a$ 值较小的函数图象，后穿过 $a$ 值较大的函数图象；在 $y<0$ 时，从左到右画一条水平线，则会先穿过 $a$ 值较大的函数图象，后穿过 $a$ 值较小的函数图象。在 $0< x<1$ 时，如果从下到上画一条垂线，则会先穿过 $a$ 值较大的函数图象，后穿过 $a$ 值较小的函数图象；在 $x>1$ 时，从下到上画一条垂线，则会先穿过 $a$ 值较小的函数图象，后穿过 $a$ 值较大的函数图象。
若 $a>1$，则 $0< x<1$ 时，$y<0$，$x>1$ 时，$y>0$；若 $0< a<1$，则 $0< x<1$ 时，$y>0$，$x>1$ 时，$y<0$。
任意的底数 $a$ 都可以通过伸缩变换来表示所有的对数函数，这也表明不同对数函数之间存在放缩关系。
$y$ 轴（也就是直线 $x=0$）是函数的一条渐近线，对应 $x$ 趋于 $0$ 时。

　　函数图如图 1 。

图 1：几种不同底的对数函数

未完成：这里的图只有 $a>1$ 的。

5. 指数函数与对数函数的相似性

预备知识 2　函数的变换（高中），导数（高中）

　　根据幂运算和对数运算的法则，任意 $f(x)=a^x$ 都可以变形，得到：

\begin{equation} f(x)=e^{x\ln a}~. \end{equation}

　　即，所有的指数函数都可以由 $ \mathrm{e} ^x$ 通过在 $x$ 方向上伸缩或关于 $y$ 轴对称（$\ln a<0$ 时）得到，或者所有的指数函数 $a^x$ 都可认为是 $f(x)=e^x$ 与 $g(x)=x\ln a$ 复合得到的 $f(g(x))$。

　　同理，根据对数运算的性质，任意 $f(x)=\log_ax$ 都可以变形，得到：

\begin{equation} f(x)=\frac{1}{\ln a}\ln x\iff f(x)\ln a=\ln x~. \end{equation}

　　即，所有的对数函数都可以由 $\ln x$ 通过在 $y$ 方向上伸缩或关于 $x$ 轴对称（$\ln a<0$ 时）得到，或者所有的对数函数 $\log_ax$ 都可认为是 $f(x)=\ln x$ 与 $\displaystyle g(x)=\frac{x}{\ln a}$ 复合得到的 $g(f(x))$。同时，这个结论也可由指数函数和对数函数在参数相同时互为反函数验证。

　　综上，所有的指数函数、对数函数之间都是相似的。根据上述关系，已知 $\left( \mathrm{e} ^x\right)'= \mathrm{e} ^x,\left(\ln x\right)'=\frac{1}{x}$，根据复合函数求导法则，可知：

\begin{equation} \left(a^x\right)'=\ln a\cdot \mathrm{e} ^x~,\left(\log_a x\right)'=\frac{1}{x\ln a}. \end{equation}

　　而正是因为上面提到的这些相似的关系，以及求导时的特性，才使得 $ \mathrm{e} $ 这个常数如此 “自然”。

1. ^ 在实际使用时，尽管它不叫常用对数，但它其实是理论推导时最常用的，以至于在很多大学教材或论文中如果不写底数则默认是指自然对数，即 $\log c$ 一般是指 $\ln c$
2. ^ 生活中常见的分贝、地震级别等都使用常用对数
3. ^ 在高中阶段他们的证明都是基于指数运算的。
4. ^ 关于为什么叫自然底数，可以参考子节 5 。
5. ^ 因此银行也会调低短期存储的利率，以降低短期储蓄的收入来保证长期投资的权益。
6. ^ 比如 $\displaystyle1\over n$ 这样不断求和之后，其实不会停在某个范围内，而是会发散出去。
7. ^ 确切的说叫上确界。
8. ^ 关于求和符号可以参考求和符号（高中），关于阶乘可以参考阶乘（高中）。
9. ^ 这一点可以根据对数和指数函数互为逆运算的性质来自行验证。