群的同态与同构

                     

贡献者： 叶月2_; JierPeter; addis

预备知识　正规子群

1. 同构

　　 让我们来观察两个群 $(\mathbb{Z}, +)$ 和 $(2\mathbb{Z},+)$。如果我们把 $2\mathbb{Z}$ 中的 $2$ 都看成 $1$，$4$ 都看成 $2$，以此类推，将 $2k$ 都看成 $k$，那么两个群的运算规则是一模一样的。比如说，$2\mathbb{Z}$ 中有 $2+4=6$，对应的是 $\mathbb{Z}$ 中 $1+2=3$ 的等式。

　　 我们研究集合和群的时候，元素叫什么名字并不重要，重要的是元素之间是否相同以及运算规则是怎样的。那么，如果我们真的将 $2\mathbb{Z}$ 中的元素 $2k$ 都重命名为 $k$，它就和 $\mathbb{Z}$ 没什么区别了。所以在群的意义上，如果不考虑子群关系，单独把 $\mathbb{Z}$ 和 $2\mathbb{Z}$ 拿出来的时候，我们就认为它们是不可区分的，完全相同的两个群。

　　 如果我们建立一个映射 $f:\mathbb{Z}\rightarrow2\mathbb{Z}$，定义为 $f(k)=2k$，那么这个 $f$ 就是一个双射，它在两个群的元素之间一一对应地建立了联系。这样，对于任意整数 $m, n$，有 $f(m)+f(n)=f(m+n)$，也就是说 “先运算再映射” 和 “先映射再运算” 结果是相同的。

　　 类似地，对于任意的两个群 $G$ 和 $K$，如果存在一个双射 $f:G\rightarrow K$，使得对于任意的 $x, y\in G$ 都满足 $f(x)f(y)=f(xy)$，那么这两个群的运算结构就是一模一样的。这时我们说这两个群是同构（isomorphic）的，而这个使得它们同构的双射就被称为 $G$ 和 $K$ 之间的同构映射（isomorphic mapping），也可以简称同构（isomorphism）这里加粗的两个 “同构”，前者是形容词，后者是名词。

定义 1　自同构

　　 称群到自身的同构为一个自同构（automorphism）1。

　　 群 $G$ 的全体自同构配合映射的复合，又构成一个群，称为 $G$ 的自同构群，记为 $ \operatorname {Aut}(G)$。

　　 由于同构使得两个群各方面表现一模一样，研究同构其实没有太大意义，我们甚至直接把同构的两个群看成同一个群，不管元素具体怎么命名的。有意思的结构，是以下定义的 “同态映射”。

2. 同态

　　 同构映射是一个双射。如果把这个要求拿掉，我们就得到同态的概念：

定义 2　同态映射

　　 对于两个群 $G$ 和 $K$，如果映射（不一定是双射）$f:G\rightarrow K$ 使得 $\forall x, y\in G, f(x)f(y)=f(xy)$，那么称 $G$ 和 $K$ 是同态（homomorphic）的，称 $f$ 是同态映射（homomorphic mapping）或同态（homomorphism）。

定义 3　像和核

　　 沿用定义 2 的设定。$K$ 中被映射到的元素构成的集合，称为 $f$ 的像（image），记作 $f(G)$。$G$ 中映射到 $K$ 的单位元 $e_K$ 的元素构成的集合，称为 $f$ 的核（kernal），记为 $\ker(f)$。

　　 注意，$f(G)\subset K$，$\ker(f)\subset G$。

　　 同态的两个群，运算结构很相似但又不完全一样。在以上定义的例子中，$K$ 的行为就像是一个弱化版的 $G$，可能会丢失一些细节，但保留的方面和 $G$ 是一模一样的。这么说可能不够具体，我们用习题 1 和习题 2 来理解同态的 “似而不同”。

习题 1　

　　 设两个群 $G$ 和 $K$，$f:G\rightarrow K$ 是一个同态，$x\in G$，求证 $f(x^{-1})=(f(x))^{-1}$。

习题 2　群同态基本定理

　　 设两个群 $G$ 和 $K$，$f:G\rightarrow K$ 是一个满同态。求证：

  1. $\ker(f)$ 是 $G$ 的一个正规子群2。
  2. 对于 $x_1, x_2, y_1, y_2\in G$，如果3$x_1^{-1}x_2\in \ker(f)$ 和 $y_1^{-1}y_2\in \ker(f)$，那么 $f(x)=f(x_1)$，$f(y)=f(y_1)$。
  3. 由前两条的结论，证明可以用 $f$ 来导出一个映射 $f': G/\ker(f)\rightarrow K$，它是一个群同构。

　　 由习题 2 ，同态的实质就是商群 $G/\ker(f)$ 和 $K$ 之间的同构。$G/\ker(f)$ 继承了 $G$ 的运算，但是由于把同余的元素全都当作同一个了，也就丢失了一部分细节。因此我们说同态的两个群也是 “似而不同” 的。

　　 对于两个存在满同态关系的群，我们可以利用群同态定理，进一步找到结构上的相似之处。

定理 1　

　　 设 $f:G_1\to G_2$ 是满同态，$N= \operatorname {ker}f$，则

  1. 若 $B$ 是 $G_1$ 的子群，则 $f(B)$ 是 $G_2$ 的子群。反之，若 $K$ 是 $G_2$ 的子群，则 $f^{-1}(K)=\{x\in G_1\mid f(x)\in K\}$ 是 $G_1$ 的子群且 $f^{-1}(K)\supseteq N$。
  2. 对于任意 $H\supseteq N,f:H\to f(H)$ 建立了子群之间的一一对应；在该双射下，$H\lhd G_1$ 当且仅当 $f(H)\lhd G_2$。
  3. $H$ 同上设。$G_1/H\cong G_2/f(H)$。

　　 证明：

  1. 设任意 $f(x),f(y)\in f(B)$，则 $f(x)f(y)^{-1}=f(xy^{-1})$。又因为 $xy^{-1}\in B$，所以 $f(xy^{-1})\in f(H)$。所以 $f(B)$ 是 $G_2$ 的子群。反之也同理易证 $f^{-1}(K)$ 是 $G_1$ 的子群4。设 $e'=f(e)$，由于 $e'\in K$，所以 $f^{-1}(e')=N\subseteq f^{-1}(K) $。
  2. 由前文讨论可知，$f(H)$ 必然是 $G_2$ 的子群，因此 $f^{-1}f(H)$ 必然是包含 $N$ 的子群。所以 $f$ 确实建立了包含 $N$ 的 $G_1$子群集合与 $f(H)$ 构成的子群集合之间的映射。在该集合意义上，$f$ 是满射（$f^{-1}f(H)\supseteq H,N$），所以接下来我们只需要证明这是单射即可。
    假设这不是单射，即至少存在两个包含 $N$ 的子群 $A,B$ 使得 $f(A)=f(B)$。对于任意 $a\in A$，存在 $b\in B$ 使得 $f(a)=f(b)$，则 $f(ab^{-1})=e'$，所以 $ab^{-1}\in N\subseteq B$，则 $a\in B, A\subseteq B$。反之，对于任意 $b'\in B$，存在 $a'\in A$ 使得 $f(a'b'^{-1})=e'$，则 $a'b'^{-1}\subseteq A$，则 $b'\in A,B\subseteq A$，所以 $A=B$，映射是单射；
    下面证最后一个性质。设 $H\lhd G_1$。对于任意 $f(a)\in G_2$ 有 $f(a)f(H)f(a)^{-1}=f(aHa^{-1})=f(H)$，因此 $f(H)\lhd G_2$。反之由 $f$ 是满同态，易证若 $K\lhd G_2$，则 $f^{-1}(K)\lhd G_1$。
  3. 由上文知 $f(H)\lhd G_2$。现设 $f'=\pi \circ f:G_1\to G_2\to G_2/f(H)$5。这是满同态的复合，因此 $f'$ 也是满同态。因为 $ \operatorname {ker}f'=f^{-1}f(H)=H$，由群同态基本定理得证此条性质。

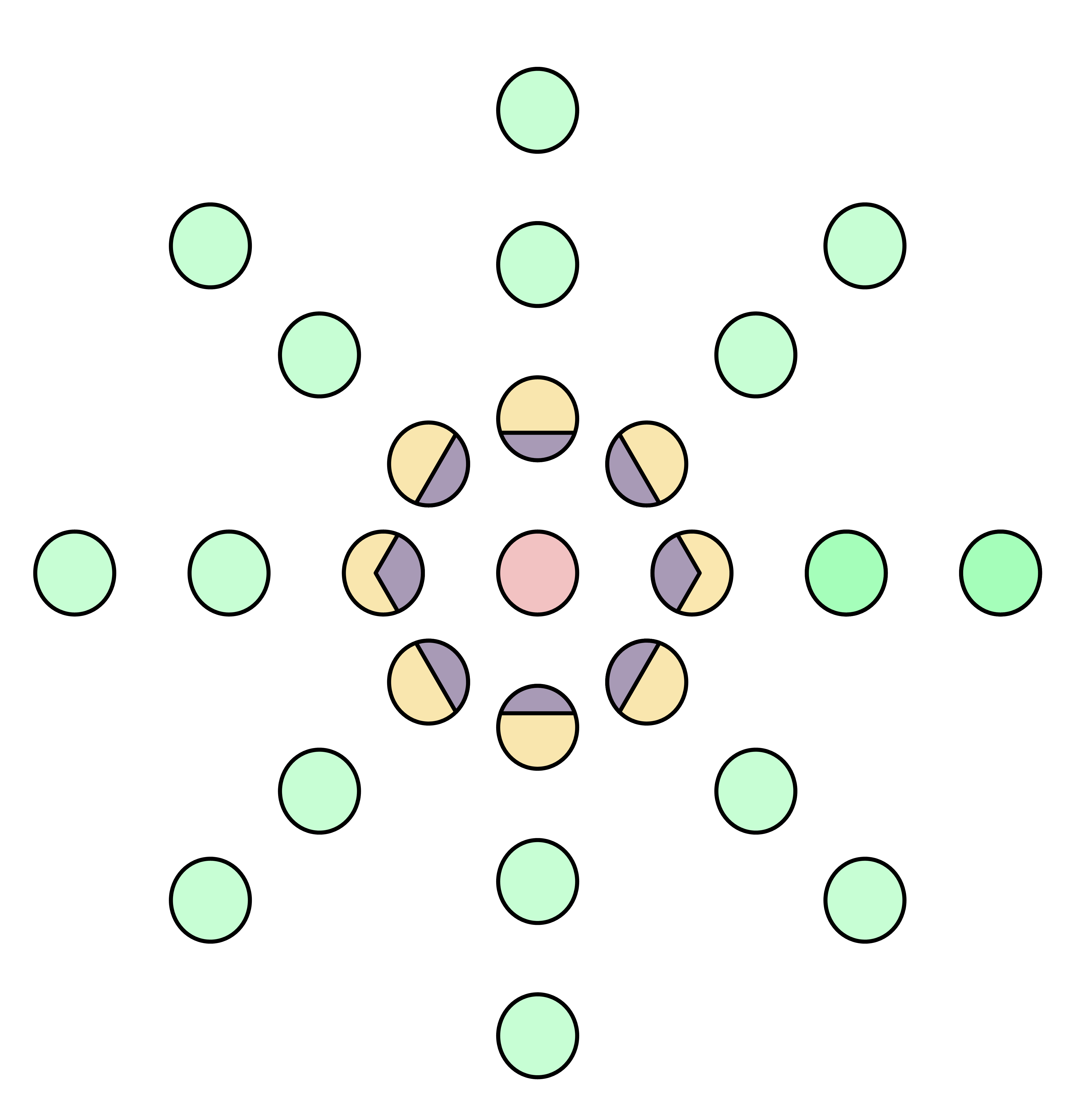
　　 应用定理 1 在自然同态 $\pi:G\to G/N$ 上，可以清楚看到，商群是如何继承原群结构的，具体如下图所示。

图
图 1：正规子群的一一对应。红色圆代表正规子群 $N$，所有圆都是群 $G$ 关于 $N$ 的陪集分解。紫色部分加上红色圆代表在群 $G$ 意义上的正规子群 $N_2$，$N_2\supseteq N$。黄色圆加上红色圆则代表在商集意义上的正规子群，即 $N_2/N\lhd G/N$。

推论 1　

　　 $G$ 是群，若 $H,N$ 都是 $G$ 的正规子群且 $H\supseteq N$，我们有6

\begin{equation}G/H\cong (G/N)/(H/N)~.\end{equation}

3. 内自同构和外自同构

　　 回顾线性代数中的知识：给定线性空间的基以后，线性变换和矩阵就一一对应（我们称之为给定基下用矩阵表示线性变换），而改变基以后同一个线性变换的基也会变。因此，群 $(\{\text{线性变换}\}, \text{映射的复合})$ 与群 $(\{\text{矩阵}\}, \text{矩阵乘法})$ 之间可以建立同构。这样的同构不是唯一的，而是依赖于基的选择。

　　 不同的矩阵可以看成同一个线性变换在不同基下的表示，也可以看成两个不同的线性变换在同一个基下的表示。因此，我们可以用一个基来将矩阵对应到线性变换上，再用另一个基将线性变换对应到另一个矩阵上，由此就得到了矩阵之间的对应，这个对应就是矩阵乘法群到自身的同构。同一个线性变换在不同基之间的矩阵表示的关系是相似，具体参见过渡矩阵小节。

　　 由上段论述可知，给定可逆矩阵 $ \boldsymbol{\mathbf{Q}} $，则矩阵到自身的映射 $f$ 是一个自同构，其中 $f( \boldsymbol{\mathbf{M}} )= \boldsymbol{\mathbf{Q}} ^{-1} \boldsymbol{\mathbf{MQ}} $。这提示我们一种构建群自同构的方法。

定义 4　内自同构

　　 给定群 $G$。取 $g\in G$，定义映射 $ \operatorname {Ad}_g:G\to G$ 如下：对于任意 $x\in G$，都有 $ \operatorname {Ad}_g(x)=gxg^{-1}$。

　　 称 $ \operatorname {Ad}_g$ 是 $G$ 上的内自同构（inner automorphism），或者共轭自同构（cogredient automorphism）。

　　 群 $G$ 的全体内自同构构成 $ \operatorname {Aut}(G)$ 的一个子群，称为 $G$ 的内自同构群，记为 $ \operatorname {Inn}(G)$。

定理 2　

　　 内自同构群是自同构群的正规子群。

　　 证明：

　　 给定群 $G$，设 $f\in \operatorname {Aut}(G)$。任取 $g, x\in G$，则由习题 1 可得，

\begin{equation} \begin{aligned} f^{-1} \left(gf(x)g^{-1} \right) &=f^{-1} \left(g \right) f^{-1} \left(f(x) \right) f^{-1} \left(g^{-1} \right) \\ &=f^{-1} \left(g \right) xf^{-1} \left(g^{-1} \right) \\ &=f^{-1} \left(g \right) x \left(f^{-1} \left(g \right) \right) ^{-1} \end{aligned}~ \end{equation}

　　 由 $x$ 的任意性，式 2 意味着 $f\circ \operatorname {Ad}_g\circ f^{-1}= \operatorname {Ad}_{f^{-1}(g)}$。因此 $f\circ \operatorname {Inn}(G)\circ f^{-1}\subseteq \operatorname {Inn}(G)$，故 $ \operatorname {Inn}(G)$ 是 $ \operatorname {Aut}(G)$ 的正规子群。

　　 证毕。

　　 由定理 2 ，我们可以计算商群 $ \operatorname {Aut}(G)/ \operatorname {Inn}(G)$。

定义 5　外自同构

　　 给定群 $G$，称 $ \operatorname {Aut}(G)/ \operatorname {Inn}(G)$ 为 $G$ 的外自同构群（outer automorphism），记为 $ \operatorname {Out} (G)$。

例 1　不是内自同构的自同构

　　 取复数乘法群 $(\mathbb{C}, \times)$，则取共轭映射 $f(z)=\bar{z}$ 是其上一个自同构，但它显然不是内自同构。由于复数乘法的交换性，复数乘法群上的内自同构只有恒等映射一种。

　　 对于任意群而言，内自同构群的结构是清楚的，由下述定理给出。这个定理其实是群同态基本定理的一个简单应用。

定理 3　

　　 $ \operatorname {Inn}(G)$ 同构于 $G/C(G)$。

　　 证明：

　　 我们只需要给出 $G$ 到 $ \operatorname {Inn}(G)$ 的一个满同态并证明其核为 $C(G)$ 即可。

　　 定义映射 $f:G\to \operatorname {Inn} G$ 为 $f(x)= \operatorname {Ad}_x$，容易知道这是个满射，又因为对任意 $g\in G$,有

\begin{equation} \begin{split} (f(x)f(y))(g)&=( \operatorname {Ad}_x \operatorname {Ad}_y)(g)= \operatorname {Ad}_x(( \operatorname {Ad}_y)(g))\\ &=xygy^{-1}x^{-1}=(xy)g(xy)^{-1}\\ &= \operatorname {Ad}_{xy}(g)\\ &=(f(xy))(g), \end{split}~ \end{equation}
即 $f(x)f(y)=f(xy)$，所以这是一个同态映射。

　　 其核 $\ker(f)=C(G)$，因为若 $x\in\ker(f)$，则对任意 $g\in G$，有 $xgx^{-1}=g$.

　　 所以由习题 2 ，$ \operatorname {Inn}(G)$ 同构于 $G/C(G)$。

　　 证毕。

　　 特别地，由于当 $n\geq 3$ 时 $C(S_n)=\{e\}$，故 $ \operatorname {Inn} S_n$ 与 $S_n$ 同构。

　　 相比内自同构群，自同构群的结构复杂得多。这里单就置换群给出结果。

定理 4　

　　 当 $n\neq 2,6$ 时，置换群 $S_n$ 的自同构群同构于自身。

　　 $S_2$ 的自同构群是平凡群。

　　 $ \operatorname {Out} S_6$ 是 2 阶循环群。

1. ^ 这个词是用词根 “auto（自身的）” 和单词 “isomorphism（同构）” 组合而成的。
2. ^ 这保证了群 $G/\ker(f)$ 存在。
3. ^ 即 $x_1$ 与 $x_2$ 模 $\ker(f)$ 同余，$y_1$ 与 $y_2$ 模 $\ker(f)$ 同余。
4. ^ 需要注意映射的逆和群元的逆的区别，$[f^{-1}(a)]^{-1}=f^{-1}(a^{-1})$。
5. ^ $\pi$ 为自然同态，即若 $N\lhd G,\pi(g)=gN$，易见这是一个满同态。
6. ^ 对任意 $h,h_1,h_2\in H$ 有 $\pi(h)=hN$，$h_1N=h_2N$ 当且仅当 $h_1h_2^{-1}\in H$。因此这实际上是 $H$ 关于 $N$ 的陪集分解 $H/N$。

                     

© 小时科技 保留一切权利