重积分的换序（简明微积分）
贡献者： addis
1以矩形区域的二重定积分为例，什么时候可以交换积分的顺序呢？即
\begin{equation}
\int_{y_1}^{y_2}\int_{x_1}^{x_2} f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} = \int_{x_1}^{x_2}\int_{y_1}^{y_2} f(x, y) \,\mathrm{d}{y} \,\mathrm{d}{x} ~.
\end{equation}
例 1
\begin{equation}
f(x, y) = \frac{x - y}{(x+y)^3}~.
\end{equation}
图 1：式 2 函数曲面图
该函数在 $(0,0)$ 处有一个奇点，即没有定义。但是 $x \in (0, 1]$，$y \in (0, 1]$ 的重积分仍然收敛
\begin{equation}
\int_0^1 \int_0^1 f(x,y) \,\mathrm{d}{x} \,\mathrm{d}{y} = -\frac{1}{2}~,
\qquad
\int_0^1 \int_0^1 f(x,y) \,\mathrm{d}{y} \,\mathrm{d}{x} = \frac{1}{2}~.
\end{equation}
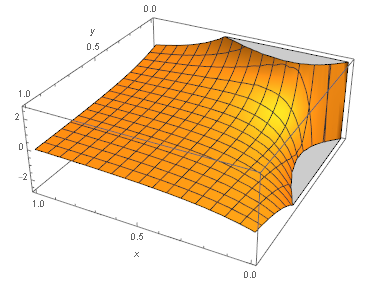
观察图 1 会发现，函数曲面关于积分区域的正方形的对角线 $x=y$ 反对称，也就是对角线的下半三角形的区域中函数值为负，上半三角形函数值为正。且函数在 $x$ 轴和 $y$ 轴靠近原点的地方分别出现了无穷大和无穷小。所以 “曲面下的体积” 是否能取有限值（收敛），取决于无穷大和无穷小是否能在积分过程中抵消。
为了更好理解，我们不妨延正方形的两个对角线方向分别进行积分，即令
\begin{equation}
u = (x+y)/\sqrt{2}~, \qquad
v=(x-y)/\sqrt{2}
\end{equation}
\begin{equation}
g(u,v) = f(x(u,v), y(u,v)) = \frac{v}{2u^3}~.
\end{equation}
所以现在我们看到曲面下方的体积完全取决于我们采用哪两个方向积分。如果积分的过程中刚好可以把正无穷和负无穷实时抵消，那么积分结果就是有限值甚至是零，且值的大小取决于具体抵消的方式。如果上面的坐标旋转变换使用其他角度，还会得到许多其他不同的值。
定理 1 是数学分析中 Fubini 定理的一个特殊应用，Fubini 定理的完整形式和证明超出了本文的范围，将在数学分析中介绍
套用在例 1 中，我们需要看看 $ \left\lvert x-y \right\rvert /(x+y)^3$ 的积分是否是有限的。容易验证积分结果是 $+\infty$，所以并不能保证换序积分结果不变。过程留做习题。