二元函数的极值（简明微积分）

贡献者： addis; ACertainUser

预备知识　导数与函数极值，方向导数

　　¹类似一元函数，二元函数的极值与其偏导数密切相关。以下讨论中，我们假设在某区域内二元函数二阶可导且二阶导数连续。

1. 极值点与驻点

定义 1　二元函数的极值点

　　以一点为圆心在 $xy$ 平面上作一个圆形区域，若当半径足够小时，$f(x_i, y_i)$ 是该圆形区域的最大值或最小值，那么该点就是极大值点或极小值点。

定义 2　驻点

　　如果二元函数 $f(x,y)$ 在某点 $(x_i, y_i)$ 处对 $x, y$ 的偏导数都为零，那么 $(x_i, y_i)$ 就叫做函数 $f(x,y)$ 的驻点。

　　根据式 9 ，驻点处各个方向的方向导数也都为零。

\begin{equation} \frac{\partial f}{\partial x} = \frac{\partial f}{\partial y} =0 \Longleftrightarrow \boldsymbol\nabla f= \boldsymbol{\mathbf{0}} ~. \end{equation}

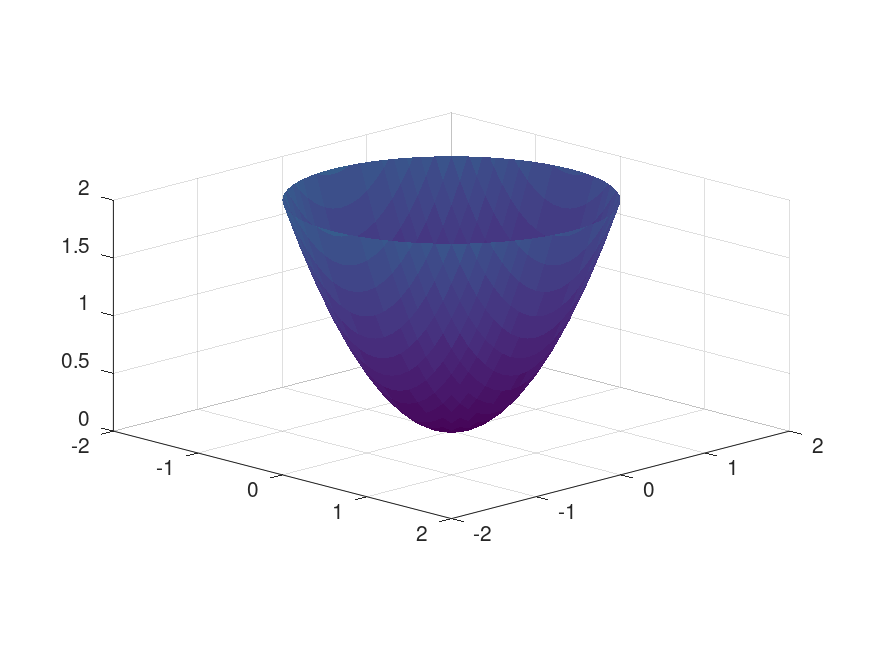
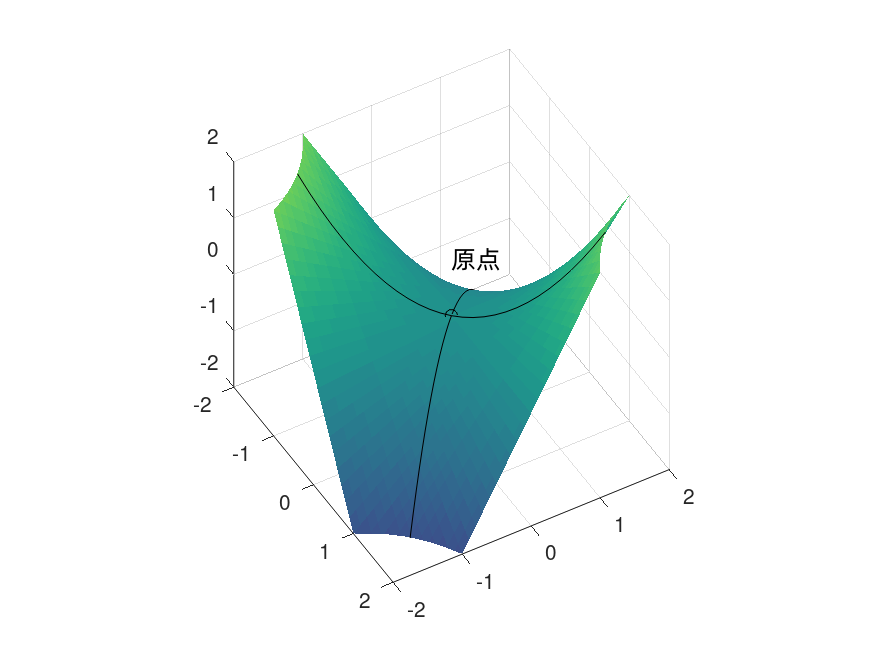
　　与一元函数类似，极值点一定是驻点，但驻点不一定是极值点。例如 $f(x,y) = xy$ 在坐标原点的两个一阶偏导都为零，但原点并不是极值点。

图 1：原点是 $f(x,y)=x^2+y^2$ 的极值点

图 2：但原点不是 $f(x,y)=xy$ 的极值点

2. 极值点判别法（充分非必要条件）

　　在驻点处，设

\begin{equation} A= \frac{\partial^{2}{f}}{\partial{x}^{2}} ,\qquad B= \frac{\partial^2 f}{\partial x \partial y} ,\qquad C= \frac{\partial^{2}{f}}{\partial{y}^{2}} ~. \end{equation}

\begin{equation} D=AC-B^2= \begin{vmatrix} A&B\\ B&C\end{vmatrix} ~. \end{equation}

若 $D<0$, 则该驻点不是极值点
若 $D>0$ 且 $A>0$, 则该驻点为 $f(x,y)$ 的极小值点
若 $D>0$ 且 $A<0$, 则该驻点为 $f(x,y)$ 的极大值点
否则，该点可能是也可能不是极值，不能使用该判别法判定

习题 1　二次函数

　　求以下二次函数的极值

\begin{equation} f(x, y) = ax^2 + 2bxy + cy^2 + px + qy~. \end{equation}

部分答案：存在唯一极小值当且仅当 $a>0$, $c>0$, 且 $ac>b^2$；存在唯一极大值当且仅当 $a<0$, $c<0$, 且 $ac>b^2$。

3. 推导

　　类比一元函数的证明，要证明二元函数的某点是极值点，就要证明该点的任意二阶方向导数都大于零或都小于零²。令某方向为 $ \hat{\boldsymbol{\mathbf{n}}} = \hat{\boldsymbol{\mathbf{x}}} \cos\theta + \hat{\boldsymbol{\mathbf{y}}} \sin\theta$，由式 9 得该方向的方向导数为

\begin{equation} \left(\cos\theta \frac{\partial}{\partial{x}} + \sin\theta \frac{\partial}{\partial{y}} \right) f~, \end{equation}

再次求方向导数得二阶方向导数为

\begin{equation} \left(\cos\theta \frac{\partial}{\partial{x}} + \sin\theta \frac{\partial}{\partial{y}} \right) ^2 f = \frac{\partial^{2}{f}}{\partial{x}^{2}} \cos^2\theta + 2 \frac{\partial^2 f}{\partial x \partial y} \sin\theta\cos\theta + \frac{\partial^{2}{f}}{\partial{y}^{2}} \sin^2\theta~. \end{equation}

如果你还不习惯看算符的平方，可以把上式的括号项平方看做两个括号项，依次作用在函数上。以极小值为例，令上式恒大于零，并除以 $\cos^2\theta$ 得

\begin{equation} \frac{\partial^{2}{f}}{\partial{y}^{2}} \tan^2\theta + 2 \frac{\partial^2 f}{\partial x \partial y} \tan\theta + \frac{\partial^{2}{f}}{\partial{x}^{2}} > 0~. \end{equation}

上式左边是关于 $\tan\theta$ 的二次函数，若要恒大于零，则二次项系数要大于零，且判别式需小于零，立即可得 $AC-B^2>0$。同理可得极大值条件。

　　当判别式（$AC-B^2$）小于零时，必然存在不同方向的二阶方向导数具有相反的符号，所以必定不是极值点。而当判别式等于零时，存在某些方向的二阶导数为零，无法判断是否为极值点。

1. ^ 本文参考： [1] 下册的 “多元函数的极值及其求法” 一节。
2. ^ 否则延一个方向前进函数值会越来越大，而延另一个方向前进函数值会越来越小，这个点就不是极值点

[1] ^ 同济大学数学系. 高等数学 (上下册) 高等教育出版社 (2014) 第七版