能量法解谐振动问题
贡献者： FFjet
由于谐振动系统的总能量是常量，反过来我们可以用机械能守恒定律来导出谐振动的运动方程。仍以弹簧振子为例，在任一时刻，振子作谐振动的总机械能等于势能加上动能，即
\begin{equation}
E=E_{\mathrm k}+E_{\mathrm p}=\frac{1}{2} m v^{2}+\frac{1}{2} k x^{2}~.
\end{equation}
\begin{equation}
m v \frac{\mathrm{d} v}{\mathrm{d} t}+k x \frac{\mathrm{d} x}{\mathrm{d} t}=0~.
\end{equation}
\begin{equation}
\frac{\mathrm{d}^{2} x}{\mathrm{d} t^{2}}+\frac{k}{m} x=0~.
\end{equation}
能量法在解简谐运动（广义来说，机械能守恒的）问题中非常有帮助，下面来看一个例题。
例 1 考虑弹簧质量的弹簧振子
当考虑弹簧的质量时，用能量法求解弹簧振子的周期。设弹簧的质量为 $m_0$，且小于振动物体的质量 $m$，弹簧的劲度系数为 $k$，弹簧的原长为 $L$。
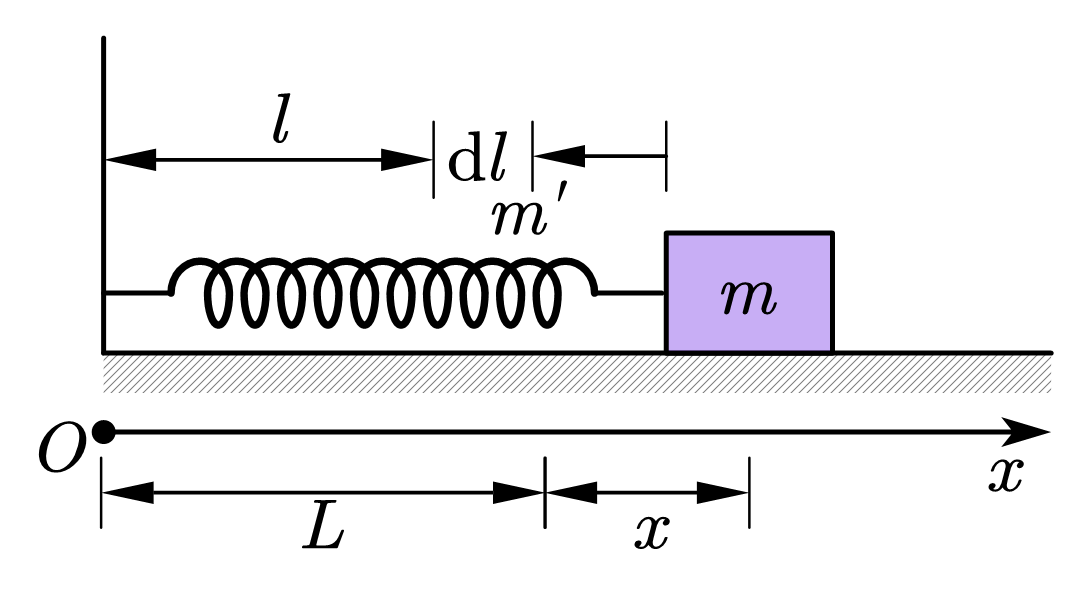
图 1：考虑弹簧质量的弹簧振子
在振动过程中任一时刻，设物体的位移为 $x $，速度为 $v$。如图 1 所示。弹簧振动时，可以认为弹簧在振动的任一时刻内，各等长小段的变形相同，弹簧各截面处的位移是线性变化的。在离弹簧固定端距离 $l$ 的地方取一小段微元长度 $\mathrm dl$，质量即为 $\dfrac{m^\prime}{L}\mathrm{d}l$，位移为 $\dfrac{x}{L}l$，因而该段微元长度的速度就等于 $\dfrac{v}{L}l$，写出其微元动能的表达式：
\begin{equation}
\mathrm{d} E_{\mathrm{k}}^{\prime}=\frac{1}{2}\left(\frac{m^{\prime}}{L} \mathrm{d} l\right)\left(\frac{l}{L} v\right)^{2}=\frac{m^{\prime} v^{2}}{2 L^{3}} l^{2} \mathrm{d} l~.
\end{equation}
\begin{equation}
E_{\mathrm{k}}^{\prime}=\int_{0}^{L} \frac{m^{\prime} v^{2}}{2 L^{3}} l^{2} \mathrm{d} l=\frac{1}{2} \frac{m^{\prime}}{3} v^{2}~.
\end{equation}
\begin{equation}
E=\frac{1}{2} k x^{2}+\frac{1}{2} m v^{2}+\frac{1}{2} \frac{m^{\prime}}{3} v^{2}~.
\end{equation}
\begin{equation}
\frac{1}{2} k x^{2}+\frac{1}{2} m v^{2}+\frac{1}{2} \frac{m^{\prime}}{3} v^{2}=E=\mathrm{constant}~.
\end{equation}
\begin{equation}
\left(m+\frac{m^{\prime}}{3}\right) \frac{\mathrm{d}^{2} x}{\mathrm{d} t^{2}}+k x=0~.
\end{equation}
\begin{equation}
\frac{\mathrm{d}^{2} x}{\mathrm{d} t^{2}}+\omega^{2} x=0~, \qquad \left(\omega^{2}=\frac{k}{m+m^{\prime} / 3} \right) ~.
\end{equation}
\begin{equation}
T=\frac{2 \pi}{\omega}=2 \pi \sqrt{\frac{m+m^{\prime} / 3}{k}}~.
\end{equation}