线性算子的行列式
贡献者: Giacomo
- 本文存在未完成的内容。
1. 体积形式
我们把 $n$ 维向量空间 $V$ 上的反对称 $n$-形式称为体积形式。
当 $\mathbb{F} = \mathbb{R}$ 时,这个定义符合我们的直觉,体积指的是定向平行多胞体的有向体积(signed volume)。
图 1:平行四边性
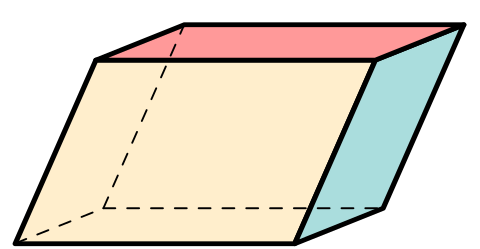
图 2:平行六面体
更一般的,反对称 $k$-形式 $\omega$ 给每个定向平行 $k$-胞体定义了一个有向 $k$ 维体积:
\begin{equation}
\operatorname {vol}_k(P, v_1, \cdots, v_k): = \omega(v_1, \cdots, v_k)~.
\end{equation}
未完成:画图
2. 行列式
$f$ 的 $k$ 阶张量幂 $f^{\otimes k}: V^{\otimes k} \to W^{\otimes k}$ 保留了 $V^{\otimes k}$ 元素的反对称性,
\begin{equation}
\begin{aligned}
f(v_1 \wedge \cdots \wedge v_k) &= \sum_{\sigma \in S_n} \operatorname {sign}(\sigma) f(v_{\sigma(1)}) \otimes \cdots \otimes f(v_{\sigma(k)}) \\
&= f(v_1) \wedge \cdots \wedge f(v_k)~.
\end{aligned}~
\end{equation}
如果 $f$ 是一个线性算子,即 $f: V \to V$,我们发现 $k$ 阶反对称幂子空间 ${\large \wedge}^k V$ 是 $f^{\otimes k}$ 的不变子空间,因此 ${\large \wedge}^k f$ 是 ${\large \wedge}^k V$ 上的线性算子。
特别的记 $V$ 的维度为 $n$,我们有 $\dim({\large \wedge}^n V) = 1$,因此
\begin{equation}
{\large \wedge}^k f: {\large \wedge}^n V \to {\large \wedge}^n V~
\end{equation}
\begin{equation}
({\large \wedge}^k f)(v) = \lambda v~
\end{equation}
未完成:证明 1:线性算子的行列式等于它对应的矩阵的行列式
未完成:证明 2:线性算子的行列式等于体积形式的变化因子
1. ^ 严格来说这时候我们应该记定向平行多胞体为 $(P, v_1, \cdots, v_k)$。