cos2 波包

贡献者： addis

1. cos2 波包

　　 $\cos^2$ 波包也叫 $\sin^2$ 波包，比起高斯波包，它的优点是存在明确的范围。它的函数形式为

\begin{equation} f(x) = \left\{\begin{aligned} &A\cos^2 \left(\frac{\pi x}{L} \right) \mathrm{e} ^{ \mathrm{i} k x} && ( \left\lvert x \right\rvert < L/2)\\ &0 && (\text{otherwise})~. \end{aligned}\right. \end{equation}

其中 $L$ 是波包的总长度。它的 FWHMI 为

\begin{equation} \text{FWHMI} = \frac{2}{\pi} \operatorname {acos}(2^{-1/4}) L \approx 0.3640567 L~. \end{equation}

满足 $f^2(\text{FWHMI/2}) = f^2(0)/2$。

　　积分为（令 $a = \pi/L$）

\begin{equation} \begin{aligned} &\quad \int A\cos^2 \left(a x \right) \mathrm{e} ^{ \mathrm{i} kx} \,\mathrm{d}{x} = - \mathrm{i} \frac{A}{4} \mathrm{e} ^{ \mathrm{i} kx} \left(\frac{2}{k} +\frac{ \mathrm{e} ^{2 \mathrm{i} ax}}{2a+k} -\frac{ \mathrm{e} ^{-2 \mathrm{i} ax}}{2a-k} \right) + \frac{2 \mathrm{i} Aa^2\cos[{\pi k}/{(2a)}]}{k(4 a^2 -k^2)} + C\\ &= \frac{Ax}{4} \left(2 \operatorname{sinc} (k x) + \operatorname{sinc} [(2 a+k)x] + \operatorname{sinc} [(2 a-k)x] \right) \\ &\quad + \mathrm{i} \frac{A}{4} \left(-\frac{2 \cos\left(k x\right) }{k} -\frac{\cos[(2 a+k)x]}{2 a+k} +\frac{\cos[(2 a-k)x]}{2 a-k} \right) + \frac{2 \mathrm{i} Aa^2\cos[{\pi k}/{(2a)}]}{k(4 a^2 -k^2)} + C~. \end{aligned} \end{equation}

$C$ 前面的部分在 $x = \pm\pi/(2a)$ 处分别为 $\frac{\pm 2 Aa^2\sin[{\pi k}/{(2a)}]}{k(4 a^2 -k^2)}$，易得无穷定积分只有实部

\begin{equation}\int_{-\infty}^{+\infty} f(x) \,\mathrm{d}{x} = \int_{-\pi/(2a)}^{\pi/(2a)} A\cos^2 \left(a x \right) \mathrm{e} ^{ \mathrm{i} k x} \,\mathrm{d}{x} = \frac{4 Aa^2\sin[{\pi k}/{(2a)}]}{k(4 a^2 -k^2)}~. \end{equation}

另外，实部是奇函数，虚部是偶函数。

　　傅里叶变换（注意是实数）：

\begin{equation} \tilde f(k) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{+\infty} f(x) \mathrm{e} ^{- \mathrm{i} \omega x} \,\mathrm{d}{x} = \frac{\sqrt{2} \pi ^{3/2} A L}{4 \pi ^2-L^2 (\omega-k)^2} \operatorname{sinc} [L(\omega-k)/2]~. \end{equation}

零点的位置为

\begin{equation} k = k_0 \pm 2n\pi/L \qquad (n=2,3,\dots)~. \end{equation}

标准差约为 $2.92544/L$，方差 $13.15947/L^2$，FWHMI $9.05144/L$。

　　画图对比如下（代码见文末）：

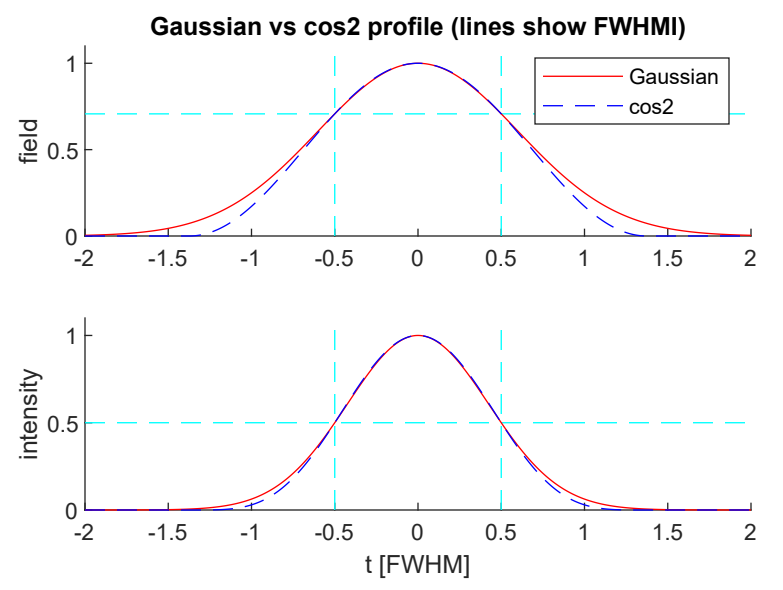
图 1：高斯波包和 cos2 波包的对比

2. 附：Matlab 画图代码

代码 1：cos2_spec.m

% properties of cos2 wave packet spectra

A = 0.9; L = 1.12;
g = @(k) (sqrt(2)*pi^1.5*A*L)./(4*pi^2-L^2*k.^2) .* sinc(L*k/2);

k = linspace(-40, 40, 1000);
figure; plot(k, g(k));
grid on;
xlabel k;
hold on;
scatter((2:6)*2*pi/L, 0, 'k');
scatter((-6:-2)*2*pi/L, 0, 'k');
axis([-40, 40, -0.02, 0.21]);

A = 1/sqrt(integral(@(k)g(k).^2, -inf, inf));
integral(@(k)g(k).^2.*abs(k).*A^2, -inf, inf)

代码 2：FWHMIsin2

% FWHMI of wave packets
% FWHMI: full width half maximum intensity
% return the ratio of FWHMI of sin2 (field) wave v.s. total duration
% satisfy: |cos(pi/2 * FWHMIsin2)^2|^2 == 1/2

function ret = FWHMIsin2
    ret = 2*acos(2^(-1/4))/pi;
end

代码 3：cos2_gaussian_compare.m

% plot Gaussian vs cos2 profile

% gaussian
FWHMI = 1;
a = iFWHMIexp(FWHMI);
x = linspace(-2*FWHMI, 2*FWHMI, 1000);
field_gauss = exp(-a.*x.^2);

% cos2
field_cos2  = zeros(size(x));
dur_cos2 = FWHMI / FWHMIsin2;
mark = abs(x) < dur_cos2/2;
field_cos2(mark) = cos((pi/2)*x(mark)/(dur_cos2/2)).^2;

% plot field profile
figure;
subplot(2, 1, 1); hold on;
axis([min(x), max(x), 0, 1.1]);
plot_vert(-FWHMI/2, 'c--');
plot_vert(FWHMI/2, 'c--');
plot_hori(sqrt(1/2), 'c--');
plot(x, field_gauss, 'r');
plot(x, field_cos2, 'b--');
legend({'', '', '', 'Gaussian', 'cos2'});
% xlabel('t [FWHM]');
ylabel('field');
title('Gaussian vs cos2 profile (lines show FWHMI)');

% plot intensity profile
subplot(2, 1, 2); hold on;
axis([min(x), max(x), 0, 1.1]);
plot_vert(-FWHMI/2, 'c--');
plot_vert(FWHMI/2, 'c--');
plot_hori(1/2, 'c--');
plot(x, field_gauss.^2, 'r');
plot(x, field_cos2.^2, 'b--');
xlabel('t [FWHM]');
ylabel('intensity');

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。