浙江大学 2012 年硕士入学量子力学考试试题
贡献者: 待更新
声明:“该内容来源于网络公开资料,不保证真实性,如有侵权请联系管理员”
1. 简答题
第一题
- 证明厄米算符的本征值为实数
- 对于力 $ \hat{\boldsymbol{\mathbf{H}}} =\frac{ \hat{\boldsymbol{\mathbf{p}}} ^2}{2m}+\alpha \hat{\boldsymbol{\mathbf{L}}} _x$( $\alpha$ 为常数),下列力学量中哪些是守恒量?
$ \hat{\boldsymbol{\mathbf{H}}} , \hat{\boldsymbol{\mathbf{p}}} _x, \hat{\boldsymbol{\mathbf{p}}} _y, \hat{\boldsymbol{\mathbf{p}}} _z, \hat{\boldsymbol{\mathbf{p}}} ^2, \hat{\boldsymbol{\mathbf{L}}} _x, \hat{\boldsymbol{\mathbf{L}}} _y, \hat{\boldsymbol{\mathbf{L}}} _z, \hat{\boldsymbol{\mathbf{L}}} ^2$。 - 原子的受激辐射和自发辐射区别在哪里?
- 你知道哪些纯量子效应?
- 写出泡利矩阵 $\sigma^x= \begin{pmatrix}0&1\\1&0\end{pmatrix} \qquad \sigma^y= \begin{pmatrix}0&-i\\i&0\end{pmatrix} \qquad \theta^z= \begin{pmatrix}1&0\\0&-1\end{pmatrix} $ 满足的对易关系。
第二题
电子被束缚在简谐振子势场 $v=\frac{1}{2}m\omega^2x^2$ 中,若引入 $\displaystyle \hat{\boldsymbol{\mathbf{a}}} =\frac{1}{\sqrt{2}}(\frac{x}{x_0}+\frac{i \hat{\boldsymbol{\mathbf{p}}} }{x_0m\omega}), \hat{\boldsymbol{\mathbf{a}}} ^+ =\frac{1}{\sqrt{2}}(\frac{x}{x_0}-\frac{i \hat{\boldsymbol{\mathbf{p}}} }{x_0m\omega}),x_0=\sqrt{h/m\omega}$,则有 $\displaystyle H=h\omega( \hat{\boldsymbol{\mathbf{a}}} ^+ \hat{\boldsymbol{\mathbf{a}}} +\frac{1}{2})$,并有关系 $ \hat{\boldsymbol{\mathbf{a}}} ^+ \left\lvert n \right\rangle =\sqrt{n+1} \left\lvert n+1 \right\rangle , \hat{\boldsymbol{\mathbf{a}}} \left\lvert n \right\rangle =\sqrt{n} \left\lvert n-1 \right\rangle $,显然基态应满足 $ \hat{\boldsymbol{\mathbf{a}}} \left\lvert 0 \right\rangle =0$。
(1)试求基态波函数。
(2)进一步求第一激发态的波函数。
(3)如果势阱中有两个电子(忽略它们间的相互作用,它们整体的基态波函数是什么?(提示:电子为自旋 1/2 的全同粒子)。
(4)如果加入均匀磁场 B,问当 B 很强,超过某临界 $B_c$ 时,(3)中所述基态还会是基态吗?试具体求 $B_c$
第三题
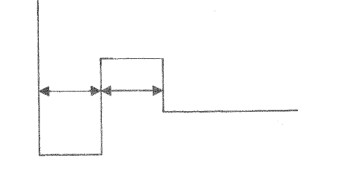
有一个质量为 m 的粒子处在如下势阱中
(1)试求其能级与波函数。
(2)问通过调节势阱宽度 a,能否让阱中的粒子有一定的几率穿透出来。
第四题
将质子看作是半径为 R 的带电球壳,$V(r)= \left\{\begin{aligned} \frac{e}{R}\quad r< R\\\frac{e}{r}\quad r>R \end{aligned}\right. $(其中 e 为基本电荷值,$a_0$ 为玻尔半径,R <<$a_0$),计算由于质子(即氢原子核)的非点性引起氢原子基态能级的一级修正。
第五题
求哈密顿量 $H=\sigma_1^x\sigma_2^x+\sigma_1^y\sigma_2^y+\alpha \sigma_1^z\sigma^x_2$ 的本征值和本征矢量,试分析 $a =1$ 时有何特点。[提示:泡利矩阵的下标 1,2 表示第一个粒子和第二个粒子,因此可用矩阵直乘理解,即 $\sigma_1^x\sigma_2^x=\sigma_1^x \otimes \sigma_2^x$ 等等]
第六题
有一个量子系统,假如你已知道基态和激发态的波函数分别是 $\varphi_0,\varphi_1,\varphi_2,\varphi_3$ 对应于 $E_0< E_1< E_2< E_3 \dots$,把两个全同粒子(不考虑它们之间的相互作用)放到该系统,
(1)对于自旋为零的粒子,写出基态与第一激发态的波函数。
(2)对于自旋为 1/2 的粒子,写出基态波函数。
友情链接: 超理论坛 | ©小时科技 保留一切权利