雅各布·伯努利（Jacob Bernoulli）（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图
图 1

　　 雅各布·伯努利 \(^\text{[a]}\)（Jacob Bernoulli，也被称为英语中的詹姆斯或法语中的雅克；1655 年 1 月 6 日［旧历 1654 年 12 月 27 日］—1705 年 8 月 16 日）是一位瑞士数学家。在莱布尼茨与牛顿的微积分优先权之争中，他站在戈特弗里德·威廉·莱布尼茨一方，是莱布尼茨微积分法的早期支持者，并为其作出了诸多贡献。作为伯努利家族的一员，他与其兄约翰·伯努利一道，是变分法的奠基人之一。他还发现了基本数学常数 $e$。然而，他最重要的贡献是在概率论领域，在其著作《概率艺术》中首次推导出了大数法则的初步形式。

1. 生平简介

图
图 2：来自《学者通报》（1682 年）的插图，其中刊登了对伯努利《新彗星系统尝试》的批评。

　　 雅各布·伯努利出生于瑞士联邦的巴塞尔，父系是新教香料商人世家，\(^\text{[4][5]}\) 母亲则出身于一个从事银行业与城市治理的家庭。\(^\text{[6]}\)

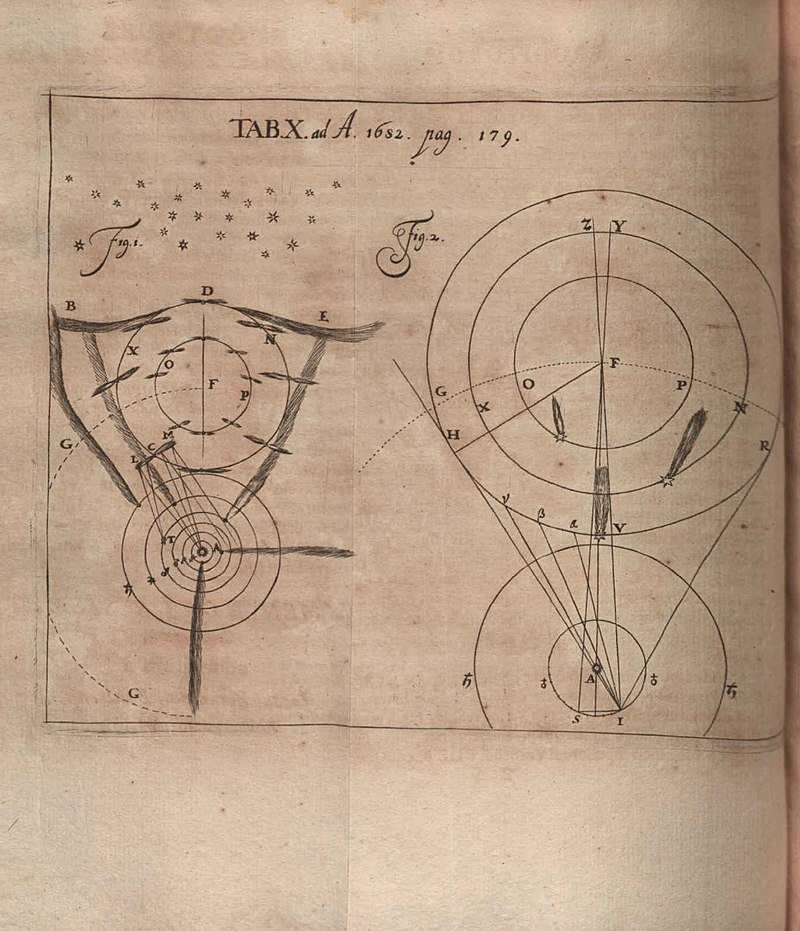
　　 遵从父亲的意愿，他最初学习神学并成为牧师。但与父母的期望相反，\(^\text{[7]}\) 他也私下研习数学和天文学。1676 年至 1682 年间，他游历欧洲各地，向当时的著名学者学习最新的数学与科学成果，其中包括约翰内斯·胡德、罗伯特·波义耳以及罗伯特·胡克的研究。在此期间，他还提出了一种关于彗星的理论，但该理论被证明是错误的。下图为 1682 年《学者通报》刊登的对伯努利彗星新体系尝试的批评：

　　 伯努利返回瑞士后，自 1683 年起在巴塞尔大学教授力学。他的博士论文《三重问题的解法》完成于 1684 年，\(^\text{[8]}\) 并于 1687 年正式出版。\(^\text{[9]}\)

　　 1684 年，雅各布·伯努利与朱迪思·斯图帕努斯结婚，育有两名子女。在这一时期，他也开始了卓有成效的研究生涯。旅行使他得以与当时许多杰出的数学家和科学家建立通信联系，并保持终生往来。在此期间，他深入研究了数学领域的新发现，包括惠更斯的《论掷骰游戏中的推理》、笛卡尔的《几何学》以及范·斯霍滕为其所作的补编。他还研读了巴罗与沃利斯的著作，这激发了他对无穷小几何的浓厚兴趣。在 1684 年至 1689 年之间，他也发现了许多后来构成《概率艺术》的核心成果。

　　 据认为，伯努利于 1687 年被任命为巴塞尔大学数学教授，并在该职位上一直工作到去世。此时，他已经开始指导其弟约翰·伯努利学习数学。他们兄弟俩共同研读了莱布尼茨在 1684 年发表于《学者通报》的论文《极大极小值新方法》中提出的微积分理论。他们还学习了齐恩豪斯的著作。需要指出的是，莱布尼茨早期发表的微积分论文对当时的数学家来说十分晦涩难懂，而伯努利兄弟是最早尝试理解并应用莱布尼茨理论的人之一。

　　 雅各布曾与弟弟在微积分的诸多应用上合作，但随着约翰的数学才能日益成熟，两人之间的合作逐渐演变为激烈的竞争。他们不仅在著作中互相抨击，还频繁地互相出难题来考验对方的技巧。\(^\text{[10]}\) 到了 1697 年，兄弟关系已彻底破裂。

　　 月球上的伯努利环形山即是以两兄弟的名字共同命名的。

2. 重要著作

　　 雅各布·伯努利的第一批重要贡献包括：1685 年发表的一篇关于逻辑与代数对比的小册子，1685 年关于概率的研究，以及 1687 年的几何研究。他的几何成果提出了一种通过两条垂线将任意三角形分成四个相等部分的构造方法。

　　 到 1689 年，他已发表了关于无穷级数的重要研究，并在概率论中提出了大数法则。1682 年至 1704 年间，伯努利共发表了五篇关于无穷级数的论文。其中前两篇包含了许多结果，例如基本结论 $\sum \frac{1}{n}$ 发散，伯努利认为这是他的新发现，实际上意大利数学家彼得罗·门戈利早在 40 年前就已证明，而尼科尔·奥雷斯姆更是在 14 世纪就已得出这一结论 \(^\text{[11]}\)。伯努利无法求出 $\sum \frac{1}{n^2}$ 的闭式解，但他证明了该级数收敛于小于 2 的某个有限值。后来由欧拉在 1737 年首次求出了该级数的确切极限。伯努利还研究了由复利计算引出的指数级数。

　　 1690 年 5 月，伯努利在《学者通报》发表论文指出，等时线问题等价于求解一个一阶非线性微分方程。等时线，也称恒时降线，是指一粒子在重力作用下，无论从曲线上的哪个点出发，都会在相同时间内到达最低点的那条曲线。该问题曾在 1687 年由惠更斯研究过，1689 年又被莱布尼茨研究。在建立了这个微分方程后，伯努利利用我们现在称为 “变量分离法” 的方法对其进行了解。他在 1690 年的这篇论文对于微积分史具有重要意义，因为 “积分” 一词首次以 “求积分” 的含义被使用。1696 年，伯努利求解了现今称为 “伯努利微分方程” 的： $$ y' = p(x)y + q(x)y^n.~ $$ 伯努利还发现了一种确定一条曲线的渐屈线的一般方法，即作为其曲率圆包络的方法。他还研究了焦线，特别研究了抛物线、对数螺线和本轮线所对应的焦线，时间大约在 1692 年左右。伯努利八字线是雅各布·伯努利于 1694 年首次构想出来的。在 1695 年，他研究了吊桥问题，即：设计一条曲线，使得沿缆绳滑动的重物始终能保持吊桥处于平衡状态。

图
图 3：《概率艺术》，1713 年出版（米兰，曼苏蒂基金会藏）。

　　 伯努利最具原创性的著作是《概率艺术》，该书于他去世八年后的 1713 年在巴塞尔出版。这部作品在他去世时尚未完成，但在概率论的发展史上仍具有极其重要的地位。书中还涉及了其他相关主题，包括对组合数学的回顾，特别是对范·斯胡滕、莱布尼茨和普雷斯泰等人工作的评述；以及在指数级数的讨论中对伯努利数的运用。受惠更斯作品的启发，伯努利还给出了许多关于在各种赌博游戏中可以期望赢得多少的实例。“伯努利试验” 这一术语正是源自该书。

　　 在书的最后部分，伯努利概述了许多数学概率的研究领域，包括：概率作为确定性的可度量程度；必然与偶然；道德期望与数学期望之区别；先验概率与后验概率；按技巧水平划分玩家时的胜利期望；如何考虑所有可得论据、评估其价值并进行可计算的推理；以及大数法则。

　　 伯努利是形式化高等分析方法最重要的倡导者之一。他在表达和行文中虽少有华丽与优雅，但其方法却展现了极高的严谨性与诚实精神。

3. 数学常数 e 的发现

　　 1683 年，雅各布·伯努利在研究一个关于复利的问题时发现了常数 e。他需要求解如下表达式的极限值（该值实际上就是 e）：\(^\text{[12][13]}\) $$ \lim_{n \to \infty} \left(1 + \frac{1}{n} \right)^n~ $$

　　 例如，假设一个账户初始金额为 1 美元，年利率为 100%。如果利息在年末结算一次，最终金额为 2 美元；但如果一年结算两次，则本金每次乘以 1.5，得到： $\$1.00 \times 1.5^2 = \$2.25$ 按季度结算则为： $\$1.00 \times 1.25^4 = \$2.4414\ldots$ 按月结算为： $\$1.00 \times (1.0833\ldots)^{12} = \$2.613035\ldots$

　　 伯努利注意到，随着复利结算间隔越来越短，这个数列趋近于一个极限值（即利率的 “作用力”）。按周复利时金额为 \$2.692597…，按日复利时为 \$2.714567…，仅多出两分钱。设每年复利 n 次，每次利率为 100%/n，则当 n 趋近无穷时，该表达式的极限即为后来欧拉命名为 e 的数值。使用连续复利时，账户金额将达到 \$2.7182818\ldots\$。更一般地说，若账户初始为 1 美元，利率为 R，则连续复利下最终金额为：$e^R$

4. 墓碑

图
图 4：雅各布·伯努利在巴塞尔大教堂的墓碑

　　 伯努利希望在他的墓碑上刻上对数螺线和座右铭 “Eadem mutata resurgo”（“尽管改变，我仍如初重生”）。他写道，这种自相似的螺线 “可以作为一种象征，要么象征逆境中的坚韧与坚定，要么象征人的身体，即使经历所有变化，甚至死亡之后，仍将复归原初与完美之形”。伯努利于 1705 年去世，但墓碑上刻的却是阿基米德螺线而非对数螺线 \(^\text{[14]}\)。

　　 拉丁铭文翻译如下：

　　 雅各布·伯努利，无与伦比的数学家。
巴塞尔大学教授逾十八载；
巴黎与柏林皇家科学院院士；著述等身，享誉盛名。
于身患顽疾中，神志清明至终；
在恩典之年 1705 年 8 月 16 日辞世，享年五十岁七个月，静待复活之日。
茱蒂丝·斯图帕努斯，
与其共度二十载婚姻，
与二子一同，为思念至深的丈夫与父亲竖立此碑。

5. 作品

图
图 5：De gravitate aetheris, 1683
图
图 6：《著作集》，第一卷，1744 年

6. 注释

　　 英语发音：/bɜːrˈnuːli/，读作 “bur-NOO-lee”；瑞士标准德语发音：[ˈjaːkɔb bɛrˈnʊli]。

7. 参考文献

  1. Wells, John C. (2008). 《朗文发音词典》（第 3 版）。朗文出版公司。ISBN 978-1-4058-8118-0。
  2. Mangold, Max (1990). 《杜登——发音词典》第 3 版。曼海姆/维也纳/苏黎世：杜登出版社。
  3. Jacob（Jacques）Bernoulli，《数学史麦克图档案》，英国圣安德鲁斯大学数学与统计学院。
  4. Sensenbaugh, Robert（2013 年 9 月 13 日）。“伯努利家族”，收录于 Frank N. Magill 主编，《17 和 18 世纪：世界人物传记词典》第 4 卷。牛津郡：Routledge，第 122 页。ISBN 978-1135924140。
  5. Peiffer, Jeanne（2006 年 6 月）。“雅各布·伯努利——其弟约翰的导师与对手”（PDF），《概率与统计史电子期刊》，2(1): 3。
  6. Suzuki, J. (2007). Hockey T 等主编，《天文学家传记百科全书》。纽约：Springer 出版社。doi:10.1007/978-0-387-30400-7_141。ISBN 978-0-387-30400-7。2025 年 3 月 1 日通过 Qwant 检索。
  7. Nagel, Fritz（2004 年 6 月 11 日）。“伯努利，雅各布”，《瑞士历史词典》。检索于 2016 年 5 月 20 日。
  8. Kruit, Pieter C. van der（2019）。《扬·亨德里克·奥尔特：银河系系统的大师》，Springer 出版社，第 639 页。ISBN 978-3-030-17801-7。
  9. Bernoulli, Jakob（2006）。《雅各布·伯努利著作集：第 2 卷：基础数学》（意大利语）。Springer 科学与商业传媒，第 92 页。ISBN 978-3-7643-1891-8。
  10. Pfeiffer, Jeanne（2006 年 11 月）。“雅各布·伯努利”（PDF），《概率与统计史电子期刊》。检索于 2016 年 5 月 20 日。
  11. D. J. Struik（1986）《数学原典集（1200–1800）》，第 320 页。
  12. Jacob Bernoulli（1690）《关于利息的一些问题，以及关于博弈概率的解答，发表于 1685 年法国《学者年鉴》》。《学者年鉴》，第 219–223 页。在第 222 页，伯努利提出了复利问题并构造幂级数解答，进而推出 e 的估值范围为 2.5 < e < 3。
  13. J. J. O'Connor；E. F. Robertson，《常数 e》，圣安德鲁斯大学。检索于 2016 年 11 月 2 日。
  14. Livio, Mario（2003）[2002]。《黄金比例：Φ这个令人惊叹的数字的故事》（平装版首版）。纽约：Broadway 图书公司，第 116–117 页。ISBN 0-7679-0816-3。

8. 延伸阅读

9. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利