中国科技大学 2016 年考研普通物理

贡献者： Entanglement

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 简答/选择题（每题 15 分，共 30 分）

1. 设玻尔兹曼常数为 $k$，一理想双原子分子气体，处于温度 $T$ 时，其分子平均能量是多少？
2. 以下哪些电场可以存在于没有电荷的局部空间内？$A$ 是常数，$i$ , $j$ , $k$ 分别是直角坐标系 $x$，$y$，$z$ 方向的单位矢量。请选择所有合适的答案。
   A. $A$(2xyi-xzk) B. $A$(-xyj+xzk) C. $A$(xzi+xzj) D. $A$xyz(i+j)

2. 计算题（每题 20 分，共 120 分）

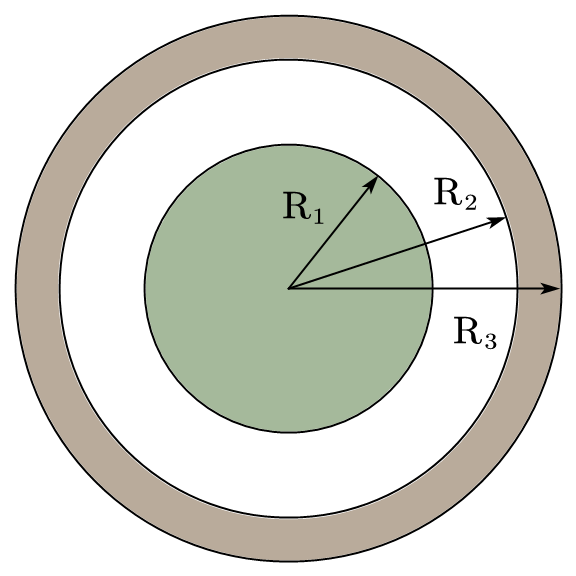
1. 如图 1 所示，半径为 $R_1$ 的导体球外有同心的导体球壳，壳的内外半径分别为 $R_2$ 和 $R_3$。已知球壳带的电量为 $Q$ ,内球和无穷远处电势为 0,求内球的电荷量和球壳的电势。
   
   
   图 1：计算题 1 图示
2. 半径为 $R$ 的球面上均匀分布电荷 $q$ ,该球面以角速度 $\omega$ 绕它的直径旋转。求这个系统的磁矩。
3. 一水桶中装有足够多的水。让该水桶以一定的角速度 $\omega$ 绕其对称轴在水平面内稳定旋转，试定量计算水面的形状。重力加速度为 $g$ ,结论用以转轴为 $z$ 轴的柱坐标系表达。
4. 你双手拿着一面积足够大的平板迎着一喷射的水柱，水柱的流量为 $0.1m^{3}/s$ ,水流的速度为 $5m/s$。
   (1)求平板静止时你给平板的力；
   (2)如果你拿着平板以 $1m/s$ 的速度迎着喷射的水柱移动，该力为多大？假设水的密度为 $1000kg/m^{3}$ .
5. 一摩尔范德瓦尔斯状态方程的气体，如果它的内能由式 $u=cT-a/V$ ( $V$ 为摩尔体积，$a$ 为状态方程常数之一，$c$ 为常数)给出，计算气体的摩尔比热容 $c_v$ 和 $c_p$ .
6. 设某理想气体的绝热指数 $\gamma =c_p/c_v$ 为温度 $T$ 的函数。
   (1)证明在准静态绝热过程中，气体的 T 和 V 满足函数关系 $F(T)V=C$ ,式中 $C$ 为常数，函数 $F(T)$ 的表达式为：
   $\ln F(T)=\int \frac{dT}{(\gamma-1)T}$ .
   (2)利用(1)的结果，证明该气体的可逆卡诺循环的效率仍为：
   $\eta =1-\frac{T_2}{T_1}$