中国科学院大学 2017 年考研 量子力学

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

　　 一、已知一粒子处于一维无限深势阱时，势函数为 $$V = \begin{cases} 0 & 0 < x < a \\\\+\infty & x < 0, x > a \end{cases}~$$ 能量本征函数数为 $\psi_n = \sqrt{\frac{2}{a}} \sin \frac{n\pi x}{a}$，$t = 0$ 时 $\psi(x, 0) = A x (a - x)$。

　　 (1) 求归一化系数 $A$

　　 (2) 求出 $t > 0$ 时的波函数 $\psi(x, t)$

　　 (3) 该粒子处于基态和第一激发态的概率

　　 (4) $t > 0$ 时，粒子坐标的平均值 $x$.

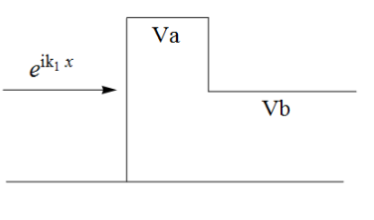
　　 二、如图，已知入射波函数为 $e^{ik_1x}$。

　　 (1) 求入射粒子的流密度

　　 (2) 当 $E = V_b$ 时，透射系数的取值为( )
A 0
B $0 < T < 1$
C 1

　　 (3) 为了怎发透射系数，可以采取的办法有( )
A 保持 $E = V_b$，降低 Va，但保证 $V_a > V_b$
B 在满足 $V_a > V_b$ 的条件下，使 $E > V_b$
C 保持 $E = V_b$，降低 Va,保证 $V_a < V_b$

　　 (4) 若已知入射波函数数为 $ e^{ik_1x}$，反射波函数数为 $R e^{ik_1x}$，透射波函数数为 $S e^{ik_2x}$，其中 $k_1^2 = \frac{2mE}{h^2}, k_2^2 = \frac{2m(E - V_b)}{h^2} $，透射系数为（）
A. $|S|^2$
B. $1 - |R|^2$
C. 以上都不是

　　 　　 三、 (1) 证明量子体系满足 Ehrenfest 定理： $$\begin{cases}\frac{d \overline{x} }{dt} = \frac{\overline p }{m} \\\\ \frac{d\overline p }{dt} = -\left\langle \frac{\overline{\partial V}}{\partial x} \right\rangle\end{cases}~$$

　　 (2) 已知二维谐振子处于均匀电场 $(\epsilon_x, \epsilon_y)$ 中，体系的 Hamilton 为 $H = \frac{p_x^2}{2m} + \frac{p_y^2}{2m} + \frac{1}{2}m\omega^2 x^2 + \frac{1}{2}m\omega^2 y^2 - q\epsilon_x x - q\epsilon_y y$ 当电场为 0 时求体系的能级

　　 (3) 以 $q$ 为参量利用 $HF$ 定理求在电场下的能级

　　 　　 四、 已知二体系统哈密顿为 $H = H_0 + \lambda H'$ 其中 $H_0 = \begin{pmatrix}E_1 & 0 \\\\0 & E_2\end{pmatrix}, \quad H' = \begin{pmatrix}0 & ia \\\\-ia & 0\end{pmatrix},$ 且 $\left|\frac{\lambda a}{E_2 - E_1}\right| \ll 1$.
(1) 求能级的二级近似和波函数的一级近似
(2) 求出准确的的能级表达式并和上问进行比较

　　 　　 五、 已知晶格中两局域电子构成的体系： $H = S_x^{(1)} s_x^{(2)} + S_y^{(1)} s_y^{(2)}$

　　 (1) 若 $S = s^{(1)} + s^{(2)}$，$S_z = s_z^{(1)} + s_z^{(2)}$，求 $S^2$ 和 $S_z$ 的本征值

　　 (2) 用 $S$ 和 $S_z$ 表示 $H$

　　 (3) 求该体系哈密顿的能量本征值

　　 (4) 若外加一 $z$ 方向的磁场 $B$，求体系的能级