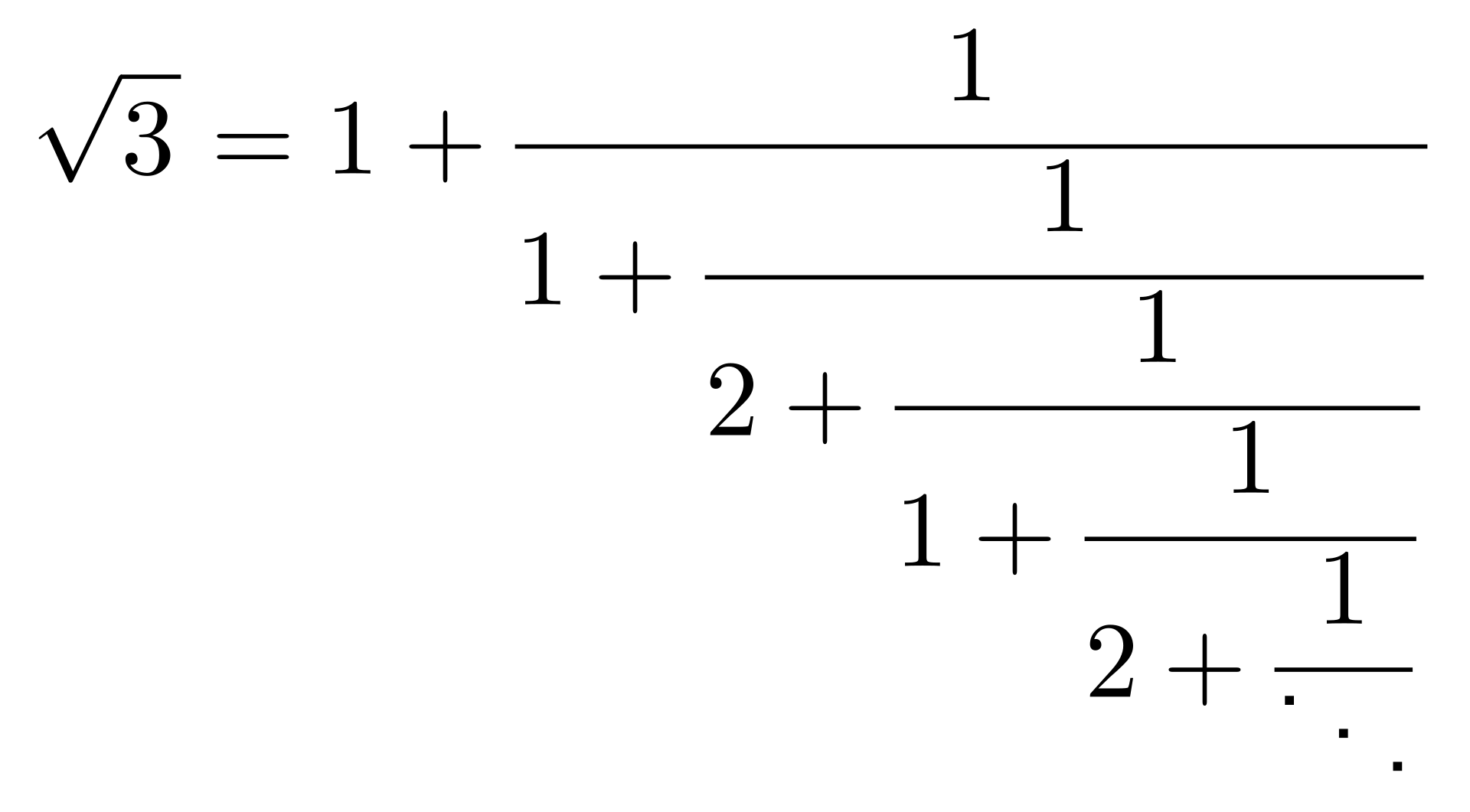数论（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

图
图 1：素数的分布是数论研究的核心问题之一，其在乌拉姆螺旋中的示意图如图所示。该图展示了“素数性”与“取某些二次多项式的值”之间的条件独立性。

　　 数论是纯数学的一个分支，主要致力于研究整数以及算术函数。数论学家研究素数，以及由整数构造的数学对象（例如有理数）的性质，或作为整数的推广而定义的对象（例如代数整数）。

　　 整数既可以单独研究，也可以作为某些方程的解来研究（丢番图几何）。数论中的问题常常能够通过研究某些解析对象来理解，例如黎曼 $\zeta$ 函数，它以某种方式编码了整数、素数或其他数论对象的性质（解析数论）。另外，还可以研究实数与有理数之间的关系，例如研究无理数如何用分数来逼近（丢番图逼近）。

　　 数论与几何一样，是数学最古老的分支之一。数论的一个特点是，它处理的往往是非常容易理解却极难解决的命题。例如，费马大定理在最初提出后的 358 年才被证明，而哥德巴赫猜想自 18 世纪提出以来至今仍未解决。德国数学家卡尔·弗里德里希·高斯曾经说过：“数学是科学的女王，而数论是数学的女王。”\(^\text{[1]}\) 数论一度被视为纯粹数学的典范，认为它在数学之外没有任何应用，直到 20 世纪 70 年代，人们才发现素数可被用作构建公钥密码算法的基础。

1. 历史

　　 数论是数学的一个分支，研究整数及其性质与关系。\(^\text{[2]}\) 整数是一个集合，它在自然数集合 ${1,2,3,\dots}$ 的基础上扩展，加入了数 0，以及自然数的相反数 ${-1,-2,-3,\dots}$。数论学家不仅研究素数，还研究由整数构造的数学对象（例如有理数）的性质，或定义为整数推广的对象（例如代数整数）。\(^\text{[3][4]}\)

　　 数论与算术密切相关，一些作者甚至将这两个词视为同义词。\(^\text{[5]}\) 然而，今天 “算术” 一词通常指研究数值运算的学科，并扩展到实数范围。\(^\text{[6]}\) 在更具体的意义上，数论仅限于研究整数，关注它们的性质和相互关系。\(^\text{[7]}\) 传统上，它也被称为高等算术。\(^\text{[8]}\) 到 20 世纪初，“数论” 这一术语已被广泛采用。\(^\text{[note 1]}\) 其中 “number” 意为整数，既可以指自然数，也可以指全体整数。\(^\text{[9][10][11]}\)

　　 初等数论研究整数的一些方面，这些方面可以用初等方法来探讨，例如利用初等证明。\(^\text{[12]}\) 相比之下，解析数论依赖于复数以及来自分析学和微积分的技巧。\(^\text{[13]}\) 代数数论则使用代数结构（如域和环）来研究数的性质及其相互关系。几何数论运用几何学的概念研究数。\(^\text{[14]}\) 数论的其他分支还包括：概率数论 \(^\text{[15]}\)、组合数论 \(^\text{[16]}\)、计算数论 \(^\text{[17]}\)，以及应用数论，后者研究数论在科学与技术中的应用。\(^\text{[18]}\)

起源

图
图 2：普林普顿 322 泥板文书

　　 在有记录的历史中，数的知识存在于古代的美索不达米亚、埃及、中国和印度文明中 \(^\text{[19]}\)。已知最早的算术性质的历史发现是普林普顿 322 号泥板，约公元前 1800 年。它是一块破碎的泥板，包含了一张毕达哥拉斯三元组（即整数 $(a,b,c)$，满足 $a^{2}+b^{2}=c^{2}$ 的数对）的列表。这些三元组数量众多且数值很大，不可能通过蛮力枚举得到 \(^\text{[20]}\)。

　　 该表的布局表明，它是借助于在现代语言中可写作如下的恒等式构造出来的 \(^\text{[21]}\)： $$ \left(\tfrac{1}{2}\left(x-\tfrac{1}{x}\right)\right)^{2}+1 =\left(\tfrac{1}{2}\left(x+\tfrac{1}{x}\right)\right)^{2},~ $$ 这一恒等式隐含在古巴比伦日常的习题中 \(^\text{[22]}\)。不过也有人提出，该表可能是作为学校习题的数值例子的来源 \(^\text{[23][note 2]}\)。普林普顿 322 泥板是巴比伦数学中唯一现存的证据，可以被视为与现代所谓数论相对应的成果；然而，当时的一种巴比伦代数学要发达得多 \(^\text{[24]}\)。

　　 尽管其他文明可能在最初对希腊数学有所影响 \(^\text{[25]}\)，但所有关于这种借鉴的证据都出现得相对较晚 \(^\text{[26][27]}\)，因此很可能希腊的 arithmētikḗ（数的理论性或哲学性研究）是一种本土传统 \(^\text{[28]}\)。古希腊人对整除性产生了浓厚兴趣。毕达哥拉斯学派赋予完全数与亲和数神秘的性质。毕达哥拉斯的传统还谈及所谓的多边形数或图形数 \(^\text{[29]}\)。欧几里得在其《几何原本》中专门论述了一些属于初等数论的主题，包括素数与整除性 \(^\text{[30]}\)。他提出了用于计算两个数的最大公约数的欧几里得算法，并给出了一个证明，表明素数的数量是无限的。晚期古代最重要的 arithmētikḗ权威是亚历山大的丢番图，他大约生活在公元三世纪。他撰写了《算术》，这是一部题集，其中的问题无一例外是寻找某个多项式方程组的有理数解，通常形式为：$f(x,y) = z^{2}$ 或 $f(x,y,z) = w^{2}$.用现代术语来说，丢番图方程是指要求有理数或整数解的多项式方程。

图
图 3：丢番图《算术》拉丁文译本（1621 年，巴谢译）的书名页。

　　 在罗马帝国灭亡之后，数论的发展转向亚洲，尽管过程断断续续。中国剩余定理出现在《孙子算经》（约三至五世纪）的一道习题中 \(^\text{[31][32]}\)。这一结果后来被推广，并在秦九韶 1247 年的《数学九章》中以完整解法 “大衍术” 呈现 \(^\text{[33][34]}\)。中国数学中也存在某些数秘学思想 \(^\text{[note 3]}\)，但与毕达哥拉斯学派不同，这些思想似乎并未带来实质性的数学进展。尽管希腊天文学可能影响了印度的学术 \(^\text{[35]}\)，但印度数学在其他方面似乎是一种本土传统 \(^\text{[36][37]}\)。阿耶波多（Āryabhaṭa, 476–550 AD）提出，同时同余式对 $n \equiv a_{1} \pmod{m_{1}}, \quad n \equiv a_{2} \pmod{m_{2}}$ 可以通过一种他称为 kuṭṭaka（意为 “粉碎法” 或 “逐次约化法”）的算法来求解【38】；这一过程与欧几里得算法十分接近 \(^\text{[39]}\)。阿耶波多似乎主要考虑其在天文计算中的应用 \(^\text{[35]}\)。婆罗摩笈多（Brahmagupta, 公元 628 年）则开启了对不定二次方程的系统研究，尤其是 Pell 方程。一种通解 Pell 方程的方法可能最早由 Jayadeva 发现；而最早保存下来的系统论述，则见于 Bhāskara II（婆什迦罗二世）十二世纪的《种数论》\(^\text{[40]}\)。

图
图 4：西方视野中的伊本·海赛姆：在《月面学》的卷首插图中，‘Alhasen’（即伊本·海赛姆）代表理性之知，而伽利略则代表感官之知。

　　 九世纪初，哈里发马蒙下令翻译大量希腊数学著作，以及至少一部梵文著作 \(^\text{[41][42]}\)。丢番图的主要著作《算术》由古斯塔·伊本·卢卡（Qusta ibn Luqa, 820–912）译为阿拉伯文。卡拉吉（al-Karajī, 953 – 约 1029）的部分著作《al-Fakhri》在一定程度上以此为基础。据 Rashed Roshdi 所言，卡拉吉的同时代人伊本·海赛姆已经知道后来被称为威尔逊定理的结果 \(^\text{[43]}\)。在中世纪的西欧，除斐波那契所作关于等差数列平方数的论著外，几乎没有真正意义上的数论研究。直到文艺复兴晚期，随着对希腊古代著作的重新研究，这一局面才开始改变。其催化剂是丢番图《算术》的文本校订和译为拉丁文 \(^\text{[44]}\)。

近代早期数论

图
图 5：皮埃尔·德·费马

　　 法国数学家皮埃尔·德·费马（Pierre de Fermat, 1607–1665）从未正式发表过著作，而是通过通信以及在书页空白处的批注来交流思想 \(^\text{[45]}\)。他对数论的贡献重新激发了欧洲对这一领域的兴趣。他提出了费马小定理（模算术中的一个基本结果）、费马大定理，并证明了费马直角三角形定理 \(^\text{[2][46]}\)。他还研究了素数、四平方和定理以及 Pell 方程 \(^\text{[47][48]}\)。莱昂哈德·欧拉（Leonhard Euler, 1707–1783）对数论的兴趣最早可以追溯到 1729 年。当时，他的朋友、业余数学爱好者 \(^\text{[note 4]}\) 克里斯蒂安·哥德巴赫 向他推荐了费马在这一领域的一些工作 \(^\text{[49][50]}\)。在费马未能成功引起同时代学者广泛关注之后，这一事件被称为现代数论的 “再生”\(^\text{[51][52]}\)。欧拉证明了费马的一些断言，包括费马小定理；他率先开展了关于 “每个整数都可以写成四个平方数之和” 的证明工作 \(^\text{[53]}\)；并处理了费马大定理的某些特例 \(^\text{[54]}\)。他还研究了连分数与 Pell 方程之间的联系 \(^\text{[55][56]}\)，并首次迈向了解析数论 \(^\text{[57]}\)。

图
图 6：莱昂哈德·欧拉

　　 三位欧洲同时代的数学家延续了初等数论的研究：约瑟夫–路易·拉格朗日（Joseph-Louis Lagrange, 1736–1813）给出了四平方和定理、威尔逊定理的完整证明，并发展了 Pell 方程的基本理论。阿德里安–玛丽·勒让德（Adrien-Marie Legendre, 1752–1833）提出了二次互反律，并猜想了相当于素数定理和狄利克雷算术级数定理的结果。他还系统研究了方程 $ ax^{2} + by^{2} + cz^{2} = 0$ 在他晚年时，他成为第一个证明费马大定理在 (n=5) 情形成立的人 \(^\text{[59]}\)。卡尔·弗里德里希·高斯（Carl Friedrich Gauss, 1777–1855）在 1801 年撰写了《算术研究》，该书对数论产生了巨大影响，并为整个 19 世纪的研究奠定了议程。他在书中证明了二次互反律 \(^\text{[60]}\)，并发展了二次型理论。他还为同余式引入了一些基本记号，并专门讨论了计算问题，包括素性检验 \(^\text{[61]}\)。此外，他建立了单位根与数论之间的联系 \(^\text{[62]}\)。通过这些工作，可以说高斯已在某种意义上为后来的埃瓦里斯特·伽罗瓦的研究，以及代数数论领域，开辟了道路。

数论的成熟与分支划分

图
图 7：彼得·古斯塔夫·勒热纳·狄利克雷

　　 自 19 世纪早期开始，数论逐渐经历了以下发展：

　　 代数数论可说起始于对互反律与圆分问题的研究，但真正走向成熟则依赖于抽象代数、理想论与赋值论的早期发展（见后文）。解析数论的常规起点是狄利克雷算术级数定理（1837）\(^\text{[64][65]}\)，其证明引入了 L-函数，并涉及一些渐近分析以及对实变量的极限过程 \(^\text{[66]}\)。

　　 实际上，最早在数论中使用解析思想可追溯至欧拉（1730 年代）\(^\text{[67][68]}\)，他使用了形式幂级数以及非严格（或隐含）的极限论证。将复分析引入数论则要更晚一些：黎曼（Bernhard Riemann, 1859）关于 $\zeta$ 函数的研究是公认的起点 \(^\text{[69]}\)。而 雅可比的四平方和定理（1839）虽更早，却属于最初不同的研究方向，如今已在解析数论中占据核心地位（模形式）\(^\text{[70]}\)。

　　 美国数学会设立了柯尔数论奖。此外，数论还是费马奖所奖励的三大数学分支之一。

2. 主要分支

初等数论

图
图 8：数论学家保罗·埃尔德什与陶哲轩于 1985 年的合影，当时埃尔德什 72 岁，陶哲轩 10 岁

　　 初等数论通过算术中的基本方法研究数论中的主题。\(^\text{[4]}\) 它的主要研究对象包括整除性、因式分解和素数性，以及模算术中的同余关系。\(^\text{[71][12]}\) 其他的研究内容还包括丢番图方程、连分数、整数拆分以及丢番图逼近。\(^\text{[72]}\)

　　 算术是研究数值运算的学科，探讨数字如何通过加法、减法、乘法、除法、乘方、开方和对数等算术运算进行组合和变换。例如，乘法是一种运算，它将两个数（称为因子）结合成一个数（称为积），如：$2 \times 3 = 6$\(^\text{[73]}\)。

　　 整除性是两个非零整数之间的一种性质，与除法相关。若一个整数 $a$ 可以被一个非零整数 $b$ 整除，则称 $a$ 是 $b$ 的倍数；换言之，存在某个整数 $q$，使得 $a = bq$。另一种等价的表述是：$b$ 整除 $a$，记作 $b \mid a$。反之，若不满足整除关系，则 $a$ 不能被 $b$ 整除，除法会产生余数。欧几里得的除法引理断言，$a$ 和 $b$ 一般可以表示为：$a = bq + r$,其中余数 $r$ 是最小的正数剩余量。初等数论研究各种整除规则，以便快速判断一个给定整数是否可以被某个固定的除数整除。例如，众所周知，一个整数如果它的十进制各位数字之和能被 3 整除，那么该整数本身也能被 3 整除。\(^\text{[74][9][75]}\)

图
图 9

　　 若若干个非零整数有一个公约数，则该整数能够整除它们所有数。最大的这种约数称为最大公约数（gcd）。如果两个整数的最大公约数是 1，即它们唯一的公约数是 1，则称这两个整数互素或相对素数。欧几里得算法可用于计算两个整数 $a, b$ 的最大公约数，其方法是反复应用除法引理，并在每一步将除数和余数交换位置。该算法还可以扩展来求解线性丢番图方程的特殊情况：$ax + by = 1$。一个丢番图方程一般具有多个未知数，并且系数都是整数。另一类丢番图方程体现在勾股定理中：$x^2 + y^2 = z^2$，如果其解都是整数，则称为勾股三元组。\(^\text{[9][10]}\) 另一种重要的表达形式是连分数，它把一个数写成一个整数与一个分数之和，而分母中的分数又是类似形式的整数与分数之和。\(^\text{[76]}\)

　　 初等数论研究整数的整除性质，例如奇偶性（偶数与奇数）、素数和完全数。一些重要的数论函数包括：约数个数函数、约数求和函数及其变形，以及欧拉函数。素数是指大于 1 的整数，且它的正约数只有 1 和它自身。大于 1 的正整数若不是素数，则称为合数。欧几里得定理证明了素数有无穷多个，即集合 ${2, 3, 5, 7, 11, \dots}$。埃拉托色尼筛法是一种高效算法，它通过逐步剔除所有合数来识别不超过给定自然数的所有素数。\(^\text{[77]}\)

　　 因数分解是一种将一个数表示为乘积的方法。特别是在数论中，整数分解是将一个整数分解为若干整数的乘积。不断重复这一过程直到所有因子都是素数，被称为素因数分解。素数的一个基本性质体现在**欧几里得引理**中。该引理的推论是：如果一个素数能整除若干整数的乘积，那么它必然能整除其中至少一个因子。与素因数分解相关的最基本定理是算术基本定理（又称唯一分解定理）。该定理指出：每个大于 1 的整数都可以分解为素数的乘积，并且这种分解在因子顺序之外是唯一的。例如：$120 = 2 \times 2 \times 2 \times 3 \times 5 = 2^{3} \times 3 \times 5$。\(^\text{[78][9]}\)

　　 模算术处理有限集合中的整数，并引入同余和剩余类的概念。若两个整数 $a, b$ 对模 $n$（一个正整数，称为模数）满足 $n \mid (a-b)$，则称 $a$ 与 $b$ 在模 $n$ 下同余。即在对 $a$ 与 $n$、$b$ 与 $n$ 进行欧几里得除法时得到相同的余数。这写作：$a \equiv b \pmod{n}$。类似于 12 小时制时钟，$4 + 9 = 13$，但在模 12 的意义下同余于 1。一个模 $n$ 的剩余类是包含所有与某个指定整数 $r$ 在模 $n$ 下同余的整数的集合。例如，$6\mathbb{Z} + 1$ 包含所有能表示为 $6k+1$ 的整数。

　　 模算术提供了许多公式，可以快速解决涉及大指数幂的同余问题。其中一个重要定理是费马小定理，它指出：如果素数 $p$ 与某个整数 $a$ 互素，则 $a^{p-1} \equiv 1 \pmod{p}$。欧拉定理将其推广为：对于任意整数 $n$，若 $a$ 与 $n$ 互素，则 $$ a^{\varphi(n)} \equiv 1 \pmod{n}~ $$ 其中 $\varphi(n)$ 是欧拉函数，表示小于等于 $n$ 且与 $n$ 互素的正整数的个数。模算术还提供了解决含有未知数的同余方程的公式，类似于代数方程的解法，例如中国剩余定理。\(^\text{[79]}\)

解析数论

图
图 10：复平面上的黎曼 $\zeta$ 函数 $\zeta(s)$。点 $s$ 的颜色表示 =$zeta(s)$ =的取值：深色表示值接近零，而色相表示该值的辐角。

　　 与初等数论相对，解析数论依赖于复数以及分析与微积分的技巧。解析数论可以从两个角度来定义：

　　 解析数论研究的内容包括：素数的分布、数论函数的行为以及无理数等问题。\(^\text{[81]}\)

图
图 11：模群在上半平面的作用。灰色区域是标准基本域。

　　 数论素有 “结论浅显，证明深奥” 的名声。许多数论结论可以用浅显的方式告诉普通人，但它们的证明往往并不容易理解，部分原因在于所使用的工具范围极其广泛，在数学中也算是罕见的。\(^\text{[82]}\) 解析数论中的经典问题包括：素数定理、哥德巴赫猜想、孪生素数猜想、哈代–李特伍德猜想、华林问题以及黎曼猜想。解析数论的重要工具有：圆方法，筛法，L-函数（以及对其性质的研究）。此外，模形式理论（以及更一般的自守形式理论）在解析数论工具箱中的地位也日益核心。\(^\text{[83]}\)

　　 分析学是数学的一个分支，研究极限——即当自变量（或序列的指标）趋近某个特定值时，序列或函数所趋近的数值。例如，数列 0.9, 0.99, 0.999,…的极限是 1。在函数的语境中，当 $x \to \infty$ 时，函数 $\frac{1}{x}$ 的极限是 0。[84]复数是实数的扩展，引入了虚数单位 $i$，其定义满足 $i^2 = -1$。【85】每一个复数都可以表示为 $x + i y$，其中 $x$ 称为实部 $y$ 称为虚部。

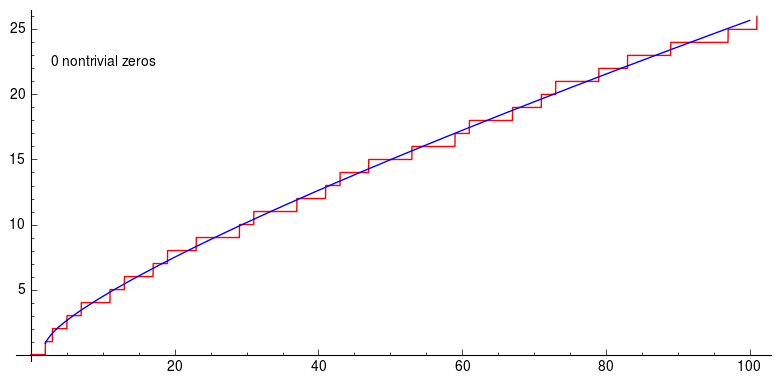
　　 素数的分布由函数 $\pi(x)$ 描述，该函数统计所有小于等于给定实数的素数个数。素数的分布是不可预测的，是数论中的主要研究对象之一。虽然已经发展出一些素数的初等公式，例如欧拉的素数多项式，能生成部分素数序列，但随着素数变大，这些公式就不再适用。解析数论中的素数定理形式化了这样一种观念：素数在数值增大的同时出现得越来越稀疏。一个经典的近似分布陈述是：$\frac{x}{ \log\left(x\right) }$ 能够很好地逼近 $\pi(x)$。另一种更精确的分布形式涉及到偏移的对数积分函数，它比 $\frac{x}{ \log\left(x\right) }$ 更快地收敛到 $\pi(x)$。\(^\text{[3]}\)

图
图 12：利用 $\zeta$ 函数的零点对素数计数函数估计的修正

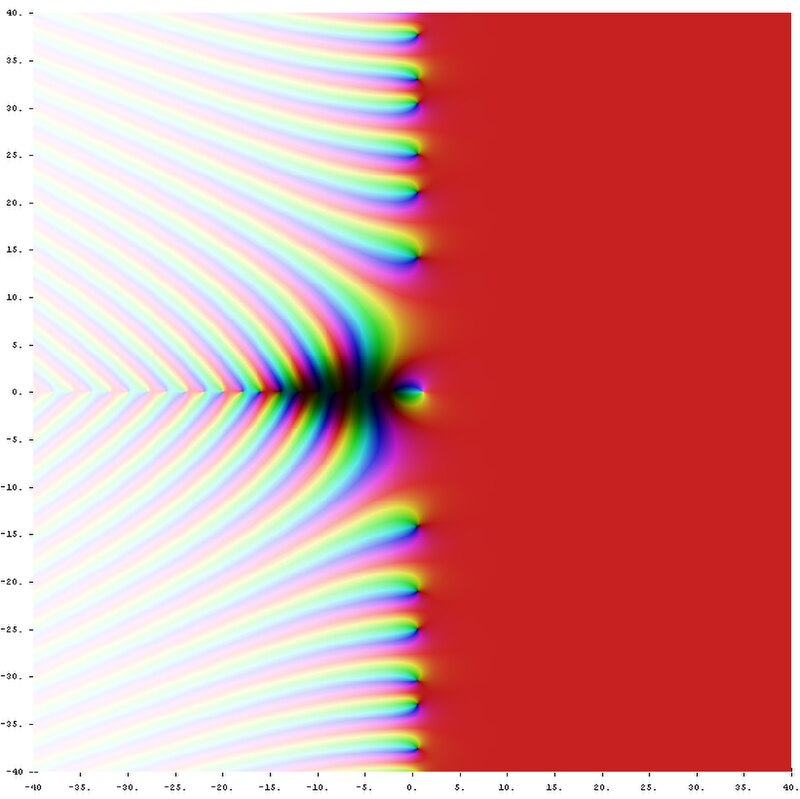
　　 $\zeta$ 函数已被证明与素数的分布密切相关。它被定义为级数： $$ \zeta(s) = \sum_{n=1}^{\infty}\frac{1}{n^s} = \frac{1}{1^s} + \frac{1}{2^s} + \frac{1}{3^s} + \cdots~ $$ 当 $s > 1$ 时，该级数收敛。欧拉证明了它与所有素数的无穷乘积之间存在联系，给出了如下恒等式： $$ \zeta(s) = \prod_{p \ \text{prime}}\left(1 - \frac{1}{p^s}\right)^{-1}.~ $$ 黎曼将 $\zeta$ 函数的定义推广到了复变量，并提出猜想：在所有非平凡零点（即 $0 < \operatorname{Re} (s) < 1$ 区间内使 $\zeta(s)=0$ 的解）中，$s$ 的实部都等于 $\frac{1}{2}$.他建立了这些非平凡零点与素数计数函数之间的联系。这就是如今著名的黎曼猜想，它仍然是数学中的悬而未决的问题。如果该猜想得到解决，将会对理解素数的分布带来直接而深远的影响。\(^\text{[86]}\) 人们可以针对代数数提出分析性的问题，并利用分析方法来解答这些问题；正是在这一点上，代数数论与解析数论相交。例如，可以定义素理想（在代数数域中对素数的推广），并询问在某个范围内共有多少个素理想。这个问题可以通过研究德德金 $\zeta$ 函数来回答，该函数是黎曼 $\zeta$ 函数的推广，而黎曼 $\zeta$ 函数则是该领域最核心的解析对象之一。\(^\text{[87]}\) 这就是解析数论中的一种普遍方法：通过研究某个适当构造的复值函数的解析性质，来推导关于某个数列（此处是素理想或素数）分布的信息。\(^\text{[88]}\)

　　 初等数论依靠的是所谓的 “初等证明”，该术语排除了复数的使用，但可能会包括一些基础分析方法。\(^\text{[72]}\) 例如，素数定理在 1896 年首先是用复分析证明的，但直到 1949 年，Erdős 和 Selberg 才找到了一个 “初等证明”。\(^\text{[89]}\) 不过，“初等” 这一术语带有一定的模糊性。例如，基于复数 Tauberian 定理（如 Wiener–Ikehara 定理）的证明，通常被认为非常有启发性，但尽管它们只使用了傅里叶分析而非复分析，却通常不被视为 “初等证明”。在这里和其他情境中，一个 “初等证明” 可能比更高深的方法对大多数读者来说更冗长、更难以理解。

　　 一些通常被视为解析数论组成部分的主题（例如筛法理论），若以 “工具” 为标准，可能更适合归入第二种定义而非第一种。\(^\text{[note 5]}\) 例如，小筛法几乎不涉及分析手段，但仍然属于解析数论的范畴。\(^\text{[note 6]}\)

代数数论

　　 代数数是指满足某个有理系数多项式方程 $f(x)=0$ 的复数。例如，方程 $x^{5}+\tfrac{11}{2}x^{3}-7x^{2}+9=0$ 的每个解 $x$ 都是代数数。由代数数组成的域称为代数数域，或简称数域。代数数论主要研究代数数域。\(^\text{[90]}\)

　　 可以认为，最简单的一类数域，即二次扩域，已经被高斯研究过了，因为他在《算术研究》中关于二次型的讨论，可以用现代语言改写为关于二次域中的理想与范数的讨论。（一个二次域由所有形如 $a+b\sqrt{d}$ 的数构成，其中 $a, b$ 是有理数，而 $d$ 是一个平方根不是有理数的有理数。）事实上，十一世纪的 chakravala 方法，用现代术语来说，本质上就是一个求解实二次数域的单位元的算法。然而，无论是 Bhāskara 还是 Gauss，在他们的时代都尚未意识到 “数域” 这一概念本身。

　　 这一学科的基础在 19 世纪晚期得以奠定，当时引入了理想数、理想理论和赋值理论，这三者是互补的方法，用于处理代数数域中唯一分解失效的问题。（例如，在由有理数与 $\sqrt{-5}$ 生成的数域中，数 $6$ 可以分解为 $6 = 2 \cdot 3$ 也可以分解为 $6 = (1+\sqrt{-5})(1-\sqrt{-5})$,其中 $2, 3, 1+\sqrt{-5}, 1-\sqrt{-5}$ 都是不可约的，因此在朴素意义上类似于整数中的素数。）理想数（由库默尔 Kummer 引入）的发展最初似乎受到高次互反律研究的推动，\(^\text{[91]}\) 即二次互反律的推广。

　　 数域通常作为较小数域的扩张来研究：如果域 $L$ 含有域 $K$，则称 $L$ 是 $K$ 的扩张。（例如，复数域 $\mathbf{C}$ 是实数域 $\mathbf{R}$ 的扩张，而实数域 $\mathbf{R}$ 又是有理数域 $\mathbf{Q}$ 的扩张。）对一个给定数域的所有可能扩张进行分类，是一个困难且部分未解决的问题。阿贝尔扩张（即 $L/K$ 的伽罗瓦群 $\mathrm{Gal}(L/K)$ 是阿贝尔群的扩张）相对比较容易理解。它们的分类是类域论的核心目标，这一研究计划由 Kronecker 和 Eisenstein 在 19 世纪晚期部分发起，并在 1900–1950 年间得到大规模发展和完成。

　　 代数数论的一个活跃研究领域是岩泽理论。而当前数学中最重要的大规模研究计划之一——朗兰兹纲领，有时被描述为一种尝试：将类域论推广到非阿贝尔数域扩张。

丢番图几何

　　 丢番图几何的核心问题是：确定一个丢番图方程在何种情况下有整数或有理数解；如果存在，那么解有多少。其研究方法是将方程的解视作一个几何对象。

　　 例如，两个变量的方程定义了平面上的一条曲线。更一般地，两个或多个变量的方程或方程组，可以定义 $n$ 维空间中的一条曲线、一个曲面或其他几何对象。在丢番图几何中，人们关心的问题是：在这些曲线或曲面上是否存在有理点（所有坐标都是有理数的点）或整点（所有坐标都是整数的点）。如果存在这样的点，下一步则是问：它们有多少个？分布情况如何？一个基本的问题是：在给定的曲线或曲面上，是否存在有限个还是无限多个有理点。

　　 例如，考虑毕达哥拉斯方程：$x^{2} + y^{2} = 1$ 我们想知道它的有理解，即满足 $x$ 和 $y$ 都是有理数的点 $(x,y)$。这与寻找所有整数解 $a^{2} + b^{2} = c^{2}$ 是等价的；任何一个整数解都会给出一个有理解：$x = a/c, \quad y = b/c$.换句话说，这就是在曲线 $x^{2} + y^{2} = 1$ 上寻找所有有理坐标点。该曲线是以原点为圆心、半径为 1 的圆。

图
图 13：两个椭圆曲线的例子，即亏格为 1 且至少有一个有理点的曲线。

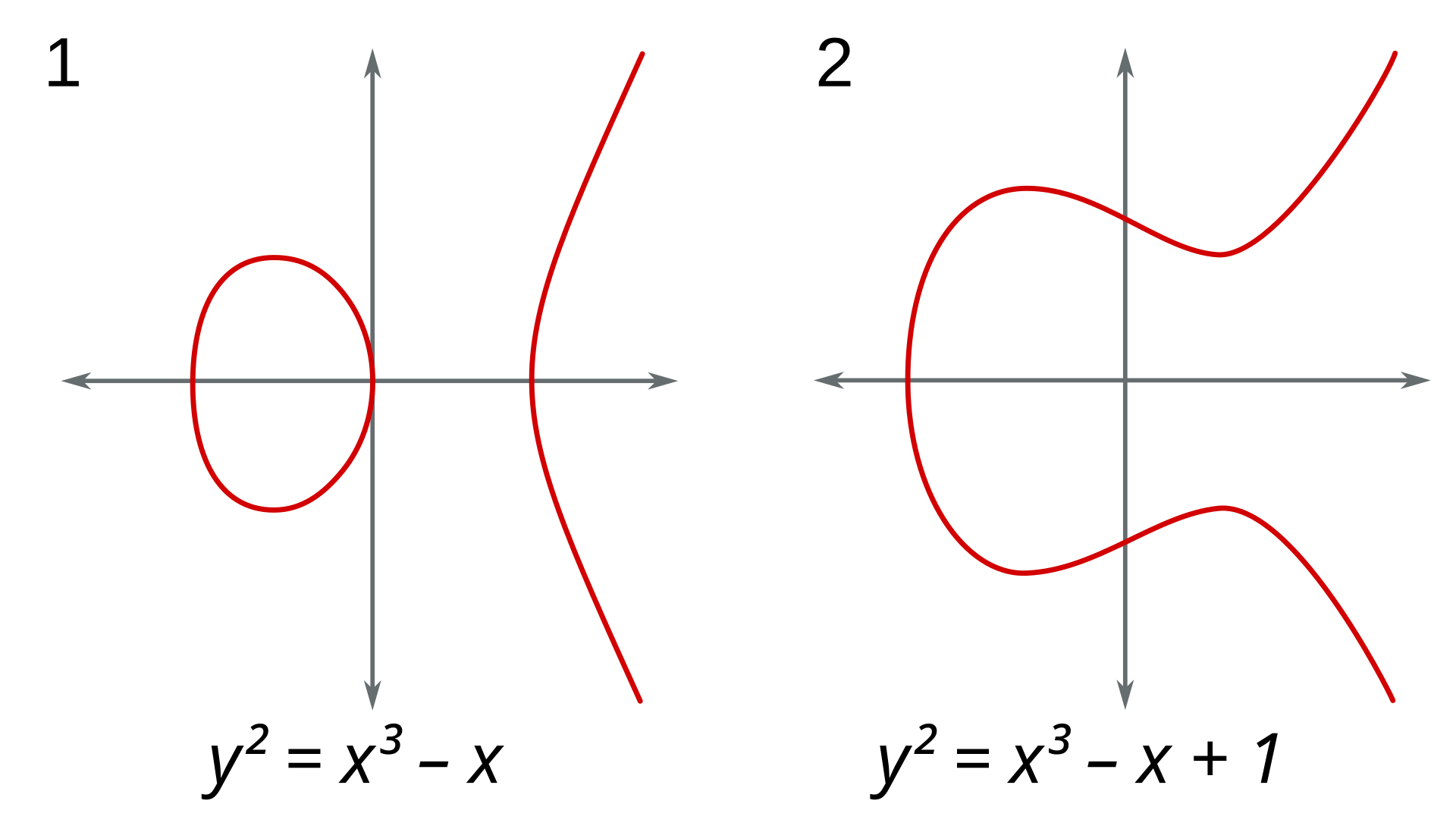
　　 将关于方程的问题重新表述为关于曲线上点的问题，是一种非常巧妙的方式。代数曲线（即两个变量的多项式方程 $f(x,y)=0$）上有理点或整点的数量是否有限，关键取决于该曲线的亏格。\(^\text{[note 8]}\) 这一研究方法的一项重大成果就是怀尔斯对费马大定理的证明，其中其他几何学概念同样发挥了至关重要的作用。

　　 另一个紧密相关的领域是丢番图逼近：给定一个数 $x$，研究它能够被有理数逼近的精确程度。人们寻找相对于分母书写复杂度而言 “良好” 的逼近。具体来说，如果 $\gcd(a,q)=1, \quad \left|x-a/q\right| < \frac{1}{q^{c}}$,其中 $c$ 较大，则称 $\tfrac{a}{q}$ 是 $x$ 的一个良好逼近。这个问题在 $x$ 为代数数时尤其重要。如果某个数不能被很好地逼近，那么某些方程就不会有整数或有理解。此外，若干概念（尤其是 “高度” height）在丢番图几何和丢番图逼近中都至关重要。这一问题在超越数论中也具有特殊意义：如果一个数能被比任何代数数更好地逼近，那么它就是一个超越数。正是通过这种论证，人们证明了 $\pi$ 和 $e$ 是超越数。

　　 需要注意的是，丢番图几何不应与数的几何混淆，后者是一种利用图解方法回答某些代数数论问题的工具集合。而算术几何则是丢番图几何的当代理论名称，尤其当人们希望强调它与现代代数几何（如法尔廷斯定理）之间的联系时，而不是仅仅强调与丢番图逼近技术的关联。

其他分支领域

　　 概率数论从这样的问题开始：随机取一个 1 到一百万之间的整数 $n$。它是质数的可能性有多大？（这其实就是在问一百万以内有多少个质数）。平均而言，$n$ 会有多少个质因子？它比平均情况多得多或少得多的因子或质因子的概率是多少？

　　 数论中的组合学从这样的问题开始：一个相当‘稠密’的无限集合 $A$ 是否包含许多处于等差数列中的元素：

　　 $a, , a+b, , a+2b, , a+3b, \ldots, a+10b$？是否有可能把大的整数写成集合 $A$ 中元素的和？”

图
图 14：莱默筛法机，一种原始的数字计算机，用于寻找质数并解简单的丢番图方程。

　　 这里有两个主要问题：‘能否计算？’以及‘能否快速计算？’任何人都可以检验一个数是否为质数，或者在它不是质数时将其分解为质因数；但要快速完成则是另一回事。如今已经有了快速的质数判定算法，但尽管在理论和实践上付出了大量努力，目前仍没有真正快速的因数分解算法。

3. 应用

　　 长期以来，数论整体，尤其是素数研究，一直被视为纯数学的典范例子，在数学之外几乎没有任何应用，除了利用素数齿轮来均匀分配磨损这一点之外。\(^\text{[92]}\) 尤其是像英国数学家 G. H. Hardy 这样的数论学家，以从事完全没有军事意义的工作为荣。\(^\text{[93]}\) 数论学家 Leonard Dickson（1874–1954）甚至说过：“感谢上帝，数论未被任何应用玷污。” 然而，这种观点如今已不再适用于数论。\(^\text{[94]}\)

　　 这种关于数论纯粹性的想法在 1970 年代被彻底打破，因为当时公开宣布素数可以用作公钥密码算法的基础。\(^\text{[95]}\) 像 RSA 这样的方案就建立在将大型合数分解为素因子的困难性之上。\(^\text{[96]}\) 这些应用促使人们对处理素数的算法进行了深入研究，尤其是素性测试方法，即判断给定数是否为素数的手段。素数还被用于计算机科学中的校验和、哈希表以及伪随机数生成器。

　　 1974 年，Donald Knuth 说过：“几乎所有初等数论中的定理，都以一种自然、合理的方式出现，并且与让计算机进行高速数值计算的问题紧密相关。”\(^\text{[97]}\) 初等数论常在计算机科学的离散数学课程中教授，它在数值分析中的连续问题上也有应用。\(^\text{[98]}\)

　　 如今，数论已经在多个现代领域中找到了应用，涉及范围广泛，例如：

4. 另见

5. 注释

  1. “Arithmetic”（算术）一词可能重新获得了一定的地位，可以说是受法国学界的影响。例如参见 Serre 1996。一九五二年，Davenport 仍需特别说明他所指的是 The Higher Arithmetic。Hardy 和 Wright 在其《An Introduction to the Theory of Numbers》（1938）的引言中写道：
    “我们曾一度打算将书名改为 An Introduction to Arithmetic，这是一个更为新颖、在某些方面也更为恰当的标题；但有人指出，这可能会导致对书的内容产生误解。”（见 Hardy & Wright 2008）
  2. Robson 2001，第 201 页。这一问题具有争议性，参见 Plimpton 322。Robson 的文章以一种带有论战性的笔法写成（Robson 2001，第 202 页），其目的在于 “也许……把 [Plimpton 322] 从神坛上拉下来”（Robson 2001，第 167 页）；但同时，他的结论是：
    “……问题‘这块泥板是如何计算出来的？’的答案，不必与‘这块泥板提出了什么问题？’的答案相同。第一个问题，最令人满意的答案是倒数对，这在半个世纪前就有人提出过；而第二个问题，则可能是某种直角三角形问题。”（Robson 2001，第 202 页）
    Robson 质疑了这样一种看法：即认为制作 Plimpton 322 的书吏（他必须 “为生计而工作”，不可能属于 “悠闲的中产阶级”）会在缺乏 “新数学市场” 的情况下，单凭自己 “无聊的好奇心” 去完成这一工作。（Robson 2001，第 199–200 页）
  3. 例如，参见《孙子算经》第三章第 36 题（引自 Lam & Ang 2004，第 223–224 页）：
    [36] 题现有一孕妇，年二十九岁。若妊娠期为九个月，求胎儿性别。答曰：男。 术：下四十九，加妊娠月数，减去其年。余数再依次减去：一为天，二为地，三为人，四为四时，五为五行，六为六律，七为七星（北斗），八为八风，九为九州。若余数为奇，则为男；若余数为偶，则为女。
    这是《孙子算经》中本来简明实用的论述中出现的最后一个问题。
  4. 直到十七世纪下半叶之前，学术职位仍然非常稀少，大多数数学家和科学家必须通过其他方式谋生（Weil 1984，第 159、161 页）。（当时已经出现了一些可辨识的职业实践特征，例如：寻找通信伙伴、拜访国外同事、建立私人图书馆（Weil 1984，第 160–161 页）。）局势在十七世纪晚期开始发生转变（Weil 1984，第 161 页）；科学学会在英格兰（皇家学会，1662 年）、法国（科学院，1666 年）和俄国（1724 年）相继成立。Euler 于 1726 年受邀前往俄国科学院，并于 1727 年抵达圣彼得堡（Weil 1984，第 163 页；Varadarajan 2006，第 7 页）。在这一背景下，“业余爱好者” 这一通常用于形容 Goldbach 的术语有其明确含义并且颇为合理：他被描述为一位靠做间谍谋生的文人（Truesdell 1984，第 xv 页；引自 Varadarajan 2006，第 9 页）。不过需要注意的是，Goldbach 也发表过一些数学著作，并且有时还曾担任过学术职位。
  5. 筛法理论在许多标准论著中被视为解析数论的主要分支之一；例如，参见 Iwaniec & Kowalski 2004 或 Montgomery & Vaughan 2007。
  6. 这一说法适用于某些组合型筛法，例如 Brun 筛，而不适用于 “大筛”。对后者的研究现已包括调和分析和泛函分析的思想。
  7. 扩域 $L/K$ 的伽罗瓦群由那些把 $L$ 中元素映射到 $L$ 中其他元素、同时保持 (K) 中所有元素不变的运算（同构）组成。比如，$\mathrm{Gal}(\mathbb{C}/\mathbb{R})$ 含有两个元素：恒等映射（把复数 $x+iy$ 映射到自身）以及复共轭（把 $x+iy$ 映射到 $x-iy$ 的映射）。扩域的伽罗瓦群能够揭示许多关于该扩域的关键性质。 对伽罗瓦群的研究始于Évariste Galois。用现代语言表述，他工作的主要成果是：一个方程 $f(x) = 0$ 可以用根式解（即可以用四则运算以及平方根、立方根等表达 $x$）当且仅当由该方程的根对有理数域所作的扩域，其伽罗瓦群在群论意义下是可解的。这里的 “可解” 是群论中的一个简单性质，对于有限群可以很容易检验。
  8. 亏格可以这样定义：允许方程 $f(x,y) = 0$ 中的变量取复数，那么该方程定义了一个嵌入在（射影的）四维空间中的二维曲面（因为两个复数变量可以分解成四个实数变量，即四个维度）。该曲面上甜甜圈状 “洞” 的数量称为曲线 $f(x,y) = 0$ 的亏格。

6. 参考文献

  1. Long 1972, 第 1 页。
  2. Karatsuba, A.A. (2020). 《数论》 Encyclopedia of Mathematics. Springer. 检索日期：2025-05-03。
  3. Moore, Patrick (2004). “Number theory”。见：Lerner, K. Lee；Lerner, Brenda Wilmoth（编）. The Gale Encyclopedia of Science. 第 4 卷（第 3 版）. Gale. ISBN 0-7876-7559-8。
  4. Tanton, James (2005). “Number theory”。Encyclopedia of Mathematics. 纽约：Facts On File. 第 359–360 页. ISBN 0-8160-5124-0。
  5. 洛萨诺-罗夫莱多 2019，第 xiii 页
  6. 纳格尔与纽曼 2008，第 4 页
    罗曼诺夫斯基 2008，第 302–303 页
    HC 编辑部 2022b
    MW 编辑部 2023
    布赫什塔布与佩查耶夫 2020
  7. 威尔逊 2020，第 1–2 页
    卡拉楚巴 2020
    坎贝尔 2012，第 33 页
    罗宾斯 2006，第 1 页
  8. 迪韦尔内 2010，第 v 页
    罗宾斯 2006，第 1 页
  9. 埃芬格，戈夫；马伦，加里·L. (2022). 《初等数论》. 博卡拉顿：CRC 出版社. ISBN 978-1-003-19311-1。
  10. 魏斯斯坦，埃里克·W. (2003). 《CRC 数学简明百科全书》（第 2 版）. Chapman & Hall/CRC. ISBN 1-58488-347-2。
  11. 魏斯斯坦，埃里克·W. (2003). “Whole Number”。《CRC 数学简明百科全书》（第 2 版）. Chapman & Hall/CRC. 第 3202 页. ISBN 1-58488-347-2。
  12. 佩奇 2003，第 18–19、34 页
    布赫什塔布与涅恰耶夫 2014
  13. 佩奇 2003，第 34 页
    卡拉楚巴 2014
  14. 佩奇 2003，第 34–35 页
    维诺格拉多夫 2019
  15. 库比柳斯 2018
  16. 波梅朗斯与萨尔柯齐 1995，第 969 页
  17. 波梅朗斯 2010
  18. 严 2002，第 12、303–305 页
    严 2013a，第 15 页
  19. 邓纳姆 2025
  20. 诺伊格鲍尔与萨克斯 1945，第 40 页。术语 *takiltum* 存在问题。罗布森更倾向于将其译为：“对角线的保持方形，其中去掉 1，使得短边上升……”。（罗布森 2001，第 192 页）
  21. 罗布森 2001，第 189 页。其他来源给出了现代公式 $(p^{2}-q^{2}, ; 2pq, ; p^{2}+q^{2})$。范德瓦尔登同时给出了现代公式以及实际上等同于罗布森所偏好的形式。（范德瓦尔登 1961，第 79 页）
  22. 诺伊格鲍尔（1969，第 36–40 页）详细讨论了该表，并顺带提及了以现代记号表示的欧几里得方法（1969，第 39 页）。
  23. 弗里贝里 1981，第 302 页。
  24. 范德瓦尔登 1961，第 63–75 页。
  25. 范德瓦尔登 1961，第 87–90 页。
  26. 扬布利库斯，《毕达哥拉斯传》（例如由古思里 1987 年译），引自范德瓦尔登 1961，第 108 页。另见波菲利，《毕达哥拉斯传》，第 6 段，见古思里 1987。
  27. 希罗多德（《历史》卷二·81）和伊索克拉底（《布西里斯》28），引自 Huffman 2011。关于泰勒斯，参见欧德穆斯引自普罗克洛斯，65.7（例如，莫罗 1992，第 52 页），引自 O'Grady 2004，第 1 页。普罗克洛斯使用的是罗得岛的欧德穆斯的一部著作（现已失传），《几何学家目录》。另见莫罗 1992 导言，第 xxx 页，关于普罗克洛斯可靠性的讨论。
  28. 博耶与梅兹巴赫 1991，第 82 页。
  29. 希思 1921，第 76 页。
  30. 科里，利奥 (2015). 《希腊数学传统中的作图问题与数值问题》. 《数字简史》. 牛津大学出版社. ISBN 978-0-19-870259-7。
  31. 《孙子算经》第三章，第 26 题。可见于林与洪 2004，第 219–220 页，其中包含《算经》的完整译文（基于钱 1963）。另见林与洪 2004，第 138–140 页的讨论。
  32. 通过内部证据（= 文中假设的税收制度），该文本的年代被缩小到公元 220–420 年（严敦杰）或公元 280–473 年（王玲）。参见林与洪 2004，第 27–28 页。
  33. 道本 2007，第 310 页。
  34. 利布雷希特 1973。
  35. 普洛夫克 2008，第 119 页。
  36. 巴比伦数学与印度数学之间的任何早期接触仍属推测。（普洛夫克 2008，第 42 页）
  37. 芒福德 2010，第 387 页。
  38. 阿耶波多，《阿耶波多历算书》第二章，第 32–33 偈，引自普洛夫克 2008，第 134–140 页。另见克拉克 1930，第 42–50 页。稍微更明确的 kuṭṭaka 描述后来见于婆罗摩笈多，《婆罗摩苏普塔悉檀多》卷十八，第 3–5 节（见 Colebrooke 1817，第 325 页，引自克拉克 1930，第 42 页）。
  39. 芒福德 2010，第 388 页。
  40. 普洛夫克 2008，第 194 页。
  41. 科尔布鲁克 1817，第 lxv 页，引自霍普金斯 1990，第 302 页。另见萨曹与比鲁尼 1888 序言，引自史密斯 1958，第 168 页。
  42. 平格里 1968，第 97–125 页，以及平格里 1970，第 103–123 页，引自普洛夫克 2008，第 256 页。
  43. 拉谢德 1980，第 305–321 页。
  44. 巴谢，1621，继齐兰德尔 1575 年的首次尝试之后。
  45. 魏伊 1984，第 45–46 页。
  46. “数论 | 定义、主题与历史 | 大英百科全书”。[www.britannica.com](http://www.britannica.com). 检索日期：2025-06-28。
  47. 福克纳，尼古拉斯；霍施，威廉·L. (2017). 《数与度量》. 《大英百科全书》. ISBN 978-1-5383-0042-8. 检索日期：2019-08-06。
  48. 魏伊 1984，第 92 页。
  49. 魏伊 1984，第 2、172 页。
  50. 瓦拉达拉扬 2006，第 9 页。
  51. 魏伊 1984，第 1–2 页。
  52. 魏伊 1984，第 2 页；以及瓦拉达拉扬 2006，第 37 页。
  53. 魏伊 1984，第 178–179 页。
  54. 瓦拉达拉扬 2006，第 39 页；以及魏伊 1984，第 176–189 页。
  55. 魏伊 1984，第 174 页。欧拉在给予他人荣誉时非常慷慨（瓦拉达拉扬 2006，第 14 页），但并非总是准确无误。
  56. 魏伊 1984，第 183 页。
  57. 瓦拉达拉扬 2006，第 45–55 页；另见第三章。
  58. 魏伊 1984，第 327–328 页。
  59. 魏伊 1984，第 337–338 页。
  60. 魏伊 1984，第 332–334 页。
  61. 戈尔茨坦与沙帕赫 2007，第 14 页。
  62. 引自《算术研究》序言；译文取自戈尔茨坦与沙帕赫 2007，第 16 页。
  63. 参见戈尔茨坦与沙帕赫 2007 第 5 节中的讨论。费马的书信中已出现了早期的自我意识迹象：例如，他关于数论是什么的评论，以及他认为 “丢番图的工作[…]并不真正属于[数论]”（引自魏伊 1984，第 25 页）。
  64. 阿波斯托尔 1976，第 7 页。
  65. 达文波特与蒙哥马利 2000，第 1 页。
  66. 参见达文波特与蒙哥马利 2000，第 1 节中的证明。
  67. 伊万涅茨与科瓦尔斯基 2004，第 1 页。
  68. 瓦拉达拉扬 2006，第 2.5、3.1 和 6.1 节。
  69. 格兰维尔 2008，第 322–348 页。
  70. 参见伊万涅茨与科瓦尔斯基 2004，第 1 页中关于模性的重大意义的评论。
  71. 纳森森，梅尔文·B. (2000). 《前言》. 《数论初等方法》. Springer. ISBN 0-387-98912-9。
  72. 布赫什塔布，A.A. (2014). 《初等数论》. 数学百科全书. Springer. 检索日期：2025-05-03。
  73. 罗曼诺夫斯基 2008，第 303 页。
  74. 穆瑟，彼得森与伯格 2013，第 101–102 页。
  75. 里士满与里士满 (2009)，第 3.4 节（整除性测试），第 102–108 页。
  76. 奥雷，奥伊斯坦 (1948). 《数论及其历史》（第 1 版）. 麦格劳-希尔出版社。
  77. 沃特金斯，约翰·J. (2014). 《整除性》. 《数论：一种历史视角》. 普林斯顿大学出版社. 第 76–80 页. ISBN 978-0-691-15940-9。
  78. 纳森森，梅尔文·B. (2000). 《整除性与素数》. 《数论初等方法》. Springer. ISBN 0-387-98912-9。
  79. 坦顿，詹姆斯 (2005). 《算术基本定理》. *数学百科全书*. 纽约：Facts On File. ISBN 0-8160-5124-0。舒普，维克托 (2005). 《数论与代数的计算导论》. 剑桥大学出版社. ISBN 978-0-511-11363-5。
  80. 格兰维尔 2008，第 1 节：“主要区别在于，在代数数论中[…]人们通常考虑的是可以用精确公式给出的答案的问题，而在解析数论中[…]人们寻找的是良好的近似。”
  81. 卡拉楚巴，A.A. (2014-10-18). 《解析数论》. *数学百科全书*。
  82. 参见例如伊万涅茨与科瓦尔斯基 2004，第 1 页的开头评论。
  83. 参见伊万涅茨与科瓦尔斯基 2004 导言中的说明，第 1 页：“然而更强的是……”。
  84. 坦顿，詹姆斯. 《极限》. *数学百科全书*。
  85. 魏斯斯坦，埃里克·W. (2002). 《复数》. *CRC 数学简明百科全书*。
  86. 坦顿，詹姆斯 (2005). 《ζ函数》. *数学百科全书*。
  87. 格兰维尔 2008，第 3 节：“[黎曼] 定义了我们现在称为黎曼ζ函数的东西 […] 黎曼的深刻工作孕育了我们的学科 […]”。
  88. 参见例如蒙哥马利与沃恩 2007，第 1 页。
  89. 戈尔德菲尔德 2003。
  90. 米尔恩 2017，第 2 页。
  91. 爱德华兹 2000，第 79 页。
  92. 布莱恩特，约翰；桑格温，克里斯托弗·J. (2008). 《你的圆有多圆？——工程与数学的交汇》. 普林斯顿大学出版社. 第 178 页. ISBN 978-0-691-13118-4。
  93. 哈代，戈德弗雷·哈罗德 (2012) [1940]. 《一个数学家的辩白》. 剑桥大学出版社. 第 140 页. ISBN 978-0-521-42706-7. OCLC 922010634。数论或相对论迄今尚未被发现具有任何战争用途，而且看来在许多年内也不太可能有人会发现。
  94. 《数论的不合理有效性》，斯特凡·安德鲁斯·伯尔，乔治·E.·安德鲁斯，美国数学学会，1992，ISBN 978-0-8218-5501-0。
  95. 克拉夫特，詹姆斯·S.；华盛顿，劳伦斯·C. (2014). 《初等数论》. *数学教材系列*. CRC 出版社. 第 7 页. ISBN 978-1-4987-0269-0。
  96. 《带密码学的数论导论》（第 2 版）. Chapman and Hall/CRC. 2018. doi:10.1201/9781351664110. ISBN 978-1-351-66411-0. 存档日期：2023-03-01. 检索日期：2023-02-22。
  97. 《计算机科学及其与数学的关系》，D.E.·克努斯 – *美国数学月刊*，1974。
  98. 《数论在数值分析中的应用》，华罗庚，王元，Springer-Verlag，1981，ISBN 978-3-540-10382-0。
  99. 克里希纳，哈里 (2017). 《数字信号处理算法》. 伦敦：Routledge 出版社. ISBN 978-1-351-45497-1。
  100. 舒迈尔，丹尼尔；哈钦森，大卫·A. W. (2011). 《黎曼猜想的物理学》. *现代物理评论* 83 (2): 307–330. arXiv:1101.3116. Bibcode:2011RvMP...83..307S. doi:10.1103/RevModPhys.83.307. S2CID 119290777。
  101. 贝利斯，约翰 (2018). 《纠错码：数学导论》. Routledge. doi:10.1201/9780203756676. ISBN 978-0-203-75667-6. 检索日期：2023-02-22。
  102. 利夫内，R. (2001)，收录于奇利贝尔托，西罗；赫尔策布鲁赫，弗里德里希；米兰达，里克；泰彻，米娜（编），《通信网络与希尔伯特模形式》，载《代数几何在编码理论、物理与计算中的应用》，多德雷赫特：Springer 出版社，第 255–270 页，doi:10.1007/978-94-010-1011-5_13, ISBN 978-1-4020-0005-8，检索日期：2023-02-22。
  103. 卡特赖特，朱利安·H. E.；冈萨雷斯，迭戈·L.；皮罗，奥雷斯特；斯坦齐亚尔，多梅尼科 (2002-03-01). 《美学、动力学与音阶：黄金的联系》. *新音乐研究杂志* 31 (1): 51–58. doi:10.1076/jnmr.31.1.51.8099. hdl:10261/18003. ISSN 0929-8215. S2CID 12232457。

来源

7. 延伸阅读

　　 该主题最受欢迎的两本入门书是：

　　 哈代与赖特的著作是一部内容全面的经典之作，但由于作者坚持使用初等方法，其清晰度有时受到影响（Apostol 1981）。维诺格拉多夫的主要吸引力在于其中的问题集，这些问题很快就引向维诺格拉多夫本人的研究兴趣；而正文本身则非常基础，接近最简。其他受欢迎的入门书包括：

　　 作为第二本教材的常见选择包括：

8. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利