群论（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　 在抽象代数中，群论研究的是称为 “群” 的代数结构。群的概念是抽象代数的核心：其他著名的代数结构，如环、域和向量空间，都可以看作是带有附加运算和公理的群。群在数学的许多领域中反复出现，而群论的方法也影响了代数的许多部分。线性代数群和李群是群论的两个分支，它们各自都有显著的发展，逐渐成为独立的研究领域。

　　 许多物理系统，例如晶体和氢原子，以及宇宙中已知四种基本相互作用力中的三种，都可以通过对称群来建模。因此，群论及其密切相关的表示论在物理学、化学和材料科学中有着重要的应用。群论在公钥密码学中同样占据核心地位。

　　 群论的早期历史可以追溯到 19 世纪。20 世纪最重要的数学成就之一，是一个合作性的巨大工程，耗费了超过一万页期刊论文，主要发表于 1960 年至 2004 年，最终完成了有限单群的完整分类。

1. 历史

　　 群论有三个主要的历史来源：数论、代数方程理论和几何学。数论的脉络由莱昂哈德·欧拉开启，后由高斯在模算术以及与二次域相关的加法群和乘法群的研究中发展。关于置换群的早期成果来自拉格朗日、鲁菲尼和阿贝尔，他们在寻找高次多项式方程的一般解时做出了贡献。埃瓦里斯特·伽罗瓦创造了 “群” 这一术语，并建立了群论与域论之间的联系，这就是如今所称的伽罗瓦理论。在几何学中，群首先在射影几何中变得重要，后来又在非欧几何中发挥作用。费利克斯·克莱因的《埃尔兰根纲领》宣称群论是几何学的组织原则。

　　 伽罗瓦在 19 世纪 30 年代率先使用群来判定多项式方程的可解性。阿瑟·凯莱和奥古斯丁·路易·柯西进一步推动了这一研究，创建了置换群理论。群的第二个历史来源源自几何情境。为了解释可能的几何体系（如欧几里得几何、双曲几何或射影几何），费利克斯·克莱因提出了 “埃尔兰根纲领”。索福斯·李在 1884 年开始将群（现称李群）引入解析问题。第三，群最初是隐含使用，后来则明确应用于代数数论中。

　　 这些早期来源的不同研究范围导致了群概念的多种表述。自约 1880 年起，群论开始趋于统一。从那时起，群论的影响不断扩大，推动了 20 世纪初抽象代数、表示论以及更多重要分支领域的诞生。有限单群的分类是 20 世纪中期的一项庞大工程，完成了对所有有限单群的分类。

2. 群的主要类别

　　 被研究的群类逐渐从有限置换群和一些特殊的矩阵群例子扩展到抽象群，这些抽象群可以通过生成元与关系的表示来定义。

置换群

　　 最早得到系统研究的群类是置换群。给定一个集合 $X$ 和一个由 $X$ 到自身的双射（称为置换）组成的集合 $G$，如果 $G$ 在复合与取逆运算下封闭，那么 $G$ 就是一个在 $X$ 上作用的群。如果 $X$ 有 $n$ 个元素而 $G$ 包含所有的置换，则 $G$ 是对称 $S_n$；一般而言，任意置换群 $G$ 都是 $X$ 的对称群的一个子群。凯莱提出的一种早期构造展示了：任何群都可以看作一个置换群，通过左正则表示作用在其自身上（即 $X = G$）。

　　 在许多情况下，可以利用置换群在相应集合上的作用性质来研究其结构。例如，通过这种方式可以证明，当 $n \geq 5$ 时，交错群 $A_n$ 是单群，即它没有任何非平凡正规子群。这个事实在说明 “对于次数 $n \geq 5$ 的一般代数方程，不能用根式求解” 时发挥了关键作用。

矩阵群

　　 下一个重要的群类是矩阵群，或称线性群。在这里，$G$ 是由某个域 $K$ 上给定阶数 $n$ 的可逆矩阵组成的集合，并且在乘法与取逆下封闭。这样的群通过线性变换作用在 $n$ 维向量空间 $K^n$ 上。这种作用使得矩阵群在概念上类似于置换群，而其作用的几何特性常常可以用来揭示群 $G$ 的性质。

变换群

　　 置换群和矩阵群是变换群的特殊情况：变换群是作用在某个空间 $X$ 上并保持其固有结构的群。对于置换群，$X$ 是一个集合；对于矩阵群，$X$ 是一个向量空间。变换群的概念与对称群的概念密切相关：变换群通常由所有保持某种结构的变换组成。

　　 变换群理论构成了群论与微分几何之间的桥梁。一系列源于李与克莱因的研究，关注群在流形上的作用，这种作用可能是同胚或微分同胚。群本身既可能是离散的，也可能是连续的。

抽象群

　　 在群论发展的初期阶段，大多数被研究的群都是 “具体的”，它们通过数、置换或矩阵来实现。直到 19 世纪晚期，“抽象群” 的概念才逐渐兴起。这里 “抽象” 意味着忽略元素的具体性质，以至于两个同构的群被认为是同一个群。指定抽象群的典型方式是通过生成元与关系的表示： $$ G = \langle S \mid R \rangle .~ $$ 抽象群的重要来源之一是商群（或因子群）的构造，即群 $G$ 对正规子群 $H$ 形成的商群 $G/H$。代数数域的类群是最早的商群例子之一，在数论中引起了极大兴趣。如果群 $G$ 是集合 $X$ 上的置换群，那么商群 $G/H$ 不再作用于 $X$；但抽象群的概念使得人们不必担心这种差异。

　　 从具体群到抽象群的视角转变，使得研究群的那些不依赖于特定实现的性质变得自然而然。换言之，就是研究在同构下保持不变的性质，以及具有这种性质的群类：有限群、周期群、单群、可解群等等。与其探索某个单独群的性质，人们更倾向于建立适用于整类群的结论。这一新范式对数学的发展具有极其重要的意义：它预示了抽象代数的诞生，这一进程体现在希尔伯特、埃米尔·阿廷、埃米·诺特及其学派的研究工作中。

具有附加结构的群

　　 当群 $G$ 被赋予附加结构时（尤其是拓扑空间、可微流形或代数簇的结构），群的概念得到了重要扩展。如果群的乘法和取逆运算与这些结构相容，即它们分别是连续的、光滑的或正规的（代数几何意义下的）映射，那么 $G$ 就是一个拓扑群、李群或代数群。

　　 附加结构的存在将这些类型的群与其他数学学科联系起来，并意味着在研究它们时可以使用更多工具。拓扑群为抽象调和分析提供了自然的领域，而李群（常常以变换群的形式出现）是微分几何与酉表示论的支柱。某些无法在一般情形下解决的分类问题，可以在群的特殊子类中得到探讨与解决。例如，紧连通李群已经得到了完整分类。无限抽象群与拓扑群之间也存在着富有成效的联系：当群 $\Gamma$ 可以作为拓扑群 $G$ 中的一个格点子群实现时，与 $G$ 相关的几何和分析结果就能为 $\Gamma$ 提供重要结论。

　　 在有限群理论中，相对较新的研究趋势是利用它们与紧拓扑群（即有限拓扑群，profinite groups）的联系。例如，一个 $p$-进解析群 $G$ 拥有一族商群，它们是各种阶数的有限 $p$-群，而 $G$ 的性质可以转化为其有限商群的性质。

3. 群论的分支

有限群论

　　 在 20 世纪，数学家们对有限群理论的一些方面进行了深入研究，尤其是有限群的局部理论，以及可解群和幂零群的理论。其结果之一是有限单群的完全分类得以实现，这意味着所有可以作为构造其他有限群基石的单群现已全部被认识。

　　 在 20 世纪下半叶，谢瓦雷、斯坦伯格等数学家也加深了我们对经典群的有限类比及其他相关群的理解。其中一个重要的群族是有限域上的一般线性群。有限群经常出现在对数学或物理对象的对称性研究中，当这些对象只允许有限个保持结构的变换时，就会涉及有限群。李群理论可以被视为研究 “连续对称性” 的理论，它与相关的魏尔群密切相关。魏尔群是由反射生成的有限群，它们作用在有限维欧几里得空间上。因此，有限群的性质在理论物理与化学等学科中也能发挥重要作用。

群的表示

　　 称群 $G$ 在集合 $X$ 上作用，意味着 $G$ 的每个元素都在集合 $X$ 上定义了一个与群结构相容的双射映射。当 $X$ 具有更多结构时，这一概念可以进一步限定：群 $G$ 在向量空间 $V$ 上的一个表示，就是一个群同态： $$ \rho : G \to \operatorname{GL}(V),~ $$ 其中 $\operatorname{GL}(V)$ 是 $V$ 上的可逆线性变换群。换句话说，每个群元素 $g$ 被对应到一个自同构 $\rho(g)$，并且满足 $\rho(g) \circ \rho(h) = \rho(gh)$ 对所有 $h \in G$ 成立。

　　 这个定义可以从两个方向理解，这两个方向各自开辟了全新的数学领域。[3] 一方面，它可能提供关于群 $G$ 的新信息：群运算通常是抽象定义的，但通过 $\rho$，它对应于矩阵的乘法，而矩阵乘法是具体且易于处理的。[4] 另一方面，当一个已充分理解的群作用在一个复杂对象上时，这会简化对该对象的研究。例如，如果 $G$ 是有限群，已知上述的 $V$ 可以分解为不可约部分（见马施克定理）。这些部分反过来比整体的 $V$ 更容易处理（通过舒尔引理）。

　　 给定一个群 $G$，表示论接着要问：$G$ 有哪些表示？根据不同背景，使用的方法和得到的结果各不相同：有限群的表示论与李群的表示论是该理论的两个主要分支。群的所有表示由其特征所支配。例如，傅里叶多项式可以理解为群 $U(1)$（即模为 1 的复数群）在周期函数的 $L^2$ 空间上作用时的特征。

李理论

　　 李群是既是群又是可微流形的数学对象，其群运算与光滑结构相容。李群以索福斯·李的名字命名，他奠定了连续变换群理论的基础。术语 groupes de Lie 首次出现于 1893 年，在李的学生阿尔图尔·特雷斯的论文第 3 页中。[5]

　　 李群体现了对数学对象与结构的连续对称性的最成熟理论，使它们成为当代数学许多领域以及现代理论物理学中不可或缺的工具。李群为分析微分方程的连续对称性（微分伽罗瓦理论）提供了自然的框架，这与伽罗瓦理论中利用置换群分析代数方程的离散对称性极为相似。将伽罗瓦理论扩展到连续对称群的情形，正是李研究工作的主要动机之一。

组合群论与几何群论

　　 群可以通过不同的方式来描述。有限群可以通过列出包含所有可能乘法 $g \cdot h$ 的群表来描述。更为紧凑的一种定义群的方式是通过生成元与关系，这也称为群的表示。给定一组生成元 $F = { g_i }_{i \in I}$，由 $F$ 生成的自由群满射到群 $G$。该映射的核称为关系子群，由某个子集 $D$ 生成。群的表示通常记作 $\langle F \mid D \rangle $.例如，表示 $\langle a, b \mid aba^{-1}b^{-1} \rangle$ 描述了一个同构于 $\mathbb{Z} \times \mathbb{Z}$ 的群。由生成元符号及其逆元组成的字符串称为 “字”。

　　 组合群论从生成元和关系的角度研究群。[6] 它在有限性假设成立时特别有用，例如有限生成群或有限表示群（即关系集也是有限的）。该领域利用了图与其基本群之间的联系。该领域的一个基本定理是：自由群的任意子群都是自由群。

　　 通过群的表示方式，会自然引出一些问题。字问题问的是两个字是否实际上表示同一个群元素。通过将该问题与图灵机联系，可以证明一般情形下不存在解决该任务的算法。另一个通常更难的、同样在算法上不可解的问题是群同构问题，即问由不同表示给出的两个群是否实际上同构。例如，表示 $\langle x, y \mid xyxyx = e \rangle$ 的群同构于整数加法群 $\mathbb{Z}$，尽管这并非一目了然。（令 $z = xy$，则有 $ G \cong \langle z, y \mid z^3 = y \rangle \cong \langle z \rangle $）

　　 几何群论从几何视角来解决这些问题，要么将群视为几何对象，要么寻找群所作用的合适几何对象。[7]第一个思想通过凯莱图得到形式化：其顶点对应于群元素，边对应于群中的右乘。给定两个元素，可以构造字度量，即它们之间最短路径的长度。米尔诺与斯瓦尔茨的一个定理表明：若一个群 $G$ 以合理的方式作用在一个度量空间 $X$ 上（例如在一个紧流形上），那么群 $G$ 与空间 $X$ 是拟等距的（即从大尺度上看二者是相似的）。

4. 群与对称性的联系

　　 给定任意一种结构化对象 (X)，一个对称性是该对象到其自身的映射，并保持该结构。在许多情况下都会出现这种情形，例如：

• 如果 $X$ 是一个没有附加结构的集合，那么一个对称性就是集合到自身的双射映射，由此产生置换群。
• 如果对象 $X$ 是平面上的点集并带有度量结构，或者是任意其他度量空间，那么一个对称性就是保持任意两点之间距离的集合自同构映射（即等距映射）。对应的群称为 $X$ 的等距群。
• 如果改为保持角度不变，则称为**保角映射**。保角映射会产生诸如 Kleinian 群的结构。

　　 对称性并不限于几何对象，也包括代数对象。例如，方程 $x^{2} - 3 = 0$ 有两个解：$\sqrt{3}$ 和 $-\sqrt{3}$。在这种情况下，交换这两个根的群就是属于该方程的伽罗瓦群。每一个单变量多项式方程都有一个伽罗瓦群，即在其根上的某个置换群。

　　 对称性构成一个群：它们是封闭的，因为如果你对一个对象施加一个对称变换，再施加另一个对称变换，结果依然是一个对称变换。保持对象不动的恒等变换总是对象的一个对称性。逆元的存在性由 “撤销” 该对称变换所保证，而结合律则源于对称性在某个空间上是函数，而函数的复合本身就是结合的。

　　 Frucht 定理指出，每一个群都是某个图的对称群。因此，每一个抽象群实际上都可以看作是某个具体对象的对称性。

　　 所谓 “保持对象的结构” 这一说法，可以通过在范畴中工作来加以严格化。保持结构的映射就是态射，而对称群就是所讨论对象的自同构群。

5. 群论的应用

　　 群论的应用极为广泛。几乎所有抽象代数中的结构都是群的特例。例如，环可以被看作是一个阿贝尔群（对应加法），再加上另一个运算（对应乘法）。因此，群论的论证构成了这些结构理论中很大一部分的基础。

伽罗瓦理论

　　 伽罗瓦理论利用群来描述多项式根的对称性（更准确地说，是由这些根生成的代数的自同构）。伽罗瓦理论的基本定理建立了代数域扩张与群论之间的联系。它给出了一个有效的判据：判断一个多项式方程是否可解，可以通过对应的伽罗瓦群是否可解来决定。

　　 例如，五阶对称群 $S_{5}$ 是不可解群，这意味着一般五次方程不能像低次数方程那样用根式来求解。作为群论的历史渊源之一，伽罗瓦理论至今仍被富有成效地应用于许多领域，例如类域论等，并不断产生新的成果。

代数拓扑

　　 代数拓扑是另一个将群与所研究对象紧密联系起来的领域。在这里，群被用来描述拓扑空间的某些不变量。之所以称为 “不变量”，是因为它们的定义方式保证了当空间发生某些形变时，这些量不会改变。例如，基本群用于 “计数” 空间中本质上不同的路径数。庞加莱猜想就是这一思想的突出应用，它在 2002/2003 年由格里戈里·佩雷尔曼证明。

　　 不过，这种影响并非单向的。例如，代数拓扑会用到 Eilenberg–MacLane 空间，即具有预设同伦群的空间。同样地，代数 $K$ 理论在某种意义上依赖于群的分类空间。最后，无限群的挠子群这一名称本身，就显示了拓扑在群论中的遗产。

代数几何

　　 代数几何同样在许多方面运用群论。前文已经介绍过阿贝尔簇。群运算的存在提供了额外的信息，使得这些簇在研究上尤其容易处理。它们也常常作为新猜想的检验对象（例如在某些情况下的 霍奇猜想）。一维情形，即椭圆曲线，得到了特别深入的研究。它们在理论上和实际应用中都极具吸引力。

　　 另一方面，环面簇是带有环面作用的代数簇。环面嵌入最近在代数几何中取得了进展，特别是在奇点解消问题上。

代数数论

　　 代数数论在一些重要应用中使用群。例如，欧拉乘积公式： $$ \sum_{n \geq 1} \frac{1}{n^{s}} ;=; \prod_{p ;\text{prime}} \frac{1}{1 - p^{-s}},~ $$ 体现了任何整数都能以唯一的方式分解为素数。该命题在更一般的环中不成立，由此引出了类群和正则素数的概念，这些内容出现在库默尔处理费马大定理的过程中。

调和分析

　　 在李群和某些其他群上的分析被称为调和分析。Haar 测度，即在李群平移下不变的积分，被用于模式识别以及其他图像处理技术。

组合数学

　　 在组合数学中，置换群和群作用的概念常用于简化对某类对象的计数；特别是参见伯恩赛德引理。

音乐

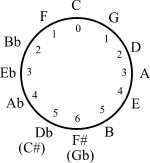
　　 在五度循环中出现的 12 周期性使得初等群论在音乐集合论中得到应用。变换理论则将音乐中的各种变换建模为数学群的元素。

物理学

　　 在物理学中，群之所以重要，是因为它们描述了物理定律所遵循的对称性。根据诺特定理，物理系统的每一个连续对称性都对应于该系统的一个守恒定律。物理学家对群的表示非常感兴趣，尤其是李群的表示，因为这些表示往往指示着 “可能的” 物理理论。群在物理中的应用例子包括：标准模型、规范理论、洛伦兹群以及庞加莱群。

　　 群论还可用于解决 Willard Gibbs 提出的力学统计解释中的不完备性问题，这涉及如何将无限多个概率求和以得到一个有意义的解。

化学与材料科学

　　 在化学与材料科学中，点群被用来对正多面体以及分子的对称性进行分类，而空间群则用于对晶体结构进行分类。确定的群随后可以用来判断物理性质（如化学极性和手性）、光谱学性质（特别是在拉曼光谱、红外光谱、圆二色光谱、磁圆二色光谱、紫外/可见光光谱以及荧光光谱中的应用），并用于构建分子轨道。

　　 分子对称性决定了许多化合物的物理和光谱性质，同时也提供了关于化学反应如何发生的重要信息。为了给定一个分子分配点群，必须找到其具有的一组对称操作。对称操作是一种作用，例如围绕某个轴的旋转或通过某个镜面的反射。换句话说，这是一种使分子在操作后与原始构型无法区分的操作。在群论中，旋转轴和镜面被称为对称元素。这些元素可以是点、直线或平面，相对于它们进行对称操作。分子的对称操作决定了该分子所属的具体点群。

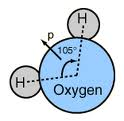
　　 在化学中，有五种重要的对称操作。它们分别是：恒等操作 $E$、旋转操作或正规旋转 $C_n$、反射操作 $\delta$、反演 $i$ 以及旋转反射操作或非正规旋转 $S_n$。恒等操作 $E$：保持分子原样不动。这相当于围绕任意轴进行任意次的整周旋转。恒等操作是所有分子的对称性，而一个手性分子的对称群只包含恒等操作。即便一个分子没有其他对称性，它也一定具有恒等操作。绕轴旋转 $C_n$：分子绕某一特定轴旋转一个特定角度。旋转角度为 $360^\circ/n$，其中 $n$ 是整数。例如，水分子绕通过氧原子且位于氢原子之间的轴旋转 $180^\circ$，会得到与起始状态完全相同的构型。在这种情况下，$n=2$，因为连续施加两次操作就等价于恒等操作。若分子具有多个旋转轴，$n$ 值最大的 $C_n$ 轴就是最高阶旋转轴或主轴。例如，在三氟化硼 $BF_3$ 中，最高阶旋转轴为 $C_3$，因此主旋转轴是 $C_3$。

　　 反射操作 $\delta$：许多分子都具有镜面，尽管不一定显而易见。反射操作交换左右，就好像每个点垂直穿过该平面，移动到与原来距离相等的另一侧位置。当该平面垂直于主旋转轴时，称为 $\delta_h$（水平镜面）；若该平面包含主旋转轴，则称为 $\delta_v$（垂直镜面）或 $\delta_d$（二面角镜面）。

　　 反演 $i$ 是一种更复杂的操作。每个点都会穿过分子的中心点，移动到与原始位置相对、且距离中心点相等的位置。许多分子乍看似乎有反演中心，但实际上没有；例如，甲烷和其他四面体分子就缺乏反演对称性。为了理解这一点，可以想象一个甲烷分子模型：两个氢原子位于右侧的竖直平面上，另两个氢原子位于左侧的水平平面上。经过反演操作后，两个氢原子会出现在右侧的水平平面上，另两个则出现在左侧的竖直平面上。因此，反演并不是甲烷的一个对称操作，因为分子在反演之后的取向与原始取向不同。最后一种操作是非正规旋转或旋转反射操作 $S_n$，它需要先进行 $360^\circ/n$ 的旋转，然后再经过垂直于旋转轴的平面进行反射。

密码学

　　 在椭圆曲线密码学中构造的大素数阶群用于公钥密码学。此类密码方法得益于几何对象及其群结构的灵活性，以及这些群复杂的结构，使得离散对数问题极难计算。最早的加密协议之一——凯撒密码，也可以解释为一种（非常简单的）群运算。大多数密码学方案在某种程度上都会使用群。尤其是，Diffie–Hellman 密钥交换使用有限循环群。因此，“基于群的密码学” 这一术语主要是指那些使用无限非阿贝尔群（如辫群）的密码协议。

6. 参见

• 群论主题列表
• 群的例子
• Bass–Serre 理论

7. 注释

1. Elwes, Richard (2006 年 12 月), “An enormous theorem: the classification of finite simple groups”, *Plus Magazine* (41)，2009-02-02 存档，2011-12-20 检索。
2. 这种施加额外结构的过程，已经通过 “适当范畴中的群对象” 这一概念形式化。因此，李群就是可微流形范畴中的群对象，而仿射代数群则是仿射代数簇范畴中的群对象。
3. 例如群上同调或等变 (K) 理论。
4. 特别是在表示是忠实表示的情况下。
5. Arthur Tresse (1893), “Sur les invariants différentiels des groupes continus de transformations”, Acta Mathematica, 18: 1–88, doi:10.1007/bf02418270。
6. Schupp & Lyndon 2001。
7. La Harpe 2000。
8. 参见千禧难题之一：Birch 与 Swinnerton-Dyer 猜想。
9. Abramovich, Dan; Karu, Kalle; Matsuki, Kenji; Wlodarczyk, Jaroslaw (2002), “Torification and factorization of birational maps”, Journal of the American Mathematical Society, 15 (3): 531–572, arXiv:math/9904135, doi:10.1090/S0894-0347-02-00396-X, MR 1896232, S2CID 18211120。
10. Lenz, Reiner (1990), Group theoretical methods in image processing, Lecture Notes in Computer Science*, vol. 413, Berlin, New York: Springer-Verlag, doi:10.1007/3-540-52290-5, ISBN 978-0-387-52290-6, S2CID 2738874。
11. Norbert Wiener, Cybernetics: Or Control and Communication in the Animal and the Machine, ISBN 978-0262730099, 第 2 章。

8. 参考文献

• Borel, Armand (1991), Linear algebraic groups, Graduate Texts in Mathematics, vol. 126 (第 2 版), 柏林, 纽约: Springer-Verlag, doi:10.1007/978-1-4612-0941-6, ISBN 978-0-387-97370-8, MR 1102012。
• Carter, Nathan C. (2009), Visual group theory, Classroom Resource Materials Series, Mathematical Association of America, ISBN 978-0-88385-757-1, MR 2504193。
• Cannon, John J. (1969), "Computers in group theory: A survey", Communications of the ACM, 12: 3–12, doi:10.1145/362835.362837, MR 0290613, S2CID 18226463。
• Frucht, R. (1939), "Herstellung von Graphen mit vorgegebener abstrakter Gruppe", Compositio Mathematica, 6: 239–50, ISSN 0010-437X, 2008-12-01 存档。
• Golubitsky, Martin; Stewart, Ian (2006), "Nonlinear dynamics of networks: the groupoid formalism", Bull. Amer. Math. Soc. (N.S.), 43 (3): 305–364, doi:10.1090/S0273-0979-06-01108-6, MR 2223010。展示了从群推广到群胚的优势。
• Judson, Thomas W. (1997), Abstract Algebra: Theory and Applications。一本面向本科生的入门教材，风格类似 Gallian 或 Herstein，涵盖群、环、整环、域及伽罗瓦理论。可免费下载 PDF，采用开源 GFDL 许可。
• Kleiner, Israel (1986), "The evolution of group theory: a brief survey", Mathematics Magazine, 59 (4): 195–215, doi:10.2307/2690312, ISSN 0025-570X, JSTOR 2690312, MR 0863090。
• La Harpe, Pierre de (2000), Topics in geometric group theory, University of Chicago Press, ISBN 978-0-226-31721-2。
• Livio, M. (2005), The Equation That Couldn't Be Solved: How Mathematical Genius Discovered the Language of Symmetry, Simon & Schuster, ISBN 0-7432-5820-7。通过解释群论如何揭示物理和其他科学中的对称性，传达群论的实际价值。
• Mumford, David (1970), Abelian varieties, Oxford University Press, ISBN 978-0-19-560528-0, OCLC 138290。
• Ronan, M. (2006), Symmetry and the Monster, Oxford University Press, ISBN 0-19-280722-6。面向普通读者，描述了寻找有限群基本构件的探索。
• Rotman, Joseph (1994), An introduction to the theory of groups, New York: Springer-Verlag, ISBN 0-387-94285-8。一部当代标准参考书。
• Schupp, Paul E.; Lyndon, Roger C. (2001), Combinatorial group theory, 柏林, 纽约: Springer-Verlag, ISBN 978-3-540-41158-1。
• Scott, W. R. (1987) [1964], Group Theory, New York: Dover, ISBN 0-486-65377-3。便宜且相当易读，但在重点、风格和符号上略显过时。
• Shatz, Stephen S. (1972), Profinite groups, arithmetic, and geometry, Princeton University Press, ISBN 978-0-691-08017-8, MR 0347778。
• Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, vol. 38, Cambridge University Press, ISBN 978-0-521-55987-4, MR 1269324, OCLC 36131259。

9. 外部链接

• 抽象群概念的历史
• Burnside, William (1911), “Groups, Theory of”, 见 Chisholm, Hugh（编）, 《大英百科全书》, 第 12 卷（第 11 版）, 剑桥大学出版社, 页 626–636。——这是该领域早期研究者对当时群论理解的详细阐述。