李群（综述）

贡献者：待更新

　　本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　在数学中，李群（Lie group，发音为 /liː/，读作 “LEE”）是既是群又是可微流形的结构，其特点是群的乘法运算和取逆运算都是可微的。

　　流形是局部上类似于欧几里得空间的空间；而群则定义了一种抽象的二元运算及其必须具备的附加性质，使其能被看作一种 “抽象变换”。例如，群可以通过乘法与逆元运算（对应于除法），或等价地，通过加法与减法来体现。将这两种概念结合，就得到了连续群，其中点的乘法和取逆运算是连续的。如果乘法和取逆进一步是光滑（可微）的，那么这样的连续群就是李群。

　　李群为连续对称性的概念提供了一种自然模型，其中著名的例子就是圆群。旋转一个圆就是连续对称性的实例。对于圆的任意一次旋转，都存在同样的对称性；而这些旋转的组合（拼接）构成了圆群，这是李群的典型例子。李群在现代数学和物理的许多领域都有广泛的应用。

　　李群最初是在研究矩阵子群 $G \subseteq \mathrm{GL}_n(\mathbb{R})$ 或 $\mathrm{GL}_n(\mathbb{C})$ 时被发现的，这里的 $\mathrm{GL}_n(\mathbb{R})$ 与 $\mathrm{GL}_n(\mathbb{C})$ 分别表示实数域 $\mathbb{R}$ 或复数域 $\mathbb{C}$ 上的 $n \times n$ 可逆矩阵群。如今，这些群被称为**经典群**，因为李群的概念已经远远超出了这些最初的范围。

　　李群的名称源自挪威数学家索弗斯·李（Sophus Lie，1842–1899），他奠定了连续变换群理论的基础。李引入李群的最初动机，是为了刻画微分方程的连续对称性，这与伽罗瓦理论中利用有限群来刻画代数方程的离散对称性有着类似的思想。

1. 历史

　　索弗斯·李认为 1873–1874 年冬天是他连续群理论的诞生时期。$^\text{[2]}$ 然而，托马斯·霍金斯则认为，应当追溯到 “李在 1869 年秋天至 1873 年秋天这四年间的惊人研究活动”，这才真正促成了该理论的建立。$^\text{[2]}$ 李的一些早期思想是在与费利克斯·克莱因的密切合作中发展起来的。从 1869 年 10 月到 1872 年，李几乎每天都与克莱因见面：从 1869 年 10 月底到 1870 年 2 月底在柏林，其后两年则在巴黎、哥廷根和埃尔兰根。$^\text{[3]}$ 李本人声称，到 1884 年时，他的主要成果都已经获得。然而，在 1870 年代，他的所有论文（除了最初的一篇简短笔记）都发表在挪威的学术期刊上，这阻碍了这些成果在欧洲其他地区的传播与认可。$^\text{[4]}$1884 年，一位年轻的德国数学家弗里德里希·恩格尔来到李身边，与他一起撰写一部系统性著作，以全面阐述连续群理论。这一合作的成果就是三卷本的《变换群论》，分别于 1888 年、1890 年和 1893 年出版。“李群” 这一术语最早于 1893 年出现，在李的学生阿图尔·特雷斯的博士论文中首次使用。$^\text{[5]}$

　　李的思想并非孤立于数学整体之外。事实上，他对微分方程几何的兴趣最初是受到卡尔·古斯塔夫·雅可比工作的启发——雅可比曾研究一阶偏微分方程理论以及经典力学中的方程。雅可比的许多成果在他去世后的 1860 年代才得以发表，这在法国和德国引起了极大的兴趣。$^\text{[6]}$ 李的执念（是建立一个微分方程对称性的理论，使其能完成与伽罗瓦在代数方程中所做的相同使命：即利用群论对它们进行分类。李和其他数学家证明，许多重要的特殊函数与正交多项式的方程，往往源于群论对称性。在李的早期工作中，他的目标是建立一个连续群的理论，以补充费利克斯·克莱因与昂利·庞加莱在模形式理论中所发展的离散群理论。李最初心中所想的应用领域，是微分方程理论。借鉴伽罗瓦理论及其在多项式方程中的作用，他的核心构想是：通过研究对称性，建立一个能够统一常微分方程整体领域的理论。然而，这一愿望并未完全实现。虽然对称性方法在常微分方程（ODE）中仍然是一个活跃的研究方向，但它并未成为该领域的主导工具。后来出现了微分伽罗瓦理论，但它是由其他数学家（如皮卡尔 Picard 和维西奥 Vessiot）发展起来的，主要提供了一种求积理论，即通过不定积分来表达解的框架。

　　进一步推动人们思考连续群的动力，来自伯恩哈德·黎曼关于几何基础的思想，以及这些思想在克莱因（Klein）手中的进一步发展。由此，李在创建他的新理论时，结合了 19 世纪数学中的三大主题：

对称性的思想 —— 伽罗瓦通过群这一代数概念所展现的典范；
几何理论与力学微分方程的显式解 —— 由泊松与雅可比所发展；
几何学的新理解 —— 在普吕克、莫比乌斯、格拉斯曼等人的研究中逐步形成，并在黎曼的革命性愿景中达到顶峰。

　　虽然今天索弗斯·李被公认为连续群理论的奠基人，但在其结构理论的发展上，一个具有决定性意义的飞跃来自威廉·基林。他在 1888 年发表了一系列题为《连续有限变换群的合成》的论文中的第一篇，这一工作对后续数学的发展产生了深远影响。$^\text{[7]}$

　　基林的成果后来被埃利·卡当加以精炼与推广，最终推动了半单李代数的分类、卡当的对称空间理论，以及赫尔曼·外尔利用最高权描述紧李群与半单李群的表示理论的建立。

　　 1900 年，大卫·希尔伯特在巴黎召开的国际数学家大会上提出了著名的希尔伯特第五星问题，向李群理论的研究者发出了挑战。

　　外尔推动了李群理论早期发展的成熟。他不仅完成了半单李群不可约表示的分类，并且将群论与量子力学建立了紧密联系；更重要的是，他通过清晰阐明李的无穷小群（即李代数）与李群本身之间的区别，使李的理论基础更加稳固，并开启了对李群拓扑结构的研究。$^\text{[8]}$ 李群理论随后在现代数学语言的框架下被系统地重新表述，这一工作体现在克洛德·谢瓦莱所撰写的专著中。

2. 概述

图 1：所有模为 1 的复数集合（对应于复平面上以原点为中心、半径为 1 的圆上的点），在复数乘法下构成一个李群，这就是圆群。

　　李群是光滑的可微流形，因此可以利用微积分进行研究，这与更一般的拓扑群情况形成对比。李群理论中的一个关键思想，是用群的局部或线性化版本来取代整体对象——李本人称之为其 “无穷小群”，后来被称为李代数。

　　李群在现代几何中具有极其重要的作用，并且体现在多个层面。费利克斯·克莱因在他的埃尔兰根纲领中指出，可以通过指定一个保持某些几何性质不变的合适变换群来考虑不同的 “几何”。因此：欧几里得几何对应于欧几里得空间 $\mathbb{R}^3$ 上保持距离不变的变换群 $E(3)$；共形几何对应于将该群扩展到共形群；射影几何则关注在射影群下保持不变的性质。这一思想后来引出了 G-结构的概念，其中 $G$ 是流形的 “局部” 对称性李群。

　　李群（及其相关的李代数）在现代物理学中发挥着重要作用，通常作为物理系统的对称性出现。在这里，李群（或其李代数）的表示具有特别重要的意义。表示论在粒子物理学中被广泛应用。其中特别重要的群包括：旋转群 $\mathrm{SO}(3)$（或其双覆盖群 $\mathrm{SU}(2)$），特殊酉群 $\mathrm{SU}(3)$，庞加莱群。

　　在 “整体” 层面上，每当一个李群作用于某个几何对象（例如黎曼流形或辛流形）时，这种作用都会带来某种刚性，并产生丰富的代数结构。通过李群在流形上的作用来表达的连续对称性的存在，会对该流形的几何结构施加强约束，并有助于在其上进行分析。李群的线性作用尤为重要，它们是表示论的核心研究对象。

　　在 1940–1950 年代，埃利斯·科尔钦、阿尔芒·博雷尔以及克洛德·谢瓦莱认识到，许多关于李群的基础性结果可以完全用代数方法来建立，从而产生了代数群理论，该理论允许在任意域上定义代数群。这一洞见为纯代数开辟了新的可能性：它不仅提供了一种对大多数有限单群的统一构造，也在代数几何中发挥了深远作用。自守形式理论作为现代数论的重要分支，与李群的类似物（定义在阿德尔环上的群）密切相关；而 p 进李群则因其与数论中伽罗瓦表示的联系，而扮演着关键角色。

3. 定义与例子

　　一个实李群是既是群又是有限维实光滑流形的对象，其中群运算（乘法与取逆）都是光滑映射。群乘法 $$ \mu : G \times G \to G, \quad \mu(x,y) = xy~ $$ 的光滑性意味着 $\mu$ 是从乘积流形 $G \times G$ 到 $G$ 的光滑映射。

　　这两个要求（乘法和取逆的光滑性）可以合并为一个条件：映射 $$ (x,y) \mapsto x^{-1}y~ $$ 是从乘积流形 $G \times G$ 到 $G$ 的光滑映射。

首批例子

所有 $2 \times 2$ 实可逆矩阵在矩阵乘法下构成一个群，称为 2 阶一般线性群，记作 $$ \operatorname{GL}(2,\mathbb{R}) \quad \text{或} \quad \operatorname{GL}_{2}(\mathbb{R}) :~ $$ $$ \operatorname{GL}(2,\mathbb{R})=\left\{A=\begin{pmatrix}a & b \\ c & d\end{pmatrix} : \det A = ad - bc \neq 0 \right\}.~ $$ 这是一个四维非紧实实李群；它是 $\mathbb{R}^4$ 的一个开子集。该群是不连通的，具有两个连通分支，分别对应于行列式取正值和负值的情况。
旋转矩阵构成 $\operatorname{GL}(2,\mathbb{R})$ 的一个子群，记 $\operatorname{SO}(2,\mathbb{R})$.它本身就是一个李群：具体来说，是一个一维紧致连通李群，并且与圆光滑同胚。若用旋转角 $\varphi$ 作为参数，则该群可参数化为： $$ \operatorname{SO}(2,\mathbb{R})=\left\{\begin{pmatrix}\cos \varphi & -\sin \varphi \\ \sin \varphi & \cos \varphi \end{pmatrix} : \varphi \in \mathbb{R} / 2\pi\mathbb{Z}\right\}.~ $$ 角度的加法对应于 $\operatorname{SO}(2,\mathbb{R})$ 中元素的乘法，而取相反角度对应于取逆运算。因此，群的乘法与取逆运算都是可微映射。
一维仿射群是一个二维矩阵李群，由所有满足对角元分别为正数和 1 的 $2 \times 2$ 实上三角矩阵组成： $$ A=\begin{pmatrix} a & b \\ 0 & 1 \end{pmatrix}, \quad a > 0, \, b \in \mathbb{R}.~ $$

非例子

　　下面给出一个具有不可数多个元素但在某种拓扑下并非李群的例子。考虑如下的群： $$ H = \left\{\begin{pmatrix} e^{2\pi i \theta} & 0 \\ 0 & e^{2\pi i a \theta} \end{pmatrix} : \theta \in \mathbb{R} \right\} \subset \mathbb{T}^2 = \left\{\begin{pmatrix} e^{2\pi i \theta} & 0 \\ 0 & e^{2\pi i \phi} \end{pmatrix} : \theta, \phi \in \mathbb{R} \right\},~ $$ 其中 $a \in \mathbb{R} \setminus \mathbb{Q}$ 是一个固定的无理数。该群 $H$ 是环面 $\mathbb{T}^2$ 的一个子群，但在子空间拓扑下，它并不是一个李群。$^\text{[9]}$ 原因是：如果我们取 $H$ 中某一点 $h$ 的任意一个小邻域 $U$，那么 $U$ 内的 $H$ 的部分是不连通的。事实上，群 $H$ 在环面上不断缠绕，但永远不会回到螺旋上的先前一点，从而在 $\mathbb{T}^2$ 中形成一个稠密子群。

　　然而，可以给群 $H$ 赋予一种不同的拓扑：在这种拓扑下，两个点 $h_{1}, h_{2} \in H$ 之间的距离定义为它们在群 $H$ 中连接 $h_{1}$ 与 $h_{2}$ 的最短路径长度。在此拓扑下，通过将每个元素与定义 $H$ 时的参数 $\theta$ 对应，$H$ 可以与实数直线建立同胚对应。由此可见，在这种拓扑下，$H$ 就是实数加法群，因此它是一个李群。

　　群 $H$ 是一个例子：它是某个李群的 “李子群”，但却不是闭子群。关于李子群的进一步讨论，见下文的基本概念部分。

图 2：群 $H$ 在环面 $\mathbb{T}^2$ 内的一部分示意图。在子空间拓扑下，元素 $h \in H$ 的小邻域在 $H$ 中是不连通的。

矩阵李群

　　记 $\operatorname{GL}(n,\mathbb{C})$ 为所有 $n \times n$ 复可逆矩阵构成的群。任何 $\operatorname{GL}(n,\mathbb{C})$ 的闭子群都是一个李群；$^\text{[10]}$ 这种类型的李群称为矩阵李群。由于大多数有趣的李群实例都可以实现为矩阵李群，一些教材（如 Hall$^\text{[11]}$、Rossmann$^\text{[12]}$ 和 Stillwell$^\text{[13]}$ 的著作）将研究范围限制在这一类上。专注于矩阵李群使得李代数与指数映射的定义更加简化。以下是一些标准的矩阵李群例子：

特殊线性群：$\operatorname{SL}(n,\mathbb{R})$ 与 $\operatorname{SL}(n,\mathbb{C})$，由所有行列式为 1 的 $n \times n$ 实矩阵或复矩阵构成。
酉群与特殊酉群：$\operatorname{U}(n,\mathbb{C})$ 与 $\operatorname{SU}(n,\mathbb{C})$，由所有满足 $ U^{*} = U^{-1}$ 的 $n \times n$ 复矩阵构成；其中在 $\operatorname{SU}(n)$ 的情形下，还要求 $\det(U) = 1$。
正交群与特殊正交群：$\operatorname{O}(n,\mathbb{R})$ 与 $\operatorname{SO}(n,\mathbb{R})$，由所有满足 $R^{\mathrm{T}} = R^{-1}$ 的 $n \times n$ 实矩阵构成；其中在 $\operatorname{SO}(n,\mathbb{R})$ 的情形下，还要求 $\det(R) = 1$。

　　上述所有例子都属于经典群的范畴。

拓扑定义

　　李群也可以定义为一个拓扑群，它在单位元附近看起来像一个变换群，而无需明确提及可微流形。$^\text{[14]}$ 首先，我们定义浸入线性的李群为一般线性群 $\operatorname{GL}(n,\mathbb{C})$ 的一个子群 $G$，并满足以下条件：

对于 $G$ 中单位元 $e$ 的某个邻域 $V$，$V$ 上的拓扑是 $\operatorname{GL}(n,\mathbb{C})$ 的子空间拓扑，并且 $V$ 在 $\operatorname{GL}(n,\mathbb{C})$ 中是闭的；$G$ 至多有可数个连通分支。

　　（例如，$\operatorname{GL}(n,\mathbb{C})$ 的任意闭子群，即矩阵李群，就满足上述条件。）

　　于是，李群可以定义为这样一种拓扑群：在单位元附近局部同构于某个浸入线性李群；至多具有可数个连通分支。证明该拓扑定义与通常的定义等价是一个技术性问题（初学者可以略过），其大致思路如下：

若以通常的流形意义给定一个李群 $G$，则通过李群–李代数对应（或李第三定理的某种形式），可以构造一个浸入的李子群 $G' \subset \operatorname{GL}(n,\mathbb{C})$ 使得 $G$ 与 $G'$ 具有相同的李代数，因此它们在局部上是同构的。由此可见，$G$ 满足上述拓扑定义。
反过来，设 $G$ 是一个满足上述拓扑定义的拓扑群，并选择一个在局部上与 $G$ 同构的浸入线性李群 $G'$。根据闭子群定理的一种形式，$G'$ 是一个实解析流形；然后通过这种局部同构，$G$ 在单位元附近获得了流形结构。进一步可以证明，$G$ 的群运算可以通过形式幂级数来描述；$^\text{[a]}$ 因此群运算是实解析的，从而 $G$ 本身就是一个实解析流形。

　　由此，拓扑定义蕴含以下结论：如果两个李群作为拓扑群同构，那么它们作为李群也同构。事实上，这表明了一个更普遍的原理：在很大程度上，李群的拓扑结构与群运算共同决定了该群的几何结构。

4. 更多李群的例子

　　李群在数学和物理中极为常见。矩阵群或代数群大体上就是矩阵的群（例如正交群和辛群），它们提供了大多数常见的李群实例。

一维与二维

　　唯一的一维连通李群是：实数直线 $\mathbb{R}$（群运算为加法）；圆群 $S^{1}$，即模为 1 的复数集合（群运算为乘法）。群 $S^{1}$ 通常记作 $\operatorname{U}(1)$，它是所有 $1 \times 1$ 酉矩阵构成的群。

　　在二维情形下，如果我们将注意力限制在单连通群，它们可以通过其李代数分类。二维的李代数（同构意义下）只有两种。相应的单连通李群是：$\mathbb{R}^{2}$（群运算为向量加法）；一维仿射群（其描述见前文 “首批例子” 部分）。

构造方法

　　有几种标准方式可以由已有的李群构造新的李群：

直积：两个李群的直积仍然是一个李群。
闭子群：李群的任意拓扑闭子群本身也是一个李群。这被称为闭子群定理或卡当定理。
商群：李群对其闭正规子群的商群也是一个李群。
普遍覆盖：连通李群的普遍覆盖仍然是一个李群。例如，实数群 $\mathbb{R}$ 是圆群 $S^{1}$ 的普遍覆盖。事实上，任意可微流形的覆盖空间本身仍是可微流形；但指定普遍覆盖可以确保存在一个与其其他结构相容的群结构。

5. 基本概念

与李群相关的李代数

　　对于每一个李群，都可以关联一个李代数。其底层向量空间是李群在单位元处的切空间，而它完全刻画了李群的局部结构。非正式地，可以将李代数的元素看作是 “无限接近” 单位元的群元素，而李代数的括号运算则与两个这样的无穷小元素的换位子相关。

　　在给出抽象定义之前，先看一些例子：

向量空间 $\mathbf{R}^n$ 的李代数就是 $\mathbf{R}^n$ 本身，其李括号为 $$ [A, B] = 0.~ $$ （一般来说，连通李群的李括号恒为 0，当且仅当该李群是阿贝尔群。）
一般线性群 $\operatorname{GL}(n,\mathbf{C})$（可逆矩阵群）的李代数是方阵空间 $M(n,\mathbf{C})$，其李括号为 $$ [A, B] = AB - BA.~ $$
若 $G$ 是 $\operatorname{GL}(n,\mathbf{C})$ 的闭子群，则其李代数可以非正式地理解为所有矩阵 $m \in M(n,\mathbf{C})$，使得 $1 + \varepsilon m \in G$，其中 $\varepsilon$ 是满足 $\varepsilon^2 = 0$ 的无穷小正数（当然，实际并不存在这样的实数 $\varepsilon$）。例如，正交群 $\operatorname{O}(n,\mathbf{R})$ 由所有满足 $AA^{T} = 1$ 的矩阵 $A$ 构成；其李代数由所有满足 $(1 + \varepsilon m)(1 + \varepsilon m)^{T} = 1$ 的矩阵 $m$ 构成，这等价于 $m + m^{T} = 0$，因为 $\varepsilon^{2} = 0$。
上述描述可以更严格地表述为：若 $G$ 是 $\operatorname{GL}(n,\mathbb{C})$ 的闭子群，则其李代数可计算为 $$ \operatorname{Lie}(G) = \{ X \in M(n,\mathbf{C}) \mid \exp\left(tX\right) \in G \ \text{for all } t \in \mathbf{R} \},~ $$ 其中 $ \exp\left(tX\right) $ 通过矩阵指数定义。[16][11]可以证明，$G$ 的李代数是一个实向量空间，并且在括号运算 $[X, Y] = XY - YX$ 下封闭。$^\text{[17]}$

　　上述针对矩阵群给出的具体定义易于操作，但存在一些小问题：使用该定义前，我们需要先把李群表示为矩阵群，但并非所有李群都能这样表示，甚至李代数是否独立于所用表示也并非显然。$^\text{[18]}$ 为了解决这些问题，我们给出李群的李代数的一般定义（分四步）：

在任意光滑流形 $M$ 上的向量场可以看作是流形上光滑函数环的导子 $X$，因此在李括号 $[X, Y] = XY - YX$ 下构成一个李代数，因为两个导子的李括号仍然是导子。
如果 $G$ 是一个在流形 $M$ 上光滑作用的群，那么它也作用于向量场空间。被群固定的不变向量场构成的向量空间在李括号下封闭，因此也构成一个李代数。
将这一构造应用到李群自身：设流形 $M$ 就是李群 $G$ 的底层空间，并且令 $G$ 通过左平移 $L_{g}(h) = gh$ 作用在自身上。由此可知，李群上所有左不变向量场（即满足 $(L_{g})_{*}X_{h} = X_{gh}, \quad \forall h \in G$ 的向量场，其中 $(L_{g})_{*}$ 表示 $L_{g}$ 的微分）在向量场的李括号下构成一个李代数。
李群在单位元处的任意切向量都可以通过左平移延拓为整个流形上的左不变向量场。具体来说，若 $v$ 是单位元处切空间中的一个元素，则它的左不变延拓向量场定义为 $v^{g} = (L_{g})_{*}v$.这样，李群在单位元处的切空间 $T_{e}G$ 就与左不变向量场空间对应，从而使得单位元处的切空间本身成为一个李代数，称为 $G$ 的李代数，通常记作 $\mathfrak{g}$。因此，$\mathfrak{g}$ 上的李括号可以明确表示为 $[v, w] = [\hat{v}, \hat{w}]_{e}$,其中 $\hat{v}, \hat{w}$ 分别是 $v, w$ 的左不变延拓。

　　这个李代数 $\mathfrak{g}$ 是有限维的，其维数与流形 $G$ 的维数相同。李群 $G$ 的李代数能决定 $G$ 的 “局部同构类”，即两个李群若在单位元附近看起来相同，就称为局部同构。许多关于李群的问题，往往先转化为对应的李代数问题来解决，然后群的结果通常就能顺理成章地得到。例如，单李群的分类通常是先对相应的李代数进行分类。

　　我们同样可以用右不变向量场而不是左不变向量场来定义单位元处的李代数结构。两者得到的是相同的李代数，因为群上的取逆映射可以把左不变向量场与右不变向量场对应起来，并且它在切空间 $T_{e}G$ 上起到 $-1$ 的作用。

　　此外，单位元处切空间上的李代数结构还可以这样描述：考虑换位子运算 $$ (x, y) \mapsto xyx^{-1}y^{-1}~ $$ 它把 $G \times G$ 中的 $(e, e)$ 送到 $e$。因此，其导数在 $T_{e}G$ 上诱导出一个双线性运算。这个双线性运算实际上是零映射，但其二阶导数在恰当的切空间同一化之下，给出了一个满足李括号公理的运算，并且它等于通过左不变向量场定义的李括号的两倍。

同态与同构

　　若 $G$ 与 $H$ 是李群，则一个李群同态 $f : G \to H$ 是一个光滑的群同态。对于复李群，这样的同态要求是全纯映射。不过，这些要求略显严格：事实上，任意实李群之间的连续同态必然是（实）解析的。$^\text{[19][b]}$

　　两个李群同态的复合仍然是一个同态，因此所有李群及其同态构成一个范畴。此外，每一个李群同态都会诱导一个对应的李代数同态。设 $\phi : G \to H$ 是一个李群同态，$\phi_{*}$ 是其在单位元处的导数。若我们将 $G$ 与 $H$ 的李代数分别与它们在单位元处的切空间对应，则 $$ \phi_{*} : \mathfrak{g} \to \mathfrak{h}~ $$ 是一个李代数同态（即它是保持李括号的线性映射）。用范畴论的语言来说，我们因此得到一个从李群范畴到李代数范畴的协变函子：它把一个李群送到其李代数，把一个李群同态送到其在单位元处的导数。

　　若存在一个双射同态，其逆映射也是李群同态，则称两个李群同构。换句话说，同构就是一个既是微分同胚又是群同态的映射。需要注意的是，根据上述结论，如果一个从李群 $G$ 到李群 $H$ 的连续同态是双射，那么它就是李群同构。

李群与李代数的同构

　　同构的李群必然具有同构的李代数；因此，自然会问：李群的同构类与李代数的同构类之间有怎样的关系？

　　第一个相关结果是李的第三定理：每一个有限维实李代数都是某个（线性）李群的李代数。证明李的第三定理的一种方法是借助阿多定理，它表明每一个有限维实李代数都同构于某个矩阵李代数。而对于任意有限维矩阵李代数，都存在一个线性群（矩阵李群），其李代数正是该矩阵李代数。$^\text{[20]}$

　　另一方面，具有同构李代数的李群不一定同构。即使假设这些群是连通的，这个结论依然成立。换句话说，李群的整体结构并不能由其李代数决定。例如，若 $Z$ 是 $G$ 的中心的某个离散子群，则 $G$ 与 $G/Z$ 具有相同的李代数（参见李群表中的例子）。在物理学中，一个重要的例子是 $\mathrm{SU}(2)$ 与 $\mathrm{SO}(3)$。这两个群的李代数是同构的，$^\text{[21]}$ 但它们自身并不同构，因为 $\mathrm{SU}(2)$ 是单连通的，而 $\mathrm{SO}(3)$ 不是。$^\text{[22]}$

　　另一方面，如果我们要求李群是单连通的，那么整体结构就由其李代数唯一决定：两个具有同构李代数的单连通李群必然同构。$^\text{[23]}$（关于单连通李群的更多信息，见下一小节。）由李的第三定理可知，有限维实李代数的同构类与单连通李群的同构类之间存在一一对应关系。

单连通李群

　　若李群 $G$ 中的任意闭合回路都能在 $G$ 内连续收缩到一点，则称 $G$ 是单连通的。这个概念之所以重要，是因为有以下定理以单连通性作为假设：

　　 定理：$^\text{[24]}$设 $G$ 与 $H$ 是李群，它们的李代数分别为 $\mathfrak{g}$ 与 $\mathfrak{h}$，并且 $f : \mathfrak{g} \to \mathfrak{h}$ 是一个李代数同态。若 $G$ 是单连通的，则存在唯一的李群同态 $\phi : G \to H$ 使得 $\phi_{*} = f$ 其中 $\phi_{*}$ 是 $\phi$ 在单位元处的微分。

　　李的第三定理表明，每一个有限维实李代数都是某个李群的李代数。结合前述结果可以推知：每一个有限维实李代数都是唯一一个单连通李群的李代数。

　　一个单连通李群的例子是特殊酉群 $\mathrm{SU}(2)$，它作为流形与三维球面 $S^{3}$ 同胚。而旋转群 $\mathrm{SO}(3)$ 则不是单连通的（参见 $\mathrm{SO}(3)$ 的拓扑）。$\mathrm{SO}(3)$ 不是单连通的事实，与量子力学中整数自旋与半整数自旋的区别有着密切关系。

　　其他单连通李群的例子包括：特殊酉群 $\mathrm{SU}(n)$，自旋群 $\mathrm{Spin}(n)$（旋转群的双覆盖，适用于 $n \geq 3$），紧辛群 $\mathrm{Sp}(n)$。$^\text{[25]}$

　　关于如何判定一个李群是否单连通的问题，可参见李群的基本群相关条目。

指数映射

　　一般线性群 $\mathrm{GL}(n;\mathbb{C})$ 的李代数 $\mathrm{M}(n;\mathbb{C})$ 到 $\mathrm{GL}(n;\mathbb{C})$ 的指数映射由矩阵指数定义，其形式是常见的幂级数： $$ \exp\left(X\right) = 1 + X + \frac{X^2}{2!} + \frac{X^3}{3!} + \cdots~ $$ 其中 $X$ 为矩阵。若 $G$ 是 $\mathrm{GL}(n;\mathbb{C})$ 的闭子群，则指数映射会将 $G$ 的李代数送入 $G$。因此，所有矩阵群都有指数映射。并且，$G$ 中每一个足够接近单位元的元素都可以表示为李代数中某个矩阵的指数。$^\text{[26]}$

　　上述定义简便易用，但它只适用于矩阵群；对于不是矩阵群的李群，该定义无法直接使用。而且，也并不显然李群的指数映射与其矩阵群表示无关。要解决这两个问题，可以采用一种更抽象的定义，它对所有李群都成立，具体如下。

　　对于李群 $G$ 的李代数 $\mathfrak{g}$（即 $G$ 在单位元处的切空间）中的每一个向量 $X$，可以证明存在唯一的一参数子群 $c : \mathbb{R} \to G$ 使得 $c'(0) = X$.

　　所谓一参数子群，意味着 $c$ 是一个到 $G$ 的光滑映射，并且满足 $$ c(s+t) = c(s)c(t), \quad \forall s,t \in \mathbb{R}~ $$ 其中右边的运算是 $G$ 中的群乘法。这个公式与实数指数函数的公式形式上极为相似，因此我们定义 $$ \exp\left(X\right) = c(1)~ $$ 这就是指数映射，它把李代数 $\mathfrak{g}$ 映射到李群 $G$。指数映射在 $\mathfrak{g}$ 中的 0 邻域与 $G$ 中的单位元 $e$ 邻域之间给出了一个微分同胚。这个指数映射是实数指数函数的推广：$\mathbb{R}$ 是正实数乘法群的李代数；$\mathbb{C}$ 是非零复数乘法群的李代数；$M(n,\mathbb{R})$（带有通常的换位子运算）是可逆矩阵群 $\mathrm{GL}(n,\mathbb{R})$ 的李代数。

　　由于指数映射在单位元邻域 $N$ 上是满射的，人们通常称李代数的元素为群 $G$ 的无穷小生成元。由该邻域 $N$ 生成的 $G$ 的子群就是 $G$ 的单位分支。

　　指数映射与李代数决定了每一个连通李群的局部群结构，这依赖 Baker–Campbell–Hausdorff 公式：存在李代数 $\mathfrak{g}$ 中零元的一个邻域 $U$，使得对所有 $X, Y \in U$,成立 $$ \exp\left(X\right) \, \exp\left(Y\right) = \exp\!\Big( X + Y + \tfrac{1}{2}[X,Y] + \tfrac{1}{12}[[X,Y],Y] - \tfrac{1}{12}[[X,Y],X] - \cdots \Big),~ $$ 其中省略的项是已知的，并涉及四个或更多元素的李括号。若 $X$ 与 $Y$ 可交换，则该公式化简为熟悉的指数律：$ \exp\left(X\right) \exp\left(Y\right) = \exp\left(X+Y\right) $.

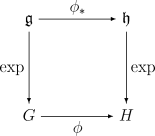
　　指数映射还联系着李群同态。也就是说，若 $\phi : G \to H$ 是一个李群同态，而 $\phi_{*} : \mathfrak{g} \to \mathfrak{h}$ 是其在对应李代数上的诱导映射，则对所有 $x \in \mathfrak{g}$，都有 $$ \phi( \exp\left(x\right) ) = \exp\left(\phi_{*}(x)\right) .~ $$ 换句话说，下图是交换的：$^\text{[27]}$

图 3

　　（简而言之，$\exp$ 是从函子 Lie 到李群范畴上的恒等函子的一个自然变换。）

　　从李代数到李群的指数映射并不总是满射，即便李群是连通的也是如此（不过，对于连通的紧李群或幂零李群，它确实是满射的）。例如，$\mathrm{SL}(2,\mathbb{R})$ 的指数映射就不是满射。此外，对于以 $C^{\infty}$ Fréchet 空间为模型的无限维李群（见下文），指数映射既不是满射，也不是单射；即便是在 0 的任意小邻域到 1 的相应邻域之间，情况仍然如此。

李子群

　　李群 $G$ 的一个李子群 $H$，是指 $H \subseteq G$，并且从 $H$ 到 $G$ 的包含映射既是单射浸入又是群同态。根据卡当定理，李群 $G$ 的任意闭子群都承认唯一的光滑结构，使其成为 $G$ 的一个嵌入李子群——即包含映射是一个光滑嵌入。

　　非闭子群的例子很多。例如，取 $G$ 为二维或更高维的环面，设 $H$ 是一个斜率为无理数的一参数子群，也就是说，它会在 $G$ 中不断缠绕。此时存在一个李群同态 $\varphi : \mathbb{R} \to G$ 使得 $\mathrm{im}(\varphi) = H$.$H$ 的闭包将是 $G$ 的一个子环面。

　　指数映射在连通李群 $G$ 的连通李子群与其李代数的子代数之间建立了一一对应关系。$^\text{[28]}$ 通常情况下，对应于某个子代数的子群并不是闭子群。仅凭 $G$ 的结构，并不存在判定哪些子代数对应于闭子群的标准。

6. 表示

　　研究李群的一个重要方面是它们的表示，即它们如何（线性地）作用在向量空间上。在物理学中，李群往往刻画物理系统的对称性。利用这些对称性来帮助分析系统的方法通常就是表示论。

　　例如，考虑量子力学中的定态薛定谔方程：$\hat{H}\psi = E\psi$.假设系统具有旋转群 $\mathrm{SO}(3)$ 的对称性，即哈密顿算符 $\hat{H}$ 与 $\mathrm{SO}(3)$ 在波函数 $\psi$ 上的作用对易。（一个典型的例子是氢原子，其势函数具有球对称性。）这个假设并不意味着解 $\psi$ 本身是旋转不变的，而是意味着对于每个固定的能量 $E$，方程 $\hat{H}\psi = E\psi$ 的解空间在旋转作用下保持不变。因而这个解空间构成了 $\mathrm{SO}(3)$ 的一个表示。这些表示已经被分类过，而分类结果大大简化了问题，本质上把一个三维偏微分方程转化为了一维常微分方程。

　　连通紧李群 $K$ 的情形（包括刚提到的 $\mathrm{SO}(3)$）尤其容易处理。$^\text{[29]}$ 在这种情况下，$K$ 的任意有限维表示都可以分解为不可约表示的直和。不可约表示的分类是由赫尔曼·外尔完成的，其依据是表示的 “最高权”。这一分类与半单李代数表示的分类密切相关。

　　此外，还可以研究任意李群（不必是紧的）的酉表示（通常是无限维的）。例如，$\mathrm{SL}(2,\mathbb{R})$ 的表示以及庞加莱群的表示，都可以得到相对明确且较为简单的描述。

7. 分类

　　李群可以被看作是平滑变化的对称族。对称性的例子包括绕某一轴的旋转。关键要理解的是那些 “微小变换” 的本质，例如微小角度的旋转，它们把相邻的变换联系起来。刻画这种结构的数学对象就是李代数（李本人称之为 “无穷小群”）。李代数之所以能被定义，是因为李群是光滑流形，因此在每一点上都有切空间。

　　任何紧李群（大致上指其对称性集合是有界的）的李代数都可以分解为一个阿贝尔李代数与若干个单李代数的直和。阿贝尔李代数的结构在数学上并无太大趣味（因为李括号恒为零）；研究的重点在于那些单李代数。由此引出了一个问题：紧群的单李代数有哪些？事实证明，它们大多数属于四个无限族，即所谓经典李代数：$A_n$、$B_n$、$C_n$、$D_n$，这些都可以用欧几里得空间的对称性来简单描述。但除此之外，还有五个不属于任何族的 “例外李代数”，其中最大的一个是 $E_8$。

　　因此，李群的分类标准包括：代数性质（单、半单、可解、幂零、阿贝尔）；连通性（是否连通或单连通）；紧性（是否紧）。

　　一个首要的关键结果是：李维分解，它表明每一个单连通李群都可以分解为一个可解正规子群与一个半单子群的半直积。

连通紧李群已经完全分类：它们是圆群 $S^1$ 的若干份直积与若干个紧单李群（对应于连通的 Dynkin 图）的直积的有限中心商。
任意单连通可解李群同构于某个秩下可逆上三角矩阵群的一个闭子群，并且此类群的任意有限维不可约表示都是一维的。可解群结构过于复杂，除了极少数低维情形外，无法进行完整分类。
任意单连通幂零李群同构于某个秩下对角线上为 1 的可逆上三角矩阵群的一个闭子群，并且此类群的任意有限维不可约表示同样是一维的。和可解群一样，幂零群也过于复杂，除了在少数低维情形下，难以进行完整分类。
单李群有时被定义为抽象群意义下的单群，有时被定义为李代数单的连通李群。例如，$\mathrm{SL}(2,\mathbb{R})$ 按后一种定义是单的，但按前一种定义则不是。无论采用哪种定义，单李群都已经被分类完毕。
半单李群是其李代数为单李代数直积的李群。$^\text{[30]}$ 它们是单李群直积的中心扩张。

　　任意李群的单位分支是一个开正规子群，而其商群是一个离散群。任意连通李群的普遍覆盖是一个单连通李群；反过来，任意连通李群都可以表示为某个单连通李群对其中心的一个离散正规子群的商。任何李群 $G$ 都可以以一种典范方式分解为离散群、单群与阿贝尔群，具体如下：
$G_{\mathrm{con}}$：单位元所在的连通分支；
$G_{\mathrm{sol}}$：最大的连通正规可解子群；
$G_{\mathrm{nil}}$：最大的连通正规幂零子群。

　　于是我们得到一列正规子群： $$ 1 \;\subseteq\; G_{\mathrm{nil}} \;\subseteq\; G_{\mathrm{sol}} \;\subseteq\; G_{\mathrm{con}} \;\subseteq\; G.~ $$ 于是有：
$G / G_{\mathrm{con}}$ 是离散的；
$G_{\mathrm{con}} / G_{\mathrm{sol}}$ 是若干个连通单李群直积的一个中心扩张；
$G_{\mathrm{sol}} / G_{\mathrm{nil}}$ 是阿贝尔的。一个连通阿贝尔李群同构于若干个 $\mathbb{R}$ 与圆群 $S^1$ 的直积；
$G_{\mathrm{nil}} / 1$ 是幂零的，因此其上升中心列的所有商群都是阿贝尔的。

　　这可以用来把关于李群的一些问题（例如寻找它们的酉表示）归结为连通单群、以及低维的幂零与可解子群的相应问题。

　　此外：

李群的微分同胚群在该李群上是可迁作用的；
每个李群都是可平行化流形，因此是可定向流形（其切丛与自身与单位元处切空间的乘积之间存在丛同构）。

8. 无限维李群

　　李群通常被定义为有限维的，但也存在许多与李群类似、只是维度为无限的群。定义无限维李群的最简单方式，是在局部上以 Banach 空间为模型（有限维情形中使用的是欧几里得空间）。在这种情形下，其基本理论与有限维李群的理论大体相似。

　　然而，这种方式对于很多应用来说并不充分，因为许多自然出现的无限维李群并不是 Banach 流形。为此，需要在更一般的局部凸拓扑向量空间上建模来定义李群。在这种情况下，李代数与李群之间的关系变得相当微妙，许多有限维李群中的结论不再成立。

　　在文献中，对于无限维群究竟具备哪些性质才能配得上 “李群” 这一前缀，并没有统一的术语标准。相比之下，李代数的情形要简单一些，因为 “李代数” 前缀的判定标准是纯粹代数性的。例如，一个无限维李代数可能有，也可能没有对应的李群。即便存在一个群与它对应，该群也可能不够 “良好” 而不能称为李群，或者该群与李代数之间的联系不够 “良好”（例如指数映射不能映射到单位元的某个邻域）。所谓 “良好”，在这里并没有一个普遍接受的定义。

　　已经被研究的一些例子包括：

流形的微分同胚群。关于圆的微分同胚群已经有相当多的研究结果。它的李代数大致是 Witt 代数，其中心扩张即 Virasoro 代数（参见从 Witt 代数导出 Virasoro 代数），而 Virasoro 代数正是二维共形场论的对称代数。更高维紧流形的微分同胚群是正规 Fréchet 李群；然而关于它们的结构，目前所知甚少。
时空的微分同胚群有时会出现在量子化引力的尝试中。
从流形到有限维李群的光滑映射群是规范群的一个例子（运算是逐点乘法），在量子场论和 Donaldson 理论中被使用。如果流形是圆，这类群被称为环群，它们有中心扩张，其李代数大致是 Kac–Moody 代数。
还有一些无限维推广，如一般线性群、正交群等。$^\text{[31]}$ 它们的重要方面之一是可能具有更简单的拓扑性质；例如参见 Kuiper 定理。在 M 理论中，一个 10 维的 $\mathrm{SU}(N)$ 规范理论在 $N \to \infty$ 时会变为 11 维理论。

9. 另见

李群的伴随表示
Haar 测度
齐性空间
李群主题列表
李群的表示
量子力学中的对称性
李点对称性（关于李群在微分方程研究中的应用）

10. 注释

说明性注释

　　
a.这是 “李群是一个形式李群” 的表述。关于后者的概念，参见 Bruhat。$^\text{[15]}$
b.Hall 只声称了光滑性，但相同的论证也能推出解析性。[需要引用]

引文

"What is a Lie group?". aimath.org. 检索于 2024 年 3 月 1 日。
Hawkins 2000，第 1 页
Hawkins 2000，第 2 页
Hawkins 2000，第 76 页
Tresse, Arthur (1893). "Sur les invariants différentiels des groupes continus de transformations". Acta Mathematica. 18: 1–88. doi:10.1007/bf02418270.
Hawkins 2000，第 43 页
Hawkins 2000，第 100 页
Borel 2001
Rossmann 2001，第 2 章
Hall 2015 推论 3.45
Hall 2015
Rossmann 2001
Stillwell 2008
Kobayashi & Oshima 2005，定义 5.3
Bruhat, F. (1958). "Lectures on Lie Groups and Representations of Locally Compact Groups" (PDF). Tata Institute of Fundamental Research, Bombay.
Helgason 1978，第 II 章，第 2 节，命题 2.7
Hall 2015 定理 3.20
另见 Hall 2015，命题 3.30 以及第 3 章练习 8
Hall 2015 推论 3.50
Hall 2015 定理 5.20
Hall 2015 例子 3.27
Hall 2015 第 1.3.4 节
Hall 2015 推论 5.7
Hall 2015 定理 5.6
Hall 2015 第 13.2 节
Hall 2015 定理 3.42
"Introduction to Lie groups and algebras: Definitions, examples and problems" (PDF). State University of New York at Stony Brook. 2006. 原始 PDF 存档于 2011 年 9 月 28 日. 检索于 2014 年 10 月 11 日。
Hall 2015 定理 5.20
Hall 2015 第 III 部分
Helgason 1978，第 131 页
De Kerf, E.A.; Bäuerle, G.G.A.; Ten Kroode, A.P.E., 编 (1997). "Lie algebras of infinite matrices". Lie Algebras - Finite and Infinite Dimensional Lie Algebras and Applications in Physics. Studies in Mathematical Physics. 第 7 卷. 页 305–364. doi:10.1016/S0925-8582(97)80009-7. ISBN 978-0-444-82836-1.

11. 参考文献

Adams, John Frank (1969), Lectures on Lie Groups, Chicago Lectures in Mathematics, 芝加哥: Univ. of Chicago Press, ISBN 978-0-226-00527-0, MR 0252560.
Borel, Armand (2001), Essays in the history of Lie groups and algebraic groups, History of Mathematics, 第 21 卷, 普罗维登斯, 罗德岛: American Mathematical Society, ISBN 978-0-8218-0288-5, MR 1847105.
Bourbaki, Nicolas, Elements of mathematics: Lie groups and Lie algebras. 第 1–3 章 ISBN 3-540-64242-0, 第 4–6 章 ISBN 3-540-42650-7, 第 7–9 章 ISBN 3-540-43405-4.
Chevalley, Claude (1946), Theory of Lie groups, 普林斯顿: Princeton University Press, ISBN 978-0-691-04990-8. Cohn, Paul Moritz (1957). Lie Groups. Cambridge Tracts in Mathematical Physics. Cambridge University Press. OCLC 529830.
Coolidge, Julian Lowell (2003). A History of Geometrical Methods. Dover Publications. pp. 304–317. ISBN 978-0-486-49524-8.
Fulton, William; Harris, Joe (1991). Representation theory. A first course. Graduate Texts in Mathematics, Readings in Mathematics. 第 129 卷. 纽约: Springer-Verlag. doi:10.1007/978-1-4612-0979-9. ISBN 978-0-387-97495-8. MR 1153249. OCLC 246650103.
Gilmore, Robert (2008). Lie groups, physics, and geometry: an introduction for physicists, engineers and chemists. Cambridge University Press. doi:10.1017/CBO9780511791390. ISBN 978-0-521-88400-6.
Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Graduate Texts in Mathematics, 第 222 卷 (第 2 版), Springer, doi:10.1007/978-3-319-13467-3, ISBN 978-3319134666.
Harvey, F. Reese (1990). Spinors and calibrations. Academic Press. ISBN 0-12-329650-1.
Hawkins, Thomas (2000), Emergence of the theory of Lie groups, Sources and Studies in the History of Mathematics and Physical Sciences, 柏林, 纽约: Springer-Verlag, doi:10.1007/978-1-4612-1202-7, ISBN 978-0-387-98963-1, MR 1771134（Borel 的书评）。
Helgason, Sigurdur (1978). *Differential Geometry, Lie Groups, and Symmetric Spaces*. 纽约: Academic Press. p. 131. ISBN 978-0-12-338460-7.
Knapp, Anthony W. (2002), *Lie Groups Beyond an Introduction*, Progress in Mathematics, 第 140 卷 (第 2 版), 波士顿: Birkhäuser, ISBN 978-0-8176-4259-4.
Kobayashi, Toshiyuki; Oshima, Toshio. (2005), Lie Groups and Representation Theory（日文）, 岩波书店, ISBN 4-00-006142-9.
Lie, Sophus (1876), "Theorie der Transformations-Gruppen (I, II)", Archiv for Mathematik og Naturvidenskab, 1: 19–57, 152–193.
Nijenhuis, Albert (1959). "Review: Lie groups, by P. M. Cohn". Bulletin of the American Mathematical Society. 65 (6): 338–341. doi:10.1090/s0002-9904-1959-10358-x.
Rossmann, Wulf (2001), Lie Groups: An Introduction Through Linear Groups, Oxford Graduate Texts in Mathematics, 牛津大学出版社, ISBN 978-0-19-859683-7.（2003 年重印版更正了若干印刷错误。）
Sattinger, David H.; Weaver, O. L. (1986). Lie groups and algebras with applications to physics, geometry, and mechanics. Springer-Verlag. doi:10.1007/978-1-4757-1910-9. ISBN 978-3-540-96240-3. MR 0835009.
Serre, Jean-Pierre (1965), *Lie Algebras and Lie Groups: 1964 Lectures given at Harvard University*, Lecture notes in mathematics, 第 1500 卷, Springer, ISBN 978-3-540-55008-2.
Steeb, Willi-Hans (2007), *Continuous Symmetries, Lie algebras, Differential Equations and Computer Algebra: second edition*, World Scientific Publishing, doi:10.1142/6515, ISBN 978-981-270-809-0, MR 2382250.
Stillwell, John (2008). Naive Lie Theory. Undergraduate Texts in Mathematics. Springer. doi:10.1007/978-0-387-78214-0. ISBN 978-0387782140.
Warner, Frank W. (1983), Foundations of Differentiable Manifolds and Lie Groups, Graduate Texts in Mathematics, 第 94 卷, 纽约柏林海德堡: Springer-Verlag, doi:10.1007/978-1-4757-1799-0, ISBN 978-0-387-90894-6, MR 0722297.
Ziller, Wolfgang (2010). "Lie Groups. Representation Theory and Symmetric Spaces" (PDF). 宾夕法尼亚大学.

12. 外部链接

维基共享资源中的李群相关媒体
Journal of Lie Theory（《李理论期刊》）

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。