接收者操作特征曲线

贡献者： xzllxls

　　 接收者操作特征曲线（Receiver operating characteristic curve, ROC）是一种用于评价二分类器的分类性能的图表。该方法来源于信号检测论，是在第二次世界大战中，由电子信号工程师发明的。在心理学领域中也有广泛应用。

　　 接收者操作特征曲线能够评估分类模型在不同阈值下的性能，通过绘制真阳性率（True positive rate, TPR）与假阳性率（False positive rate, FPR）的关系来衡量模型的区分能力。

　　 曲线中点的坐标是真阳率和假阳率。随着分类器阈值的变化，真阳率和假阳率分别随之改变，由此产生一系列的点，然后将相邻两点连接起来，即构成接收者操作特征曲线。

　　 图 1 中蓝色曲线即为 ROC 曲线。横坐标为假阳率，纵坐标为真阳率。红色对角线表示一个完全随机分类器的 ROC 曲线。如果一个分类器的 ROC 曲线大体在红色虚线的上方，则表示性能优于随机分类器。

　　 ROC 曲线分析可以帮助我们做模型选择，选择最优模型，抛弃次优模型。曲线下面积（Aera under curve, AUC）是 ROC 曲线最基本的评估指标，能表示分类器预测能力的一项常用的统计值。顾名思义，表示的是曲线下方，横轴上方的面积。通常把整图的面积定义为 1，则 AUC 的值在 $0$ 和 $1$ 之间。该面积值越大，则表示分类模型效果越好；反之，则越差。因此，定性地讲，ROC 曲线越靠近左上方，ROC 曲线下的面积越大，代表模型的效益越高。

• 当 AUC = 1 时，代表分类器非常完美，但这毕竟是理想状况。
• 当 AUC > 0.5 时，代表分类器分类效果优于随机猜测，模型有预测价值。
• 当 AUC = 0.5 时，代表分类器分类效果与随机猜测相同，模型无预测价值。
• 当 AUC < 0.5 时，代表分类器分类效果比随机猜测差，但如果进行反预测，就会优于随机猜测。

1. 编程实战

　　 以下给出一个用 Python 语言产生接受者操作特征曲线，并计算曲线下面积的示例程序。该程序用 scikit-learn 机器学习库来求接受者操作特征曲线和曲线下面积。然后利用 matplotlib 库来绘制图形。采用 numpy 库来表示数据。

代码示例

from sklearn.metrics import roc_curve
from sklearn.metrics._ranking import auc

import matplotlib.pyplot as plt
import numpy as np


# 每个样本的实际的标签值
y = np.array([0, 1, 0, 1, 0, 0, 1, 1]) 

# 分类模型输出的分数值
scores = np.array([-0.20, -1.54, -1.38, -1.63, -1.70, -2.41, -1.14, -0.79])

# 计算真阳性率和假阳性率
fpr, tpr, thresholds = roc_curve(y, scores, pos_label=1)

# 计算曲线下面积
roc_auc = auc(fpr, tpr)

# 绘制接受者操作特征曲线
plt.title('ROC')
plt.plot(fpr, tpr, 'b', label="AUC=" + str(roc_auc))
plt.legend(loc='lower right')
plt.plot([0, 1], [0, 1], 'r--')
plt.ylabel('TPR')
plt.xlabel('FPR')
plt.show()

结果与说明

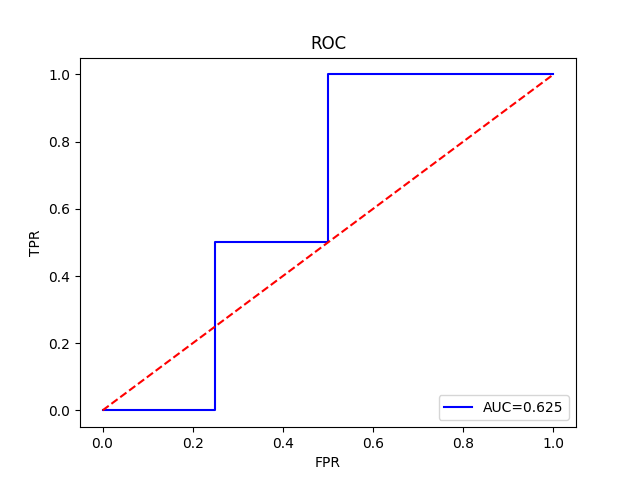
　　 执行上述程序，产生的图如下：

　　 图 2 中的横坐标表示假阳性率，纵坐标表示真阳性率。蓝色曲线即是 ROC 曲线，红色虚线为对角线。右下方显示的是 AUC 曲线下面积，值为 0.625，表示该分类模型的预测能力优于随机猜测。