最小生成树

贡献者： 有机物

　　 生成树的定义：是指在一个带权的无向联通图中选择 $n$ 个点和 $n - 1$ 条边构成的无向联通子图。

　　 最小生成树的定义即为边权最小的生成树。

　　 求最小生成树最常用的两种算法为：Prim 和 Kruskal。Prim 常用于稠密图，Kruskal 则相反。

1. Prim 算法

　　 Prim 算法的思路与 Dijkstra 算法非常相似。 定义 $S$ 为当前已经确定了属于最小生成树的结点，$T$ 为集合外的结点。使用 dist 数组存储每个结点到 $S$ 集合的距离，距离定义为如果有多个结点指向 $S$ 集合，则距离最短的边为这个结点到 $S$ 集合的距离。最开始初始化所有结点到 $S$ 集合的距离为 $+\infty$，$1$ 号点到 $S$ 集合的距离为 $0$。一共进行 $n$ 次迭代，每次找到 $T$ 集合中距离 $S$ 集合距离最短的结点 $t$，然后用 $t$ 结点更新其他点（与 $t$ 相连的结点）到 $S$ 集合的距离，然后把 $t$ 从 $T$ 集合中删去，加入到 $S$ 集合中，则 $t$ 结点为当前已经确定了属于最小生成树的结点。

　　 具体的做法是用一个布尔数组来标记一个点是否属于 $S$ 集合，st[i] 为 true 则结点 $i$ 属于 $S$ 集合，反之不属于。每次从未标记的结点中选择一个 dist 值最小的结点，把这个结点加入到 $S$ 集合中，并把这个结点的权值加到答案里，然后更新所有出边。

　　 朴素 Prim 的时间复杂度为：$\mathcal{O}(n^2)$，使用堆优化可以达到 $\mathcal{O}(m \log_2 n)$，但是使用堆优化的 Prim 算法代码太长，不如直接用 Kruskal。

Prim 算法的正确性证明

　　 使用数学归纳法证明：

　　 证明对于 $\forall k < n$，存在一棵最小生成树包含算法前 $k$ 选择的不在 $S$ 集合且距离最近的边。

　　 初始 $k = 1$，存在一棵最小生成树数包含第一步选择的最短的边，证明显然成立。

　　 假设算法前 $k$ 步选择的边能包含在最小生成树中，那么第 $k + 1$ 步选择的边也包含在最小生成树中。

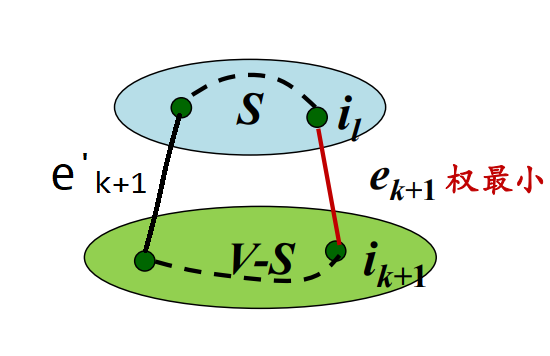
　　 第 $k + 1$ 步算法选择的边为 $e_{k + 1}$，并且权值最小。同样用反证法证明，假设没有选择 $e_{k + 1}$ 这条边，选择了另一条 $e_{k + 1}'$ 这条边，如果把 $e_{k + 1}$ 选择上，会构成一条回路，但如果把 $e_{k + 1}'$ 删去，构成了一棵树，并且总权值之和不会变大。

　　 所以算法第 $k+1$ 步仍可得到最小生成树.

const int N = 510, M = 1e5 + 10, INF = 0x3f3f3f3f;
int n, m, dist[M], st[M], g[N][N];  // g 数组用邻接矩阵存储图

int prim()
{
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    int res = 0;
    for (int i = 0; i < n; i ++ )
    {
        int t = -1; // t 表示不在 S 集合中距离 S 集合距离最短的结点，-1 表示还没找到
        for (int j = 1; j <= n; j ++ )
            if (!st[j] && (t == -1 || dist[j] < dist[t]))  
                t = j;  
        
        st[t] = true;
        if (dist[t] == INF) return INF; // 找到一个点与图是不联通的
        res += dist[t]; // 这个结点到 S 集合的边权为答案
        
        for (int j = 1; j <= n; j ++ )
            dist[j] = min(dist[j], g[t][j]); // 用 t 更新其他点的距离
    }
     
    return res;
}

2. Kruskal 算法

　　 Kruskal 算法的思想较为简单，思想是基于贪心算法。具体做法是：把每条边的权值从小到大排序，然后依次枚举每条边 $(a,b,w)$，如果 $a$ 和 $b$ 不联通，就合并这两个点所在的集合，并把答案加上这条边的权值，不连通就忽略这条边。初始化每个结点都是一个集合。维护不相交森林可以用并查集，该算法的时间复杂度的瓶颈在排序上，所有 Kruskal 的时间复杂度为 $\mathcal{O}(m \log_2 m)$。最后如果最小生成树中加的边的个数小于 $n - 1$，则最小生成树构建失败。

int n, m, p[N];
struct Node
{
    int a, b, c;
}e[M];

int find(int x)  // 并查集
{
    p[x] = p[x] != x ? find(p[x]) : p[x];
}

int kruskal()
{
    sort(e, e + m, [&](Node &a, Node &b) {  // 将每条边的权值从小到大排序，这里使用了 Lambda
        return a.c < b.c;
    });
    
    int res = 0, cnt = 0;
    for (int i = 0; i < m; i ++ )
    {
        int a = e[i].a, b = e[i].b, c = e[i].c;
        a = find(a), b = find(b);
        if (a != b)  // 如果 a b 不连通
        {
            p[a] = b;
            res += c;
            cnt ++ ;
        }
    }
    
    if (cnt < n - 1) return INT_MAX;
    return res;
}