并查集

贡献者： 有机物

　　¹并查集（disjoint-set）是一个树形、用于维护不相交的集合的数据结构。

　　 对于并查集，主要有如下操作：

1. $\mathtt{merge}$ 合并两个集合；(“并”）
2. $\mathtt{find}$ 判断两个元素是否属于同一个集合。（“查”）

　　 定义集合的表示方法：“代表元” 法，即每个集合都会选择一个固定的元素，作为这个集合的代表。其次需要定义归属关系的表示方法：使用一个树形结构存储每个集合，树上的每个结点都是一个元素，树根是集合的代表元素。我们用 p[i] 表示每个结点的父结点，初始化 p[i] 都指向自己，树根也指向自己。在合并两个集合时，只需要将其中一个树根的父结点指向另一个树根，即 p[root_1] = root_2。在查询每个集合的树根时，朴素的办法就是通过 p[i] 存储的值不断递归访问父结点，直至到达树根。为了提高效率，我们引入了路径压缩这种优化方法。

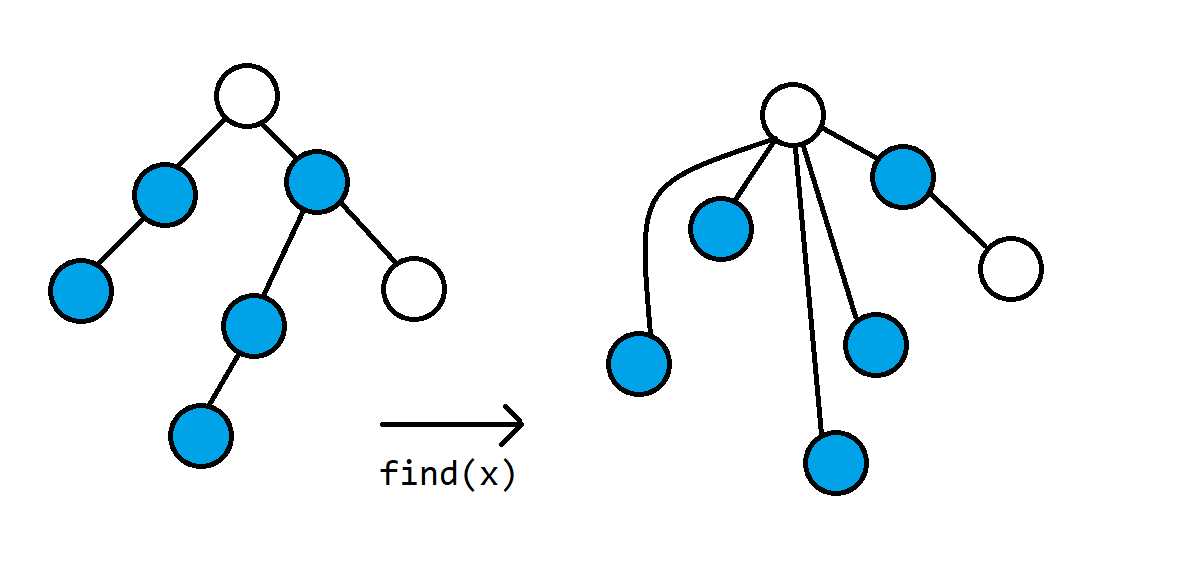
　　 在进行合并和查询的操作中，我们只关心每个集合的根结点，所以我们在 $\mathtt{find}$ 操作的时候，把访问过的每个结点都直接指向树根，这种优化方法被称为路径压缩，进行完路径压缩之后，每个结点的父结点都为根结点了。加上路径压缩的并查集每次 $\mathtt{find}$ 的操作均摊时间复杂度为 $O(\log N)$。

　　 还有一种优化方法为按秩合并，单独采用 “按秩合并” 的并查集每次 $\mathtt{find}$ 的操作均摊时间复杂度也为 $O(\log N)$，若同时采用 “路径压缩” 和 “按秩合并” 的并查集，每次 $\mathtt{find}$ 的操作均摊时间复杂度为 $O(\alpha(N))$，其中 $\alpha(N)$ 为反阿克曼函数，对于 $\forall \ N \leq 2^{2^{10^{19729}}}$，都有 $\alpha(N) < 5$。

　　 并查集的存储： int p[N]

　　 并查集的初始化： 起初所以元素各自构成一个独立的集合，即有 $n$ 棵 $1$ 个点的树。

for (int i = 1; i <= n; i ++ ) p[i] = i;

　　 并查集的 $\mathtt{find}$ 操作：

// 返回 x 的根结点 + 路径压缩
int find(int x)
{
    // 每个集合中只有根结点的 p[x] 值等于他自己
    if (p[x] != x) p[x] = find(p[x]); // 如果 x 不是根结点，那么就让 x 的父结点直接等于根结点
    return p[x];
}

// 熟练之后可以写成一行：
// return p[x] = (p[x] != x ? find(p[x]) : p[x]);

　　 并查集的 $\mathtt{merge}$ 操作：

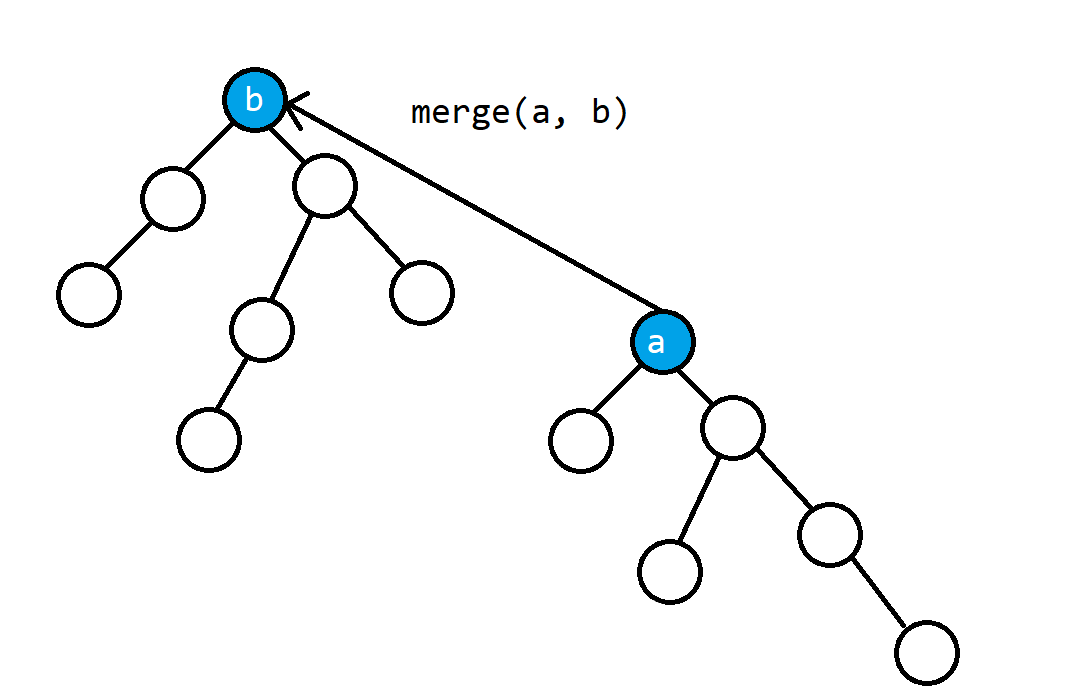
// 合并 x 和 y 的所在集合，等于让其中一个集合的父结点指向另一个集合的根结点
void merge(int x, int y)
{
    p[find(x)] = find(y);
}

　　 如果想维护集合的大小呢？可以开一个 cnt 数组用于维护集合的大小，最初每个集合的大小初始化为 $1$。

　　 在 $\mathtt{merge}$ 操作的函数多加一句语句：cnt[b] += cnt[a];，加之前需要判断 $a$ 和 $b$ 是不是不在一个集合内，以免重复加导致答案不对。

　　 以上就是并查集的基本操作了。

1. ^ 参考 Wikipedia 相关页面。