多项式插值 2

贡献者： ditto; int256; addis

1. 什么是插值

　　 插值法，就是在函数表达式未知的情况下，通过已知点处的函数值来估计未知点处函数值的方法。

　　 插值法是数值计算中一种常用且基础的方法，在数据挖掘、数学建模等诸多领域都有广泛的应用。

2. 多项式插值

　　 当式 2 中的简单函数 $p(x)$ 是多项式函数时，该插值方法就叫多项式插值，$p(x)$ 被称为插值多项式。当有 $n$ 个插值点时，插值多项式的次数一定小于等于 $n$ 次。

　　 证明： 由 Vandermonde 矩阵为非奇异矩阵易证。

　　 由 定理 1 可知，对一组给定的插值点以及对应的函数值，由插值法得到的多项式存在且唯一。因此，下面介绍的两种插值方法只是推导不同，但其最终得到的插值多项式是一致的。

Lagrange 插值

　　 根据定义，由构造法易得：

Lagrange 插值的 MATLAB 实现

　　 这里以 $y = \frac{1}{1+x^2}$ 在 $[-5,5]$ 的 n 次 Lagrange 插值函数为例展示 Lagrange 插值的具体实现。

function f = LagrangeIP(n)
%   [-5,5]内的Lagrange等距点插值，多项式次数为n,插值函数为y = 1./(1+x.*x);
x = -5:0.1:5;
y = 1./(1+x.*x);
x1 = linspace(-5,5,n+1);%插值节点
y1 = 1./(1+x1.*x1);
f = 0;%f为插值形成的函数
for i = 1:n+1
    L = 1;%L为插值基函数
    for j = 1:n+1
        if j~=i
            L = L.*(x-x1(j))./(x1(i)-x1(j));
        end
    end
    L = y1(i).*L;
    f = f+L;
end
plot(x,f,x,y);

Newton 插值

Runge 现象

　　 如果想要使得在取无限密的等分点时，拉格朗日插值得到的函数能够最终趋于原函数，拉格朗日插值要求函数不仅仅在这插值范围内解析，还要求在复数域上解析，否则在函数边界就会出现Runge 现象（龙格现象）。解决这个问题的方法是不采用等间隔插值点，而是其他取点方法，例如切比雪夫点。

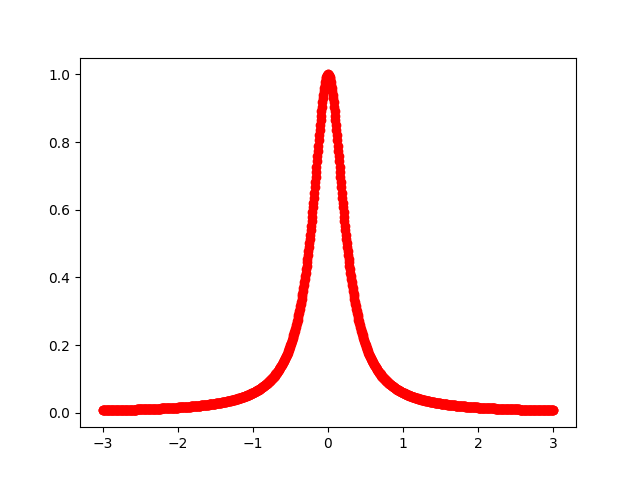
　　 以函数 $$y = f(x) = \frac1{1+16 x^2} ~,$$ 举例，该函数本身图像为：

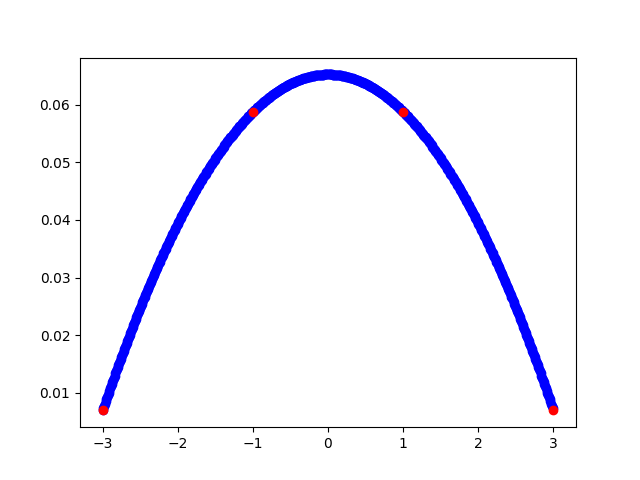
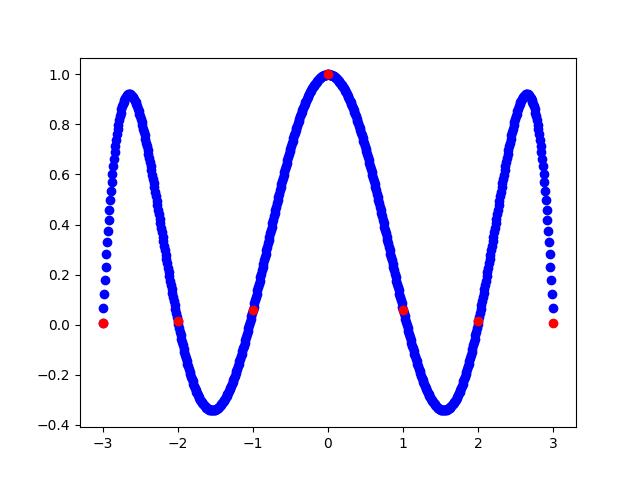
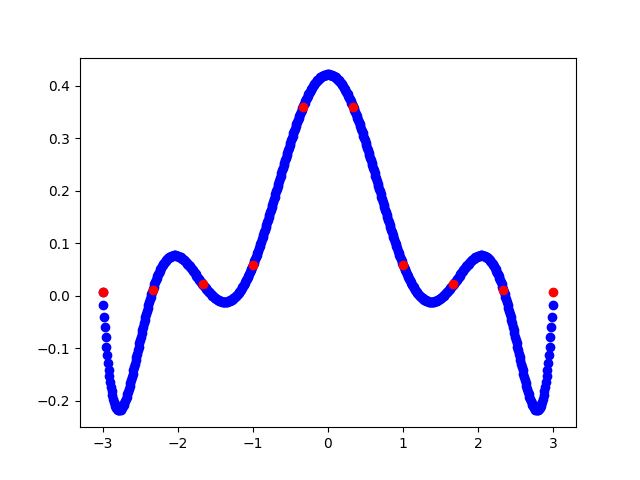
　　 在其中等间隔取点，随着点数的变多，插值函数在边缘的 “抖动” 越来越剧烈，如下图：

　　 这现象便是龙格现象，原因是刚才提到的，该函数在插值区间附近的复数域不解析。生成这图像使用的是 python 的 matplotlib 库，代码如下：

import numpy as np
from tqdm import tqdm
from sympy import Symbol as symSym
from sympy import Poly as symPoly
from sympy import expand as polyExpand
from matplotlib import pyplot as plt



class LagrangeInter:
    def __init__(self, xs: [list, np.array], ys: [list, np.array]):
        self.x = np.asarray(xs, dtype=np.float64)
        self.y = np.asarray(ys, dtype=np.float64)
        
        if len(self.x) > 1:
            if len(self.x) == len(self.y):
                self.n = len(self.x)
            else:
                raise Exception("不能对空点集进行 Lagrange 插值")
        else:
            raise Exception("x, y 数量不对应")
        
        self.poly = None
        self.polyCoff = None
        self.coffOrder = None
    
    def interp(self):
        t = symSym("t")
        self.poly = 0
        for i in tqdm(range(self.n)):
            basis_fun = self.y[i]
            for j in range(0, i):
                basis_fun *= (t - self.x[j]) / (self.x[i] - self.x[j])
            for j in range(i + 1, self.n):
                basis_fun *= (t - self.x[j]) / (self.x[i] - self.x[j])
            self.poly += basis_fun
            self.poly = polyExpand(self.poly)
            poly = symPoly(self.poly, t)
            self.polyCoff = poly.coeffs()
            self.coffOrder = poly.monoms()
    
    def calc(self, x0: [list, np.array]):
        x0 = np.asarray(x0, dtype=np.float64)
        y0 = np.zeros(len(x0))
        t = self.poly.free_symbols.pop()
        
        for i in tqdm(range(len(x0))):
            y0[i] = self.poly.evalf(subs={t: x0[i]})
        return y0



def func(x: float) -> float:
    return 1/(1+ 16*x*x)



if __name__ == "__main__":
    a = np.linspace(-3, 3, 10, endpoint=True)# 将这行的 10 替换成插值多项式的选点数量（即阶数）
    b = [func(x) for x in a]
    x0 = np.arange(-3, 3, 0.01)
    lagInterp = LagrangeInter(a, b)
    lagInterp.interp()
    y0 = lagInterp.calc(x0)
    plt.plot(x0, y0, 'bo')
    plt.plot(a, b, 'ro')
    plt.show()