贡献者: yhgao
1. 等离子体的基本概念:粒子的集体行为
等离子体作为区别于固体、液体、气体而独立的物质第四态,其最大的特性就是内部相互作用力的改变——从固液气中的中性成分作用力占主导变为了电磁相互作用力占主导。等离子体由电子和离子组成,这些带电的粒子所携带的总电荷相等,也就是说体系整体上呈现电中性。等离子体中可以有中性成分吗?当然是可以的,但是考虑到 “库仑力主导” 的原则,电的作用要占到主导地位才能称得上等离子体,也就是说带电粒子占比要足够高或者说电离度足够高。
为了进一步地说明,我们不妨考察一个基本的物态相变的例子:对于某一固体,随着温度的升高,其内部分子的振动能量增加,原本的小尺度振荡被破坏,固体变成了可以自由流动变形的液体。液体在分子作用力作用下,其内部分子能被限制在一定体积中而不能随意逃离;但进一步加热液体,分子做热运动的动能进一步增大,突破分子作用力的限制而可以自由在空间中运动,这就成为了气体。不过这时,气体中的主导相互作用仍为分子或原子间的相互碰撞这样的中性作用。我们再对气体进一步加热,当其热运动的动能增加到其组分的第一电离能时,碰撞就能导致原子或分子的电离,产生正离子和电子。这一过程也就是电离过程,而电离成分数密度与发生电离前中性成分数密度之比就是电离度。这是的气体可以称为部分电离的气体,如果温度进一步升高,电离度会随之增加,当库伦相互作用占绝对主导地位时,等离子态就出现了。
等离子体看上去只是强烈电离的气体,但是其物理性质却和气体截然不同,其最大的特点就是 “牵一发而动全身”,库伦相互作用使原本过于松散随意的气体粒子变得更加循规蹈矩,也在它们之间建立了更加密切的联系,从而表现出一种集体行为。更准确来说,集体行为是指等离子体中的任一带电粒子行为,都不仅取决于该粒子所在位置的局部条件,而更多取决于远距离区域的等离子体状态。
综合以上,我们可以给出等离子体的定义如下:
等离子体是带电粒子和中性粒子组成的表现出集体行为的一种准中性气体。
接下来我们来展现这种集体行为的几个例子,并对准中性加以进一步的说明。
等离子体振荡
等离子体集体行为的第一个例子就是等离子体振荡。考虑振荡和波动,通常要明确两点——初始扰动和回复力。对等离子体来说,回复力通常是各种电磁力;对于这里讨论的基本的等离子振荡,回复力就是库仑力或者说静电力。我们要施加的初始扰动则是把等离子体中的一部分负电荷(一般为电子)挪离静电平衡位置,正电荷不动,然后我们来考虑系统在静电回复力下的振荡。
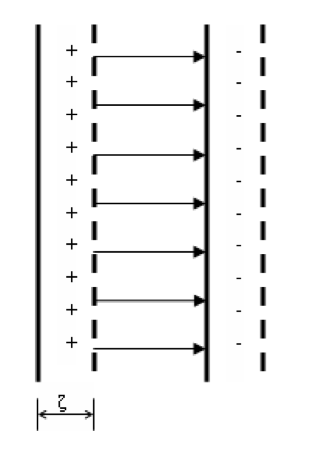
图 1:等离子体振荡示意图
为简单起见,我们把问题抽象成这样的模型。初始时等离子体位于一个 “等离子体平板”(即图中实线区域内)中保持平衡状态,由数密度相等的电子和质子构成,即有
\begin{align}
n_e=n_p=n_0~.
\end{align}
将其中的电子均匀向右移动一个小距离 $\xi$ 到
图 1 中虚线位置,两端就会形成正负电荷区,从而产生电场。由于 $\xi$ 很小,两端的正负电荷区可以看成带点平面,整个结构类似于一个平行板电容器,板上的面电荷密度为
\begin{align}
\sigma=en_0V/S=en_0\xi~,
\end{align}
从而中间部分的电场为
\begin{align}
E=\frac{\sigma}{\varepsilon_0}=\frac{en_0\xi}{\varepsilon_0}~.
\end{align}
电场力提供了 “拉回” 电子的回复力,则有
$m_e\ddot{\xi}=-eE=\frac{n_0e^2}{\varepsilon_0}\xi~,$
即
\begin{align}
\ddot{\xi}+\frac{n_0e^2}{m_e\varepsilon_0}\xi=0~.
\end{align}
从而得到电子的振荡频率
\begin{equation}
\boxed{\omega_p^2=\frac{n_0e^2}{m_e\varepsilon_0}}~.
\end{equation}
这一振荡最先由 Langmiur 发现,因此称为
Langmiur 振荡,这一频率也称为
Langmiur 频率。我们可以再从物理上理解一下电子的振荡过程,电子先在向右的电场的作用下向左运动,回到原位之后继续向左,电子和离子交换相对位置,电场方向就会反向,电子开始受向右的力。这样循环往复的过程就是等离子的 Langmiur 振荡。
将此结果稍作推广,对于密度、质量、电荷数为 $(n_i,m_i,Z)~$ 的离子,其相应振荡频率为
\begin{equation}
\omega_{pi}^2=\frac{n_i Z^2e^2}{m_i\varepsilon_0}~.
\end{equation}
由于离子的质量远远大于电子质量,离子的振荡频率远远小于电子振荡频率。
德拜屏蔽
集体行为的另一表现是德拜屏蔽。考虑在等离子体中放入一个试验电荷 $q$,其库伦场会吸引周围异号电荷、排斥同号电荷,最终形成对此试验电荷电场的屏蔽,在离试验电荷一定距离之外的电荷会无法感受到 $q$ 的存在。这一屏蔽效应就称为德拜屏蔽(Debye shielding),而有效屏蔽的距离则称为德拜半径或德拜长度,这一距离所确定的空间范围称为德拜球。
下面具体推导德拜半径的表达式。
初始时等离子体的电子和离子密度应满足
\begin{equation}
\sum_i Z_i n_{i0}=n_{e0}~.
\end{equation}
当试验电荷 $q$ 以外的电荷重新分布产生屏蔽效应时,应当满足热平衡。设这时的电势(称为
德拜势)为 $\phi(r)$,考虑离 $q$ 距离为 $r$ 和 $r+\mathrm{d} r$ 的两个球面,则两球面间隔内电子气体压力和电场力应平衡,而压力为 $S\mathrm{d}P=S\mathrm{d}(n_ekT)=SkT\mathrm{d}n_e$,电场力为 $\int_r^{r+\mathrm{d}r} eE(r)n_eS\mathrm{d}r=en_eS\int_r^{r+\mathrm{d}r}E(r)\mathrm{d}r=en_eS\mathrm{d}\phi(r)$,故有
\begin{equation}
kT\mathrm{d}n_e=en_e\mathrm{d}\phi(r)~.
\end{equation}
可解出电子数密度 $n$ 满足
\begin{equation}
n_e(r)=n_{e0}\exp{\left( \frac{e\phi(r)}{kT}\right)}~.
\end{equation}
此即玻尔兹曼分布公式,其中 $n_e0$ 为电势 $\phi=0$ 时(即初始时)的电子密度。由于离子质量较大,可以暂不考虑离子分布的变化,即假设 $n_i=n_{i0}$。
把等离子体视为理想气体(事实上,前面的推导中我们已经用到了理想气体状态公式),则电荷间的电势能远远小于电荷热运动的能量,即可以假设 $e\phi(r)\ll kT$(等离子体的温度一般比较高,而电势只要不离 $q$ 很近都可以认为比较小,所以一般来说这样的假设是合理的),则 $n_e(r)=n_{e0}(1+\frac{e\phi(r)}{kT})$。
这时的等离子体总电菏为
\begin{equation}
\begin{aligned}
Q&=q\delta(r)-n_e(r)e+\sum_{i} Z_i n_{i}(r)e\\
&=q\delta(r)-n_{e0}(1+\frac{e\phi(r)}{kT})e+n_{e0}e\\
&=q\delta(r)-\frac{n_{e0}e^2\phi(r)}{kT}~,
\end{aligned}
\end{equation}
代入泊松方程 $\nabla^2\phi=-Q/\varepsilon_0$ 得到
\begin{equation}
\left(\nabla^2-\frac{1}{\lambda_D^2} \right) \phi(r)=-\frac{q\delta(r)}{\varepsilon_0}~,
\end{equation}
其中
\begin{equation}
\boxed{\lambda_D^2=\frac{kT\varepsilon_0}{n_{e0}e^2}}~.
\end{equation}
下面考虑如何求解方程(1.11),首先有 $\nabla^2\phi(r)=\frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2\frac{\partial\phi}{\partial r}\right)$。令 $\phi(r)=u(r)/r$,在 $r=0$ 之外,方程(1.11)化为
\begin{equation}
\begin{aligned}
0&=\nabla^2\phi(r)-\frac{1}{\lambda_D^2}\phi(r)\\
&=\frac{1}{r^2}\frac{\partial}{\partial r}\left[r^2\frac{\partial(u(r)/r)}{\partial r}\right]-\frac{1}{\lambda_D^2}\frac{u(r)}{r}\\
&=\frac{1}{r^2}\frac{\partial}{\partial r}\left[r^2\left(-\frac{1}{r^2}u(r)+\frac{1}{r}\frac{\partial u(r)}{\partial r}\right)\right]-\frac{1}{\lambda_D^2}\frac{u(r)}{r}\\
&=\frac{1}{r^2}\frac{\partial}{\partial r}\left(-u(r)+r\frac{\partial u(r)}{\partial r}\right)-\frac{1}{\lambda_D^2}\frac{u(r)}{r}\\
&=\frac{1}{r^2}\left(-\frac{\partial u}{\partial r}+\frac{\partial u}{\partial r}+r\frac{\partial^2 u}{\partial r^2}\right)-\frac{1}{\lambda_D^2}\frac{u(r)}{r}\\
&=\frac{1}{r}\left(\frac{\partial^2 u}{\partial r^2}-\frac{u}{\lambda_D^2}\right)~,
\end{aligned}
\end{equation}
即 $\frac{\partial^2 u}{\partial r^2}=\frac{u}{\lambda_D^2}$ 其解为 $u=C_1 e^{-r/\lambda_D}+C_2 e^{r/\lambda_D}$。考虑到电势应随 r 增大而减小,故不考虑第二项 $C_2 e^{r/\lambda_D}$,从而 $\phi(r)=\frac{C_1}{r}e^{-r/\lambda_D}$。此外,当 $r\to 0$ 时,德拜势应当回到静电势的表达式,故 $C_1=\frac{q}{4\pi \varepsilon_0}$。综合以上,我们得到
\begin{equation}
\boxed{\phi(r)=\frac{q}{4\pi \varepsilon_0 r}e^{-r/\lambda_D}~.}
\end{equation}
容易检验(方法可参考郭鸿硕《电动力学》p190-191),上式为方程(1.11)的解,也就是德拜势的表达式。
从(1.14)式可见,德拜势就是将屏蔽前的静电势乘上一个衰减指数项。物理学上一般认为,衰减到原来的 1/e 之后,就不再考虑这一物理量。所以当 $r>\lambda_D$ 之后,就可以不考虑 $q$ 所产生的库伦相互作用,所以 $\lambda_D$ 就是屏蔽半径,也就是德拜半径,其表达式已由(1.12)式给出。进而我们有德拜球的体积为 $\frac{4\pi}{3}\lambda_D^3$,德拜球中的粒子数目为
\begin{equation}
\boxed{\varLambda=\frac{4\pi}{3}n\lambda_D^3=1380T^{3/2}/n^{1/2}~.}
\end{equation}
该参数被称为
等离子体参数。显然,如果带电粒子不足够多就无法实现对试验电荷电场的有效屏蔽,因此应有 $\varLambda\gg 1$。所以,德拜屏蔽也是一种等离子体的集体行为。
等离子体的准中性与响应时间
德拜屏蔽意味着等离子体可对任一点和或有关的扰动电场在一定空间和时间尺度上实现屏蔽,这就使得等离子在更大的时空尺度上表现出准中性(quasi-neutrality)。为什么说是 “准”?因为等离子体可以存在微小的电荷涨落,“中性” 并不需要严格意义上成立,前面的(1.7)式可以改写为
\begin{equation}
\sum_i Z_in_{i}\approx n_e\gg \left|n_e-\sum_i Z_in_{i}\right|~.
\end{equation}
对于德拜屏蔽对于准中性的意义,可以再加以如下说明:向一开始完全电中性的等离子体中加一个试验电荷,电中性当然会被破坏,但是德拜屏蔽的存在使得破坏被局限在了德拜半径以内,因此只要等离子体的空间尺度足够大,就可以继续维持近似中性,也就是 “准中性”。这里我们看到了对于等离子体空间尺度的一个限制,即 $L\gg \lambda_D$。
另一方面,等离子体要维持准中性,对时间尺度也有要求,也就是等离子体参数变化的特征时间 $T$ 应远大于所谓的
等离子体响应时间。等离子体响应时间是等离子体电荷以平均速度经过德拜半径长度所需的时间,用 $tau$ 表示。平均速度一般取为热速度 $V=\sqrt{\frac{kT}{m_e}}$,只考虑电子的运动,则有
\begin{equation}
\tau=\frac{\lambda_D}{V}=\sqrt{\frac{m_e\varepsilon_0}{n_{e0}e^2}}~.
\end{equation}
响应时间 $\tau$ 的意义可以理解为德拜屏蔽的实现时间,描述了等离子体对于电荷扰动的反应快慢。另一种理解是粒子经过德拜球的平均时间,这一时间要足够短才能使粒子受到德拜球内非电中性作用的时间可以忽略不计。
建立德拜屏蔽的过程其实也可看做施加扰动使等离子体偏离静电平衡状态,这自然也会引起等离子振荡。事实上,我们可以发现 Langmiur 频率与响应时间有如下关系:
\begin{equation}
\omega_p \tau=1~.
\end{equation}
这说明等离子体振荡、德拜屏蔽、准中性、等离子体响应等都是等离子体集体行为的不同侧面,之间有着密切的联系
2. 等离子体判据与碰撞频率
根据前面的讨论,我们已经可以提炼出等离子体所必须满足的一些条件:空间尺度 $L\gg \lambda_D$,时间尺度 $T\gg\tau$,等离子体参数 $\varLambda\gg1$。这里后两个条件其实有一定的等同性,从 $\varLambda$ 和 $\tau$ 的表达式来看,响应时间充分小和等离子参数充分大都要求粒子数密度足够大,所以可以只取 $\varLambda\gg1$ 作为一个判据。
除此以外,等离子体还应当满足带电粒子的相互作用远大于中性粒子所参与的相互作用,前者可以用等离子体振荡频率 $\omega_p$ 表示,后者则可用中性成分与带电粒子的碰撞频率 $\nu$ 来表示,也就是应有 $\omega_p\gg\nu$。
综合以上,可以得出三条等离子体判据:
\begin{equation}
L\gg \lambda_D~.
\end{equation}
\begin{equation}
\varLambda\gg1~.
\end{equation}
\begin{equation}
\omega_p\gg\nu~.
\end{equation}
3. 对等离子体的描述方法
要描述等离子体理论上只需要将电磁场方程组和每个电荷的运动方程联立求解,但是这往往过于复杂,粒子数目过多也使得这样求解并不现实。所以我们需要进行各种近似和简化,从而衍生出不同的描述方法。
单粒子轨道理论
单粒子轨道理论假设粒子的运动对场没有影响,只研究给定外场下粒子的运动情况,也不考虑粒子间的相互作用。这种描述方法只需要求解一个方程:
\begin{equation}
m\frac{d \boldsymbol{\mathbf{v}} }{dt}=q( \boldsymbol{\mathbf{E}} + \boldsymbol{\mathbf{v}} \times \boldsymbol{\mathbf{B}} )+ \boldsymbol{\mathbf{F}} ~.
\end{equation}
其中 $ \boldsymbol{\mathbf{F}} $ 是重力等可能的其他外力。这种方法只关注单个带电粒子在外场下的运动,不再考虑之前所述的集体行为,几乎已经不算是在研究等离子体了。但是单粒子轨道理论得出的很多结论对理解等离子体集体行为仍然是很有用的。
磁流体力学描述
磁流体力学(Magntohydrodynamics,MHD)采用流体力学的方法来研究等离子体,相当于在流体力学方程组里引入了电磁力,再与麦克斯韦方程组联立求解。流体力学的基本假设是 “连续介质假设”,等离子体要用流体力学的方法描述也要遵循这一假设,因此 MHD 适合描述大尺度、变化相对较慢的物理过程。对于比较稀薄或尺度较小的区域、一些边界层,MHD 可能不再适用,往往需要用下面所介绍的动理学描述(kenetic theory)。
动理学描述
与 MHD 主要处理流体的密度、速度、温度等宏观参量不同,动理论处理的是粒子的速度分布函数(veloci distri function,VDF)这一微观参量。VDF 是统计力学的概念,表示在某空间点、某速度取值范围内找到粒子的概率。动理学描述能让我们深入 “宏观充分小、微观充分大” 的流体质点内部,对粒子分布的微观行为进行更细致的研究。
动理论更接近等离子体运动的底层,相比 MHD 有更好的近似度;但是它还是只适合于小尺度的研究,在较的时间空间尺度中的计算就会太过复杂。因此 MHD 与动理学描述在等离子体物理学研究中处于同等重要的地位。
最后对动理学做一简单的说明:英文” kinetics” 过去被翻译为 “动力学”,但这容易与研究物体受力和运动变化规律的 “动力学(dynamics)” 混淆,所以现其现定名为 “动理学”,专指研究稀薄流体微观粒子(或准粒子)运动机理的学科。苏联著名的《理论物理学教程》第十卷就名为《物理动理学》。
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。