2017 年考研数学试题（数学一）

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 选择题

　　 1.若函数 $f(x)= \left\{\begin{aligned} & \frac{1-\cos \sqrt{x}}{ax},\quad & x>0 \\ & b,\quad & x \le 0 \end{aligned}\right. $ 在 $x=0$ 处连续，则 $(\quad)$
(A) $ab=\frac{1}{2} \quad$ (B) $ab=-\frac{1}{2} \quad$ (c) $ab=0 \quad$ (D) $ab=2 \quad$

　　 2.设函数 $f(x)$ 可导，且 $f(x)f'(x)>0$，则 $(\quad)$
(A) $f(1)>f(-1) \qquad$ (B) $f(1)< f(-1) \quad$
(c) $ \left\lvert f(1) \right\rvert > \left\lvert f(-1) \right\rvert \quad$ (D) $ \left\lvert f(1) \right\rvert < \left\lvert f(-1) \right\rvert $

　　 3.函数 $f(x,y,z)=x^2y+z^2$ 在点 $(1,2,0)$ 处沿向量 $n=(1,2,2)$ 的方向导数为 $(\quad)$
(A) $ 12 \quad$ (B) $ 6 \quad$ (c) $ 4 \quad$ (D) $2 \quad$

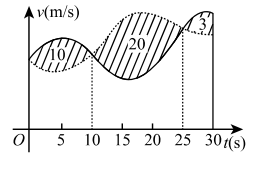
　　 4.甲，乙两人赛跑，计时开始时，甲在乙前方 10（单位：m）处，图中，实线表示甲的速度曲线 $v=v_1(t)$（单位：m/s），虚线表示乙的速度曲线 $v=v_2(t)$，三块阴影部分面积的数值依次是 10，20，3。计时开始后乙追上甲的时刻记为 $t_0$（单位：s），则 $(\quad)$

　　 (A) $t_0=10 \quad$ (B) $15< t_0<20 \quad $ (c) $t_0=25\quad$ (D) $t_0>25$

　　 5.设 $ \boldsymbol{\mathbf{\alpha}} $ 为 $n$ 维单位列向量，$ \boldsymbol{\mathbf{E}} $ 为 $n$ 阶单位矩阵，则 $(\quad)$
(A) $ \boldsymbol{\mathbf{E}} - \boldsymbol{\mathbf{\alpha}} \boldsymbol{\mathbf{\alpha}} ^{\mathrm{T}} $ 不可逆 $\quad$ (B) $ \boldsymbol{\mathbf{E}} + \boldsymbol{\mathbf{\alpha}} \boldsymbol{\mathbf{\alpha}} ^{\mathrm{T}} $ 不可逆
(c) $ \boldsymbol{\mathbf{E}} + 2 \boldsymbol{\mathbf{\alpha}} \boldsymbol{\mathbf{\alpha}} ^{\mathrm{T}} $ 不可逆 $\quad$ (D) $ \boldsymbol{\mathbf{E}} - 2 \boldsymbol{\mathbf{\alpha}} \boldsymbol{\mathbf{\alpha}} ^{\mathrm{T}} $ 不可逆

　　 6.已知矩阵 $ \boldsymbol{\mathbf{A}} = \begin{pmatrix}2&0&0\\0&2&1\\0&0&1\end{pmatrix} , \boldsymbol{\mathbf{B}} = \begin{pmatrix}2&1&0\\0&2&0\\0&0&1\end{pmatrix} , \boldsymbol{\mathbf{C}} = \begin{pmatrix}1&0&0\\0&2&0\\0&0&2\end{pmatrix} $，则 $(\quad)$
(A)$A$ 与 $C$ 相似，$B$ 与 $C$ 相似 $\quad$ (B)$A$ 与 $C$ 相似，$B$ 与 $C$ 不相似
(c)$A$ 与 $C$ 不相似，$B$ 与 $C$ 相似 $\quad$ (D)$A$ 与 $C$ 不相似，$B$ 与 $C$ 不相似 $\quad$

　　 7.设 $A,B$ 为随机事件，若 $0< P(A)<1,0< P(B)<1$，则 $P(A|B)>P(A|\bar{B})$ 的充分必要条件是 $(\quad)$
(A)$P(B|A)>P(B|\bar{A}) \quad$ (B)$P(B|A)< P(B|\bar{A}) \quad$
(c)$P(\bar{B}|A)>P(B|\bar{A}) \quad$ (D)$P(\bar{B}|A)< P(B|\bar{A}) \quad$

　　 8.设 $X_1,X_2,\dots,X_n \quad (n \ge 2)$ 为来自总体 $N(\mu,1)$ 的简单随机样本，记 $\displaystyle \bar{X}=\frac{1}{n} \sum_{i=1}^n X_i$，则下列结论中不正确的是 $(\quad)$
(A)$\displaystyle \sum_{i=1}^n (X_i-\mu)$ 服从 $\chi^2$ 分布 $\quad$ (B)$2(X_n-X_1)^2$ 服从 $\chi^2$ 分布
(c)$\displaystyle \sum_{i=1}^n (X_i-\bar{X})$ 服从 $\chi^2$ 分布 $\quad$ (D)$n(\bar{X}-\mu)^2$ 服从 $\chi^2$ 分布

2. 填空题

　　 1.已知函数 $ \displaystyle f(x)=\frac{1}{1+x^2}$ ，则 $f^{(3)}(0)=(\quad)$。

　　 2.微分方程 $y''+2y'+3y=0$ 的通解为 $y=(\quad)$。

　　 3.若曲线积分 $\displaystyle \int_L \frac{x \,\mathrm{d}{x-ay \,\mathrm{d}{y} } }{x^2+y^2-1}$ 在区域 $D=\{(x,y)|x^2+y^2<1\}$ 内与路径无关，则 $a=(\quad)$。

　　 4.幂级数 $\displaystyle \sum_{n=1}^\infty (-1)^{n-1} nx^{n-1}$ 在区间 $(-1,1) $ 内的和函数 $S(x)=(\quad)$。

　　 5.设矩阵 $ \boldsymbol{\mathbf{A}} = \begin{pmatrix}1&0&1\\1&1&2\\0&1&1\end{pmatrix} $，$ \boldsymbol{\mathbf{\alpha}} _1, \boldsymbol{\mathbf{\alpha}} _2, \boldsymbol{\mathbf{\alpha}} _3$ 为线性无关的 3 维列向量组，则向量组 $ \boldsymbol{\mathbf{A}} \boldsymbol{\mathbf{\alpha}} _1, \boldsymbol{\mathbf{A}} \boldsymbol{\mathbf{\alpha}} _2, \boldsymbol{\mathbf{A}} \boldsymbol{\mathbf{\alpha}} _3$ 的秩为 $(\quad)$。

　　 6.设随机变量 $X$ 的分布函数为 $\displaystyle F(x)=0.5\Phi(x)+0.5\Phi(\frac{x-4}{2})$ ，其中 $\Phi(x)$ 为标准正态分布函数，则 $E(X)=(\quad)$。

3. 解答题

　　 1.设函数 $f(u,v)$ 具有 2 阶连续偏导数，$y=f(e^x,\cos x)$ ,求 $\displaystyle \left.\frac{\mathrm{d} y}{\mathrm{~d} x}\right|_{x=0},\left.\frac{\mathrm{d}^2 y}{\mathrm{~d} x^2}\right|_{x=0}$。

　　 2.求 $\displaystyle \lim_{n \to \infty} \sum_{k=1}^n \frac{k}{n^2} \ln\left(1+\frac{k}{n}\right) $。

　　 3.已知函数 $y(x)$ 由方程 $x^3+y^3-3x+3y-2=0$ 确定，求 $y(x)$ 的极值。

　　 4.设函数 $f(x)$ 在区间 $[0,1]$ 上具有 2 阶导数，且 $\displaystyle f(1)>0,\lim_{x \to 0^+}\frac{f(x)}{x}<0$， 证明：
(1).方程 $f(x)=0$ 在区间 $(0,1)$ 内至少存在一个实根；
(2).方程 $f(x)f''(x)+[f'(x)]^2=0$ 在区间 $(0,1)$ 内至少存在两个不同实根。

　　 5.设薄片型物体 $S$ 是圆锥面 $z=\sqrt{x^2+y^2}$ 被柱面 $z^2=2x$ 割下的有限部分，其上任一点的密度为 $\mu(x,y,z)=9\sqrt{x^2+y^2+z^2}$ 。记圆锥面与柱面的交线为 $C$。
(1).求 $C$ 在 $xOy$ 平面上的投影曲线的方程；
(2).求 $S$ 的质量 $M$。

　　 6.设 3 阶矩阵 $ \boldsymbol{\mathbf{A}} =( \boldsymbol{\mathbf{\alpha}} _1, \boldsymbol{\mathbf{\alpha}} _2, \boldsymbol{\mathbf{\alpha}} _3)$ 有 3 个不同的特征值，且 $ \boldsymbol{\mathbf{\alpha}} _3= \boldsymbol{\mathbf{\alpha}} _1+2 \boldsymbol{\mathbf{\alpha}} _2$。
(1).证明 $r( \boldsymbol{\mathbf{A}} )=2$；
(2).设 $ \boldsymbol{\mathbf{\beta=\alpha_1+\alpha_2+\alpha_3}} $ ，求方程组 $ \boldsymbol{\mathbf{Ax=\beta}} $ 的通解。

　　 7.设二次型 $f(x_1,x_2,x_3)=2x_1^2-x_2^2+ax_3^2+2x_1x_2-8x_1x_3+2x_2x_3$ 在正交变换 $x=Qy$ 下的标准形为 $\lambda_1y_1^2+\lambda_2y_2^2$ ，求 $a$ 的值及一个正交矩阵 $Q$。

　　 8.设随机变量 $X,Y$ 相互独立，且 $X$ 的概率分布为 $\displaystyle P\{X=0\}=P\{X=2\}=\frac{1}{2}$ ，$Y$ 的概率密度为 $f(y)= \left\{\begin{aligned} &2y,\quad & 0< y<1\\&0,\quad &\text{其他} \end{aligned}\right. $。
(1).求 $P\{Y \le E(Y)\}$；
(2).求 $Z=X+Y$ 的概率密度。

　　 9.某工程师为了解一台天平的精度，用该天平对一物体的质量做 $n$ 次测量，该物体的质量 $\mu$ 是已知的。设 $n$ 次测量结果 $X_1,X_2,\dots,X_n$ 相互独立且均服从正态分布 $N(\mu,\sigma^2)$，该工程师记录的是 $n$ 次测量的绝对误差 $Z_i= \left\lvert X_i-\mu \right\rvert \quad (i=1,2,\dots,n)$ 。利用 $Z_1,Z_2,\dots,Z_n$ 估计 $\sigma$。
(1).求 $Z_1$ 的概率密度；
(2).利用一阶矩求 $\sigma$ 的矩估计量；
(3).求 $\sigma$ 的最大似然估计量。