2011 年考研数学试题（数学一）

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 曲线 $y=(x-1)(x-2)^2(x-3)^2(x-4)^2$ 的拐点是 ($\quad$)
   (A) $(1,0)$
   (B) $(2,0)$
   (C) $(3,0)$
   (D) $(4,0)$
2. 设数列 $\{a_n\}$ 单调减少，$\displaystyle \lim_{n\to\infty} a_n=0,S_n=\sum_{k=1}^{n}a_k(n=1,2,\dots)$ 无界，则幂级数 $\displaystyle \sum_{n=1}^\infty a_n(x-1)^n$ 的收敛域为($\quad$)
   (A) $(-1,1]$
   (B) $[-1,1)$
   (C) $[0,2)$
   (D) $(0,2]$
3. 设函数 $f(x)$ 具有二阶连续导数，且 $f(x)>0,f'(0)=0$ ，则函数 $z=f(x)\ln f(y)$ 在点 $(0,0)$ 处取得极小值的一个充分条件是 ($\quad$)
   (A) $f(0)>1,f''(0)>0$
   (B) $f(0)>1,f''(0)<0$
   (C) $f(0)<1,f''(0)>0$
   (D) $f(0)<1,f''(0)<0$
4. 设 $\displaystyle I=\int_{0}^{\frac{\pi}{4}} \ln\left(\sin x\right) \,\mathrm{d}{x} ,J=\int_{0}^{\frac{\pi}{4}} \ln\left(\cot x\right) \,\mathrm{d}{x} ,K=\int_{0}^{\frac{\pi}{4}} \ln\left(\cos x\right) \,\mathrm{d}{x} $，则 $I,J,K$ 的大小关系为 ($\quad$)
   (A) $I< J< K$
   (B) $I< K< J$
   (C) $J< I< K$
   (D) $K< J< I$
5. 设 $ \boldsymbol{\mathbf{A}} $ 为 3 阶矩阵，将 $ \boldsymbol{\mathbf{A}} $ 的第 2 列加到第 1 列得到矩阵 $ \boldsymbol{\mathbf{B}} $，再交换 $ \boldsymbol{\mathbf{B}} $ 的第 2 行与第 3 行得单位矩阵。记 $ \boldsymbol{\mathbf{P}} _1= \begin{pmatrix}1&0&0\\1&1&0\\0&0&1\end{pmatrix} , \boldsymbol{\mathbf{P}} _2= \begin{pmatrix}1&0&0\\0&0&1\\0&1&0\end{pmatrix} $，则 $ \boldsymbol{\mathbf{A}} $=($\quad$)
   (A) $ \boldsymbol{\mathbf{P_1P_2}} $
   (B) $ \boldsymbol{\mathbf{P_1^{-1}P_2}} $
   (C) $ \boldsymbol{\mathbf{P_2P_1}} $
   (D) $ \boldsymbol{\mathbf{P_2P_1^{-1}}} $
6. 设 $ \boldsymbol{\mathbf{A=(\alpha_1,\alpha_2,\alpha_3,\alpha_4)}} $ 是 4 阶矩阵，$A^*$ 为 $A$ 的伴随矩阵。若 $(1,0,1,0) ^{\mathrm{T}} $ 是方程组 $ \boldsymbol{\mathbf{Ax=0}} $ 的一个基础解系，则 $ \boldsymbol{\mathbf{A^*x=0}} $ 的基础解系可为 ($\quad$)
   (A) $ \boldsymbol{\mathbf{\alpha_1,\alpha_3}} $
   (B) $ \boldsymbol{\mathbf{\alpha_1,\alpha_2}} $
   (C) $ \boldsymbol{\mathbf{\alpha_1,\alpha_2,\alpha_3}} $
   (D) $ \boldsymbol{\mathbf{\alpha_2,\alpha_3,\alpha_4}} $
7. 设 $F_1(x)$ 与 $F_2(x)$ 为两个分布函数，其相应的概率密度 $f_1(x)$ 与 $f_2(x)$ 是连续函数，则必为概率密度的是 ($\quad$)
   (A) $f_1(x)f_2(x)$
   (B) $2f_2(x)F_1(x)$
   (C) $f_1(x)F_2(x)$
   (D) $f_1(x)F_2(x)+f_2(x)F_1(x)$
8. 设随机变量 $X$ 与 $Y$ 相互独立，且 $E(X)$ 与 $E(Y)$ 存在，记 $U=\max \{X,Y\},V=\min \{X,Y\}$，则 $E(UV)$=($\quad$)
   (A) $E(U)$· $E(V)$
   (B) $E(X)$· $E(Y)$
   (C) $E(U)$· $E(Y)$
   (D) $E(X)$· $E(V)$
   

1. 填空题

1. 曲线 $\displaystyle y=\int_{0}^{x} \tan t \,\mathrm{d}{t} \quad (0 \le x \le \frac{\pi}{4})$ 的弧长 $s$=($\quad$)
2. 微分方程 $y'+y=e^{-x}\cos x$ 满足条件 $y(0)=0$ 的解为 $y$=($\quad$)
3. 设函数 $\displaystyle F(x,y)=\int_0^{xy} \frac{\sin t}{1+t^2} \,\mathrm{d}{t} $，则 $\displaystyle { \left. \frac{\partial^{2}{F}}{\partial{x}^{2}} \right\rvert _{x=0,y=2}}$=($\quad$)
4. 设 $L$ 是柱面 $x^2+y^2=1$ 与平面 $z=x+y$ 的交线，从 $z$ 轴正向往 $z$ 轴负向看去为逆时针方向，则曲线积分 $\displaystyle \oint_L xz \,\mathrm{d}{x} +x \,\mathrm{d}{y} +\frac{y^2}{2} \,\mathrm{d}{z} $ =($\quad$)
5. 若二次曲面的方程 $x^2+3y^2+z^2+2axy+2xz+2yz=4$ 经正交变换为 $y_1^2+4z_1^2=4$，则 $a$=($\quad$)
6. 设二维随机变量 $(X,Y)$ 服从正态分布 $N(\mu,\mu;\sigma^2,\sigma^2;0)$，则 $E(XY^2)$= ($\quad$)

2. 解答题

1. 求极限 $\displaystyle \lim_{n\to\infty}[\frac{ \ln\left(1+x\right) }{x}]^{\frac{1}{e^x-1}}$.
2. 设函数 $z=f(xy,yg(x))$，其中函数 $f$ 具有二阶连续偏导数，函数 $g(x)$ 可导，且在 $x=1$ 处取得极值 $g(1)=1$。求 $\displaystyle \left. \frac{\partial^2 z}{\partial x \partial y} \right\rvert _{x=1,y=1}$。
3. 求方程 $k\arctan x -x=0$ 不同实根的个数，其中 $ k$ 为参数。
4. (1) 证明：对任意的正整数 $n$，都有 $\frac{1}{n+1}< \ln\left(1+\frac{1}{n}\right) <\frac{1}{n}$ 成立;
   (2)设 $\displaystyle a_n=1+\frac{1}{2}+\dots+\frac{1}{n}-\ln n\quad (n=1,2,\dots )$ ，证明数列 $\{a_n\}$ 收敛。
5. 已知函数 $f(x,y)$ 具有二阶连续偏导数，且 $f(1,y)=0,f(x,1)=0,\iint_D f(x,y) \,\mathrm{d}{x} \,\mathrm{d}{y} =a$ ，其中 $D={(x,y)|0\le x \le 1,0 \le y \le 1}$，计算二重积分 $\displaystyle I=\iint_D xyf''_{xy} \,\mathrm{d}{x} \,\mathrm{d}{y} $
6. 设向量组 $ \boldsymbol{\mathbf{\alpha}} _1=(1,0,1) ^{\mathrm{T}} , \boldsymbol{\mathbf{\alpha}} _2=(0,1,1) ^{\mathrm{T}} , \boldsymbol{\mathbf{\alpha}} _3=(1,3,5) ^{\mathrm{T}} $ 不能由向量组 $ \boldsymbol{\mathbf{\beta}} _1=(1,1,1) ^{\mathrm{T}} , \boldsymbol{\mathbf{\beta}} _2=(1,2,3) ^{\mathrm{T}} , \boldsymbol{\mathbf{\beta}} _3=(3,4,a) ^{\mathrm{T}} $ 线性表示。
   (1)求 $a$ 的值。
   (2)将 $ \boldsymbol{\mathbf{\beta_1,\beta_2,\beta_3}} $ 用 $ \boldsymbol{\mathbf{\alpha_1,\alpha_2,\alpha_3}} $ 线性表示。
7. 设 $ \boldsymbol{\mathbf{A}} $ 为 3 阶实对称矩阵，$ \boldsymbol{\mathbf{A}} $ 的秩为 2，且 $ \boldsymbol{\mathbf{A}} $ $ \begin{pmatrix}1&1\\0&0\\-1&1\end{pmatrix} = \begin{pmatrix}-1&1\\0&0\\1&1\end{pmatrix} $.
   (1)求 $A$ 的所有特征值与特征向量；
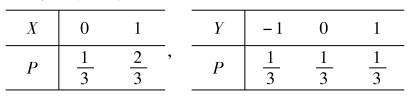
   (2)求矩阵 $ \boldsymbol{\mathbf{A}} $。
8. 设随机变量 $A$ 与 $Y$ 的概率分布分别为
   
   图 1
   且 $P\{X^2=Y^2\}=1$。
   (1)求二维随机变量 $(X,Y)$ 的概率分布；
   (2)求 $Z=XY$ 的概率分布；
   (3)求 $X$ 与 $Y$ 的相关系数 $\rho_{xy}$。
9. 设 $X_1,X_2,\dots,X_n$ 为来自正态总体 $N(\mu_0,\sigma^2)$ 的简单随机样本，其中 $\mu_0$ 已知，$\sigma^2>0$ 未知，$\bar X$ 和 $S^2$ 分别表示样本均值和样本方差。
   (1) 求参数 $\sigma^2$ 的最大似然估计 $ \hat{\sigma} ^2$;
   (2)计算 $E( \hat{\sigma} ^2)$ 和 $D( \hat{\sigma} ^2)$。