北京大学 1999 年 考研 量子力学

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

　　 1. (25 分) 简要回答以下问题
(a) 简述 “不确定原理”（测不准关系），说明其意义。
(b) 试述 “态的叠加原理”，说明其意义。
(c) 全同粒子有什么特性？对波函数有什么要求？举例说明之。

　　 2. (10 分) 已知在 $\hat{J}$ 和 $\hat{L}_z$ 的共同表象中，$\hat{L}_x = \frac{\hbar}{\sqrt{2}} \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}$，试求其本征值和本征函数，并写出在自身表象中的矩阵表示。

　　 3. (15 分) 一个原子在 $z$ 向磁场 $B$ 中，除了能级的塞曼分裂外，还受到 $\Delta \hat{H}_d = \frac{\mu_B^2}{2c^2a_0} B^2 n^2 \sin^2 \theta$ (c.g.s) 的微扰，
(a)] 已知 H 原子基态，$\Psi (1s) = \frac{1}{\sqrt{\pi a_0^3}} e^{-r/a_0}$，求一级微扰能 $ \Delta E_d$。
(b)] 估计这项修正的量级（设 $B=10^4$ 高斯），与塞曼分裂（$\mu_B B$ 量级）比较。
(c)] 分析这个修正的物理意义。

　　 4. (15 分) 氢原子基态 $I^2S_{1/2}$，氢原子核的自旋 $I=1/2$，核自旋与电子相互作用使能级产生超精细分裂。已知超精细相互作用哈密顿量是 $\Delta\hat H = A \vec{I} \cdot \vec{J}$，式中 $\vec{I}, \vec{J}$ 分别是核自旋角动量和电子总角动量，A 是常数
(a) 用 $I J F$ 和表示总角动量 ( $\vec{F} = \vec{I} + \vec{J}$)
(b) 目前 $I = 1/2, J = 1/2$，求基态 $I^2S_{1/2}$ 能级的超精细分裂，并作图表示之。

　　 5. (15 分) 在一维无限深势阱 $V(x) = \begin{cases} 0 & 0 \leq x \leq a \\\\ \infty & x < 0, 0 > a \end{cases}$ 中

　　 (a) 求一个粒子在此势阱中的能量本征值及相应的本征函数。

　　 (b) 一个粒子开始时处于基态，如突然使势阱宽度扩展为 $2a$，问该粒子在扩展后仍处于基态的几率是多少？

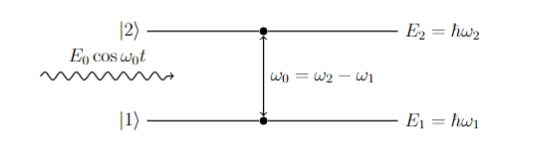
　　 6. (20 分) 一个二能级系统为右图。用圆频率为 $\omega_0$ 的光去照射, 引起受激跃迁。体系的波函数为 $$\Psi = a_1 e^{-i \omega_1 t} |1\rangle + a_2 e^{-i \omega_2 t} |2\rangle,~$$ 相互作用的哈密顿量为 $$\hat{H} = -\vec\mu \cdot \vec{E_0}(e^{i \omega t} + e^{-i \omega t})~$$

　　 (a) 用含时薛定谔方程求 t 时刻粒子处于 $|2\rangle$ 态的几率，证明 $$|a_2(t)|^2 = \sin^2 Vt, \quad V = \frac{\vec\mu_{12} \cdot\vec E_0}{2\hbar},~$$ 初条件为 $t=0$ 时，粒子处于 $|1\rangle$ 态。(注: 忽略 $e^{2i\omega_0 t}$ 项, 又 $\vec\mu_{12} =\vec\mu_{12}$)

　　 (b) 定性分析这个结果的物理意义。