北京大学 2000 年 考研 普通物理

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. (18 分)

　　 1、(8 分)理想气体的比热商(定压热容量与定体热容量之比)记为 $\gamma$，试导出准静态绝热过程的 P-V 方程。

　　 2、(10 分)以理想气体为工作介质，将高温热源温度记为 $T1$，低温热源温度记为 $T2$. 试导出准静态卡诺循环的效率 $\eta$。

2. (16 分)

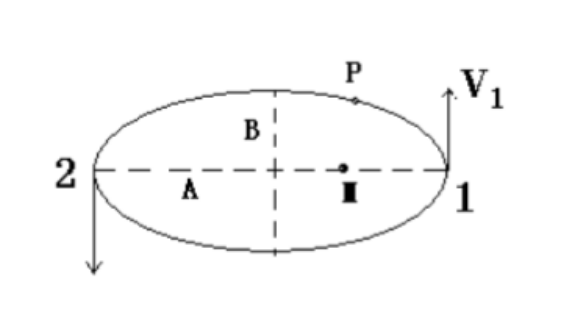
　　 设太阳固定不动，某行星 $P$ 围绕太阳在一椭圆轨道运动，如图所示，其中位置 1 为近太阳点，位置 2 为远太阳点。将太阳的质量记为 $M$，圆半长轴、半短轴分别记为 $A,B$.

　　 利用能量守恒关系和以太阳为参考点的角动量守恒关系，导出 $P$ 在位置 1、2 两处的运动速度大小 $V1,V2$;

　　 已知椭圆面积为 $\pi AB$，导出 $P$ 的轨道运动周期 $T$。

3.（16 分）

　　 半径为 $R$，质量为 $m$ 的匀质乒乓球，可处理为厚度可略的球壳。开始时以角速度 $\omega0$ 围绕它的一条水平直径轴旋转，球心无水平方向速度，今将其轻放在水平地面上，乒乓球与地面之间的滑动摩擦处处相同。

　　 试求乒乓球达到稳定运动状态时，它的转动角速度 $\omega$;

　　 计算从开始到最后达到稳定运动状态的全过程中，乒乓球动能的损失量 $E$'

　　 (已知半径为 $R$，质量为 $m$ 的匀质球壳相对其直径转轴的转动惯量为)

4.（16 分）

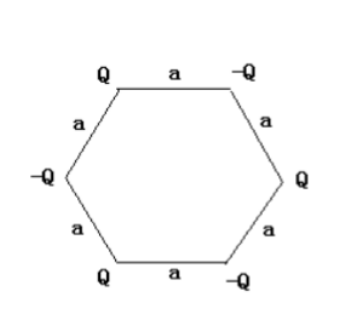
　　 边长为 $a$ 的正六边形分别有固定的点电荷，它们的电量或为 $Q$，或为 $-Q$，分布如图所示

1. 试求因点电荷间相互的静电作用而使系统具有的电势能 $W$:
2. 若用外力将相邻的一对正、负电荷一起(即始终保持其间距不变)缓慢地移到无穷远处，其余固定的点电荷位置保持不变，试求外力作功量 $A$。

5. 16 分）

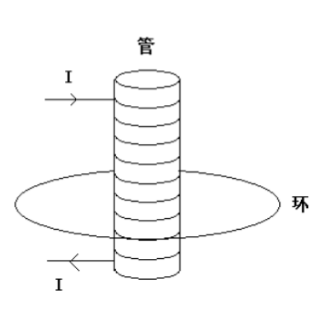
　　 半径为 $r$ 的长直密绕空心螺线管，单位长度的绕线匝数为 $n$，所加交变电流为 $I = I_0 \sin \omega t$ 今在管的垂直平面上放置一个半径为 $2r$,电阻为 $R$ 的导线环，其圆心恰好在螺线管的轴线上。

1. 计算导线环上涡旋电场 $E$ 的值，并在图中画出其正方向;
2. 计算导线环上感应电流 $I_1$;
3. 计算导线环与螺线管之间的互感系数 $M$。

6. (18 分)

　　 用钠黄光($\lambda =5893A$)观察迈克耳孙干涉仪的等倾圆条纹，开始时视场中共看到 10 个亮环，中心为亮斑，然后移动干涉仪一臂的平面镜，先后看到共有 10 个亮环缩进中央，而视场中除中心为亮斑外，还剩下 5 个亮环。试求:

1. 平面镜移动的距离:
2. 开始时中心亮斑的于涉级次;
3. 移动平面镜后最外一个亮环的干涉级次