麦克斯韦妖（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

图
图 1：麦克斯韦妖思想实验的示意图

　　 麦克斯韦妖（Maxwell's demon）是一个思想实验，看似可以推翻热力学第二定律。它由物理学家詹姆斯·克拉克·麦克斯韦于 1867 年提出。\(^\text{[1]}\) 在他最初的信件中，麦克斯韦称这个存在为 “有限的生命” 或 “能够与分子玩一场技巧游戏的存在”。后来开尔文勋爵称其为 “妖”。\(^\text{[2]}\)

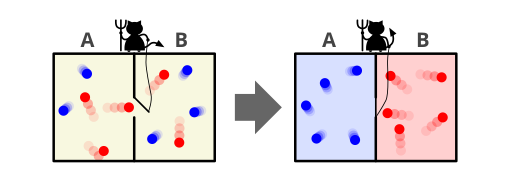
　　 在这个思想实验中，一个妖怪掌管着连接两间气体腔室的门。当单个气体分子（或原子）接近这扇门时，妖怪会迅速开关门：只允许高速运动的分子往一个方向通过，只允许低速运动的分子往另一个方向通过。由于气体的动能温度依赖于其分子的速度，妖怪的操作会使一间腔室升温，另一间腔室降温。这将导致系统的总熵减少，而似乎并未施加任何功，从而违反了热力学第二定律。

　　 麦克斯韦妖的概念在科学哲学和理论物理学中引发了大量争论，直至今日仍在继续。它也推动了人们对热力学与信息论关系的研究。大多数科学家基于理论理由认为，没有任何装置能够以这种方式违反第二定律。也有一些研究者在实验中实现了某种形式的麦克斯韦妖，但它们都在某种程度上与思想实验不同，且没有一个被证明真正违背了热力学第二定律。

1. 这一思想的起源与发展

　　 这个思想实验最早出现在 1867 年 12 月 11 日麦克斯韦写给彼得·格思里·泰特的信中。1871 年，他又在写给约翰·威廉·斯特拉特（John William Strutt，后来的瑞利勋爵）的信里再次提到这一点，随后在 1872 年出版的热力学著作《热论》中正式向公众呈现。\(^\text{[3]}\)

　　 在信件和书籍中，麦克斯韦将那个掌管两腔室之间之门的存在描述为一个 “有限的生命”。由于他是一个虔诚的宗教信徒，他从未使用过 “demon（恶魔）” 一词。相反，威廉·汤姆孙（William Thomson，即开尔文勋爵）才是第一个在 1874 年《自然》期刊中将麦克斯韦的概念称作 “demon” 的人。他暗示自己所指的是希腊神话中的 daemon，即在幕后起作用的超自然存在，而不是一个邪恶的存在。\(^\text{[2][4][5]}\)

2. 原始思想实验

　　 热力学第二定律保证了（通过统计概率），当两个温度不同的物体彼此接触并与宇宙其他部分隔离时，它们最终会演化到一种热力学平衡状态，即二者的温度大致相同。\(^\text{[6]}\) 热力学第二定律也可以表述为：在一个孤立系统中，熵永不减少。\(^\text{[6]}\)

　　 麦克斯韦构思了一个思想实验，以加深对第二定律的理解。他对实验的描述如下：\(^\text{[6][7]}\)

　　 ……假设我们设想一种存在，它的能力如此敏锐，以至于能够追踪到每一个分子的运动轨迹。这样一种存在，其属性和我们一样本质上是有限的，却能够做到我们不可能做到的事情。因为我们已经看到，在一个充满均匀温度空气的容器中，分子的速度并不完全相同，尽管任意选取的大量分子的平均速度几乎完全一致。现在，假设这样的容器被隔板分为两部分，$A$ 和 $B$，隔板上有一个小孔。有一个能够看到单个分子的存在，负责开关这个小孔，使得只有速度较快的分子能够从 $A$ 进入 $B$，而只有速度较慢的分子能够从 $B$ 进入 $A$。这样，他无需做功，就能使 $B$ 的温度升高、$A$ 的温度降低，从而与热力学第二定律相矛盾。

　　 换句话说，麦克斯韦设想了一个被分隔为两部分 $A$ 和 $B$ 的容器。\(^\text{[6][8]}\) 两部分都充满了相同的气体，并且初始温度相同，彼此相邻。一个假想的妖怪观察着两边的分子，并把守着两部分之间的活门。当 $A$ 中一个快于平均速度的分子飞向活门时，妖怪便将其打开，让该分子从 $A$ 飞入 $B$。同样地，当 $B$ 中一个慢于平均速度的分子飞向活门时，妖怪会让它从 $B$ 进入 $A$。结果是，$B$ 部分分子的平均速度提高，而 $A$ 部分的平均速度降低。由于平均分子速度对应于温度，因此 $A$ 的温度下降，$B$ 的温度上升，这与热力学第二定律相悖。此时，若在热源 $A$ 和 $B$ 之间运转一台热机，就能够从这种温差中提取有用功。

　　 值得注意的是，妖怪必须允许分子双向通过，才能仅仅产生温度差；如果它仅允许快于平均速度的分子单向从 $A$ 进入 $B$，那么 $B$ 一侧不仅会升温，还会产生更高的压力。

3. 批评与发展

　　 一些物理学家通过计算指出，如果对包括 “妖怪” 在内的整个系统进行更完整的分析，热力学第二定律实际上并不会被违反。\(^\text{[6][8][9]}\) 物理论证的核心在于：通过计算表明，任何妖怪在分离分子的过程中必然会 “产生” 比其能够消除的更多的熵。换句话说，测定分子速度并选择性地让它们通过 A 与 B 之间的小孔所需的热力学功，要大于由此产生温差所能获得的能量。

　　 对此问题最著名的回应之一是由利奥·西拉尔德在 1929 年提出的，\(^\text{[10]}\) 后来又被莱昂·布里渊进一步发展。\(^\text{[6][8]}\) 西拉尔德指出，现实中的 “麦克斯韦妖” 必然需要某种方式来测量分子的速度，而获取信息的过程本身就需要能量消耗。由于妖怪与气体相互作用，我们必须考虑气体与妖怪的总熵。妖怪在测量过程中所消耗的能量会导致其熵的增加，而这种熵的增加将超过气体熵的减少。

　　 1960 年，罗尔夫·兰道尔对这一论证提出了例外意见。\(^\text{[6][8][11]}\) 他意识到，只要测量过程在热力学上是可逆的，就不一定会增加热力学熵。他提出，这些 “可逆” 的测量可以用来对分子进行分类，从而违反第二定律。然而，由于热力学中的熵与信息论的熵之间存在联系，这也意味着记录下来的测量信息不能被抹除。换句话说，为了判断是否让一个分子通过，妖怪必须获取该分子的状态信息，并要么丢弃它，要么储存它。丢弃信息会立即导致熵增加，而妖怪又不能无限期地存储信息。1982 年，查尔斯·贝内特指出，无论准备得多么充分，妖怪最终都会耗尽存储空间，不得不开始删除先前收集的信息。\(^\text{[8][12]}\) 而删除信息是一个热力学上不可逆的过程，会导致系统熵的增加。尽管贝内特得出的结论与西拉尔德 1929 年论文相同，即 “麦克斯韦妖” 无法违反热力学第二定律，因为必然会产生熵，但他得出结论的原因却不同。关于兰道尔原理，埃里克·卢茨等人在 2012 年通过实验测量了删除信息时的最小能量耗散。卢茨等人还证实，只有当系统的处理速度渐近于零时，才能逼近兰道尔极限。\(^\text{[13]}\) 最近，兰道尔原理也被用来解决统计物理学中一个看似无关的悖论——洛施密特悖论。\(^\text{[14]}\)

　　 约翰·埃尔曼和约翰·D·诺顿则认为，西拉尔德和兰道尔对麦克斯韦妖的解释，是在先验假设 “妖怪不能违反热力学第二定律” 的前提下展开的，并由此推导出妖怪的其他特性，例如在抹除信息时必须消耗能量等。\(^\text{[15][16]}\) 因此，若再用这些推导出的特性来捍卫第二定律，就会陷入循环论证。贝内特后来承认了埃尔曼和诺顿观点的合理性，但同时坚持认为，兰道尔原理解释了真实物理系统为什么不会违反热力学第二定律的机制。\(^\text{[17]}\)

4. 最新进展

　　 尽管兰道尔和贝内特的论证仅仅回答了热力学第二定律与整个西拉尔德发动机（即发动机与妖怪组成的复合系统）循环过程之间的一致性问题，但近年来基于小尺度涨落系统非平衡热力学的方法，为分析每一个子系统中的信息处理过程提供了更深刻的见解。从这种观点看，测量过程可被视为一种相关性（互信息）在发动机与妖怪之间增加的过程，从而使系统熵减少，减少的量正好等于互信息。\(^\text{[18]}\) 如果相关性发生变化，那么诸如热力学第二定律和每个子系统的涨落定理等热力学关系就需要被修正。在外部控制的情况下，可以得到包含互信息的类似第二定律的不等式 \(^\text{[18][19][20]}\)，以及广义的涨落定理。\(^\text{[21]}\) 对于更一般的信息处理过程（包括生物信息处理），既有带互信息的不等式 \(^\text{[22]}\)，也有等式关系成立。\(^\text{[23]}\) 当重复测量被执行时，系统熵的减少由测量序列的熵决定，\(^\text{[18][24][25]}\) 其中考虑到了由于测量间相关性而导致的信息减少。更近一些，卡斯特纳提出，当分子在西拉尔德发动机中被定位于一侧或另一侧时，不确定性原理会迫使系统熵增加，这正是阻止妖怪违反第二定律的原因。\(^\text{[26]}\) 对于原始的妖怪——即通过速度来分类分子的情境，卡斯特纳和施拉特（Schlatter）则认为，不确定性原理会因动量测量导致的分子非局域化，而阻止妖怪完成这种分类。\(^\text{[27]}\)

5. 应用

　　 现实中确实存在 “麦克斯韦妖” 的版本，但所有这些 “真实的妖” 或分子级的妖怪，其降低熵的效应都会被其他地方的熵增加所恰当地抵消。\(^\text{[28]}\) 分子尺度的机制已不再仅限于生物学，它们也是新兴的纳米技术领域的研究对象。粒子物理学家使用的单原子阱，使实验者能够控制单个量子的状态，其方式与麦克斯韦妖类似。

　　 如果假设中的镜像物质确实存在，祖拉布·西拉加泽提出可以设想这样的妖怪：“它们能像第二类永动机一样，从单一热库中提取热能，用于做功，并与普通世界的其余部分隔离开来。然而第二定律并未被违反，因为这些妖怪在世界的隐蔽（镜像）部分通过发射镜像光子而支付了熵的代价。”\(^\text{[29]}\)

6. 实验研究

　　 2007 年，大卫·利宣布制造出一种基于布朗棘轮的纳米装置，这一概念最初由理查德·费曼普及。利的装置能够将化学系统驱离平衡状态，但它必须由外部能源驱动（在此例中为光），因此并未违反热力学原理。\(^\text{[30]}\)

　　 在此之前，包括诺贝尔奖得主弗雷泽·斯托达特在内的研究人员，已经创造出一种名为轮烷的环状分子，它们可以被置于连接两个位置 $A$ 和 $B$ 的轴上。来自任一位置的粒子都会撞击环，使其在两端之间移动。如果在一个系统中放置大量这种装置，那么在任意时刻，一半的装置环位于 $A$ 端，另一半位于 $B$ 端。\(^\text{[31]}\)

　　 利对轴做了一点小改动：当光照射到装置上时，轴的中央会变粗，从而限制环的运动。不过，这种限制只在环位于 $A$ 端时才有效。随着时间推移，环会逐渐被粒子从 $B$ 撞到 $A$，并最终卡在那里，导致系统产生不平衡。在实验中，利能够在几分钟内将数十亿个这样的装置，从最初的 50:50 平衡状态改变为 70:30 的不平衡状态。\(^\text{[32]}\)

　　 2009 年，马克·G·赖岑开发出一种激光原子冷却技术，实现了麦克斯韦当初设想的过程：根据能量将气体中的单个原子分拣到不同的容器中。\(^\text{[6][33][34]}\) 这一新概念是为原子或分子设计的一种 “单向壁”，它允许它们向一个方向移动，却不能返回。单向壁的运作依赖于一个不可逆的原子与分子过程：在特定波长吸收一个光子，然后自发辐射到另一个内部能级。该不可逆过程与由磁场和/或光产生的保守力相耦合。赖岑和其合作者提出使用单向壁来降低原子集合的熵。与此同时，贡萨洛·穆加和安德烈亚斯·鲁施豪普特也独立提出了类似的概念。他们提出的 “原子二极管” 并非用于冷却，而是用来调节原子的流动。赖岑团队在 2008 年的一系列实验中，利用单向壁实现了显著的原子冷却。随后，同年晚些时候，丹尼尔·斯特克及其合作者也演示了原子单向壁的运作。他们的实验基于 2005 年提出的单向壁方案，但未用于冷却。赖岑团队实现的冷却方法被称为 “单光子冷却”，因为平均只需要一个光子就能使原子接近静止。这与其他激光冷却技术形成对比，后者依赖光子的动量并需要两能级的循环跃迁。

　　 2006 年，赖岑、穆加与鲁施豪普特在一篇理论论文中表明，每当一个原子穿过单向壁时，它会散射出一个光子，由此提供了该原子转折点的信息，也就得到了该粒子的能量。来自定向激光的光子被散射到随机方向时所导致的辐射场熵的增加，恰好被原子因被单向壁俘获而减少的熵所抵消。

　　 这种技术常被称作 “麦克斯韦妖”，因为它实现了麦克斯韦所设想的过程：通过将高能和低能原子分拣到不同容器中，从而制造温差。然而，科学家指出，这一过程并没有违反热力学第二定律，\(^\text{[6][35]}\) 也不会导致熵的净减少，\(^\text{[6][35]}\) 更不能用于产生有用的能量。原因在于，该过程所需的激光能量远大于由产生的温差所能获得的能量。原子从激光束中吸收低熵光子，却以随机方向重新发射出来，从而增加了环境的熵。\(^\text{[6][35]}\)

　　 2014 年，佩科拉等人首次在实验中实现了西拉尔德发动机。\(^\text{[36][37]}\) 仅仅一年之后，在早期理论方案 \(^\text{[38]}\) 的基础上，他们又展示了首个 “自主型麦克斯韦妖” 的实验实现。该妖怪能够从系统中提取微观信息，并通过反馈降低其熵。该装置基于两个电容耦合的单电子器件，并集成在同一电子电路上。妖怪的运行可以直接观测到：系统温度下降，而妖怪本身温度上升，这是因为生成互信息所带来的热力学代价。\(^\text{[39]}\)2016 年，佩科拉团队又展示了在耦合单电子电路中的自主妖怪的概念验证，表明可以利用信息作为 “燃料”，为电路中的关键元件降温。\(^\text{[40]}\) 他们还提出，一个由超导电路构成的简单量子比特电路，可能为研究量子版西拉尔德发动机提供基础。\(^\text{[41]}\)

7. 作为隐喻

　　 在计算机科学中，守护进程（daemon，通常是在服务器上运行以响应用户请求的后台进程）的命名源自麦克斯韦妖。\(^\text{[42]}\)

　　 历史学家亨利·布鲁克斯·亚当斯在其手稿《相律在历史中的应用》中，尝试将麦克斯韦妖作为历史的隐喻，尽管他误解并错误应用了这一原理。\(^\text{[43]}\) 亚当斯将历史解释为一个走向 “平衡” 的过程，但他认为好战的国家（在他看来德国是这类国家中最突出的）有逆转这一过程的倾向，即历史中的 “麦克斯韦妖”。亚当斯曾多次试图回应科学同僚对其理论表述的批评，但在 1918 年去世时，该作品仍未完成，最终在他身后才出版。\(^\text{[44]}\)

8. 另见

9. 注释

  1. Cargill Gilston Knott (1911). 《麦克斯韦致泰特的未注明日期信件引文》。载于 Life and Scientific Work of Peter Guthrie Tait。剑桥大学出版社。第 213–215 页。
  2. Thomson, William (1874 年 4 月 9 日). 《能量耗散的动力学理论》。Nature。9 (232): 441–444。Bibcode:1874Natur...9..441T。doi:10.1038/009441c0。
  3. Leff & Rex (2002), 第 370 页。
  4. 《麦克斯韦的分类妖》。Nature。20 (501): 126。1879 年。Bibcode:1879Natur..20Q.126.. doi:10.1038/020126a0。
  5. Weber, Alan S. (2000). Nineteenth Century Science: a Selection of Original Texts。Broadview Press。第 300 页。
  6. Bennett, Charles H. (1987 年 11 月). 《妖怪、发动机与第二定律》。Scientific American。257 (5): 108–116。Bibcode:1987SciAm.257e.108B。doi:10.1038/scientificamerican1187-108。原始 PDF 于 2020 年 12 月 3 日存档。2014 年 11 月 13 日检索。
  7. Maxwell (1871)，重印于 Leff & Rex (1990)，第 4 页。
  8. Sagawa, Takahiro (2012). Thermodynamics of Information Processing in Small Systems。Springer Science and Business Media。第 9–14 页。ISBN 978-4431541677。
  9. Bennett, Charles H.; Schumacher, Benjamin (2011 年 8 月). 《实验室中的麦克斯韦妖》。Nikkei Science: 3–6。2014 年 11 月 13 日检索。
  10. Szilard, Leo (1929). 《智能存在干预下热力学系统熵的减少》。Zeitschrift für Physik。53 (11–12): 840–856Bibcode:1929ZPhy...53..840S。doi:10.1007/bf01341281。S2CID 122038206。引自 Bennett 1987。英文译文可见 NASA 文献 TT F-16723（1976 年出版）。
  11. Landauer, R. (1961). 《计算过程中的不可逆性与热量生成》。IBM Journal of Research and Development。5 (3): 183–191。doi:10.1147/rd.53.0183。2014 年 11 月 13 日检索。重印于 *Vol. 44, No. 1, January 2000, p. 261*。2016-03-03 存档于 Wayback Machine。
  12. Bennett, C. H. (1982). 《计算的热力学——综述》。International Journal of Theoretical Physics (投稿手稿)。21 (12): 905–940。Bibcode:1982IJTP...21..905B。CiteSeerX 10.1.1.655.5610。doi:10.1007/BF02084158。S2CID 17471991。原始 PDF 于 2014-10-14 存档。2017-12-10 检索。
  13. Ball, Philip (2012). 《计算的不可避免代价被揭示》。Nature。doi:10.1038/nature.2012.10186。S2CID 2092541。
  14. Binder, P. M. (2023). 《可逆性悖论：速度反转步骤的作用》。International Journal of Theoretical Physics。62 (9): 200。Bibcode:2023IJTP...62..200B。doi:10.1007/s10773-023-05458-x。
  15. Earman, John & Norton, John D. (1998). 《驱魔人 XIV：麦克斯韦妖之怒。第一部分：从麦克斯韦到西拉尔德》。Studies in History and Philosophy of Modern Physics。29 (4): 435。Bibcode:1998SHPMP..29..435E。doi:10.1016/s1355-2198(98)00023-9。
  16. Earman, John & Norton, John D. (1999). 《驱魔人 XIV：麦克斯韦妖之怒。第二部分：从西拉尔德到兰道尔及其后》。Studies in History and Philosophy of Modern Physics。30 (1): 1。Bibcode:1999SHPMP..30....1E。doi:10.1016/s1355-2198(98)00026-4。
  17. Bennett, Charles H. (2002–2003). 《关于兰道尔原理、可逆计算与麦克斯韦妖的笔记》。Studies in History and Philosophy of Modern Physics。34 (3): 501–510。arXiv:physics/0210005。Bibcode:2003SHPMP..34..501B。doi:10.1016/S1355-2198(03)00039-X。S2CID 9648186。
  18. Cao, F. J.; Feito, M. (2009-04-10). 《反馈控制系统的热力学》。Physical Review E。79 (4): 041118。arXiv:0805.4824。Bibcode:2009PhRvE..79d1118C。doi:10.1103/PhysRevE.79.041118。ISSN 1539-3755。PMID 19518184。
  19. Sagawa, Takahiro; Ueda, Masahito (2008-02-26). 《具有离散量子反馈控制的热力学第二定律》。Physical Review Letters。100 (8): 080403。arXiv:0710.0956。Bibcode:2008PhRvL.100h0403S。doi:10.1103/PhysRevLett.100.080403。PMID 18352605。S2CID 41799543。
  20. Hugo Touchette & Seth Lloyd (2000). 《控制的信信息论极限》。Physical Review Letters。84 (6): 1156–1159。arXiv:chao-dyn/9905039。Bibcode:2000PhRvL..84.1156T。doi:10.1103/PhysRevLett.84.1156。PMID 11017467。S2CID 25507688。
  21. Takahiro Sagawa & Masahito Ueda (2010). 《非平衡反馈控制下的广义 Jarzynski 等式》。Physical Review Letters。104 (9): 090602。arXiv:0907.4914。Bibcode:2010PhRvL.104i0602S。doi:10.1103/PhysRevLett.104.090602。PMID 20366975。S2CID 1549122。
  22. Armen E. Allahverdyan, Dominik Janzing 和 Guenter Mahler (2009). 《信息与热流的热力学效率》。Journal of Statistical Mechanics: Theory and Experiment。2009 (9): P09011。arXiv:0907.3320。Bibcode:2009JSMTE..09..011A。doi:10.1088/1742-5468/2009/09/P09011。S2CID 118440998。
  23. Naoto Shiraishi & Takahiro Sagawa (2015). 《部分掩蔽的非平衡动力学的涨落定理》。Physical Review E。91 (1): 012130。arXiv:1403.4018。Bibcode:2015PhRvE..91a2130S。doi:10.1103/PhysRevE.91.012130。PMID 25679593。S2CID 1805888。
  24. Jarillo, Javier; Tangarife, Tomás; Cao, Francisco J. (2016-01-22). 《离散反馈棘轮在最大功率下的效率》。Physical Review E。93 (1): 012142。Bibcode:2016PhRvE..93a2142J。doi:10.1103/PhysRevE.93.012142。PMID 26871058。
  25. Ruiz-Pino, Natalia; Villarrubia-Moreno, Daniel; Prados, Antonio; Cao-García, Francisco J. (2023-09-12). 《反馈棘轮中的信息》。Physical Review E*。108 (3): 034112。arXiv:2303.16804。Bibcode:2023PhRvE.108c4112R。doi:10.1103/PhysRevE.108.034112。hdl:11441/161971。PMID 37849167。
  26. Kastner, R. E. (2025-03-23). 《麦克斯韦妖被击败：测量的熵代价，而非抹除》。arXiv:2503.18186。2025-03-25 检索。
  27. Kastner, Ruth E.; Schlatter, Andreas (2024-01-08). 《物理不可逆过程中的 “抹除” 熵代价》。Mathematics。12 (2): 206。arXiv:2307.02643。doi:10.3390/math12020206。ISSN 2227-7390。
  28. Loewenstein, Werner R. (2013-01-29). 《心灵中的物理学：大脑的量子视角》。纽约：Basic Books。ISBN 9780465029846。OCLC 778420640。
  29. Silagadze, Z. K. (2007). 《透过镜子的麦克斯韦妖》。Acta Physica Polonica B。38 (1): 101–126。arXiv:physics/0608114。Bibcode:2007AcPPB..38..101S。
  30. Serreli, V; Lee, C. F.; Kay, E. R.; Leigh, D. A. (2007 年 2 月). 《一种分子信息棘轮》。Nature。445 (7127): 523–527。Bibcode:2007Natur.445..523S。doi:10.1038/nature05452。PMID 17268466。S2CID 4314051。
  31. Raizen, Mark G. (2009 年 6 月 12 日). 《原子运动的全面控制》。Science。324 (5933): 1403–1406。Bibcode:2009Sci...324.1403R。doi:10.1126/science.1171506。PMID 19520950。S2CID 10235622。
  32. Raizen, Mark G. (2011 年 3 月). 《妖怪、熵与绝对零度的追寻》。Scientific American。304 (3): 54–59。Bibcode:2011SciAm.304c..54R。doi:10.1038/scientificamerican0311-54。PMID 21438491。2014 年 11 月 14 日检索。
  33. Orzel, Chad (2010 年 1 月 25 日). 《单光子冷却：制造麦克斯韦妖》。Uncertain Principles。ScienceBlogs 网站。2014 年 11 月 14 日检索。
  34. Koski, J. V.; Maisi, V. F.; Sagava, T.; Pekola, J. P. (2014 年 7 月 14 日). 《麦克斯韦妖非平衡动力学中互信息作用的实验观测》。Physical Review Letters。113 (3): 030601。arXiv:1405.1272。Bibcode:2014PhRvL.113c0601K。doi:10.1103/PhysRevLett.113.030601。PMID 25083623。S2CID 119311588。
  35. Koski, J. V.; Maisi, V. F.; Pekola, J. P.; Averin, D. V. (2014 年 9 月 23 日). 《单电子西拉尔德发动机的实验实现》。Proceedings of the National Academy of Sciences of the United States of America*。111 (38): 13786–9。arXiv:1402.5907。Bibcode:2014PNAS..11113786K。doi:10.1073/pnas.1406966111。PMC 4183300。PMID 25201966。
  36. Strasberg, P.; Schaller, G.; Brandes, T.; Esposito, M. (2013 年 1 月 24 日). 《实现麦克斯韦妖的物理模型的热力学》。Physical Review Letters (投稿手稿)。110 (4): 040601。arXiv:1210.5661。Bibcode:2013PhRvL.110d0601S。doi:10.1103/PhysRevLett.110.040601。PMID 25166147。S2CID 5782312。
  37. Koski, J. V.; Kutvonen, A.; Khaymovich, I. M.; Ala-Nissila, T.; Pekola, J. P. (2015). 《片上麦克斯韦妖：一种由信息驱动的制冷机》。Physical Review Letters。115 (26): 260602。arXiv:1507.00530。Bibcode:2015PhRvL.115z0602K。doi:10.1103/PhysRevLett.115.260602。PMID 26764980。S2CID 3393380。
  38. Koski, J. V.; Pekola, J. P. (2016 年 12 月 16 日). 《在电子电路中实现的麦克斯韦妖》。Comptes Rendus Physique。17 (10): 1130–1138。Bibcode:2016CRPhy..17.1130K。doi:10.1016/j.crhy.2016.08.011。
  39. Pekola, J. P.; Golubev, D. S.; Averin, D. V. (2016 年 1 月 5 日). 《基于单量子比特的麦克斯韦妖》。Physical Review B。93 (2): 024501。arXiv:1508.03803。Bibcode:2016PhRvB..93b4501P。doi:10.1103/PhysRevB.93.024501。S2CID 55523206。
  40. Fernando J. Corbató (2002-01-23). 《相信我们的话》。2006-08-20 检索。
  41. Cater (1947), 第 640–647 页；另见 Daub (1970)，重印于 Leff & Rex (1990)，第 37–51 页。
  42. Adams (1919), 第 267 页。

10. 参考文献

11. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利