巨正则系综（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在统计力学中，巨正则系综（grand canonical ensemble，亦称宏观正则系综）是一种用于描述与热库处于热力学平衡（热平衡与化学平衡）的粒子力学系统可能状态的统计系综 \(^\text{[1]}\)。该系综中的系统具有开放性特征——系统可与热库交换能量和粒子，因此系统的不同微观态可能具有不同的总能量与总粒子数。系统的体积、形状及其他外部坐标在所有可能微观态中保持恒定。

　　 巨正则系综的热力学变量为化学势（符号：\(\mu\)）与绝对温度（符号：\(T\)）。该系综的特性还受体积（符号：\(V\)）等力学变量的影响，这些变量决定了系统内部状态的性质。因此，该系综常被称为 \(\mu VT\) 系综，因为这三个物理量均为该系综的固定参数。

1. 基础概念

　　 在统计力学中，巨正则系综的基础概念可表述如下：该系综对每个微观态赋予的概率 \(P\) 由以下指数形式给出： \[ P = e^{(\Omega + \mu N - E)/(kT)},~ \] 式中，\(N\) 表示微观态中的粒子数，\(E\) 为微观态的总能量，\(k\) 为玻尔兹曼常数。

　　 物理量Ω称为巨势，对特定系综而言为常数。当选择不同的 \(\mu,V,T\) 参数时，概率分布和 \(\Omega\) 值将发生改变。巨势Ω具有双重作用：其一作为概率分布的归一化因子（所有微观态的概率之和必须为 1）；其二可通过函数 \(\Omega(\mu,V,T)\) 直接计算许多重要的系综平均值。

　　 当系统允许多种粒子数变化时，概率表达式推广为： \[ P = e^{(\Omega + \mu_1N_1 + \mu_2N_2 + \ldots + \mu_sN_s - E)/(kT)},~ \] 其中，\(\mu_1\) 表示第一种粒子的化学势，\(N_1\) 为对应微观态中该种粒子数，依此类推（\(s\) 为不同粒子种类总数）。需注意粒子数的精确定义（参见下文关于粒子数守恒的注释）。

　　 部分学者将巨正则系综的分布称为广义玻尔兹曼分布 \(^\text{[2]}\)。

　　 巨正则系综特别适用于描述以下系统：系统的几何形状固定，但因与热库接触（例如导体中的电子对应电接地，空腔中的光子对应吸光表面），其能量和粒子数可发生显著涨落。该系综为严格推导无相互作用量子粒子系统的费米-狄拉克统计或玻色-爱因斯坦统计提供了自然框架（参见下文示例）。

　　 公式注记

　　 该概念的另一表述形式将概率写为：\(P = \frac{1}{\mathcal{Z}} e^{(\mu N - E)/(kT)},\) 其中通过巨配分函数 \(\mathcal{Z} = e^{-\Omega/(kT)}\) 替代了巨势Ω。本文中以巨势为基础的公式，均可通过简单的数学变换，利用巨配分函数重新表述。

2. 适用性

　　 巨正则系综是描述与一个热库保持热平衡和化学平衡的孤立系统可能状态的系综（推导过程类似于热浴推导正常正则系综的方法，可以在 Reif\(^\text{[3]}\) 中找到）。巨正则系综适用于任何巨小的系统，无论是小型还是巨型；只需要假设与其接触的热库要巨得多（即取宏观极限）。

　　 系统被孤立的条件是必要的，以确保其具有明确的热力学量和演化。\(^\text{[1]}\) 然而，在实际应用中，通常希望使用巨正则系综来描述与热库直接接触的系统，因为正是这种接触保证了系统的平衡。在这些情况下，使用巨正则系综通常是通过以下方式之一来合理化的：1）假设接触是微弱的，或者 2）将一部分热库的连接纳入到分析中的系统中，以便正确地模拟连接对感兴趣区域的影响。另一种方法是使用理论方法来建模连接的影响，从而得到一个开放的统计系综。

　　 另一个出现巨正则系综的情况是考虑一个巨型的热力学系统（即 “与自身处于平衡状态的系统”）。即使系统的精确条件实际上不允许能量或粒子数的变化，巨正则系综仍然可以用来简化某些热力学性质的计算。原因在于，一旦系统非常巨，各种热力学系综（微正则系综、正则系综）在某些方面会变得与巨正则系综等效。\(^\text{[注 1]}\) 当然，对于小系统，即使在均值上，不同的系综也不再是等效的。因此，当应用于粒子数固定的小系统（如原子核）时，巨正则系综可能会非常不准确。\(^\text{[4]}\)

3. 性质

• 唯一性：对于给定温度和化学势的系统，巨正则系综是唯一确定的，并且不依赖于任意选择，如坐标系的选择（经典力学）或基底的选择（量子力学）。\(^\text{[1]}\) 巨正则系综是唯一一个在常温、常体积和常化学势下重现基本热力学关系的系综。\(^\text{[5]}\)
• 统计平衡（稳态）：尽管底层系统在不断运动，巨正则系综本身并不会随时间演化。实际上，系综仅仅是系统守恒量（能量和粒子数）的函数。\(^\text{[1]}\)
• 与其他系统的热平衡和化学平衡：两个系统，各自由巨正则系综描述，且具有相等的温度和化学势，若接触并达到热平衡和化学平衡[note 2]，它们将保持不变，且最终合并的系统将由同样的温度和化学势的巨正则系综描述。\(^\text{[1]}\)
• 最巨熵：对于给定的机械参数（固定 \(V\)），巨正则系综中对对数概率的平均值 \( -\langle \log P \rangle \)（也称为 “熵”）是对于任何具有相同 \( \langle E \rangle \)、\( \langle N_1 \rangle \) 等的系综（即概率分布 \(P\)）所能达到的最巨值。\(^\text{[1]}\)
• 最小巨势能：对于给定的机械参数（固定 \(V\)）以及给定的 \(T,\mu_1,\cdots,\mu_s\) 的值，巨正则系综的平均值 \({\displaystyle \left\langle E + kT\log P - \mu_{1}N_{1} - \ldots \mu_{s}N_{s} \right\rangle}\) 是任何系综中可能的最小值。\(^\text{[1]}\)

4. 巨势能、系综平均和精确微分

　　 函数 \(\Omega(\mu_1,\dots,\mu_s,V,T)\) 的偏导数给出了重要的巨正则系综平均量：\(^\text{[1][6]}\)

• 粒子数的平均值 \[\langle N_1 \rangle = -\frac{\partial \Omega}{\partial \mu_1}, \quad \dots \quad \langle N_s \rangle = -\frac{\partial \Omega}{\partial \mu_s}~\],
• 平均压强 \[\langle p \rangle = -\frac{\partial \Omega}{\partial V},~\]
• 吉布斯熵 \[S = -k \langle \log P \rangle = -\frac{\partial \Omega}{\partial T},~\]
• 以及平均能量 \[\langle E \rangle = \Omega + \langle N_1 \rangle \mu_1 + \dots + \langle N_s \rangle \mu_s + S T.~\]

　　 精确微分：从上述表达式可以看出，函数 Ω 具有精确的微分 \[ d\Omega = -S dT - \langle N_1 \rangle d\mu_1 - \dots - \langle N_s \rangle d\mu_s - \langle p \rangle dV.~ \] 热力学第一定律：将上述关系式代入 Ω 的精确微分，得到类似热力学第一定律的方程，唯一不同的是某些量带有平均符号：\(^\text{[1]}\) \[ d\langle E \rangle = T dS + \mu_1 d\langle N_1 \rangle + \dots + \mu_s d\langle N_s \rangle - \langle p \rangle dV.~ \] 热力学波动：能量和粒子数的方差为 \(^\text{[7][8]}\) \[ \langle E^2 \rangle - \langle E \rangle^2 = k T^2 \frac{\partial \langle E \rangle}{\partial T} + k T \mu_1 \frac{\partial \langle E \rangle}{\partial \mu_1} + k T \mu_2 \frac{\partial \langle E \rangle}{\partial \mu_2} + \dots ,~ \] \[ \langle N_1^2 \rangle - \langle N_1 \rangle^2 = k T \frac{\partial \langle N_1 \rangle}{\partial \mu_1}.~ \] 波动中的关联：粒子数和能量的协方差为 \(^\text{[1]}\) \[ \langle N_1 N_2 \rangle - \langle N_1 \rangle \langle N_2 \rangle = k T \frac{\partial \langle N_2 \rangle}{\partial \mu_1} = k T \frac{\partial \langle N_1 \rangle}{\partial \mu_2}.~ \] \[ \langle N_1 E \rangle - \langle N_1 \rangle \langle E \rangle = k T \frac{\partial \langle E \rangle}{\partial \mu_1}.~ \]

5. 例子系综

　　 巨正则系综的有用性在下面的例子中得到了说明。在每个例子中，巨正则势能是基于以下关系计算的： \[ \Omega = -kT \ln \left( \sum_{\text{microstates}} e^{(\mu N - E)/(kT)}\right)~ \] 这个关系是为了使微观状态的概率总和为 1 所必需的。

非相互作用粒子的统计

　　 玻色子和费米子（量子）

　　 在量子系统中，如果有许多非相互作用的粒子，则热力学计算是简单的。\(^\text{[9]}\) 由于粒子是非相互作用的，可以计算一系列单粒子驻留态，每个驻留态代表一个可以被包含进系统总量子态的可分离部分。为了避免将这些 “状态” 与总的多体态混淆，我们暂时称这些单粒子驻留态为轨道，并规定每个可能的粒子内部属性（如自旋或极化）都算作一个单独的轨道。每个轨道可以被粒子（或多个粒子）占据，或者保持为空。

　　 由于粒子是非相互作用的，我们可以从以下角度来看待：每个轨道形成一个独立的热力学系统。因此，每个轨道都是一个独立的巨正则系综，它如此简单，以至于其统计可以立即在此推导出来。我们聚焦于仅一个标记为 \(i\) 的轨道，对于该轨道中 \(N_i\) 个粒子的一个微观状态，其总能量为 \(N_i\epsilon_i\)，其中 \(\epsilon_i\) 是该轨道的特征能级。该轨道的巨正则势能由以下两种形式之一给出，具体取决于该轨道是玻色子轨道还是费米子轨道：

• 对于费米子，泡利排斥原理只允许轨道有两个微观状态（占据 0 或 1），因此得到一个二项级数： \[ \Omega_i = -kT \ln \left( \sum_{N_i=0}^{1} e^{(N_i \mu - N_i \epsilon_i)/kT} \right) = -kT \ln \left( 1 + e^{(\mu - \epsilon_i)/kT} \right)~ \]
• 对于玻色子，\(N_i\) 可以是任何非负整数，并且由于粒子不可区分，每个 \(N_i\) 的值都算作一个微观状态，从而得到一个几何级数： \[ \Omega_i = -kT \ln \left( \sum_{N_i=0}^{\infty} e^{(N_i \mu - N_i \epsilon_i)/kT} \right) = +kT \ln \left( 1 - e^{(\mu - \epsilon_i)/kT} \right)~ \]

　　 在每种情况下，值 \(\langle N_i \rangle = -\frac{\partial \Omega_i}{\partial \mu}\) 给出了轨道上粒子的热力学平均数：费米-狄拉克分布适用于费米子，玻色-爱因斯坦分布适用于玻色子。再次考虑整个系统，通过将所有轨道的 \(\Omega_i\) 相加，得到总的巨正则势能。

　　 不可区分的经典粒子

　　 在经典力学中，同样可以考虑不可区分的粒子（事实上，不可区分性是以一致的方式定义化学势的前提条件；所有给定种类的粒子必须是可以互换的 \(^\text{[1]}\)）。我们可以将具有巨致均匀能量 \(\epsilon_i\) 的单粒子相空间区域视为一个标记为 \(i\) 的 “轨道”。

　　 由于这个轨道实际上包含许多（无限多个）不同的状态，因此会出现两个复杂问题。简要来说：

• 由于多粒子相空间中包含了 \(N_i!\) 个相同的实际状态副本（由粒子的不同精确状态排列组合形成），因此需要一个 \(1/N_i!\) 的重计数修正。
• 轨道的宽度是任意选择的，因此还需要一个与 \(N_i\) 无关的比例因子。

　　 由于 \(1/N_i!\) 的重计数修正，求和现在呈现出指数级幂级数的形式， \[ \Omega_i \propto -kT \ln \left( \sum_{N_i=0}^{\infty} \frac{1}{N_i!} e^{(N_i \mu - N_i \epsilon_i)/(kT)} \right) \propto -kT \ln \left( e^{e^{(\mu - \epsilon_i)/(kT)}} \right) \propto -kT e^{\frac{\mu - \epsilon_i}{kT}},~ \] 值 \(\langle N_i \rangle \propto -\frac{\partial \Omega_i}{\partial \mu}\) 对应于麦克斯韦-玻尔兹曼统计。

孤立原子的电离

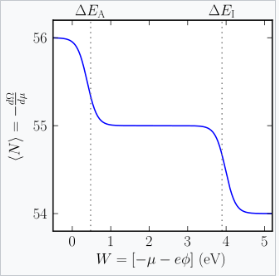
　　 巨正则系综可以用来预测一个原子更倾向于处于中性状态还是电离状态。一个原子能够存在于与中性状态相比，电子数更多或更少的电离状态。如下面所示，电离状态可能在热力学上更为优选，具体取决于环境。考虑一个简化模型，其中原子可以处于中性状态或两个电离状态之一（详细计算还包括激发态和状态的简并因子 \(^\text{[10][11]}\)）：

• 带电中性态，具有 \( N_0 \) 个电子和能量 \( E_0 \)。
• 氧化态（\( N_0 - 1 \) 个电子），能量为 \( E_0 + \Delta E_I + q\phi \)；
• 还原态（\( N_0 + 1 \) 个电子），能量为 \( E_0 - \Delta E_A - q\phi \)。

　　 其中，\( \Delta E_I \) 和 \( \Delta E_A \) 分别是原子的电离能和电子亲和能；\( \phi \) 是原子附近真空中的局部静电势，\( -q \) 是电子的电荷。

　　 其中 \( \Delta E_I \) 和 \( \Delta E_A \) 分别是原子的电离能和电子亲和能；\(\phi\) 是原子附近真空中的局部静电势，\( -q \) 是电子的电荷。

　　 在这种情况下，巨势能由下式确定： \[ \Omega = -kT \ln \left( e^{(\mu N_0 - E_0)/(kT)} + e^{(\mu N_0 - \mu - E_0 - \Delta E_I - q\phi)/(kT)} + e^{(\mu N_0 + \mu - E_0 + \Delta E_A + q\phi)/(kT)} \right)~ \] \[ = E_0 - \mu N_0 - kT \ln \left( 1 + e^{(-\mu - \Delta E_I - q\phi)/(kT)} + e^{(\mu + \Delta E_A + q\phi)/(kT)} \right)~ \] 其中，\( -q\phi - \mu \) 在此情况下至关重要，它决定了不同状态之间的平衡。这个值由原子周围的环境决定。

• 如果将一个孤立原子放置在金属箱中，则 \( -q\phi - \mu = W \)，为箱体衬里材料的功函数。如果 \( W > \Delta E_I \)，则原子更倾向于作为正离子存在。这个自发的表面电离效应已被用作铯离子源。\(^\text{[12]}\)
• 如果原子周围有一个理想的电子气，其电子密度为 \( n_e \)，则有：\(\exp \left((\mu + q\phi)/kT\right) = n_e \lambda_{\text{th}}^{3}/2\) 代入这一公式后得到萨哈电离方程。\(^\text{[10]}\)
• 在半导体中，掺杂原子的电离可以很好地用这个集合描述。[11]在半导体中，导带边缘 \( \epsilon_C \) 充当真空能级的角色（取代 \( -q\phi\)），而 \( \mu \) 被称为费米能级。当然，掺杂原子的电离能和电子亲和能与它们在真空中的值相比有很巨改变。典型的硅中供体掺杂物磷，其电离能 \( \Delta E_I = 45 \, \text{meV} \)。\(^\text{[13]}\)

6. 化学势的含义，广义的‘粒子数’

　　 为了使粒子数具有相关联的化学势，它必须在系统的内部动力学过程中保持守恒，只有在系统与外部储备交换粒子时，粒子数才能改变。

　　 如果粒子可以在系统的动力学过程中由能量创造出来，那么与之相关的 \( \mu N \) 项就不应该出现在巨正则系综的概率表达式中。实际上，这与要求该类粒子的化学势 \( \mu = 0 \) 是一样的。黑腔中的光子就是这种情况，它们的数量由于腔壁上的吸收和辐射而不断变化。（另一方面，在高度反射的腔中，光子可以被守恒，并且具有非零的 \( \mu \)。\(^\text{[14]}\)

　　 在某些情况下，粒子数并不是守恒的，\( N \) 代表的是一个更抽象的守恒量：

• 化学反应：化学反应可以将一种分子转化为另一种分子；如果发生反应，则必须定义 \( N_i \) 使得它们在化学反应过程中保持不变。
• 高能粒子物理学：普通粒子可以从纯能量中生成，前提是同时生成相应的反粒子。如果允许这种过程，那么粒子和反粒子的数量都不再守恒。相反，\( N = (\text{粒子数} - \text{反粒子数}) \) 是守恒的。\(^\text{[15][注释 3]}\) 随着粒子能量的增加，粒子类型之间的转化可能性增多，因此真正守恒的粒子数越来越少。在最高的能量下，唯一守恒的量是电荷、弱同位旋和重子–轻子数差。

　　 另一方面，在某些情况下，单一类型的粒子可能具有多个守恒量：

• 封闭舱室：在由多个舱室组成的系统中，这些舱室共享能量但不共享粒子，可以为每个舱室单独设置化学势。例如，电容器由两个相互隔离的导体组成，并通过施加电子化学势差来充电。
• 慢速平衡：在一些准平衡状态下，同一位置可能存在两种不同的相同类型的粒子群体，它们各自内部达到平衡，但彼此之间不平衡。虽然严格来说不是平衡态，但命名准平衡化学势是有用的，这些化学势在不同的粒子群体之间可能是不同的。例子：（半导体物理学）导带和价带中存在不同的准费米能级（电子化学势）；（自旋电子学）自旋向上和自旋向下的化学势不同；（低温学）正氢和反氢的化学势不同。

7. 统计系综的精确表达式

　　 统计系综的精确数学表达式根据所考虑的力学类型（量子力学或经典力学）具有不同的形式，因为 “微观状态” 的概念有很巨区别。在量子力学中，巨正则系综提供了一个简单的描述，因为对角化提供了系统的不同微观状态，每个状态具有明确的能量和粒子数。经典力学的情况更为复杂，因为它涉及的不是静止状态，而是对经典相空间的积分。

量子力学

　　 关于量子力学中系综表示的更多信息：统计系综（数学物理） 量子力学中的统计系综通过密度矩阵表示，记作 \( \hat{\rho} \)。巨正则系综就是密度矩阵：

　　 \[ \hat{\rho} = \exp \left( \frac{1}{kT} \left( \Omega + \mu_1 \hat{N}_1 + \dots + \mu_s \hat{N}_s - \hat{H} \right) \right)~ \]

　　 其中，\( \hat{H} \) 是系统的总能量算符（哈密顿量），\( \hat{N}_1 \) 是系统中类型 1 粒子的总粒子数算符，\( \hat{N}_2 \) 是类型 2 粒子的总粒子数算符，以此类推。\( \exp \) 是矩阵指数算符。巨势能 \( \Omega \) 由概率归一化条件确定，即密度矩阵的迹为 1：\(\text{Tr} \hat{\rho} = 1\) \[ e^{-\frac{\Omega}{kT}} = \text{Tr} \exp \left( \frac{1}{kT} \left( \mu_1 \hat{N}_1 + \dots + \mu_s \hat{N}_s - \hat{H} \right) \right)~ \] 请注意，对于巨正则系综，算符 \( \hat{H} \)、\( \hat{N}_1 \) 等的基态都是具有多个粒子的福克空间中的状态，且密度矩阵在相同的基上定义。由于能量和粒子数都是分别守恒的，这些算符是彼此对易的。

　　 巨正则系综可以用简单的形式通过 bra–ket 表示法来写出，因为在能量和粒子数算符是彼此对易的情况下，可以找到一组同时的本征态 \( |\psi_i \rangle \)，其中 \( \hat{H}|\psi_i \rangle = E_i |\psi_i \rangle \)，\( \hat{N}_1 |\psi_i \rangle = N_{1,i} |\psi_i \rangle \)，依此类推。给定这样的本征基，巨正则系综可以简单地写为： \[ \hat{\rho} = \sum_i e^{\frac{\Omega + \mu_1 N_{1,i} + \dots + \mu_s N_{s,i} - E_i}{kT}} |\psi_i \rangle \langle \psi_i |~ \] \[ e^{-\frac{\Omega}{kT}} = \sum_i e^{\frac{\mu_1 N_{1,i} + \dots + \mu_s N_{s,i} - E_i}{kT}}~ \] 其中，求和是对所有状态的完整集合进行的，状态 \( i \) 的总能量为 \( E_i \)，类型 1 的粒子数为 \( N_{1,i} \)，类型 2 的粒子数为 \( N_{2,i} \)，依此类推。

经典力学

　　 关于经典力学中系综表示的更多信息：统计系综（数学物理） 在经典力学中，大正则系综通过定义在多个不同维度的相空间上的联合概率密度函数表示，记作 \( \rho(N_1, \dots, N_s, p_1, \dots, p_n, q_1, \dots, q_n) \)，其中 \( p_1, \dots, p_n \) 和 \( q_1, \dots, q_n \) 是系统内部自由度的规范坐标（广义动量和广义坐标）。大正则系综的表达式比大正则系综更为精细，因为：

• 粒子数及因此坐标数 \( n \) 在不同的相空间之间变化；
• 关键是要考虑是否将相似的粒子置换视为不同的状态。

　　 在一个粒子系统中，自由度的数量 \( n \) 取决于粒子数，并且这种依赖关系取决于具体的物理情况。例如，在三维的单原子气体中，\( n = 3N \)，然而在分子气体中，还会有转动和振动自由度。

　　 大正则系综的概率密度函数为： \[ \rho = \frac{1}{h^n C} e^{\frac{\Omega + \mu_1 N_1 + \dots + \mu_s N_s - E}{kT}}~ \] 其中：

• \( E \) 是系统的能量，是相空间（\( N_1, \dots, N_s, p_1, \dots, p_n, q_1, \dots, q_n \)）的函数；
• \( h \) 是一个任意但预定的常数，单位为能量×时间，用来设定一个微观状态的范围，并为 \( \rho \) 提供正确的维度。\(^\text{[注 4]}\)
• \( C \) 是一个过度计数修正因子（见下文），是 \( N_1, \dots, N_s \) 的函数。

　　 同样，\( \Omega \) 的值通过要求 \( \rho \) 是一个归一化的概率密度函数来确定： \[ e^{-\frac{\Omega}{kT}} = \sum_{N_1=0}^{\infty} \dots \sum_{N_s=0}^{\infty} \int \dots \int \frac{1}{h^n C} e^{\frac{\mu_1 N_1 + \dots + \mu_s N_s - E}{kT}} dp_1 \dots dq_n~ \] 这个积分是在给定粒子数的相空间上进行的。

　　 过度计数修正

　　 在流体（气体、液体、等离子体）的统计力学中，一个著名的问题是如何处理相似或相同性质的粒子：它们应被视为可区分的还是不可区分的？在系统的运动方程中，每个粒子始终被视为一个可区分的实体，但系统中也存在有效的状态，其中每个粒子的位置仅仅被交换：这些状态在相空间中代表着不同的位置，但似乎是等价的。

　　 如果相似粒子的置换被视为计数为不同的状态，那么上面的因子 \( C \) 就是简单的 \( C = 1 \)。从这个角度来看，系综将每一个置换状态视为一个独立的微观状态。虽然最初看起来无害，但这会导致一个在经典系综中严重非广延的熵问题，今天称为吉布斯悖论。在大正则系综中，进一步的逻辑不一致发生了：可区分的置换数量不仅依赖于系统中有多少粒子，还依赖于储存库中有多少粒子（因为系统可能与储存库交换粒子）。在这种情况下，熵和化学势是非广延的，但也定义不清，依赖于一个应该是无关紧要的参数（储存库大小）。

　　 为了解决这些问题，必须认为两个相似粒子的交换（无论是在系统内，还是在系统与储存库之间）不会给系统带来一个不同的状态。\(^\text{[1][注 5]}\) 为了将这一事实纳入考虑，积分仍然在完整的相空间上进行，但结果会除以 \[ C = N_1! N_2! \dots N_s!~ \] 这是可能的不同置换的数量。除以 \( C \) 使得在对所有相空间进行积分时，过度计数得到了巧妙的修正。

　　 当然，可以在大正则系综中包含可区分的粒子类型——每种可区分的类型 \( i \) 都由一个单独的粒子计数器 \( N_i \) 和化学势 \( \mu_i \) 追踪。因此，将 “完全可区分” 的粒子包含在大正则系综中的唯一一致方式是考虑每一种可能的可区分粒子类型，并为每种类型追踪一个单独的粒子计数器和单独的化学势。

8. 另见

• 微正则系综
• 经典系综

9. 注释

1. 引用 Reif 的话：“为了计算物理量的平均值，宏观系统是孤立的，还是与一个只能交换能量的储存库接触，或与一个可以交换能量和粒子的储存库接触，这并没有明显的区别。[…] 在一些问题中，固定粒子数的约束比较麻烦，因此可以通过将实际情况近似为大正则分布来轻松绕过这个复杂性。”
2. 热接触和化学接触意味着系统能够通过连接交换能量和粒子。该连接必须足够弱，以免显著扰动系统的微观状态。
3. 当然，非常高的温度是粒子-反粒子对的显著热生成所必需的，例如，为了电子-正电子对的产生，温度需要达到大约 \(10^9\) K，因此这一过程对于日常热力学并不构成问题。
4. （历史注）吉布斯最初的系综实际上设定了 \( h = 1 \)[能量单位] × [时间单位]，导致某些热力学量（如熵和化学势）的单位依赖性。自从量子力学的出现以来，\( h \) 通常被取为普朗克常数，以便获得与量子力学的半经典对应。
5. 这可以与经典系综进行比较，在经典系综中，将粒子视为可区分是可选的；这只会在熵中引入与 \( N \) 相关的误差，只要 \( N \) 保持不变，这个误差是不可观测的。然而，通常情况下，没有这样的自由度：“当系统中的粒子数被视为变量时，定义的相位的平均概率指数对应于熵。”（吉布斯）

10. 参考文献

1. Gibbs, Josiah Willard (1902). 《统计力学的基本原理》。纽约：查尔斯·斯克里布纳之子出版社。
2. Gao, Xiang; Gallicchio, Emilio; Roitberg, Adrian (2019). "广义玻尔兹曼分布是唯一使吉布斯-香农熵等于热力学熵的分布"。《化学物理学杂志》。151 (3): 034113. arXiv:1903.02121. Bibcode:2019JChPh.151c4113G. doi:10.1063/1.5111333. PMID 31325924. S2CID 118981017.
3. Reif, F. (1965). 《统计和热物理基础》。麦格劳-希尔出版社。ISBN 9780070518001.
4. Chaudhuri, G.; Gupta, S. (2007). "经典和大正则版本热力学模型中的比热和双模态性"。《物理评论 C》。76 (1): 014619. arXiv:0704.0288. Bibcode:2007PhRvC..76a4619C. doi:10.1103/PhysRevC.76.014619. S2CID 119152931.
5. Gao, Xiang (2022 年 3 月). "系综理论的数学"。《物理学结果》。34: 105230. arXiv:2006.00485. Bibcode:2022ResPh..3405230G. doi:10.1016/j.rinp.2022.105230. S2CID 221978379.
6. "5.1 吉布斯分布"
7. "存档副本" (PDF)。原文已存档于 2013 年 10 月 19 日。于 2013 年 5 月 2 日检索。
8. "讲义 9. NPT 和大正则系综" (PDF)。micro.stanford.edu。2011 年 1 月 26 日。于 2023 年 11 月 4 日检索。
9. Srivastava, R. K.; Ashok, J. (2005). 《统计力学》。新德里：PHI 学习有限公司。ISBN 9788120327825.
10. Ter Haar, D. (1955). "关于在统计力学中使用大正则系综：Saha 公式的新推导"。《美国物理学杂志》。23 (6): 326–331. doi:10.1119/1.1934002.
11. Balkanski, M.; Wallis, R.F. (2000). 《半导体物理学与应用》。牛津大学出版社。ISBN 0198517408.
12. Alton, G. D. (1988). "用多孔钨电离器表征铯表面电离源。我"。《科学仪器评论》。59 (7): 1039–1044. Bibcode:1988RScI...59.1039A. doi:10.1063/1.1139776.
13. "2. 半导体掺杂技术"
14. Ciuti, C. (2014). "光子玻色-爱因斯坦凝聚中的统计闪烁"。《物理学》。7: 7. Bibcode:2014PhyOJ...7....7C. doi:10.1103/Physics.7.7.
15. Burakovsky, L.; Horwitz, L. P.; Schieve, W. C. (1996). "新的相对论性高温玻色-爱因斯坦凝聚"。《物理评论 D》。54 (6): 4029–4038. arXiv:hep-th/9604039. Bibcode:1996PhRvD..54.4029B. doi:10.1103/PhysRevD.54.4029. PMID 10021081. S2CID 18182534.”