刘维尔定理（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在物理学中，李维尔定理（Liouville's theorem）以法国数学家约瑟夫·李维尔（Joseph Liouville）命名，是经典统计力学和哈密顿力学中的一个关键定理。该定理断言，系统的相空间分布函数在系统的轨迹上是恒定的——即在相空间中，围绕给定系统点的系统点的密度随着时间变化保持不变。这种时间不变的密度在统计力学中称为经典的先验概率。[1]

　　 李维尔定理适用于守恒系统，即在没有摩擦效应或摩擦效应可以忽略的系统。对于这种系统的普遍数学表述是保持度量不变的动力系统。当系统具有可以解释为位置和动量的自由度时，李维尔定理适用；并非所有保持度量不变的动力系统都有这些自由度，但哈密顿系统有。在共轭位置和动量坐标的数学框架中，李维尔定理在辛几何的数学设置下得到了描述。李维尔定理忽略了化学反应的可能性，在化学反应中，粒子的总数可能随时间变化，或能量可能转移到内部自由度。李维尔定理有扩展形式，可以涵盖这些广义的情形，包括随机系统。[2]

1. 李维尔方程

　　 李维尔方程描述了相空间分布函数的时间演化。尽管该方程通常被称为 “李维尔方程”，但约西亚·威拉德·吉布斯（Josiah Willard Gibbs）是第一个认识到这个方程作为统计力学基本方程重要性的人。[3][4] 它之所以被称为李维尔方程，是因为其对非正则系统的推导使用了李维尔在 1838 年首次推导出的一个恒等式。[5][6] 考虑一个哈密顿动力学系统，具有正则坐标 \( q_i \) 和共轭动量 \( p_i \)，其中 \( i = 1, \dots , n \)。那么，相空间分布函数 \( \rho(p,q) \) 决定了系统出现在微小相空间体积 \( \mathrm{d}^n q \, \mathrm{d}^n p \) 中的概率 \( \rho(p,q) \, \mathrm{d}^n q \, \mathrm{d}^n p \)。

　　 李维尔方程描述了 \( \rho(p,q;t) \) 在时间 \( t \) 中的演化： \[ \frac{d\rho}{dt} = \frac{\partial \rho}{\partial t} + \sum_{i=1}^{n} \left( \frac{\partial \rho}{\partial q_i} \dot{q}_i + \frac{\partial \rho}{\partial p_i} \dot{p}_i \right) = 0.~ \] 时间导数用点表示，并根据系统的哈密顿方程进行求值。这个方程表明相空间中的密度守恒（这是吉布斯对该定理的称呼）。李维尔定理表明：

　　 分布函数沿着相空间中的任何轨迹保持不变。

　　 李维尔定理的证明使用了 n 维散度定理。该证明基于这样一个事实：分布函数 \(\rho\) 的演化服从一个二维 n 维的连续性方程： \[ \frac{\partial \rho}{\partial t} + \sum_{i=1}^{n} \left( \frac{\partial (\rho \dot{q}_i)}{\partial q_i} + \frac{\partial (\rho \dot{p}_i)}{\partial p_i} \right) = 0~ \] 也就是说，三元组 \((\rho, \rho \dot{q}_i, \rho \dot{p}_i)\) 是一个守恒流。注意到，这个式子和李维尔方程的区别在于以下项： \[ \rho \sum_{i=1}^{n} \left( \frac{\partial \dot{q}_i}{\partial q_i} + \frac{\partial \dot{p}_i}{\partial p_i} \right) = \rho \sum_{i=1}^{n} \left( \frac{\partial^2 H}{\partial q_i \, \partial p_i} - \frac{\partial^2 H}{\partial p_i \, \partial q_i} \right) = 0~ \] 其中，\( H \) 是哈密顿量，并且偏导数 \(\partial \dot{q}_i/\partial q_i\) 和 \(\partial \dot{p}_i/\partial p_i\) 是使用哈密顿运动方程计算的。 也就是说，将相空间中的运动看作系统点的 “流体流动”，密度的对流导数 \(d\rho/dt\) 为零是由连续性方程得出的，因为相空间中的 “速度场” \((\dot{p}, \dot{q})\) 的散度为零（这由哈密顿关系得出）。[7]

2. 其他表述

泊松括号

　　 上面的定理通常可以用泊松括号重新表述为： \[ \frac{\partial \rho}{\partial t} = \{ H, \rho \}~ \] 或者，用线性李维尔算符（或李维尔算子）表示为： \[ i \hat{\mathbf{L}} = \sum_{i=1}^{n} \left[ \frac{\partial H}{\partial p_i} \frac{\partial}{\partial q_i} - \frac{\partial H}{\partial q_i} \frac{\partial}{\partial p_i} \right] = -\{ H, \bullet \}~ \] 因此， \[ \frac{\partial \rho}{\partial t} + i \hat{\mathbf{L}} \rho = 0~ \]

遍历理论

　　 在遍历理论和动力学系统中，基于前述的物理考虑，有一个相应的结果也被称为李维尔定理。在哈密顿力学中，相空间是一个光滑的流形，天然地配备有一个光滑的度量（在局部范围内，这个度量是 6n 维的 Lebesgue 度量）。该定理指出，这个光滑度量在哈密顿流动下是不变的。更一般地，可以描述一个流下光滑度量不变的充要条件。哈密顿力学的情况则成为一个推论。

辛几何

　　 我们也可以用辛几何的语言表述李维尔定理。对于一个给定的系统，我们可以将特定哈密顿量 \( H \) 的相空间 \( (q^\mu, p_\mu) \) 视为一个配备了辛 2 型的流形 \( (M, \omega) \)，其中辛 2 型为： \[ \omega = dp_\mu \wedge dq^\mu.~ \] 我们的流形的体积形式是辛 2 型的顶外幂，这也只是上述相空间度量的另一种表示。

　　 在这个相空间辛流形上，我们可以定义由一个函数 \( f(q, p) \) 生成的哈密顿向量场 \( X_f \)： \[ X_f = \frac{\partial f}{\partial p_\mu} \frac{\partial}{\partial q^\mu} - \frac{\partial f}{\partial q^\mu} \frac{\partial}{\partial p_\mu}.~ \] 具体来说，当生成函数就是哈密顿量 \( H \) 本身时，即 \( f(q, p) = H \)，我们得到[8]： \[ X_H = \frac{\partial H}{\partial p_\mu} \frac{\partial}{\partial q^\mu} - \frac{\partial H}{\partial q^\mu} \frac{\partial}{\partial p_\mu} = \frac{dq^\mu}{dt} \frac{\partial}{\partial q^\mu} + \frac{dp^\mu}{dt} \frac{\partial}{\partial p_\mu} = \frac{d}{dt}.~ \] 在这种形式下，李维尔定理表明，体积形式在由 \( X_H \) 生成的流中，李导数为零。也就是说，对于一个 2n 维的辛流形 \( (M, \omega) \)， \[ \mathcal{L}_{X_H}(\omega^n) = 0.~ \] 事实上，辛结构 \( \omega \) 本身是保持不变的，而不仅仅是它的顶外幂。也就是说，李维尔定理还表明[9]： \[ \mathcal{L}_{X_H}(\omega) = 0.~ \]

量子李维尔方程

　　 量子力学中李维尔方程的类似物描述了混合态的时间演化。规范量子化法得到该定理的量子力学版本，即冯·诺依曼方程。这个过程通常用于构造经典系统的量子模拟，涉及用哈密顿力学描述一个经典系统。然后，将经典变量重新解释为量子算符，而泊松括号被换成对易子。在这种情况下，得到的方程为[10][11]： \[ \frac{\partial \rho}{\partial t} = \frac{1}{i\hbar}[H, \rho],~ \] 其中，\( \rho \) 是密度矩阵。

　　 当应用于一个可观测量的期望值时，相应的方程由厄尔恩费斯特定理给出，形式为： \[ \frac{d}{dt} \langle A \rangle = -\frac{1}{i\hbar} \langle [H, A] \rangle,~ \] 其中，\( A \) 是一个可观测量。注意符号的差异，这源于假设算符是静止的，而态是时间依赖的。

　　 在量子力学的相空间表述中，将 Moyal 括号代替泊松括号应用于冯·诺依曼方程的相空间类比，导致概率流体的可压缩性，从而违反了李维尔定理的不可压缩性。因此，这也导致了在定义有意义的量子轨迹时的困难。[12]

3. 例子

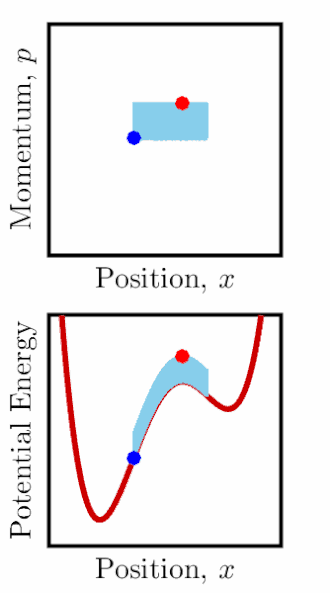
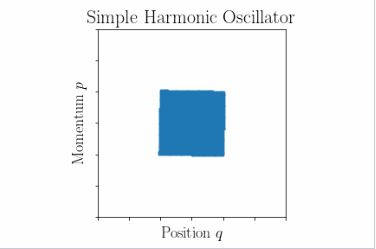
简谐振子（SHO）相空间体积

　　 考虑一个三维空间中的 \(N\) 颗粒系统，并仅关注 \(d\mathcal{N}\) 颗粒的演化。在相空间中，这些 \(d\mathcal{N}\) 颗粒占据一个由下式给出的无穷小体积： \[ d\Gamma = \prod_{i=1}^{N} d^3p_i \, d^3q_i~ \] 我们希望 \( \frac{d\mathcal{N}}{d\Gamma} \) 在时间上保持不变，以便 \( \rho(\Gamma, t) \) 沿系统的轨迹保持恒定。如果我们允许粒子经历一个无穷小的时间步长 \( \delta t \)，我们可以看到每个粒子的相空间位置变化如下： \[ \begin{cases} q_i' = q_i + \dot{q_i} \delta t, \\ p_i' = p_i + \dot{p_i} \delta t, \end{cases}~ \] 其中，\( \dot{q_i} \) 和 \( \dot{p_i} \) 分别表示 \( \frac{dq_i}{dt} \) 和 \( \frac{dp_i}{dt} \)，我们只保留了关于 \( \delta t \) 的线性项。扩展到我们的无穷小超立方体 \( d\Gamma \)，边长的变化为： \[ \begin{cases} dq_i' = dq_i + \frac{\partial \dot{q_i}}{\partial q_i} dq_i \delta t, \\ dp_i' = dp_i + \frac{\partial \dot{p_i}}{\partial p_i} dp_i \delta t. \end{cases}~ \] 为了求得新的无穷小相空间体积 \( d\Gamma' \)，我们需要这些量的乘积。到 \( \delta t \) 的一阶，我们得到以下结果： \[ dq_i' dp_i' = dq_i dp_i \left[1 + \left( \frac{\partial \dot{q_i}}{\partial q_i} + \frac{\partial \dot{p_i}}{\partial p_i} \right) \delta t \right].~ \] 到目前为止，我们还没有对系统做任何特定假设。现在我们假设 \( N \) 个 3 维各向同性简谐振子的情况。即，系统中的每个粒子可以视为一个简单的简谐振子。该系统的哈密顿量为： \[ H = \sum_{i=1}^{3N} \left( \frac{1}{2m} p_i^2 + \frac{m\omega^2}{2} q_i^2 \right).~ \] 利用上述哈密顿量和哈密顿方程，我们发现括号中的项恰好为零，从而得出： \[ dq_i' dp_i' = dq_i dp_i.~ \] 由此，我们可以得到相空间的无穷小体积： \[ d\Gamma' = \prod_{i=1}^{N} d^3q_i' d^3p_i' = \prod_{i=1}^{N} d^3q_i d^3p_i = d\Gamma.~ \] 因此，我们最终发现无穷小相空间体积保持不变，从而得到： \[ \rho(\Gamma', t + \delta t) = \frac{d\mathcal{N}}{d\Gamma'} = \frac{d\mathcal{N}}{d\Gamma} = \rho(\Gamma, t),~ \] 证明了李约维尔定理在该系统中的成立。[13]

　　 剩下的问题是相空间体积如何随时间演化。上面我们已经展示了总体积是守恒的，但没有说明它的具体形态。对于单个粒子，我们可以看到其在相空间中的轨迹是一个常量 \( H \) 的椭圆。通过显式解哈密顿方程，我们可以得到： \[ \begin{aligned} q_i(t) &= Q_i \cos\left(\omega t\right) + \frac{P_i}{m\omega} \sin\left(\omega t\right) , \\ p_i(t) &= P_i \cos\left(\omega t\right) - m\omega Q_i \sin\left(\omega t\right) , \end{aligned}~ \] 其中 \( Q_i \) 和 \( P_i \) 分别表示第 \(i\) 个粒子的初始位置和动量。对于多粒子系统，每个粒子都有一个相空间轨迹，描绘出与粒子能量对应的椭圆。椭圆的旋转频率由哈密顿量中的 \( \omega \) 给出，与能量的差异无关。因此，相空间的某个区域将围绕点 \( (\mathbf{q}, \mathbf{p}) = (0, 0) \) 旋转，旋转频率依赖于 \( \omega \)。

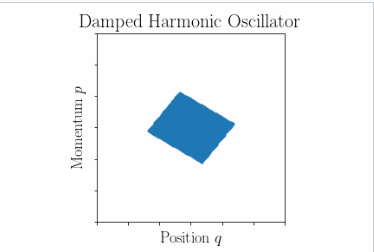
阻尼谐振子

　　 为了看到李奥维尔定理不适用的例子，我们可以修改简单谐振子的运动方程，以考虑摩擦或阻尼效应。再次考虑一个系统，其中每个粒子都在三维各向同性的谐振势中，其哈密顿量如前述示例所示。这次，我们加入一个条件，每个粒子都受到摩擦力 \( -\gamma p_i \) 的作用，其中 \( \gamma \) 是一个正的常数，决定了摩擦的大小。由于这是一个非保守力，我们需要扩展哈密顿方程为： \[ \begin{aligned} \dot{q}_i &= \frac{\partial H}{\partial p_i}, \\ \dot{p}_i &= -\frac{\partial H}{\partial q_i} - \gamma p_i. \end{aligned}~ \] 与简单谐振子的运动方程不同，这些修改后的方程不再是哈密顿方程的形式，因此我们不期望李奥维尔定理成立。相反，如本节动画所示，典型的相空间体积将在这些运动方程下收缩。

　　 为了明确看到李奥维尔定理的违反，我们可以按照与无阻尼谐振子类似的程序进行，并再次得到： \[ dq_i' dp_i' = dq_i dp_i \left[ 1 + \left( \frac{\partial^2 H}{\partial q_i \partial p_i} - \frac{\partial^2 H}{\partial p_i \partial q_i} - \gamma \right) \delta t \right],~ \] \[ = dq_i dp_i \left[ 1 - \gamma \delta t \right].~ \] 计算我们的新微小相空间体积，并仅保留 \( \delta t \) 的一阶项，我们得到如下结果： \[ \mathrm{d} \Gamma' = \prod_{i=1}^{N} d^3q_i' d^3p_i' = \left[ 1 - \gamma \delta t \right]^{3N} \prod_{i=1}^{N} d^3q_i d^3p_i = \mathrm{d} \Gamma \left[ 1 - 3N \gamma \delta t \right].~ \] 我们发现微小的相空间体积不再是常数，因此相空间密度不再守恒。可以从方程中看到，随着时间的推移，我们预计相空间体积会随着摩擦力的作用而减少至零。

　　 至于相空间体积如何随时间演化，我们仍然会像无阻尼情况下那样看到恒定的旋转。然而，阻尼会引入每个椭圆半径的持续减小。我们可以使用哈密顿方程显式地求解轨迹，注意使用上述修改后的方程。为了方便起见，设定 \( \alpha \equiv \frac{\gamma}{2} \)，我们得到： \[ \begin{aligned} q_i(t) &= e^{-\alpha t} \left[ Q_i \cos \omega_1 t + B_i \sin \omega_1 t \right], && \omega_1 \equiv \sqrt{\omega^2 - \alpha^2}, \\ p_i(t) &= e^{-\alpha t} \left[ P_i \cos \omega_1 t - m(\omega_1 Q_i + 2 \alpha B_i) \sin \omega_1 t \right], && B_i \equiv \frac{1}{\omega_1} \left( \frac{P_i}{m} + 2 \alpha Q_i \right), \end{aligned}~ \] 其中 \( Q_i \) 和 \( P_i \) 分别表示第 \( i \) 个粒子的初始位置和动量。随着系统的演化，总的相空间体积将螺旋式地收缩到原点。这可以从上图中看到。

4. 备注

　　 李欧维尔方程适用于平衡系统和非平衡系统。它是非平衡统计力学的一个基本方程。 李欧维尔方程是波动定理的证明中的关键部分，从中可以推导出热力学第二定律。它还是推导格林–库博关系的关键组成部分，格林–库博关系用于线性输运系数，如剪切粘度、热导率或电导率。 几乎任何一本关于哈密顿力学、先进统计力学或辛几何的教科书都会推导李欧维尔定理。[9][15][16][17][18] 在等离子体物理中，弗拉索夫方程可以解释为李欧维尔定理，这将解决弗拉索夫方程的任务简化为单粒子运动的问题。[19] 通过使用李欧维尔定理，例如在能量或磁矩守恒的条件下，可以利用已知的粒子分布函数确定未知的场，反之亦然。这种方法称为李欧维尔映射。[19]

5. 参见

• 波尔兹曼输运方程
• 可逆参考系统传播算法（r-RESPA）

6. 参考文献

1. Harald J. W. Müller-Kirsten, *Basics of Statistical Physics*, 2nd ed., World Scientific (Singapore, 2013)
2. Kubo, Ryogo (1963-02-01). "Stochastic Liouville Equations". *Journal of Mathematical Physics*, 4 (2): 174–183. Bibcode:1963JMP.....4..174K. doi:10.1063/1.1703941. ISSN 0022-2488.
3. J. W. Gibbs, "On the Fundamental Formula of Statistical Mechanics, with Applications to Astronomy and Thermodynamics." *Proceedings of the American Association for the Advancement of Science*, 33, 57–58 (1884). Reproduced in *The Scientific Papers of J. Willard Gibbs*, Vol II (1906), p. 16.
4. Gibbs, Josiah Willard (1902). *Elementary Principles in Statistical Mechanics*. New York: Charles Scribner's Sons.
5. Liouville, Joseph (1838). "Sur la Theorie de la Variation des constantes arbitraires" (PDF). *Journal de mathématiques pures et appliquées*, 3: 342–349.
6. Ehrendorfer, Martin. "The Liouville Equation: Background - Historical Background". *The Liouville Equation in Atmospheric Predictability* (PDF). pp. 48–49.
7. Harald J.W. Müller-Kirsten, *Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral*, 2nd ed., World Scientific (Singapore, 2012).
8. Nakahara, Mikio (2003). *Geometry, Topology, and Physics* (2 ed.). Taylor & Francis Group. pp. 201–204. ISBN 978-0-7503-0606-5.
9. Nash, Oliver (8 January 2015). "Liouville's theorem for pedants" (PDF). Proves Liouville's theorem using the language of modern differential geometry.
10. The Theory of Open Quantum Systems, by Breuer and Petruccione, p. 110.
11. Schwabl, *Statistical Mechanics*, p. 16.
12. Oliva, Maxime; Kakofengitis, Dimitris; Steuernagel, Ole (2018). "Anharmonic quantum mechanical systems do not feature phase space trajectories". *Physica A: Statistical Mechanics and Its Applications*, 502: 201–210. arXiv:1611.03303. Bibcode:2018PhyA..502..201O. doi:10.1016/j.physa.2017.10.047. S2CID 53691877.
13. Kardar, Mehran (2007). *Statistical Physics of Particles*. University of Cambridge Press. pp. 59–60. ISBN 978-0-521-87342-0.
14. Eastman, Peter (2014–2015). "Evolution of Phase Space Probabilities".
15. For a particularly clear derivation see Tolman, R. C. (1979). *The Principles of Statistical Mechanics*. Dover. pp. 48–51. ISBN 9780486638966.
16. "Phase Space and Liouville's Theorem". Retrieved January 6, 2014. Nearly identical to proof in this Wikipedia article. Assumes (without proof) the n-dimensional continuity equation.
17. "Preservation of phase space volume and Liouville's theorem". Retrieved January 6, 2014. A rigorous proof based on how the Jacobian volume element transforms under Hamiltonian mechanics.
18. "Physics 127a: Class Notes" (PDF). Retrieved January 6, 2014. Uses the n-dimensional divergence theorem (without proof).
19. Schwartz, S. J., Daly, P. W., and Fazakerley, A. N., 1998, *Multi-Spacecraft Analysis of Plasma Kinetics*, in *Analysis Methods for Multi-Spacecraft Data*, edited by G. Paschmann and P. W. Daly, no. SR-001 in ISSI Scientific Reports, chap. 7, pp. 159–163, ESA Publ. Div., Noordwijk, Netherlands.

7. 进一步阅读

• Murugeshan, R. *Modern Physics*. S. Chand.
• Misner, Charles W.; Thorne, Kip S.; Wheeler, John Archibald (1973). "Kinetic Theory in Curved Spacetime". *Gravitation*. Freeman. pp. 583–590. ISBN 9781400889099.

8. 外部链接

• "Phase space distribution functions and Liouville's theorem".