Matlab 解常微分方程组（ode45）

贡献者： addis

预备知识　Matlab 的函数，Matlab 画图

　　 Matlab 自带的 ode45 解算器使用成熟的变步长的 4 阶和 5 阶 Runge-Kutta 算法（该算法的简单实现详见）。

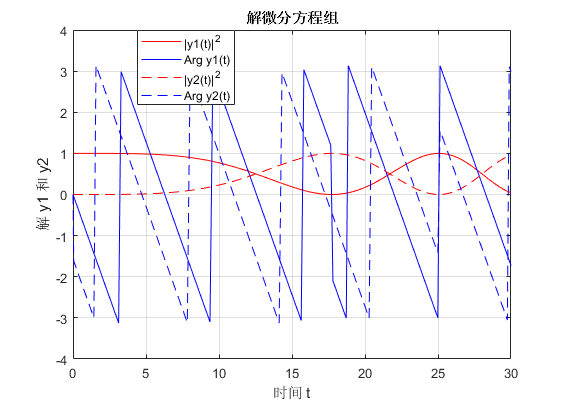
图 1：ode45_test.m 的运行结果。注意 $y_1$ 的相位在 $t=17$ 左右发生了一次反转，但此时模长为零，这代表 $y_1$ 在复平面上穿过了 $0$。$y_2$ 在 $t=25$ 穿过了 $0$。

　　下面我们演示如何用它求解一个简单的微分方程组的初值问题（结果如图 1 所示）。

\begin{equation} \left\{\begin{aligned} &\dot y_1 = - \mathrm{i} (y_1 + \alpha t y_2)~,\\ &\dot y_2 = - \mathrm{i} (\alpha t y_1 + y_2)~. \end{aligned}\right. \end{equation}

其中 $\alpha$ 为常数。为了告诉解算器我们需要求解的方程，我们要先定义一个数值函数

代码 1：odefun.m

function dydt = odefun(t, y, alpha)
    A = -1i*[1 alpha*t; alpha*t 1];
    dydt = A * y;
end

这里方程用矩阵乘法表示为

\begin{equation} \dot{ \boldsymbol{\mathbf{y}} (t)} = \boldsymbol{\mathbf{A}} (t) \boldsymbol{\mathbf{y}} (t)~. \end{equation}

表示为矩阵乘法只是为了方便而不是必须的——解算器无法看到这个函数内部是什么，只要输入某时刻的 $t$ 和 $ \boldsymbol{\mathbf{y}} (t)$ 时，输出正确的 $\dot{ \boldsymbol{\mathbf{y}} (t)}$ 即可。

　　接下来我们要把微分方程（odefun）和 $t$ 的求解范围（tspan），以及初始条件（$ \boldsymbol{\mathbf{y}} (0)$ 或 y0）告诉解算器。如果不想用两个 m 文件，可以把上面的 odefun() 函数的定义直接粘贴到 ode45_test.m 文件最后。

　　在解算器 ode45 的输出中，t 是一个 $1\times N$ 的递增数组，而 y 是一个 $2\times N$ 的矩阵，每一列对应 t 的一个值。这样就离散地表示出了函数 $ \boldsymbol{\mathbf{y}} (t_i)$。注意由于这是一个变步长解算器，t 并不是等间距的。

代码 2：ode45_test.m

function ode45_test
close all;

alpha = 0.01;  % 方程中的常数
y0 = [1; 0]; % 初始条件

% 时间跨度
tspan = [0 30];  % t 从 0 到 30

% 调用 ODE 求解器
[t, y] = ode45(@(t,y) odefun(t, y, alpha), tspan, y0);

% 绘制结果
figure;
plot(t, abs(y(:,1)).^2, 'r'); hold on; grid on;
plot(t, angle(y(:,1)), 'b');
plot(t, abs(y(:,2)).^2, 'r--');
plot(t, angle(y(:,2)), 'b--');
title('解微分方程组');
xlabel('时间 t');
ylabel('解 y1 和 y2');
legend({'|y1(t)|^2', 'Arg y1(t)', '|y2(t)|^2', 'Arg y2(t)'});
end

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。