麦克斯韦-玻尔兹曼统计（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在统计力学中，麦克斯韦–玻尔兹曼统计描述了经典物质粒子在热平衡中不同能级上的分布。当温度足够高或粒子密度足够低，以至于量子效应可以忽略不计时，这一统计方法适用。

　　 对于麦克斯韦–玻尔兹曼统计，能量为 \(\varepsilon_i\) 的粒子的期望数为： \[ \langle N_i \rangle = \frac{g_i}{e^{(\varepsilon_i - \mu) / kT}} = \frac{N}{Z} g_i e^{-\varepsilon_i / kT}~ \] 其中：

• \(\varepsilon_i\) 是第 \( i \) 个能级的能量，
• \( \langle N_i \rangle \) 是能量为 \( \varepsilon_i \) 的状态集合中粒子的平均数，
• \( g_i \) 是第 \( i \) 个能级的简并度，即具有能量 \( \varepsilon_i \) 的状态的数量，这些状态可以通过其他方式加以区分[注 1]，
• \( \mu \) 是化学势，
• \( k \) 是玻尔兹曼常数，
• \( T \) 是绝对温度，
• \( N \) 是总粒子数： \[ N = \sum_i N_i~ \]
• \( Z \) 是配分函数： \[ Z = \sum_i g_i e^{-\varepsilon_i / kT}~ \]
• \( e \) 是欧拉数。

　　 等效地，粒子数有时表示为： \[ \langle N_i \rangle = \frac{1}{e^{(\varepsilon_i - \mu) / kT}} = \frac{N}{Z} e^{-\varepsilon_i / kT}~ \] 其中，索引 \( i \) 现在指定了一个特定的状态，而不是所有能量为 \( \varepsilon_i \) 的状态集合，并且配分函数 \( Z \) 由以下式子给出： \[ Z = \sum_i e^{-\varepsilon_i / kT}~ \]

1. 历史

　　 麦克斯韦–玻尔兹曼统计源于麦克斯韦–玻尔兹曼分布，很可能是对基础技术的提炼。该分布最早由麦克斯韦于 1860 年根据启发式方法推导出来。后来，玻尔兹曼在 1870 年代对该分布的物理起源进行了重要研究。该分布可以通过最大化系统熵的原理推导出来。

2. 与麦克斯韦–玻尔兹曼分布的关系

　　 麦克斯韦–玻尔兹曼分布和麦克斯韦–玻尔兹曼统计密切相关。麦克斯韦–玻尔兹曼统计是统计力学中的一个更为一般的原理，用于描述经典粒子处于特定能量状态的概率： \[ P_i = \frac{e^{-E_i / k_B T}}{Z}~ \] 其中：

• \( Z \) 是配分函数： \[ Z = \sum_i e^{-E_i / k_B T}~ \]
• \( E_i \) 是状态 \( i \) 的能量，
• \( k_B \) 是玻尔兹曼常数，
• \( T \) 是绝对温度。

　　 麦克斯韦–玻尔兹曼分布是麦克斯韦–玻尔兹曼统计在气体粒子动能上的具体应用。理想气体中粒子速度（或速率）的分布可以从统计假设推导得出，该假设认为气体分子的能级由其动能给出： \[ f(v) = \left( \frac{m}{2 \pi k_B T} \right)^{3/2} 4 \pi v^2 e^{-\frac{m v^2}{2 k_B T}}~ \] 其中：

• \( f(v) \) 是粒子速度的概率密度函数，
• \( m \) 是粒子的质量，
• \( k_B \) 是玻尔兹曼常数，
• \( T \) 是绝对温度，
• \( v \) 是粒子的速度。

推导

　　 我们可以从麦克斯韦–玻尔兹曼统计推导出麦克斯韦–玻尔兹曼分布，首先从麦克斯韦–玻尔兹曼的能级概率出发，并将动能 \( E = \frac{1}{2} m v^2 \) 代入，来将概率表示为速度的函数： \[ P(E) = \frac{1}{Z} \exp \left( \frac{-E}{k_B T} \right) \rightarrow P(v) = \frac{1}{Z} \exp \left( \frac{-m v^2}{2 k_B T} \right)~ \] 在三维空间中，这与球面面积成正比，\( 4 \pi v^2 \)。因此，速度 \( v \) 的概率密度函数（PDF）变为： \[ f(v) = C \cdot 4 \pi v^2 \exp \left( -\frac{m v^2}{2 k_B T} \right)~ \] 为了找到归一化常数 \( C \)，我们要求概率密度函数对所有可能速度的积分为 1： \[ \int_0^\infty f(v) dv = 1 \quad \rightarrow \quad C \int_0^\infty 4 \pi v^2 \exp \left( -\frac{m v^2}{2 k_B T} \right) dv = 1~ \] 通过使用已知的积分结果： \[ \int_0^\infty v^2 e^{-a v^2} dv = \frac{\sqrt{\pi}}{4 a^{3/2}}~ \] 其中 \( a = \frac{m}{2 k_B T} \)，我们得到： \[ C \cdot 4 \pi \cdot \frac{\sqrt{\pi}}{4 \left( \frac{m}{2 k_B T} \right)^{3/2}} = 1 \quad \rightarrow \quad C = \left( \frac{m}{2 \pi k_B T} \right)^{3/2}~ \] 因此，麦克斯韦–玻尔兹曼速度分布为： \[ f(v) = \left( \frac{m}{2 \pi k_B T} \right)^{3/2} 4 \pi v^2 \exp \left( -\frac{m v^2}{2 k_B T} \right)~ \]

3. 适用性

　　 麦克斯韦–玻尔兹曼统计用于推导理想气体的麦克斯韦–玻尔兹曼分布。然而，它也可以用于将该分布扩展到具有不同能量–动量关系的粒子，如相对论性粒子（从而得到麦克斯韦–尤特纳分布），以及扩展到非三维空间。

　　 麦克斯韦–玻尔兹曼统计通常被描述为 “可区分” 的经典粒子的统计方法。换句话说，粒子 \(A\) 处于状态 1 且粒子 \(B\) 处于状态 2 的配置与粒子 \(B\) 处于状态 1 且粒子 \(A\) 处于状态 2 的配置是不同的。这一假设导致了粒子在能量状态中的正确（玻尔兹曼）统计，但对于熵会产生不符合物理的结果，正如吉布斯悖论中所体现的那样。

　　 同时，实际上没有任何粒子具备麦克斯韦–玻尔兹曼统计所要求的特征。实际上，如果我们将某一类型的所有粒子（例如电子、质子、光子等）视为本质上不可区分的，那么吉布斯悖论就得以解决。一旦做出这一假设，粒子统计就发生了变化。在混合熵的例子中，熵的变化可以视为一个非广延熵的例子，这种变化源于两种类型粒子混合时的可区分性。

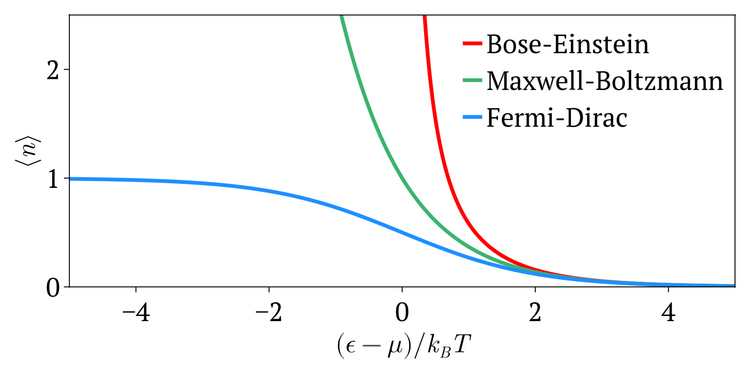
　　 量子粒子要么是玻色子（遵循玻色–爱因斯坦统计），要么是费米子（遵循费米–狄拉克统计，受保利排斥原理的约束）。这两种量子统计在高温和低粒子密度的极限下都会趋近于麦克斯韦–玻尔兹曼统计。

4. 推导

　　 麦克斯韦–玻尔兹曼统计可以在各种统计力学热力学集合中推导得出：\(^\text{[1]}\)

• 从大正则集合精确推导。
• 从正则集合精确推导。
• 从微正则集合推导，但仅在热力学极限下有效。

　　 在每种情况下，都必须假设粒子是非相互作用的，并且多个粒子可以占据相同的状态，并且是独立的。

从微正则集合的推导

　　 假设我们有一个容器，其中包含大量具有相同物理特征（如质量、电荷等）非常小的粒子。我们称这个容器为系统。假设尽管这些粒子具有相同的属性，但它们是可区分的。例如，我们可以通过持续观察它们的轨迹，或通过在每个粒子上做标记（例如，在每个粒子上画上不同的数字，就像在彩票球上做的那样）来识别每个粒子。

　　 这些粒子在容器内朝各个方向高速运动。由于粒子快速运动，它们拥有一定的能量。麦克斯韦–玻尔兹曼分布是一个数学函数，用来描述容器中有多少粒子具有某一特定能量。更准确地说，麦克斯韦–玻尔兹曼分布给出了与特定能量对应的状态被占据的非归一化概率（这意味着这些概率的总和不等于 1）。

　　 通常，可能有许多粒子具有相同的能量 \( \varepsilon \)。设具有相同能量 \( \varepsilon_1\) 的粒子数为 \( N_1 \)，具有另一个能量 \(\varepsilon_2 \) 的粒子数为 \(N_2\)，依此类推，对于所有可能的能量 \(\{\varepsilon_i \mid i = 1, 2, 3, \dots\}\)。为了描述这种情况，我们说 \( N_i \) 是能级 \(i\) 的占据数。

　　 如果我们知道所有的占据数 \(\{N_i \mid i = 1, 2,3,\dots\}\)，那么我们就知道系统的总能量。然而，因为我们可以区分哪些粒子占据了每个能级，所以占据数集合 \(\{N_i \mid i = 1, 2, 3, \dots\}\) 并不能完全描述系统的状态。为了完全描述系统的状态，或者说微观状态，我们必须准确地指定哪些粒子在每个能级上。因此，当我们计算系统可能的状态数时，我们必须计算每一个微观状态，而不仅仅是可能的占据数集合。

　　 首先，假设每个能级 \( i \) 只有一个状态（没有简并）。接下来是一些组合学思考，这与准确描述粒子库的状态关系不大。例如，假设总共有 \( k \) 个盒子，标记为 \( a, b, \dots, k \)。使用组合的概念，我们可以计算将 \( N \) 个粒子排列到这些盒子中的方式数，其中每个盒子内球的顺序不被追踪。首先，我们从 \( N \) 个粒子中选择 \( N_a \) 个放入盒子 \( a \)，然后继续为每个盒子从剩余的粒子中选择，确保每个粒子都放入一个盒子中。球的排列方式的总数是： \[ W = \frac{N!}{N_a!(N - N_a)!} \times \frac{(N - N_a)!}{N_b!(N - N_a - N_b)!} \times \frac{(N - N_a - N_b)!}{N_c!(N - N_a - N_b - N_c)!} \times \cdots \times \frac{(N - \cdots - N_\ell)!}{N_k!(N - \cdots - N_\ell - N_k)!}~ \] 简化后得到： \[ W = \frac{N!}{N_a! N_b! N_c! \cdots N_k!(N - N_a - \cdots - N_\ell - N_k)!}~ \] 由于每个球都已放入一个盒子中，\((N - N_a - N_b - \cdots - N_k)! = 0! = 1\)，我们可以简化表达式为： \[ W = N! \prod_{\ell = a,b,\ldots}^{k} \frac{1}{N_{\ell}!}~ \] 这正是多项式系数，表示将 \( N \) 个物品排列到 \( k \) 个盒子中的方式数，第 \( l \) 个盒子包含 \( N_l \) 个物品，忽略每个盒子内物品的排列。

　　 现在，考虑有多种方法将 \( N_i \) 个粒子放入盒子 \( i \) 的情况（即考虑简并性问题）。如果第 \( i \) 个盒子有一个 “简并度” \( g_i \)，即它有 \( g_i \) 个 “子盒子”（即有 \( g_i \) 个能量为 \( \varepsilon_i \) 的盒子，这些具有相同能量的状态/盒子被称为简并状态），那么每种填充第 \( i \) 个盒子的方法，其中子盒子中的数量发生变化，都是一种不同的填充方式。因此，填充第 \( i \) 个盒子的方式数必须增加 \( N_i \) 个物体在 \( g_i \) 个 “子盒子” 中的分布方式数。

　　 将 \(N_i\) 个可区分的物体放入 \(g_i\) 个 “子盒子” 中的方式数是 \(g_i^{N_i} \)（第一个物体可以放入任意一个 \(g_i\) 个盒子中，第二个物体也可以放入任意一个 \(g_i\) 个盒子中，依此类推）。因此，将总共 \( N \) 个粒子根据能量分类到能级中，并且每个能级 \(i\) 有 \( g_i\) 个不同状态，使得第 \(i\) 个能级容纳 \( N_i \) 个粒子的方式数 \(W\) 为： \[ W = N! \prod_{i} \frac{g_i^{N_i}}{N_i!}~ \] 这是玻尔兹曼首次推导出的 \(W\) 的形式。博尔兹曼的基本方程：\(S = k \ln W\) 将热力学熵 \( S \) 与微观状态数 \( W \) 相关联，其中 \( k \) 是玻尔兹曼常数。然而，吉布斯指出，上述 \( W \) 的表达式并不产生一个广延熵，因此是有缺陷的。这个问题被称为吉布斯悖论。问题在于，上述方程考虑的粒子是可区分的。换句话说，对于位于两个能量子级的两个粒子（\(A\) 和 \(B\)），由 \([A, B]\) 表示的人群被认为与由 \([B, A]\) 表示的人群不同，而对于不可区分的粒子，它们是不一样的。如果我们对不可区分的粒子进行推导，我们会得到 Bose–Einstein 形式的 \(W\)： \[ W = \prod_{i} \frac{(N_i + g_i - 1)!}{N_i!(g_i - 1)!}~ \] 当温度远高于绝对零度时，麦克斯韦-玻尔兹曼分布可以从玻色-爱因斯坦分布中推导出来，这意味着 \( g_i \gg 1 \)。麦克斯韦-玻尔兹曼分布还要求低密度，这意味着 \( g_i \gg N_i \)。在这些条件下，我们可以使用斯特林近似来计算阶乘： \[ N! \approx N^N e^{-N}~ \] 因此可以写成： \[ W \approx \prod_{i} \frac{(N_i + g_i)^{N_i + g_i}}{N_i^{N_i} g_i^{g_i}} \approx \prod_{i} \frac{g_i^{N_i} (1 + N_i / g_i)^{g_i}}{N_i^{N_i}}~ \] 利用 \( (1 + N_i / g_i)^{g_i} \approx e^{N_i} \)（对于 \( g_i \gg N_i \)）的事实，我们可以再次使用 Stirling 近似，得到： \[ W \approx \prod_{i} \frac{g_i^{N_i}}{N_i!}~ \] 这本质上是对玻尔兹曼原始表达式中的 \( N! \) 进行除法操作，这种修正被称为正确的玻尔兹曼计数。

　　 我们希望找到使函数 \(W\) 最大化的 \(N_i\)，同时考虑到固定的粒子数量 \((N = \sum N_i)\) 和固定的能量 \((E = \sum N_i \varepsilon_i)\) 的约束条件。\(W\) 和 \( \ln\left(W\right) \) 的最大值是由相同的 \(N_i\) 值实现的，并且由于数学上更容易操作，我们将最大化后者的函数。我们通过拉格朗日乘子法约束我们的解，构造如下的函数： \[ f(N_1, N_2, \dots, N_n) = \ln\left(W\right) + \alpha (N - \sum N_i) + \beta (E - \sum N_i \varepsilon_i)~ \] \[ \ln W = \ln \left[\prod_{i=1}^{n} \frac{g_i^{N_i}}{N_i!}\right] \approx \sum_{i=1}^{n} \left(N_i \ln g_i - N_i \ln N_i + N_i \right)~ \] 最后， \[ f(N_1, N_2, \dots, N_n) = \alpha N + \beta E + \sum_{i=1}^{n} \left( N_i \ln g_i - N_i \ln N_i + N_i - (\alpha + \beta \varepsilon_i) N_i \right)~ \] 为了最大化上述表达式，我们应用费马定理（驻点），根据该定理，如果存在局部极值，则必须位于临界点（偏导数为零）： \[ \frac{\partial f}{\partial N_i} = \ln g_i - \ln N_i - (\alpha + \beta \varepsilon_i) = 0~ \] 通过解上述方程（\(i = 1 \ldots n\)），我们得到关于 \(N_i\) 的表达式： \[ N_i = \frac{g_i}{e^{\alpha + \beta \varepsilon_i}}~ \] 将该表达式代入 \(\ln W\) 的方程，并假设 \(N \gg 1\)，我们得到： \[ \ln W = (\alpha + 1)N + \beta E~ \] 或者重新排列为： \[ E = \frac{\ln W}{\beta} - \frac{N}{\beta} - \frac{\alpha N}{\beta}~ \] 认识到这只是热力学基本方程的欧拉积分形式的一个表达式。将 \(E\) 识别为内能，欧拉积分基本方程表明： \[ E = TS - PV + \mu N~ \] 其中，\(T\) 是温度，\(P\) 是压力，\(V\) 是体积，\(\mu\) 是化学势。玻尔兹曼方程 \(S = k \ln W\) 实际上是熵与 \(\ln W\) 成正比，比例常数为玻尔兹曼常数的认识。利用理想气体状态方程（\(PV = NkT\)），可以立即得出：\( \beta = \frac{1}{kT} \quad \text{和} \quad \alpha = -\frac{\mu}{kT}\) 因此，粒子数目可以写为： \[ N_i = \frac{g_i}{e^{(\varepsilon_i - \mu) / (kT)}}~ \] 注意，上面的公式有时也可以写成： \[ N_i = \frac{g_i}{e^{\varepsilon_i / kT} / z}~ \] 其中，\(z = \exp\left(\mu / kT\right) \) 是绝对活度。

　　 另外，我们可以利用以下事实： \[ \sum_i N_i = N~ \] 来得到粒子数目为： \[ N_i = N \frac{g_i e^{-\varepsilon_i / kT}}{Z}~ \] 其中，\(Z\) 是配分函数，定义为： \[Z = \sum_i g_i e^{-\varepsilon_i / kT}~\] 在一个近似中，其中 \(\varepsilon_i\) 被认为是连续变量，托马斯–费米近似给出了一个与 \(\varepsilon\) 成正比的连续简并度 \(g\)，从而得到： \[ \frac{{\sqrt {\varepsilon }} \, e^{-\varepsilon / kT}}{\int_0^\infty {\sqrt {\varepsilon }} \, e^{-\varepsilon / kT}} = \frac{{\sqrt {\varepsilon }} \, e^{-\varepsilon / kT}}{\frac{{\sqrt {\pi}}}{2} (kT)^{3/2}} = \frac{{2 \sqrt {\varepsilon }} \, e^{-\varepsilon / kT}}{\sqrt {\pi (kT)^3}}~ \] 这就是能量的麦克斯韦–玻尔兹曼分布。

从正则系综推导

　　 在上述讨论中，玻尔兹曼分布函数是通过直接分析系统的多重性得到的。另一种方法是利用正则系综。在正则系综中，系统与一个热库处于热接触状态。虽然系统与热库之间可以自由交换能量，但假设热库具有无限大的热容量，从而保持整个系统的温度 \(T\) 恒定。

　　 在当前的情境下，假设我们的系统具有能级 \( \varepsilon_i \) 和简并度 \( g_i \)。与之前一样，我们希望计算系统具有能量 \( \varepsilon_i \) 的概率。

　　 如果我们的系统处于状态 \(s_1\)，那么热库对应的可用微态数量为 \(\Omega_R(s_1)\)。根据假设，整个系统（包括我们感兴趣的系统和热库）是孤立的，因此所有的微态都是等可能的。因此，例如，如果 \(\Omega_R(s_1) = 2 \Omega_R(s_2)\)，我们可以得出结论，系统处于状态 \(s_1 \) 的可能性是状态 \(s_2\) 的两倍。一般来说，如果 \(P(s_i)\) 是系统处于状态 \(s_i\) 的概率，则有： \[ \frac{P(s_1)}{P(s_2)} = \frac{\Omega_R(s_1)}{\Omega_R(s_2)}.~ \] 由于热库的熵 \( S_R = k \ln \Omega_R \)，上述关系变为： \[ \frac{P(s_1)}{P(s_2)} = \frac{e^{S_R(s_1)/k}}{e^{S_R(s_2)/k}} = e^{(S_R(s_1) - S_R(s_2))/k}.~ \] 接下来，我们回顾热力学恒等式（来自热力学第一定律）： \[ dS_R = \frac{1}{T}(dU_R + P\,dV_R - \mu\,dN_R).~ \] 在经典系综中，没有粒子的交换，因此 \( dN_R \) 项为零。同样，\( dV_R = 0 \)。这给出了： \[ S_R(s_1) - S_R(s_2) = \frac{1}{T} \left( U_R(s_1) - U_R(s_2) \right) = - \frac{1}{T} \left( E(s_1) - E(s_2) \right),~ \] 其中 \( U_R(s_i) \) 和 \( E(s_i) \) 分别表示热库和系统在状态 \( s_i \) 时的能量。对于第二个等式，我们使用了能量守恒。代入第一个关于 \( P(s_1), P(s_2) \) 的方程： \[ \frac{P(s_1)}{P(s_2)} = \frac{e^{-E(s_1)/kT}}{e^{-E(s_2)/kT}},~ \] 这意味着对于系统的任何状态 \( s \)，有： \[ P(s) = \frac{1}{Z} e^{-E(s)/kT},~ \] 其中 \( Z \) 是一个适当选择的 “常数”，用于使总概率为 1。（如果温度 \( T \) 不变，\( Z \) 是常数。） \[ Z = \sum_s e^{-E(s)/kT}.~ \] 其中索引 \( s \) 遍历系统的所有微观状态。\( Z \) 有时被称为态的玻尔兹曼求和（在原始德语中称为 "Zustandssumme"）。如果我们通过能量本征值而不是所有可能的状态来对求和进行索引，则必须考虑简并性。我们的系统具有能量 \( \varepsilon_i \) 的概率只是所有相应微观状态概率的总和： \[ P(\varepsilon_i) = \frac{1}{Z} g_i e^{-\varepsilon_i / kT}~ \] 其中，通过明显的修改， \[ Z = \sum_j g_j e^{-\varepsilon_j / kT},~ \] 这与之前的结果相同。

　　 关于这个推导的评论：

• 请注意，在这个公式中，最初的假设 “...假设系统具有总共 \( N \) 个粒子...” 被省略了。事实上，系统拥有的粒子数在得出分布时并不起作用。相反，多少粒子将占据具有能量 \( \varepsilon_i \) 的状态是一个简单的结果。
• 上述内容本质上是标准配分函数的推导。通过比较定义，可以看到态的 玻尔兹曼求和等于标准配分函数。
• 同样的方法可以用来推导费米-狄拉克和玻色–爱因斯坦统计。然而，在这些情况下，应将标准系综替换为大系综，因为系统和储备之间存在粒子交换。此外，在这些情况下，考虑的系统是一个单粒子状态，而不是粒子。（在上述讨论中，我们可以假设我们的系统是一个单一的原子。）

从规范系综的推导

　　 麦克斯韦-玻尔兹曼分布描述了在经典系统中粒子占据能量状态 E 的概率。它具有以下形式： \[ f_{\text{MB,high}}(E) = \exp \left( -\frac{E - E_F}{kT} \right), \quad \text{当} \, E \gg E_F~ \] \[ f_{\text{MB,low}}(E) = 1 - \exp \left( \frac{E - E_F}{kT} \right), \quad \text{当} \, E \ll E_F~ \] 对于不可区分的粒子系统，我们从规范系综的形式开始。

　　 在一个具有能量水平 \(\{E_i\}\) 的系统中，令 \(n_i\) 为处于第 \(i\) 状态的粒子数。总能量和粒子数分别为： \[ E_{\text{total}} = \sum_i n_i E_i~ \] \[ N = \sum_i n_i~ \] 对于一个特定的配置 \(\{n_i\}\)，在规范系综中的概率为： \[ P(\{n_i\}) = \frac{1}{Z_N} \frac{N!}{\prod_i n_i!} \prod_i (e^{-\beta E_i})^{n_i}~ \] 其中，因子 \(\frac{N!}{\prod_i n_i!}\) 用于计算将 \(N\) 个不可区分的粒子分布到各个状态的方式数。

　　 对于麦克斯韦-玻尔兹曼统计，我们假设任何状态的平均占据数远小于 1（\(\langle n_i \rangle \ll 1\)），这导致： \[ \langle n_i \rangle \approx e^{-\beta (E_i - \mu)}~ \] 其中，\(\mu\) 是化学势，由 \(\sum_i \langle n_i \rangle = N\) 决定。

　　 对于接近费米能量 \(E_F\) 的能级，我们可以表达 \(\mu \approx E_F\)，从而得到： \[ f_{\text{MB}}(E) = e^{-(E - E_F) / kT}~ \] 对于高能量（\(E \gg E_F\)），这直接得到： \[ f_{\text{MB,high}}(E) = e^{-(E - E_F) / kT}~ \] 对于低能量（\(E \ll E_F\)），使用近似 \(e^{-x} \approx 1 - x\)（当 \(x\) 很小时）： \[ f_{\text{MB,low}}(E) \approx 1 - e^{(E - E_F) / kT}~ \] 这就是在两种能量范围内推导麦克斯韦-玻尔兹曼分布的过程。

5. 参见

• 玻色-爱因斯坦统计
• 费米-狄拉克统计
• 玻尔兹曼因子

6. 注释

1. 例如，两个简单的点粒子可能具有相同的能量，但具有不同的动量矢量。它们可以基于这一点相互区分，简并度将是它们可以被区分的可能方式的数量。

7. 参考文献

1. Tolman, R. C. (1938). 《统计力学原理》. Dover Publications. ISBN 9780486638966.

8. 书目

• Carter, Ashley H.，《经典与统计热力学》，Prentice–Hall, Inc., 2001, 新泽西。
• Raj Pathria，《统计力学》，Butterworth–Heinemann, 1996。