玻色–爱因斯坦统计（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在量子统计学中，玻色–爱因斯坦统计（B–E 统计）描述了在热力学平衡下，一组非相互作用的相同粒子占据一组可用离散能级的两种可能方式之一。粒子聚集在同一状态中的现象是遵循玻色–爱因斯坦统计的粒子的特征，它解释了激光光束的凝聚流动和超流氦的无摩擦爬升。这一行为的理论由萨廷德拉·纳特·玻色于 1924-25 年提出，他认识到一组相同且不可区分的粒子可以以这种方式分布。这个想法后来被阿尔伯特·爱因斯坦与玻色合作进行了采纳和扩展。

　　 玻色–爱因斯坦统计仅适用于不遵循泡利不相容原理限制的粒子。遵循玻色–爱因斯坦统计的粒子称为玻色子，它们具有整数自旋。与此相对，遵循费米–狄拉克统计的粒子称为费米子，具有半整数自旋。

1. 玻色–爱因斯坦分布

图
图 1：具有整数自旋（玻色子）、半整数自旋（费米子）和经典（无自旋）粒子的热力学平衡分布。平均占据数 \(\langle n \rangle \) 显示为相对于系统化学势 \( \mu \) 的能量 \(\varepsilon\)，其中 \( T \) 是系统温度，\( k_B \) 是玻尔兹曼常数。

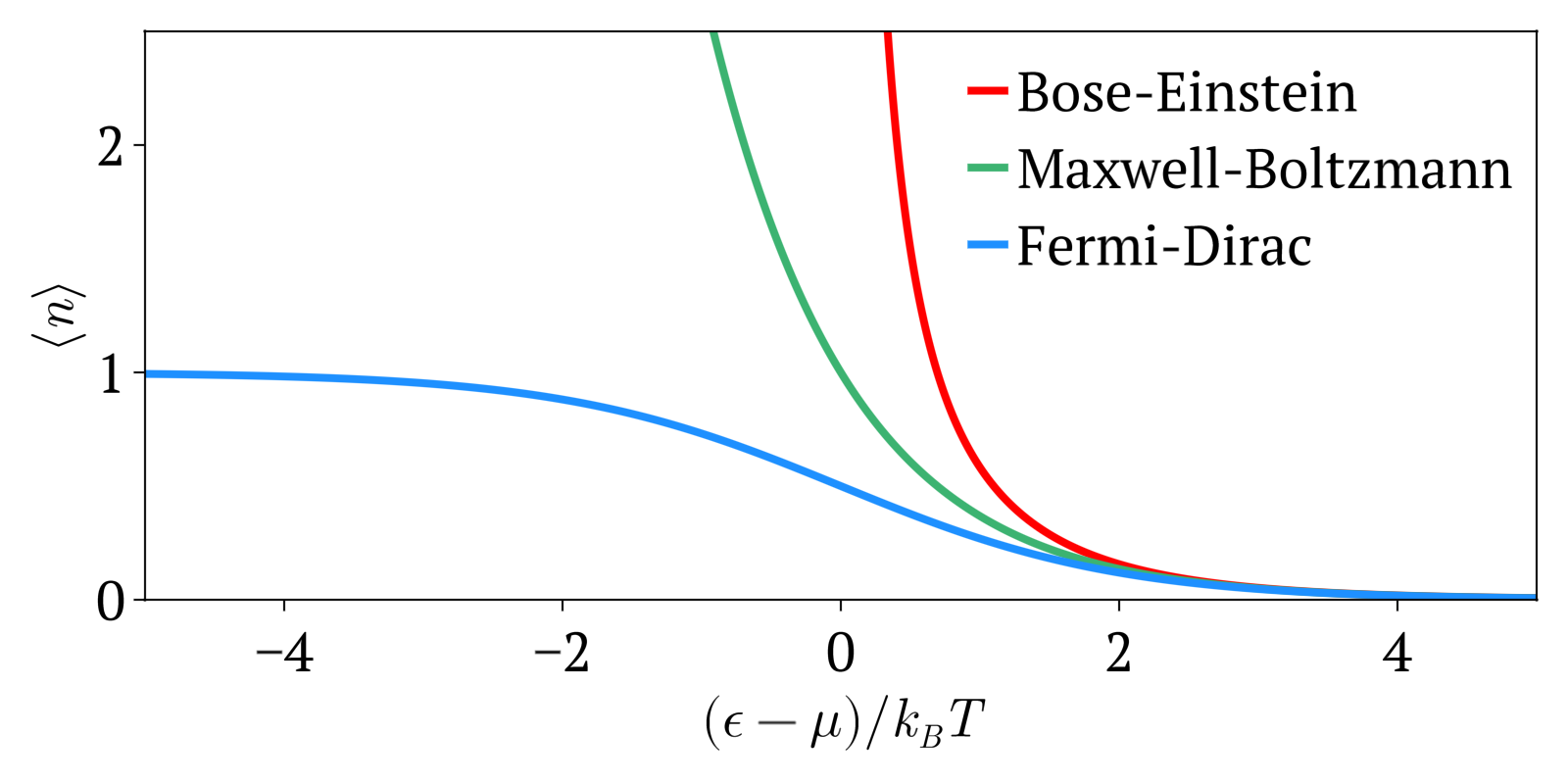
　　 在低温下，玻色子与费米子（遵循费米–狄拉克统计）表现不同，玻色子可以 “凝聚” 到相同的能级中，数量没有限制。这个看似不寻常的性质也导致了物质的特殊状态——玻色–爱因斯坦凝聚态。费米–狄拉克统计和玻色–爱因斯坦统计在量子效应重要且粒子 “不可区分” 时适用。如果粒子浓度满足 \[ \frac{N}{V} \geq n_{\text{q}},~ \] 其中 \( N \) 是粒子数，\( V \) 是体积，\( n_q \) 是量子浓度，对于量子浓度，粒子间的距离等于热德布罗意波长，因此粒子的波函数几乎不重叠。

　　 费米–狄拉克统计适用于费米子（遵循泡利不相容原理的粒子），而玻色–爱因斯坦统计适用于玻色子。由于量子浓度依赖于温度，大多数高温下的系统遵循经典（麦克斯韦–玻尔兹曼）极限，除非它们还具有非常高的密度，比如白矮星。无论是费米–狄拉克统计还是玻色–爱因斯坦统计，在高温或低浓度下都会变为麦克斯韦–玻尔兹曼统计。

　　 玻色–爱因斯坦统计由玻色于 1924 年引入用于光子，并在 1924–25 年由爱因斯坦推广到原子。

　　 玻色–爱因斯坦统计中，能级 \( i \) 中粒子的期望数为： \[ \bar{n}_i = \frac{g_i}{e^{(\varepsilon_i - \mu) / k_B T} - 1}~ \] 其中 \( \varepsilon_i > \mu \)，\( n_i \) 是状态 \( i \) 中的占据数（粒子数），\( g_i \) 是能级 \( i \) 的简并度，\( \varepsilon_i \) 是第 \( i \) 个状态的能量，\( \mu \) 是化学势（对于光子气体为零），\( k_B \) 是玻尔兹曼常数，\( T \) 是绝对温度。

　　 这个分布的方差 \( V(n) \) 直接从上面关于平均数的表达式计算得出。\(^\text{[1]}\) \[ V(n) = kT \frac{\partial}{\partial \mu} \bar{n}_i = \langle n \rangle (1 + \langle n \rangle) = \bar{n} + \bar{n}^2~ \] 为了比较，费米–狄拉克粒子-能量分布给出的能量为 \( \varepsilon_i \) 的费米子平均数具有类似的形式： \[ \bar{n}_i(\varepsilon_i) = \frac{g_i}{e^{(\varepsilon_i - \mu) / k_B T} + 1}.~ \] 如上所述，在高温和低粒子密度的极限下，玻色–爱因斯坦分布和费米–狄拉克分布都趋向于麦克斯韦–玻尔兹曼分布，而无需任何特别的假设：

　　 在低粒子密度的极限下，

　　 除了在高温 \( T \) 和低密度的极限下趋向于麦克斯韦–玻尔兹曼分布外，玻色–爱因斯坦统计还会在低能量状态下（当 \(\varepsilon_i - \mu \ll k_B T\) 时）简化为瑞利–金斯定律分布，即： \[ \bar{n}_i = \frac{g_i}{e^{(\varepsilon_i - \mu) / k_B T} - 1} \approx \frac{g_i}{(\varepsilon_i - \mu) / k_B T} = \frac{g_i k_B T}{\varepsilon_i - \mu}.~ \]

2. 历史

　　 瓦迪斯瓦夫·纳坦松在 1911 年得出结论，普朗克定律要求 “能量单位” 是不可区分的，尽管他并没有将这一点表述为爱因斯坦的光量子理论。\(^\text{[2][3]}\)

　　 在达卡大学（当时是英国印度的一部分，现在是孟加拉国）讲授辐射理论和紫外灾难时，萨廷德拉·纳特·玻色打算向他的学生展示，当时的理论是如何不足的，因为它预测的结果与实验结果不符。在这次讲座中，玻色在应用理论时犯了一个错误，这个错误出乎意料地给出了与实验一致的预测。这个错误是一个简单的失误——类似于认为抛两枚公平的硬币时会有三分之一的概率出现两个正面——对任何具有基本统计学知识的人来说，这个错误显然是错误的（值得注意的是，这个错误与 d'Alembert 在其《十字或正反面》一文中著名的失误类似 \(^\text{[4][5]}\)）。然而，它预测的结果与实验一致，玻色意识到这可能并非错误。第一次，他认为麦克斯韦–玻尔兹曼分布并不适用于所有尺度上的所有微观粒子。因此，他研究了在相空间中找到粒子处于各种状态的概率，其中每个状态是一个小的区域，具有相空间体积为 \( h^3 \)，粒子的位置和动量并没有特别分开，而是被视为一个变量。

　　 玻色将这次讲座改编成了一篇短文，名为《普朗克定律与光量子假说》\(^\text{[6][7]}\)，并将其提交给《哲学杂志》。然而，审稿人的报告是负面的，文章被拒绝了。玻色没有气馁，他将稿件寄给了阿尔伯特·爱因斯坦，请求在《物理学杂志》上发表。爱因斯坦立即同意，并亲自将文章从英语翻译成德语（玻色此前曾将爱因斯坦关于广义相对论的文章从德语翻译成英语），并确保文章顺利发表。玻色的理论获得了尊重，爱因斯坦在支持玻色的论文后，将自己的论文一同寄送到《物理学杂志》，要求它们一起发表。该论文于 1924 年发表 \(^\text{[8]}\)。

　　 玻色能够得出准确结果的原因是，由于光子是不可区分的，不能把具有相同量子数（如极化和动量向量）的两个光子视为两个不同的可识别光子。玻色最初在可能的自旋状态中有一个因子 2，但爱因斯坦将其改为极化 \(^\text{[9]}\)。通过类比，如果在另一个宇宙中硬币像光子和其他玻色子一样行为，那么产生两个正面的概率确实是三分之一，得到一正一反的概率则是传统（经典、可区分）硬币的一半。玻色的 “错误” 导致了现在称为玻色–爱因斯坦统计的理论。

　　 玻色和爱因斯坦将这个想法扩展到原子，并预测了后来被称为玻色–爱因斯坦凝聚的现象，这是一种密集的玻色子集合（玻色子是具有整数自旋的粒子，以玻色的名字命名），并于 1995 年通过实验证明了其存在。

3. 推导

　　 在微正则系综中，我们考虑一个具有固定能量、体积和粒子数的系统。我们假设系统由 \(N = \sum_i n_i\) 个相同的玻色子组成，其中 \(n_i\) 个粒子具有能量 \( \varepsilon_i\)，并分布在 \( g_i \) 个具有相同能量 \(\varepsilon_i\) 的能级或状态上，即 \( g_i \) 是与能量 \(\varepsilon_i\) 相关的简并度，系统的总能量为 \(E = \sum_i n_i \varepsilon_i\)。计算将 \( n_i\) 个粒子分布到 \( g_i\) 个状态中的排列数是一个组合学问题。由于在量子力学的背景下粒子是不可区分的，因此将 \( n_i \) 个粒子排列到 \( g_i \) 个盒子中（对于第 \( i \) 个能级）的方式数是（见图）：

图
图 2：该图表示玻色子粒子在不同盒子中的一种可能分布。盒子分隔（绿色）可以移动，以改变盒子的大小，从而改变每个盒子可以容纳的玻色子数。

　　 \[ w_{i,{\text{BE}}} = \frac{(n_{i}+g_{i}-1)!}{n_{i}!(g_{i}-1)!} = C_{n_{i}}^{n_{i}+g_{i}-1},~ \] 其中 \( C_{k}^{m} \) 是从 \( m \) 个元素中选取 \( k \) 个的组合数。玻色子系综中排列的总数简单地是上述二项式系数 \( C_{n_i}^{n_i+g_i-1} \) 在所有能级上的乘积，即： \[ W_{\text{BE}} = \prod_i w_{i,{\text{BE}}} = \prod_i \frac{(n_i + g_i - 1)!}{(g_i - 1)! n_i!}.~ \] 通过最大化熵（或等效地，设置 \(d(\ln W_{\text{BE}}) = 0\)），并考虑附加条件 \( N = \sum n_i \) 和 \( E = \sum_i n_i \varepsilon_i\)（作为拉格朗日乘子），可以得到对应的占据数 \(n_i\) 的最大排列数。\(^\text{[10]}\) 对于 \( n_i \gg 1 \)，\( g_i \gg 1\)，且 \( n_i / g_i = O(1) \)，结果就是玻色–爱因斯坦分布。

来自大正则系综的推导

　　 玻色–爱因斯坦分布仅适用于非相互作用的玻色子量子系统，它自然地从大正则系综中推导出来，而无需任何近似。\(\text{[11]}\) 在这个系综中，系统能够与一个储备库交换能量和粒子（储备库的温度 \(T\) 和化学势 \(\mu\) 被固定）。

　　 由于非相互作用的特性，每个可用的单粒子能级（具有能量 \(\varepsilon\)）形成一个与储备库接触的独立热力学系统。也就是说，整个系统中占据某个给定单粒子态的粒子数量形成了一个子系综，这个子系综也是大正则系综；因此，可以通过构造大配分函数来分析它。

　　 每个单粒子态具有固定的能量 \(\varepsilon\)。由于与单粒子态相关的子系综只随着粒子数的变化而变化，因此可以看出，子系综的总能量也与该单粒子态中的粒子数成正比；若 \(N\) 表示粒子数，则子系综的总能量为 \(N\varepsilon\)。从大配分函数的标准表达式出发，将总能量 \(E\) 替换为 \(N\varepsilon\)，大配分函数的形式如下： \[ \mathcal{Z} = \sum_{N} \exp\left((N\mu - N\varepsilon)/k_B T\right) = \sum_{N} \exp\left(N(\mu - \varepsilon)/k_B T\right)~ \]

　　 该公式适用于费米系统和玻色系统。费米–狄拉克统计的出现是由于考虑了泡利不相容原理的影响：虽然占据同一个单粒子态的费米子数只能是 0 或 1，但玻色子在一个单粒子态中的占据数可以是任意整数。因此，玻色子的配分函数可以被视为一个几何级数，并可以按此计算： \[ \mathcal{Z} = \sum_{N=0}^{\infty} \exp\left(N(\mu - \varepsilon)/k_B T\right) = \sum_{N=0}^{\infty} \left[\exp\left((\mu - \varepsilon)/k_B T\right)\right]^N = \frac{1}{1 - \exp\left((\mu - \varepsilon)/k_B T\right)}.~ \] 注意，这个几何级数仅当 \(e^{(\mu - \varepsilon)/k_B T} < 1\) 时才收敛，包括 \( \varepsilon = 0 \) 的情况。这意味着玻色气体的化学势必须为负，即：\(\mu < 0\),而费米气体的化学势则可以是正值或负值。\(^\text{[12]}\)

　　 对于该单粒子子态，平均粒子数为：

　　 \[ \langle N \rangle = k_{\text{B}} T \frac{1}{\mathcal{Z}} \left( \frac{\partial \mathcal{Z}}{\partial \mu} \right)_{V,T} = \frac{1}{\exp\left( (\varepsilon - \mu)/k_B T\right) - 1}~ \] 这个结果适用于每一个单粒子能级，因此构成了整个系统状态的玻色–爱因斯坦分布。\(^\text{[13][14]}\)

　　 粒子数的方差 \(\sigma_N^2 = \langle N^2 \rangle - \langle N \rangle^2\) 为： \[ \sigma_N^2 = k_{\text{B}} T \left( \frac{d \langle N \rangle}{d\mu} \right)_{V,T} = \frac{\exp\left( (\varepsilon - \mu)/k_B T\right)}{\left( \exp\left( (\varepsilon - \mu)/k_B T\right) - 1 \right)^2} = \langle N \rangle (1 + \langle N \rangle)~ \] 因此，对于高度占据的状态，能级的粒子数标准差非常大，略大于粒子数本身：\(\sigma_N \approx \langle N \rangle\).这种大的不确定性是由于给定能级中玻色子数目的概率分布是几何分布；有些反直觉的是，\( N \) 的最可能值始终为 0。（相比之下，经典粒子在给定状态下的粒子数服从泊松分布，具有更小的不确定性：\(\sigma_{N,{\text{classical}}} = \sqrt{\langle N \rangle}\) 且最可能的 \( N\) 值接近 \(\langle N \rangle\)。）

在正则系综中的推导

　　 也可以在正则系综中推导近似的玻色–爱因斯坦统计。这些推导较为繁琐，且只有在粒子数很大的渐近极限下才得到上述结果。原因在于，在正则系综中，玻色子的总数是固定的。在这种情况下，玻色–爱因斯坦分布可以像大多数教材中那样通过最大化来推导，但数学上最好的推导方法是通过达尔文–福勒的均值法，正如 Dingle 强调的那样。\(^\text{[15]}\) 另见 Müller-Kirsten。\(^\text{[10]}\) 然而，在凝聚区域中，基态的波动在正则系综和大正则系综中明显不同。\(^\text{[16]}\)

　　 推导

　　 假设我们有若干个能级，标记为索引 \(i\)，每个能级具有能量 \(\varepsilon_i \)，并包含总共 \(n_i\) 个粒子。假设每个能级包含 \(g_i\) 个不同的子能级，所有子能级具有相同的能量，并且是可区分的。例如，两个粒子可能具有不同的动量，在这种情况下，它们是可区分的，但它们仍然可以具有相同的能量。与能级 \(i\) 相关的 \(g_i\) 的值称为该能级的 “简并度”。任何数量的玻色子都可以占据同一个子能级。

　　 令 \(w(n, g)\) 表示将 \(n\) 个粒子分配到能级的 \(g\) 个子能级中的方式数。当只有一个子能级时，分配 \(n\) 个粒子只有一种方式，因此 \(w(n, 1) = 1\).很容易看出，将 \(n\) 个粒子分配到两个子能级的方式数是 \((n + 1)\)，我们可以写成： \[ w(n, 2) = \frac{(n+1)!}{n!1!}.~ \] 经过一些思考（见下方注释），可以看出将 \(n\) 个粒子分配到三个子能级的方式数为： \[ w(n, 3) = w(n, 2) + w(n-1, 2) + \cdots + w(1, 2) + w(0, 2),~ \] 因此， \[ w(n, 3) = \sum_{k=0}^{n} w(n-k, 2) = \sum_{k=0}^{n} \frac{(n-k+1)!}{(n-k)!1!} = \frac{(n+2)!}{n!2!}.~ \] 在这里，我们使用了以下涉及二项式系数的定理： \[ \sum_{k=0}^{n} \frac{(k+a)!}{k!a!} = \frac{(n+a+1)!}{n!(a+1)!}.~ \] 继续这个过程，我们可以看出 \(w(n, g)\) 只是一个二项式系数（见下方注释）： \[ w(n, g) = \frac{(n+g-1)!}{n!(g-1)!}.~ \] 例如，两个粒子在三个子能级中的占据数分别为 200、110、101、020、011 或 002，总共为六种方式，计算结果为 \( \frac{4!}{2!2!}\)。一组占据数 \(n_i \) 可以实现的方式数是每个能级可以被占据的方式数的乘积： \[ W = \prod_i w(n_i, g_i) = \prod_i \frac{(n_i + g_i - 1)!}{n_i!(g_i - 1)!} \approx \prod_i \frac{(n_i + g_i)!}{n_i!(g_i)!},~ \] 其中近似是基于 \(n_i \gg 1\) 的假设。

　　 按照推导麦克斯韦–玻尔兹曼统计的方法，我们希望找到一组 \(n_i\)，使得 \(W\) 最大化，同时满足粒子总数和总能量固定的约束条件。\(W\) 和 \( \ln\left(W\right) \) 的极值出现在相同的 \(n_i\) 值上，鉴于数学上更容易处理 \( \ln\left(W\right) \)，我们将最大化后者。我们使用拉格朗日乘子法对解进行约束，构造如下函数： \[ f(n_i) = \ln\left(W\right) + \alpha (N - \sum n_i) + \beta (E - \sum n_i \varepsilon_i)~ \] 利用 \(n_i \gg 1\) 的近似，并使用斯特林近似法对阶乘进行处理（\(x! \approx x^x e^{-x} \sqrt{2 \pi x}\)），得到： \[ f(n_i) = \sum_i (n_i + g_i) \ln\left(n_i + g_i\right) - n_i \ln\left(n_i\right) + \alpha (N - \sum n_i) + \beta (E - \sum n_i \varepsilon_i) + K,~ \] 其中 \(K\) 是一项不依赖于 \(n_i\) 的常数项。对 \(n_i\) 求导，将结果设为零，并解出 \(n_i\)，得到玻色–爱因斯坦人口数： \[ n_i = \frac{g_i}{e^{\alpha + \beta \varepsilon_i} - 1}.~ \] 通过类似于麦克斯韦–玻尔兹曼统计文章中概述的过程，可以看出： \[ d \ln W = \alpha \, dN + \beta \, dE~ \] 使用玻尔兹曼著名的关系 \(S = k_{\text{B}} \ln W\) 这一表达式变成了在恒定体积下热力学第二定律的陈述，从中可以推导出 \(\beta = \frac{1}{k_{\text{B}} T}\) 和 \(\alpha = -\frac{\mu}{k_{\text{B}} T}\)

　　 其中 \( S \) 是熵，\( \mu \) 是化学势，\( k_{\text{B}} \) 是玻尔兹曼常数，\( T \) 是温度，最终得到： \[ n_i = \frac{g_i}{e^{(\varepsilon_i - \mu)/k_{\text{B}} T} - 1}.~ \] 注意，上述公式有时也写作： \[ n_i = \frac{g_i}{e^{\varepsilon_i / k_{\text{B}} T} / z - 1},~ \] 其中 \( z = \exp\left(\mu / k_{\text{B}} T\right) \) 是绝对活度，正如 McQuarrie 所指出的。\(^\text{[17]}\)

　　 还需注意，当粒子数不守恒时，去除粒子数守恒约束相当于将 \( \alpha \) 和因此化学势 \( \mu \) 设为零。这适用于光子和在相互平衡中的有质量粒子，得到的分布将是普朗克分布。

　　 注释

　　 理解玻色–爱因斯坦分布函数的一个更简单的方法是：将 \( n \) 个粒子看作是相同的小球，将 \( g \) 个壳（能级）用 \( g - 1 \) 条线隔开。显然，将这 \( n \) 个小球与 \( g - 1 \) 条隔线进行不同的排列，就表示了将玻色子分布到不同能级的各种方式。例如，3 个粒子（\( n = 3 \)）和 3 个壳（\( g = 3 \)），因此有 \( g - 1 = 2 \) 条隔线，可能的排列方式包括：|●●|●，||●●●，|●|●●，等等。因此，对 \( n + (g - 1) \) 个物体（其中有 \( n \) 个相同的小球和 \( g - 1 \) 个相同的隔线）的不同排列方式数为： \[ \frac{(g - 1 + n)!}{(g - 1)! \, n!}~ \] 请参见图片，以直观地展示将 \( n \) 个粒子分配到 \( g \) 个盒子中的一种分布方式，该方式可以表示为 \( g - 1 \) 个分隔符。

图
图 3：这张图展示了玻色子粒子在不同盒子中的一种可能分布方式。盒子的隔板（绿色）可以移动，从而改变盒子的大小，进而影响每个盒子中可以容纳的玻色子数量。

　　 或者说：

　　 本注释旨在为初学者澄清玻色–爱因斯坦分布推导中的一些要点。玻色–爱因斯坦分布中的情况枚举（或排列方式）可以换一种方式来表述。考虑一个掷骰子的游戏，其中有 \( n \) 个骰子，每个骰子的取值范围为集合 \( \{1, \dots, g\} \)，其中 \( g \geq 1 \)。游戏的限制是，第 \( i \) 个骰子的点数（记作 \(m_i\) 必须大于或等于前一个骰子（第 \( i-1 \) 个，记作 \( m_{i-1}\) 的点数，即：\(m_i \geq m_{i-1}\).因此，一个合法的投掷序列可以表示为一个 n 元组 \((m_1, m_2, \dots, m_n)\),满足对所有 \( i = 1, \dots, n \)，都有 \( m_i \in \{1, \dots, g\} \) 且 \( m_i \geq m_{i-1} \)。令 \( S(n, g) \) 表示所有这样的合法 \(n\) 元组的集合： \[ S(n, g) = \left\{(m_1, m_2, \dots, m_n)\ \big|\ m_i \geq m_{i-1},\ m_i \in \{1, \dots, g\},\ \forall i = 1, \dots, n \right\}.~ \] 那么，上文定义的 \(w(n, g)\)（即将 \(n\) 个粒子分布到一个能级的 \(g\) 个子能级中的方式数），就等于集合 \(S(n, g)\) 的基数（即元素个数，或合法的 \(n\) 元组个数）。因此，求 \(w(n, g)\) 的问题就转化为计数集合 \(S(n, g)\) 中的元素个数的问题。

　　 例子：当 \( n = 4 \)，\( g = 3 \) 时： \[ S(4, 3) = \left\{ \underbrace{(1111), (1112), (1113)}_{(a)}, \underbrace{(1122), (1123), (1133)}_{(b)}, \underbrace{(1222), (1223), (1233), (1333)}_{(c)}, \underbrace{(2222), (2223), (2233), (2333), (3333)}_{(d)} \right\}~ \] \[ w(4, 3) = 15~ \] （集合 \( S(4, 3) \) 中共有 15 个元素）

　　 子集 \((a)\) 是通过将所有索引 \( m_i \) 固定为 1，除了最后一个索引 \( m_n\)，它从 1 增加到 \( g = 3 \) 得到的。子集 \((b)\) 是通过固定 \( m_1 = m_2 = 1 \)，并将 \( m_3 \) 从 2 递增到 \( g = 3 \) 得到的。根据集合 \( S(n, g) \) 中的约束条件 \( m_i \geq m_{i-1} \)，索引 \( m_4 \) 只能取值为 \( \{2, 3\} \)。子集 \((c)\) 和子集 \((d)\) 的构造方式与此类似。

　　 集合 \( S(4, 3) \) 中的每一个元素都可以看作是一个基数为 \( n = 4 \) 的多重集合；这个多重集合的元素取自集合 \( \{1, 2, 3\} \)，其基数为 \( g = 3 \)。这样的多重集合的数量等于以下的多重组合数： \[ \left\langle \begin{matrix} 3 \\ 4 \end{matrix} \right\rangle = \binom{3 + 4 - 1}{3 - 1}=\binom{3 + 4 - 1}{4}= \frac{6!}{4! \cdot 2!} = 15~ \] 更一般地说，集合 \( S(n, g) \) 中的每个元素都是一个基数为 \( n \) 的多重集合（可类比为 \( n \) 次投骰子的结果），其元素取自基数为 \( g \) 的集合 \( \{1, 2, \dots, g\} \)（可类比为每个骰子的可能取值）。这样的多重集合的总数，也就是 \( w(n, g) \)，等于以下的多重组合数： \[ w(n, g) = \left\langle \begin{matrix} g \\ n \end{matrix} \right\rangle = \binom{g + n - 1}{g - 1} = \binom{g + n - 1}{n} = \frac{(g + n - 1)!}{n! (g - 1)!}~ \] 这恰好与上文中通过一个涉及二项式系数的定理推导出的公式 \(w(n, g)\) 完全一致，即： \[ \sum_{k=0}^{n} \frac{(k + a)!}{k! \, a!} = \frac{(n + a + 1)!}{n! \, (a + 1)!}~ \] 为了理解如下的分解公式： \[ w(n, g) = \sum_{k = 0}^{n} w(n - k, g - 1) = w(n, g - 1) + w(n - 1, g - 1) + \cdots + w(1, g - 1) + w(0, g - 1)~ \] 例如，当 \( n = 4 \)、\( g = 3 \) 时，有： \[ w(4, 3) = w(4, 2) + w(3, 2) + w(2, 2) + w(1, 2) + w(0, 2)~ \] 我们可以按如下方式重新排列 \( S(4, 3) \) 中的元素：

图
图 4

　　 显然，集合 \( S(4, 3) \) 中的子集 \( (\alpha) \) 与集合 \( S(4, 2) \) 相同，即： \[ S(4, 2) = \{ (1111), (1112), (1122), (1222), (2222) \}~ \] 通过删除集合 \( S(4, 3) \) 中子集 \( (\beta) \) 中的索引 \( m_4 = 3 \)（在图中以红色和双下划线标出），可以得到集合 \[ S(3, 2) = \{ (111), (112), (122), (222) \}.~ \] 换句话说，集合 \( S(4, 3) \) 中的子集 \( (\beta) \) 与集合 \( S(3, 2) \) 之间存在一一对应关系。我们写作： \[ (\beta) \longleftrightarrow S(3, 2).~ \] 类似地，很容易看出： \[ (\gamma) \longleftrightarrow S(2, 2) = \{ (11), (12), (22) \}~ \] \[ (\delta) \longleftrightarrow S(1, 2) = \{ (1), (2) \}~ \] \[ (\omega) \longleftrightarrow S(0, 2) = \{\} = \varnothing.~ \] 因此，我们可以写成： \[ S(4, 3) = \bigcup_{k = 0}^{4} S(4 - k, 2)~ \] 或者更一般地： \[ S(n, g) = \bigcup_{k = 0}^{n} S(n - k, g - 1)~ \] 由于集合 \( S(i, g - 1) \)，对于 \( i = 0, \dots, n \)，是互不相交的，因此我们得到： \[ w(n, g) = \sum_{k = 0}^{n} w(n - k, g - 1)~ \] 并且约定： \[ w(0, g) = 1, \forall g, \quad \text{和} \quad w(n, 0) = 1, \forall n.~ \] 继续这个过程，我们得到如下公式： \[ w(n, g) = \sum_{k_1 = 0}^{n} \sum_{k_2 = 0}^{n - k_1} w(n - k_1 - k_2, g - 2) = \sum_{k_1 = 0}^{n} \sum_{k_2 = 0}^{n - k_1} \cdots \sum_{k_g = 0}^{n - \sum_{j = 1}^{g - 1} k_j} w(n - \sum_{i = 1}^{g} k_i, 0).~ \] 使用上面约定 \((7)_2\)，我们得到公式： \[ w(n, g) = \sum_{k_1 = 0}^{n} \sum_{k_2 = 0}^{n - k_1} \cdots \sum_{k_g = 0}^{n - \sum_{j = 1}^{g - 1} k_j} 1.~ \] 记住，对于常数 \( q \) 和 \( p \)，我们有： \[ \sum_{k = 0}^{q} p = q \cdot p.~ \] 然后可以验证，(8) 和 (2) 给出了相同的结果，例如 \( w(4, 3) \)、\( w(3, 3) \)、\( w(3, 2) \) 等。

4. 跨学科应用

　　 作为一种纯概率分布，玻色–爱因斯坦分布已被应用于其他领域：

5. 参见

6. 注释

  1. Pearsall, Thomas (2020). *Quantum Photonics*, 第二版。物理学研究生教材。Springer. doi:10.1007/978-3-030-47325-9. ISBN 978-3-030-47324-2.
  2. Jammer, Max (1966). *The Conceptual Development of Quantum Mechanics*. McGraw-Hill. 第 51 页. ISBN 0-88318-617-9.
  3. Passon, Oliver; Grebe-Ellis, Johannes (2017-05-01). "Planck's Radiation Law, the Light Quantum, and the Prehistory of Indistinguishability in the Teaching of Quantum Mechanics". *European Journal of Physics*. 38 (3): 035404. arXiv:1703.05635. Bibcode:2017EJPh...38c5404P. doi:10.1088/1361-6404/aa6134. ISSN 0143-0807. S2CID 119091804.
  4. d'Alembert, Jean (1754). "Croix ou pile". *L'Encyclopédie* (法语). 第 4 卷.
  5. d'Alembert, Jean (1754). "Croix ou pile" (PDF). Xavier University. 由 Richard J. Pulskamp 翻译. 2019 年 1 月 14 日访问.
  6. 参见论文第 14 页，注释 3：Michelangeli, Alessandro (2007 年 10 月). *Bose–Einstein Condensation: Analysis of Problems and Rigorous Results* (PDF) (博士学位论文). 高等研究院国际学校. 2018 年 11 月 3 日从原始文档归档. 2019 年 2 月 14 日访问.
  7. Bose (1924 年 7 月 2 日). "Planck's Law and the Hypothesis of Light Quanta" (PostScript). 奥尔登堡大学. 访问日期。
  8. Bose (1924), "Plancks Gesetz und Lichtquantenhypothese", *Zeitschrift für Physik* (德语), 26 (1): 178–181, Bibcode:1924ZPhy...26..178B, doi:10.1007/BF01327326, S2CID 186235974
  9. Ghose, Partha (2023). "The Story of Bose, Photon Spin and Indistinguishability". arXiv:2308.01909 [physics.hist-ph].
  10. H. J. W. Müller-Kirsten, *Basics of Statistical Physics*, 第二版, World Scientific (2013), ISBN 978-981-4449-53-3.
  11. Srivastava, R. K.; Ashok, J. (2005). "第 7 章". *Statistical Mechanics*. 新德里: PHI Learning Pvt. Ltd. ISBN 9788120327825.
  12. Landau, L. D., Lifšic, E. M., Lifshitz, E. M., & Pitaevskii, L. P. (1980). *Statistical Physics* (第 5 卷). Pergamon Press.
  13. "第 6 章". *Statistical Mechanics*. PHI Learning Pvt. 2005 年 1 月. ISBN 9788120327825.
  14. 玻色–爱因斯坦分布也可以从热场理论中推导出来。
  15. R. B. Dingle, *Asymptotic Expansions: Their Derivation and Interpretation*, Academic Press (1973), 第 267–271 页.
  16. Ziff R. M.; Kac, M.; Uhlenbeck, G. E. (1977). "The ideal Bose–Einstein gas, revisited". *Physics Reports* 32: 169–248.
  17. 参见 McQuarrie 引用文献。
  18. Amati, G.; C. J. Van Rijsbergen (2002). "基于衡量偏离随机性的概率模型的信息检索". *ACM TOIS* 20(4):357–389.
  19. Bianconi, G.; Barabási, A.-L. (2001). "复杂网络中的玻色–爱因斯坦凝聚". *Physical Review Letters* 86: 5632–5635.

7. 参考文献


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利