格罗斯–皮塔耶夫斯基方程（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 格罗斯–皮塔耶夫斯基方程（Gross–Pitaevskii equation，简称 GPE，以尤金·P·格罗斯和列夫·彼得罗维奇·皮塔耶夫斯基命名）在哈特里–福克近似与伪势相互作用模型的基础上，用来描述由相同玻色子组成的量子体系的基态。

　　 玻色–爱因斯坦凝聚是指一类玻色子气体，其所有粒子处于同一个量子态中，因此可以由相同的波函数描述。一个自由量子粒子可由单粒子薛定谔方程描述。对于现实气体中粒子间的相互作用，则需使用多体薛定谔方程加以考虑。在哈特里–福克近似中，整个由 $N$ 个玻色子组成的体系的总波函数 $\Psi$ 被认为是单粒子波函数 $\psi$ 的乘积： $$ \Psi(\mathbf{r}_1, \mathbf{r}_2, \dots, \mathbf{r}_N) = \psi(\mathbf{r}_1)\psi(\mathbf{r}_2) \dots \psi(\mathbf{r}_N)~ $$ 其中，$\mathbf{r}_i$ 是第 $i$ 个玻色子的坐标。如果气体中粒子之间的平均间距大于散射长度（即处于所谓的稀薄极限），那么可以用伪势来近似表示方程中真实的相互作用势能。在足够低的温度下，德布罗意波长远大于玻色子之间相互作用的作用范围，\(^\text{[3]}\) 此时的散射过程可以很好地用 s 波散射（即偏波分析中的 $\ell = 0$，也称为硬球势）来近似描述。在这种情况下，该体系的伪势模型哈密顿量可以写为： $$ H = \sum_{i=1}^{N} \left( -\frac{\hbar^2}{2m} \frac{\partial^2}{\partial \mathbf{r}_i^2} + V(\mathbf{r}_i) \right) + \sum_{i< j} \frac{4\pi \hbar^2 a_s}{m} \delta(\mathbf{r}_i - \mathbf{r}_j)~ $$

　　 其中，$m$ 是玻色子的质量，$V$ 是外部势，$a_s$ 是玻色子之间的 s 波散射长度，$\delta(\mathbf{r})$ 是狄拉克 δ 函数。

　　 变分法表明，如果单粒子波函数满足以下格罗斯–皮塔耶夫斯基方程： $$ \left(-\frac{\hbar^2}{2m} \frac{\partial^2}{\partial \mathbf{r}^2} + V(\mathbf{r}) + \frac{4\pi \hbar^2 a_s}{m} |\psi(\mathbf{r})|^2 \right) \psi(\mathbf{r}) = \mu \psi(\mathbf{r})~ $$ 那么总波函数在满足归一化条件 $\int dV\,|\Psi|^2 = N$ 的前提下，可以最小化该模型哈密顿量的期望值。因此，这样的单粒子波函数描述了体系的基态。

　　 格罗斯–皮塔耶夫斯基方程（GPE）是描述玻色–爱因斯坦凝聚态中基态单粒子波函数的模型方程。它在形式上类似于金兹堡–朗道方程，有时也被称为非线性薛定谔方程。

　　 格罗斯–皮塔耶夫斯基方程的非线性性来源于粒子之间的相互作用：若将该方程中的相互作用耦合常数设为零（见下一节），便可还原为描述陷阱势中单个粒子的线性薛定谔方程。

　　 通常认为格罗斯–皮塔耶夫斯基方程适用于弱相互作用区域。尽管如此，即使在该区域内，它有时也无法再现某些重要的物理现象。\(^\text{[4][5]}\) 若要研究超出弱相互作用极限的玻色–爱因斯坦凝聚体，则需要引入李–黄–杨修正项。\(^\text{[6][7]}\) 或者，在一维系统中，可以使用精确方法，例如 Lieb–Liniger 模型，\(^\text{[8]}\) 或使用扩展形式的方程，例如 Lieb–Liniger–Gross–Pitaevskii 方程，\(^\text{[9]}\)（有时也被称为修正的 \(^\text{[10]}\) 或广义的非线性薛定谔方程 \(^\text{[11]}\)）。

1. 方程形式

　　 该方程具有薛定谔方程的形式，但多了一个相互作用项。耦合常数 $g$ 与两个相互作用玻色子的 s 波散射长度 $a_s$ 成正比： $$ g = \frac{4\pi \hbar^2 a_s}{m}~ $$ 其中 $\hbar$ 是约化普朗克常数，$m$ 是玻色子的质量。

　　 能量密度为： $$ \mathcal{E} = \frac{\hbar^2}{2m} |\nabla \Psi(\mathbf{r})|^2 + V(\mathbf{r}) |\Psi(\mathbf{r})|^2 + \frac{1}{2} g |\Psi(\mathbf{r})|^4~ $$ 其中 $\Psi$ 是波函数（或称序参量），$V$ 是外部势（例如谐振势）。对于粒子数守恒的系统，其定态格罗斯–皮塔耶夫斯基方程为： $$ \mu \Psi(\mathbf{r}) = \left( -\frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r}) + g |\Psi(\mathbf{r})|^2 \right) \Psi(\mathbf{r})~ $$ 其中 $\mu$ 是化学势，它由以下条件确定，即粒子数 $N$ 与波函数之间的关系为： $$ N = \int |\Psi(\mathbf{r})|^2 \, d^3 r~ $$ 通过定态格罗斯–皮塔耶夫斯基方程，我们可以求解玻色–爱因斯坦凝聚体在不同外部势（例如谐振势）下的结构。

　　 时间依赖的格罗斯–皮塔耶夫斯基方程为： $$ i\hbar \frac{\partial \Psi(\mathbf{r}, t)}{\partial t} = \left( -\frac{\hbar^2}{2m} \nabla^2 + V(\mathbf{r}) + g |\Psi(\mathbf{r}, t)|^2 \right) \Psi(\mathbf{r}, t).~ $$ 通过这个方程，我们可以研究玻色–爱因斯坦凝聚体的动力学行为。它常被用来分析陷阱中的气体的集体激发模式。

2. 解的情况

　　 由于格罗斯–皮塔耶夫斯基方程是一个非线性偏微分方程，因此其精确解很难求得。因此，通常需要通过各种近似方法来求解。

精确解

　　 自由粒子情形

　　 最简单的精确解是自由粒子解，对应于外势为零，即 $V(\mathbf{r}) = 0$： $$ \Psi(\mathbf{r}) = \sqrt{\frac{N}{V}} e^{i\mathbf{k} \cdot \mathbf{r}}.~ $$ 这个解通常被称为哈特里解。虽然它确实满足格罗斯–皮塔耶夫斯基方程，但由于粒子间的相互作用，它会在能谱中留下一个能隙： $$ E(\mathbf{k}) = N\left[ \frac{\hbar^2 k^2}{2m} + g \frac{N}{2V} \right].~ $$ 根据 Hugenholtz–Pines 定理 \(^\text{[12]}\)，在存在排斥相互作用的情况下，相互作用的玻色气体不应出现能隙。

　　 孤子

　　 在一维玻色–爱因斯坦凝聚体中可以形成孤子。根据粒子间相互作用是吸引的还是排斥的，可以形成明孤子或暗孤子。这两种孤子都是凝聚体中在均匀背景密度上的局域扰动。

　　 如果玻色–爱因斯坦凝聚体具有排斥性相互作用，即 $g > 0$，那么格罗斯–皮塔耶夫斯基方程的一个可能解为： $$ \psi(x) = \psi_0 \tanh\left( \frac{x}{\sqrt{2} \, \xi} \right),~ $$ 其中 $\psi_0$ 是在无穷远处凝聚体波函数的取值，$\xi = \hbar/\sqrt{2 m n_0 g} = 1/\sqrt{8\pi a_s n_0}$ 是相干长度（也称为愈合长度，[3] 见下文）。该解表示暗孤子，因为在本应具有非零密度的空间中存在凝聚体的密度缺失。暗孤子也是一种拓扑缺陷，因为波函数 $\psi$ 在原点附近从正值跃变为负值，伴随着 $\pi$ 相位的突变。

　　 如果相互作用为吸引性，即 $g < 0$，则解为： $$ \psi(x, t) = \psi(0) e^{-i\mu t / \hbar} \frac{1}{\cosh\left( \sqrt{2m|\mu|/\hbar^2} x \right)},~ $$ 其中化学势为 $\mu = g |\psi(0)|^2/2$。这个解表示明孤子，因为在原本真空的空间中出现了凝聚体的局域集聚。

愈合长度

　　 愈合长度表示序参量（即凝聚体波函数）得以恢复的最小距离，用来描述玻色–爱因斯坦凝聚体（BEC）的波函数在多快的尺度上能对势能的变化作出调整。如果凝聚体的密度在距离 $\xi$ 内从 0 增长到 $n$，则可以通过量子压强与相互作用能相等来计算愈合长度：\(^\text{[3][13]}\) $$ \frac{\hbar^2}{2m \xi^2} = gn \quad \Longrightarrow \quad \xi = \left(8\pi n a_s\right)^{-1/2}~ $$ 愈合长度必须远小于单粒子波函数解中涉及的任何特征长度尺度。

　　 愈合长度还决定了超流体中所能形成的涡旋的尺度。它描述的是波函数在涡旋中心从零恢复到超流体主体部分取值所需的距离（因此被称为 “愈合” 长度）。

变分解法

　　 在一些无法获得精确解析解的系统中，可以采用变分近似的方法。其基本思想是为波函数构造一个包含自由参数的变分猜测，将其代入自由能表达式中，然后对这些自由参数进行能量最小化。

数值解法

　　 目前已有多种数值方法被用于求解格罗斯–皮塔耶夫斯基方程，例如分步 Crank–Nicolson 方法 \(^\text{[14]}\) 和 傅里叶谱方法 \(^\text{[15]}\)。此外，也有用于处理接触相互作用 \(^\text{[16][17]}\) 和长程偶极相互作用 \(^\text{[18]}\) 的不同 Fortran 和 C 语言程序实现。

托马斯–费米近似

　　 当气体中粒子数非常大时，原子间的相互作用变得很强，此时在格罗斯–皮塔耶夫斯基方程中可以忽略动能项。这种近似被称为托马斯–费米近似，在该近似下，单粒子波函数为： $$ \psi(x, t) = \sqrt{ \frac{ \mu - V(x) }{ N g } }.~ $$ 对应的密度分布为： $$ n(x, t) = \frac{ \mu - V(x) }{ g }.~ $$ 在谐振势阱中（即势能关于离开中心的位移是二次函数），这种形式的密度分布常被称为 “倒抛物线” 型密度分布。\(^\text{[3]}\)

玻戈留波夫近似

　　 对格罗斯–皮塔耶夫斯基方程进行玻戈留波夫处理是一种用于研究玻色–爱因斯坦凝聚体的基本激发态的方法。为此，将凝聚体的波函数近似表示为平衡态波函数与一个小扰动的和：$\psi_0 = \sqrt{n} \, e^{-i\mu t}, \quad \psi = \psi_0 + \delta \psi$ 其中 $\psi_0$ 是凝聚体在平衡状态下的波函数，$\delta \psi$ 是一个小扰动。

　　 将这一形式代入时间依赖的格罗斯–皮塔耶夫斯基方程及其共轭方程，并在线性近似下保留 $\delta \psi$ 的一阶项，得到以下线性化方程组： $$ i\hbar \frac{\partial \delta \psi}{\partial t} = -\frac{\hbar^2}{2m} \nabla^2 \delta \psi + V \delta \psi + g \left( 2|\psi_0|^2 \delta \psi + \psi_0^2 \delta \psi^* \right),~ $$

　　 $$ - i\hbar \frac{\partial \delta \psi^*}{\partial t} = -\frac{\hbar^2}{2m} \nabla^2 \delta \psi^* + V \delta \psi^* + g \left( 2|\psi_0|^2 \delta \psi^* + (\psi_0^*)^2 \delta \psi \right).~ $$ 这组方程描述了玻色–爱因斯坦凝聚体中由微小扰动引起的激发动力学行为。

　　 假设扰动项为： $$ \delta \psi = e^{-i\mu t} \left( u(\mathbf{r}) e^{-i\omega t} - v^*(\mathbf{r}) e^{i\omega t} \right),~ $$ 则可以通过将 $e^{\pm i\omega t}$ 视为独立分量，得到关于 $u$ 和 $v$ 的以下耦合微分方程： $$ \left( -\frac{\hbar^2}{2m} \nabla^2 + V + 2gn - \hbar \mu - \hbar \omega \right) u - gn v = 0,~ $$ $$ \left( -\frac{\hbar^2}{2m} \nabla^2 + V + 2gn - \hbar \mu + \hbar \omega \right) v - gn u = 0.~ $$ 对于均匀系统，即 $V(\mathbf{r}) = \text{常数}$，可以从零阶方程得到：$V = \hbar \mu - gn$ 接下来，我们假设 $u$ 和 $v$ 为动量为 $\mathbf{q}$ 的平面波，这将导出如下的能谱关系： $$ \hbar \omega = \epsilon_{\mathbf{q}} = \sqrt{ \frac{\hbar^2 |\mathbf{q}|^2}{2m} \left( \frac{\hbar^2 |\mathbf{q}|^2}{2m} + 2gn \right) }.~ $$ 当 $\mathbf{q}$ 较大时，这一色散关系呈二次型，这与非相互作用的单粒子激发行为相符；而当 $\mathbf{q}$ 较小时，色散关系为线性： $$ \epsilon_{\mathbf{q}} = s \hbar q,~ $$ 其中 $s = \sqrt{ng/m}$ 是凝聚体中的声速，也称为第二声速。根据朗道判据，由于 $\epsilon_{\mathbf{q}} / (\hbar q) > s$，这表明凝聚体是超流体：如果一个物体在凝聚体中以速度低于 $s$ 运动，那么激发激发态在能量上是不利的，也就是说不会产生能量耗散，物体将无阻力地运动，这是超流体的典型特性。已经通过实验验证了凝聚体的这种超流性，实验中使用的是紧聚焦的蓝失谐激光来激发。\(^\text{[19]}\) 当使用二次量子化形式主义从微观角度描述凝聚体时，也能得到相同的色散关系。

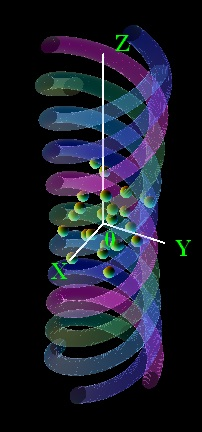
旋转螺旋势中的超流体

　　 光学势阱 $V_{\text{twist}}(\mathbf{r}, t) = V_{\text{twist}}(z, r, \theta, t)$ 可能由两个反向传播的光学涡旋形成，其波长分别为 $\lambda_{\pm} = \frac{2\pi c}{\omega_{\pm}}$，具有有效宽度 $D$ 和拓扑荷数 $\ell$。

　　 光场形式为： $$ E_{\pm}(\mathbf{r}, t) \sim \exp\left( -\frac{r^2}{2D^2} \right) r^{|\ell|} \exp\left( -i \omega_{\pm} t \pm i k_{\pm} z + i \ell \theta \right),~ $$ 其中 $\delta \omega = \omega_+ - \omega_-$ 是两个光学涡旋之间的频率差。在柱坐标系** $(z, r, \theta)$ 中，这种势阱呈现出显著的双螺旋几何结构。\(^\text{[20]}\) $$ V_{\text{twist}}(\mathbf{r}, t) \sim V_0 \exp\left(-\frac{r^2}{D^2}\right) r^{2|\ell|} \left(1 + \cos[\delta\omega t + (k_+ + k_-)z + 2\ell \theta] \right)~ $$ 在以角速度 $\Omega = \frac{\delta\omega}{2\ell}$ 旋转的参考系中，带有螺旋势的时间依赖格罗斯–皮塔耶夫斯基方程为：\(^\text{[21]}\) $$ i\hbar \frac{\partial \Psi(\mathbf{r}, t)}{\partial t} = \left( -\frac{\hbar^2}{2m} \nabla^2 + V_{\text{twist}}(\mathbf{r}) + g |\Psi(\mathbf{r}, t)|^2 - \Omega \hat{L} \right) \Psi(\mathbf{r}, t),~ $$ 其中 $\hat{L} = -i\hbar \frac{\partial}{\partial \theta}$ 是角动量算符。

　　 凝聚体波函数 $\Psi(\mathbf{r}, t)$ 的解为两个互为共轭相位的物质波涡旋的叠加态： $$ \Psi(\mathbf{r}, t) \sim \exp\left(-\frac{r^2}{2D^2}\right) r^{|\ell|} \left[ \exp\left(-i\omega_+ t + i k_+ z + i\ell \theta\right) + \exp\left(-i\omega_- t - i k_- z - i\ell \theta\right) \right].~ $$ 这个解展示了在旋转螺旋势场中超流体的螺旋涡旋结构与量子干涉特性。

　　 凝聚体在宏观上可观测的动量为： $$ \langle \Psi | \hat{P} | \Psi \rangle = N_{\text{at}} \hbar (k_+ - k_-),~ $$ 其中 $N_{\text{at}}$ 是凝聚体中的原子数。这意味着原子集体沿 $z$ 轴以群速度相干移动，其方向由拓扑荷数 $\ell$ 和角速度 $\Omega$ 的符号共同决定：\(^\text{[22]}\) $$ V_z = \frac{2 \Omega \ell}{k_+ + k_-}.~ $$ 而被螺旋势俘获的凝聚体的角动量严格为零：\(^\text{[21]}\) $$ \langle \Psi | \hat{L} | \Psi \rangle = N_{\text{at}} [\ell \hbar - \ell \hbar] = 0.~ $$ 对螺旋势中冷原子体系的数值模拟表明，单个原子的轨迹会被限制在螺旋势阱内部。\(^\text{[23]}\)

推导与推广

　　 格罗斯–皮塔耶夫斯基方程也可以通过以相干态表示的 s 波相互作用相同玻色子多体理论的半经典极限来推导得到。\(^\text{[24]}\) 在大量量子数的条件下达到半经典极限，此时可以将场论表述为正 P 表示（即广义的 Glauber–Sudarshan P 表示）或 Wigner 表示。

　　 有限温度效应可以通过广义格罗斯–皮塔耶夫斯基方程处理，其中包括凝聚态原子与非凝聚态原子之间的散射过程。\(^\text{[25][26][27][28][29]}\) 在低温极限下，可以从这种广义方程中恢复出标准的格罗斯–皮塔耶夫斯基方程。\(^\text{[30][31]}\)

3. 参考文献

1. E. P. Gross (1961). 《玻色子系统中量子化涡旋的结构》，*Il Nuovo Cimento*，20 (3): 454–457。Bibcode: 1961NCim...20..454G。doi: [10.1007/BF02731494](https://doi.org/10.1007/BF02731494)。S2CID: 121538191。
2. L. P. Pitaevskii (1961). 《非理想玻色气体中的涡旋线》，*Sov. Phys. JETP*，13 (2): 451–454。
3. Foot, C. J. (2005).《原子物理学》，牛津大学出版社，第 231–240 页。ISBN: 978-0-19-850695-9。
4. Raphael Lopes, Christoph Eigen, Nir Navon, David Clément, Robert P. Smith, Zoran Hadzibabic (2017 年 11 月 7 日). 《均匀玻色–爱因斯坦凝聚体中的量子耗尽》，*Physical Review Letters*，119 (19): 190404。arXiv:1706.01867。Bibcode: 2017PhRvL.119s0404L。doi: [10.1103/PhysRevLett.119.190404](https://doi.org/10.1103/PhysRevLett.119.190404)。PMID: 29219529。S2CID: 206302070。
5. R. Chang, Q. Bouton, H. Cayla, C. Qu, A. Aspect, C. I. Westbrook, D. Clément (2016 年 12 月 2 日). 《在玻色气体中对热耗尽与量子耗尽的动量分辨观测》，*Physical Review Letters*，117 (23): 235303。arXiv:1608.04693。Bibcode: 2016PhRvL.117w5303C。doi: [10.1103/PhysRevLett.117.235303](https://doi.org/10.1103/PhysRevLett.117.235303)。PMID: 27982640。S2CID: 10967623。
6. T. D. Lee, C. N. Yang（1957 年 2 月 1 日）.《量子力学与量子统计力学中的多体问题》（*Many-Body Problem in Quantum Mechanics and Quantum Statistical Mechanics*），《物理评论》（*Physical Review*），105 (3): 1119–1120。Bibcode: 1957PhRv..105.1119L。doi: [10.1103/PhysRev.105.1119](https://doi.org/10.1103/PhysRev.105.1119)。ISSN: 0031-899X。
7. T. D. Lee, Kerson Huang, C. N. Yang（1957 年 6 月 15 日）.《硬球玻色体系的本征值与本征函数及其低温性质》，《物理评论》，106 (6): 1135–1145。Bibcode: 1957PhRv..106.1135L。doi: [10.1103/PhysRev.106.1135](https://doi.org/10.1103/PhysRev.106.1135)。ISSN: 0031-899X。
8. Elliott H. Lieb, Werner Liniger（1963 年 5 月 15 日）.《相互作用玻色气体的精确分析：I. 通解与基态》，《物理评论》，130 (4): 1605–1616。Bibcode: 1963PhRv..130.1605L。doi: [10.1103/PhysRev.130.1605](https://doi.org/10.1103/PhysRev.130.1605)。ISSN: 0031-899X。
9. Jakub Kopyciński, Maciej Łebek, Maciej Marciniak, Rafał Ołdziejewski, Wojciech Górecki, Krzysztof Pawłowski（2022 年 1 月 14 日）.《一维气体中超越格罗斯–皮塔耶夫斯基方程的研究：准粒子与孤子》，*SciPost Physics*，12 (1): 023。arXiv:2106.15289。Bibcode: 2022ScPP...12...23K。doi: [10.21468/SciPostPhys.12.1.023](https://doi.org/10.21468/SciPostPhys.12.1.023)。ISSN: 2542-4653。S2CID: 235670023。
10. Choi, S.; Dunjko, V.; Zhang, Z. D.; Olshanii, M.（2015 年 9 月 10 日）.《从理想气体到 Tonks–Girardeau 区的调和阱中一维玻色气体的单极激发》，《物理评论快报》，115 (11): 115302。arXiv:1412.6855。Bibcode: 2015PhRvL.115k5302C。doi: [10.1103/PhysRevLett.115.115302](https://doi.org/10.1103/PhysRevLett.115.115302)。ISSN: 0031-9007。PMID: 26406838。S2CID: 2987641。
11. Peotta, Sebastiano; Ventra, Massimiliano Di（2014 年 1 月 24 日）.《超冷原子云碰撞中的量子激波与反转布居》，《物理评论 A》，89 (1): 013621。arXiv:1303.6916。Bibcode: 2014PhRvA..89a3621P。doi: [10.1103/PhysRevA.89.013621](https://doi.org/10.1103/PhysRevA.89.013621)。ISSN: 1050-2947。S2CID: 119290214。
12. N. M. Hugenholtz；D. Pines（1959）.《相互作用玻色体系的基态能与激发谱》，《物理评论》，116 (3): 489–506。Bibcode: 1959PhRv..116..489H。doi: [10.1103/PhysRev.116.489](https://doi.org/10.1103/PhysRev.116.489)。
13. Dalfovo, Franco；Giorgini, Stefano；Pitaevskii, Lev P.；Stringari, Sandro（1999 年 4 月 1 日）.《束缚气体中玻色–爱因斯坦凝聚的理论》，《现代物理评论》，71 (3): 463–512。arXiv\:cond-mat/9806038。Bibcode: 1999RvMP...71..463D。doi: [10.1103/RevModPhys.71.463](https://doi.org/10.1103/RevModPhys.71.463)。S2CID: 55787701。
14. P. Muruganandam 和 S. K. Adhikari（2009）.《完全各向异性势阱中时间依赖格罗斯–皮塔耶夫斯基方程的 Fortran 程序》，*Computer Physics Communications*，180 (3): 1888–1912。arXiv:0904.3131。Bibcode: 2009CoPhC.180.1888M。doi: [10.1016/j.cpc.2009.04.015](https://doi.org/10.1016/j.cpc.2009.04.015)。S2CID: 7403553。
15. P. Muruganandam 和 S. K. Adhikari（2003）.《通过伪谱法与有限差分法研究三维玻色–爱因斯坦凝聚体的动力学》，《物理学杂志 B》，36 (12): 2501–2514。arXiv\:cond-mat/0210177。Bibcode: 2003JPhB...36.2501M。doi: [10.1088/0953-4075/36/12/310](https://doi.org/10.1088/0953-4075/36/12/310)。S2CID: 250851068。
16. D. Vudragovic 等（2012）.《完全各向异性势阱中时间依赖格罗斯–皮塔耶夫斯基方程的 C 程序》，*Computer Physics Communications*，183 (9): 2021–2025。arXiv:1206.1361。Bibcode: 2012CoPhC.183.2021V。doi: [10.1016/j.cpc.2012.03.022](https://doi.org/10.1016/j.cpc.2012.03.022)。S2CID: 12031850。
17. L. E. Young-S. 等（2016）.《基于 OpenMP 的 Fortran 与 C 程序：用于完全各向异性势阱中时间依赖格罗斯–皮塔耶夫斯基方程的求解》，*Computer Physics Communications*，204 (9): 209–213。arXiv:1605.03958。Bibcode: 2016CoPhC.204..209Y。doi: [10.1016/j.cpc.2016.03.015](https://doi.org/10.1016/j.cpc.2016.03.015)。S2CID: 206999817。
18. R. Kishor Kumar 等（2015）.《完全各向异性势阱中时间依赖偶极格罗斯–皮塔耶夫斯基方程的 Fortran 与 C 程序》，*Computer Physics Communications*，195: 117–128。arXiv:1506.03283。Bibcode: 2015CoPhC.195..117K。doi: [10.1016/j.cpc.2015.03.024](https://doi.org/10.1016/j.cpc.2015.03.024)。S2CID: 18949735。
19. C. Raman、M. Köhl、R. Onofrio、D. S. Durfee、C. E. Kuklewicz、Z. Hadzibabic、W. Ketterle（1999）.《玻色–爱因斯坦凝聚气体中临界速度的实验证据》，*Physical Review Letters*，83 (13): 2502。arXiv\:cond-mat/9909109。Bibcode: 1999PhRvL..83.2502R。doi: [10.1103/PhysRevLett.83.2502](https://doi.org/10.1103/PhysRevLett.83.2502)。S2CID: 14070421。
20. A. Yu. Okulov（2008）.《光子的角动量与相位共轭》，《物理学杂志 B：原子、分子与光学物理》，41 (10): 101001。arXiv:0801.2675。Bibcode: 2008JPhB...41j1001O。doi: [10.1088/0953-4075/41/10/101001](https://doi.org/10.1088/0953-4075/41/10/101001)。S2CID: 13307937。
21. A. Yu. Okulov（2012）.《通过缓慢旋转的螺旋势捕获冷原子物质》，《物理快报 A》，376 (4): 650–655。arXiv:1005.4213。Bibcode: 2012PhLA..376..650O。doi: [10.1016/j.physleta.2011.11.033](https://doi.org/10.1016/j.physleta.2011.11.033)。S2CID: 119196009。
22. A. Yu. Okulov（2013）.《使用螺旋激光阱的超流旋转传感器》，《低温物理学杂志》，171 (3): 397–407。arXiv:1207.3537。Bibcode: 2013JLTP..171..397O。doi: [10.1007/s10909-012-0837-7](https://doi.org/10.1007/s10909-012-0837-7)。S2CID: 118601627。
23. A. Al. Rsheed、A. Lyras、V. E. Lembessis、O. M. Aldossary（2016）.《在螺旋光学势结构中导引原子》，《物理学杂志 B：原子、分子与光学物理》，49 (12): 125002。Bibcode: 2016JPhB...49l5002R。doi: [10.1088/0953-4075/49/12/125002](https://doi.org/10.1088/0953-4075/49/12/125002)。S2CID: 124660886。
24. M. J. Steel、M. K. Olsen、L. I. Plimak、P. D. Drummond、S. M. Tan、M. J. Collett、D. F. Walls、R. Graham（1998）.《束缚玻色–爱因斯坦凝聚体中的动态量子噪声》，《物理评论 A》，58 (6): 4824–4835。arXiv\:cond-mat/9807349。Bibcode: 1998PhRvA..58.4824S。doi: [10.1103/PhysRevA.58.4824](https://doi.org/10.1103/PhysRevA.58.4824)。S2CID: 43217083。
25. Zaremba, E；Nikuni, T；Griffin, A（1999）.《有限温度下束缚玻色气体的动力学》，《低温物理学杂志》，116 (3–4): 277–345。doi: [10.1023/A:1021846002995](https://doi.org/10.1023/A:1021846002995)。S2CID: 37753。
26. Stoof, H. T. C（1999）.《原子气体玻色–爱因斯坦凝聚过程中的相干与非相干动力学》，《低温物理学杂志》，114 (1–2): 11–108。doi: [10.1023/A:1021897703053](https://doi.org/10.1023/A:1021897703053)。S2CID: 16107086。
27. Davis, M. J；Morgan, S. A；Burnett, K（2001）.《有限温度下玻色场的数值模拟》，《物理评论快报》，87 (16): 160402。arXiv\:cond-mat/0011431。Bibcode: 2001PhRvL..87p0402D。doi: [10.1103/PhysRevLett.87.160402](https://doi.org/10.1103/PhysRevLett.87.160402)。PMID: 11690189。S2CID: 14195702。
28. Gardiner, C. W；Davis, M. J（2003）.《随机格罗斯–皮塔耶夫斯基方程：第二部分》，《物理学杂志 B：原子、分子与光学物理》，36 (23): 4731–4753。arXiv\:cond-mat/0308044。Bibcode: 2003JPhB...36.4731G。doi: [10.1088/0953-4075/36/23/010](https://doi.org/10.1088/0953-4075/36/23/010)。S2CID: 250874049。
29. Gardiner, S. A；Morgan, S. A（2007）.《玻色简并气体中凝聚态与非凝聚态动力学的最小自洽守数处理方法》，《物理评论 A》，75 (4): 043621。arXiv\:cond-mat/0610623。Bibcode: 2007PhRvA..75d3621G。doi: [10.1103/PhysRevA.75.043621](https://doi.org/10.1103/PhysRevA.75.043621)。S2CID: 119432906。
30. Proukakis, Nick P.；Jackson, Brian（2008）.《有限温度下的玻色–爱因斯坦凝聚模型》，《物理学杂志 B：原子、分子与光学物理》，41 (20): 203002。arXiv:0810.0210。doi: [10.1088/0953-4075/41/20/203002](https://doi.org/10.1088/0953-4075/41/20/203002)。ISSN: 0953-4075。S2CID: 118561792。访问日期：2022 年 2 月 14 日。
31. Blakie, P. B.；Bradley, A. S.；Davis, M. J.；Ballagh, R. J.；Gardiner, C. W.（2008 年 9 月 1 日）.《利用 c-场方法研究超冷玻色气体的动力学与统计力学》，《物理学进展》，57 (5): 363–455。arXiv:0809.1487。Bibcode: 2008AdPhy..57..363B。doi: [10.1080/00018730802564254](https://doi.org/10.1080/00018730802564254)。ISSN: 0001-8732。S2CID: 14999178。访问日期：2021 年 12 月 5 日。

4. 延伸阅读

• Pethick, C. J.；Smith, H.（2002）.《稀薄气体中的玻色–爱因斯坦凝聚》，剑桥：剑桥大学出版社。ISBN 978-0-521-66580-3。
• Pitaevskii, L. P.；Stringari, S.（2003）.《玻色–爱因斯坦凝聚》，牛津：克拉伦登出版社（。ISBN 978-0-19-850719-2。

5. 外部链接

• Trotter-Suzuki-MPI：一个基于 Trotter–Suzuki 分解的大规模模拟库，也可用于求解格罗斯–皮塔耶夫斯基方程。
• XMDS：一个谱方法偏微分方程库，可用于求解格罗斯–皮塔耶夫斯基方程。