动量（综述）

贡献者：待更新

　　本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章）

图 1：台球白球的动量在碰撞后传递给排列好的球。

　　在牛顿力学中，动量（复数：momenta 或 momentums；更具体地称为线动量或平动动量）是物体质量与速度的乘积。它是一个矢量量，具有大小和方向。如果物体的质量为 $m$ ，速度为 $v$ （也是矢量量），则该物体的动量 $p$ （来自拉丁语 pellere，意为 “推动”）表示为： $p = m v$ 在国际单位制（SI）中，动量的单位是千克米每秒（kg⋅m/s），在量纲上等同于牛顿秒。

　　牛顿的第二运动定律指出，物体动量的变化率等于作用在其上的合力。动量依赖于参考系，但在任何惯性系中都是守恒量，意味着如果一个封闭系统不受外力影响，其总动量保持不变。动量在狭义相对论中也守恒（采用修正的公式），并在电动力学、量子力学、量子场论和广义相对论中以修正的形式得到保留。它表达了时空的基本对称性之一：平移对称性。

　　经典力学的高级表述，如拉格朗日力学和哈密顿力学，允许选择包含对称性和约束的坐标系。在这些系统中，守恒量是广义动量，而一般情况下这不同于上述的动能动量。广义动量的概念被延续到量子力学中，在那里它成为作用于波函数的算符。动量算符和位置算符通过海森堡不确定性原理相联系。

　　在电磁场、流体动力学和可变形体等连续系统中，可以定义动量密度，即每单位体积的动量（体积特定的量）。动量守恒的连续体版本导致了诸如流体的纳维-斯托克斯方程或可变形固体或流体的柯西动量方程等方程。

1. 经典力学

　　动量是一个矢量量，具有大小和方向。由于动量具有方向性，因此可以用它来预测物体碰撞后的运动方向和速度。下面描述的是动量在一维中的基本性质。矢量方程与标量方程几乎相同（见多维情况）。

单个粒子

　　粒子的动量通常用字母 $p$ 表示，它是粒子质量（用字母 $m$ 表示）和速度（ $v$ ）的乘积：[1] $p = m v .$ 动量的单位是质量和速度单位的乘积。在国际单位制（SI）中，如果质量以千克（kg）为单位，速度以米每秒（m/s）为单位，那么动量的单位就是千克米每秒（kg⋅m/s）。在厘米-克-秒制（cgs）单位中，如果质量以克（g）为单位，速度以厘米每秒（cm/s）为单位，那么动量的单位就是克厘米每秒（g⋅cm/s）。

　　作为一个矢量，动量具有大小和方向。例如，一个质量为 1 kg 的模型飞机，以 1 m/s 的速度正北方向平稳飞行，其相对于地面的动量为 1 kg⋅m/s，方向为正北。

多粒子系统

　　一个粒子系统的动量是它们各自动量的矢量和。如果两个粒子分别有质量 $m_{1}$ 和 $m_{2}$ ，速度为 $v_{1}$ 和 $v_{2}$ ，则总动量为 $p = p_{1} + p_{2} = m_{1} v_{1} + m_{2} v_{2} .$ 对于超过两个粒子的系统，可以更一般地表示为： $p = \sum_{i} m_{i} v_{i} .$ 一个粒子系统有一个质心，这个点由它们位置的加权和确定： $r_{cm} = \frac{m_{1} r_{1} + m_{2} r_{2} + \dots}{m_{1} + m_{2} + \dots} = \frac{\sum_{i} m_{i} r_{i}}{\sum_{i} m_{i}} .$ 如果一个或多个粒子在运动，那么系统的质心一般也会运动（除非系统绕质心纯粹旋转）。如果粒子的总质量为 $m$ ，且质心的速度为 $v_{cm}$ ，那么系统的动量为： $p = m v_{cm} .$ 这被称为欧拉第一定律。[2][3]

与力的关系

　　如果作用在粒子上的净力 $F$ 是恒定的，并且作用时间间隔为 $Δ t$ ，则粒子的动量会改变一个量： $Δ p = F Δ t .$ 在微分形式中，这是牛顿第二定律；粒子动量的变化率等于作用在其上的瞬时力 $F$ ，[1] $F = \frac{d p}{d t} .$ 如果粒子所受的净力是时间的函数 $F (t)$ ，那么在时间 $t_{1}$ 和 $t_{2}$ 之间的动量变化（或冲量 $J$ ）为： $Δ p = J = \int_{t_{1}}^{t_{2}} F (t) d t .$ 冲量的单位是导出单位牛顿秒（1 N⋅s = 1 kg⋅m/s）或达因秒（1 dyne⋅s = 1 g⋅cm/s）。

　　在假设质量 $m$ 恒定的情况下，可以写成： $F = \frac{d (m v)}{d t} = m \frac{d v}{d t} = m a,$ 因此，净力等于粒子的质量乘以其加速度。[1]

　　示例：一个质量为 1 kg 的模型飞机从静止加速到正北方向的速度 6 m/s，所需时间为 2 秒。产生这种加速度所需的净力为 3 牛顿（正北方向）。动量的变化为 6 kg⋅m/s（正北方向）。动量的变化率为 3 (kg⋅m/s)/s（正北方向），其数值上等于 3 牛顿。

动量守恒

　　在封闭系统（即不与周围环境交换任何物质且不受外力作用的系统）中，总动量保持不变。这一事实被称为动量守恒定律，由牛顿运动定律隐含推导出来。[4][5] 例如，假设两个粒子相互作用。根据第三定律，它们之间的作用力大小相等，但方向相反。如果粒子编号为 1 和 2，第二定律表示 $F_{1} = \frac{d p_{1}}{d t}$ 和 $F_{2} = \frac{d p_{2}}{d t}$ 。因此， $\frac{d p_{1}}{d t} = - \frac{d p_{2}}{d t},$ 负号表示力的方向相反。同样地， $\frac{d}{d t} (p_{1} + p_{2}) = 0.$ 如果粒子在相互作用之前的速度分别为 $v_{A 1}$ 和 $v_{B 1}$ ，而相互作用后的速度分别为 $v_{A 2}$ 和 $v_{B 2}$ ，那么 $m_{A} v_{A 1} + m_{B} v_{B 1} = m_{A} v_{A 2} + m_{B} v_{B 2} .$ 无论粒子之间的作用力多么复杂，该定律始终成立。同样，如果存在多个粒子，每对粒子之间交换的动量总和为零，因此动量的总变化为零。多个相互作用粒子的总动量守恒可以表示为：[4] $m_{A} v_{A} + m_{B} v_{B} + m_{C} v_{C} + \dots = 常量 .$ 该守恒定律适用于所有相互作用，包括碰撞（弹性和非弹性）以及由爆炸力引起的分离。[4] 它也可以推广到牛顿定律不适用的情况，例如相对论和电动力学中的情况。[6]

对参考系的依赖性

　　动量是一个可测量的量，且测量结果取决于参考系。例如，如果一架质量为 1000 kg 的飞机以 50 m/s 的速度在空中飞行，其动量可以计算为 50,000 kg·m/s。如果飞机迎着 5 m/s 的逆风飞行，那么相对于地球表面的速度只有 45 m/s，其动量计算为 45,000 kg·m/s。这两种计算都同样正确。在两个参考系中，动量的任何变化都与相关的物理定律一致。

　　假设 $x$ 是一个惯性参考系中的位置。从另一个相对于第一个参考系以恒定速度 $u$ 移动的参考系的角度来看，位置（用加撇的坐标表示）随时间的变化为： $x^{'} = x - u t .$ 这称为伽利略变换。

　　如果一个粒子在第一个参考系中的速度为 $\frac{d x}{d t} = v$ ，那么在第二个参考系中，它的速度为： $v^{'} = \frac{d x^{'}}{d t} = v - u .$ 由于 $u$ 不变，第二个参考系也是一个惯性参考系，且加速度相同： $a^{'} = \frac{d v^{'}}{d t} = a .$ 因此，在这两个参考系中动量都是守恒的。此外，只要力的形式相同，牛顿第二定律在这两个参考系中也是不变的。像牛顿引力这样仅依赖于物体之间的标量距离的力满足这一标准。这种参考系的独立性称为牛顿相对性或伽利略不变性。[7]

　　改变参考系通常可以简化运动的计算。例如，在两个粒子的碰撞中，可以选择一个参考系，使其中一个粒子开始时处于静止状态。另一个常用的参考系是质心参考系——即随质心一起运动的参考系。在该参考系中，总动量为零。

碰撞的应用

　　如果两个具有已知动量的粒子碰撞并合并在一起，那么可以使用动量守恒定律来确定合并后物体的动量。如果碰撞结果是两个粒子分离，动量守恒定律则不足以确定每个粒子的动量。如果碰撞后已知其中一个粒子的动量，则该定律可以用来确定另一个粒子的动量。或者，如果碰撞后的总动能已知，也可以利用该定律来确定每个粒子碰撞后的动量。[8] 动能通常不会守恒。如果动能守恒，这种碰撞称为弹性碰撞；如果不守恒，则称为非弹性碰撞。

　　 弹性碰撞

图 2

　　弹性碰撞是指没有动能转化为热能或其他形式能量的碰撞。完美弹性碰撞可能发生在物体不接触的情况下，例如在原子或核散射中，电排斥力使物体分开。卫星绕行行星的弹弓效应也可视为完美的弹性碰撞。两个台球的碰撞是一个几乎完全弹性碰撞的例子，由于它们的高刚性，但当物体接触时总会有一些能量损耗。[9]

　　两个物体之间的正面弹性碰撞可以通过沿穿过物体的直线的一维速度来表示。如果在碰撞前速度为 $v_{A 1}$ 和 $v_{B 1}$ ，而在碰撞后速度为 $v_{A 2}$ 和 $v_{B 2}$ ，则表达动量和动能守恒的方程为： $m_{A} v_{A 1} + m_{B} v_{B 1} = m_{A} v_{A 2} + m_{B} v_{B 2}$ $\frac{1}{2} m_{A} v_{A 1}^{2} + \frac{1}{2} m_{B} v_{B 1}^{2} = \frac{1}{2} m_{A} v_{A 2}^{2} + \frac{1}{2} m_{B} v_{B 2}^{2}$ 通过改变参考系可以简化碰撞分析。例如，假设有两个质量相等的物体 $m$ ，一个静止，另一个以速度 $v$ 接近静止的物体。质心的移动速度为 $\frac{v}{2}$ ，两个物体都以速度 $\frac{v}{2}$ 向质心移动。由于对称性，碰撞后两者都必须以相同的速度远离质心。将质心的速度加到两者上，我们发现原本移动的物体现在停止，而另一物体以速度 $v$ 远离。两个物体交换了它们的速度。无论物体的初始速度如何，切换到质心参考系都会得出相同的结论。因此，最终速度为： $v_{A 2} = v_{B 1}$ $v_{B 2} = v_{A 1}$ 一般情况下，当已知初速度时，最终速度为：[10] $v_{A 2} = (\frac{m_{A} - m_{B}}{m_{A} + m_{B}}) v_{A 1} + (\frac{2 m_{B}}{m_{A} + m_{B}}) v_{B 1}$ $v_{B 2} = (\frac{m_{B} - m_{A}}{m_{A} + m_{B}}) v_{B 1} + (\frac{2 m_{A}}{m_{A} + m_{B}}) v_{A 1}$ 如果一个物体的质量远大于另一个物体，那么它的速度在碰撞后几乎不会受到影响，而另一个物体的速度会发生显著变化。

　　 非弹性碰撞
在非弹性碰撞中，一部分碰撞物体的动能被转化为其他形式的能量（例如热能或声能）。例如，交通事故中，[11]动能的损失表现为车辆的损坏；电子将部分能量传递给原子（如在弗兰克-赫兹实验中）；[12]以及在粒子加速器中，动能转化为以新粒子形式出现的质量。

　　在完全非弹性碰撞（如虫子撞上挡风玻璃）中，碰撞后两个物体具有相同的运动状态。一次正面非弹性碰撞可以通过一维速度来表示，即沿通过物体的直线。如果在碰撞前速度分别为 $v_{A 1}$ 和 $v_{B 1}$ ，那么在完全非弹性碰撞中，两个物体将以速度 $v_{2}$ 一起运动。动量守恒方程为： $m_{A} v_{A 1} + m_{B} v_{B 1} = (m_{A} + m_{B}) v_{2} .$ 如果一个物体最初是静止的（例如 $v_{B 1} = 0$ ），动量守恒方程为： $m_{A} v_{A 1} = (m_{A} + m_{B}) v_{2},$ 所以 $v_{2} = \frac{m_{A}}{m_{A} + m_{B}} v_{A 1} .$ 在另一种情况下，如果参照系以最终速度 $v_{2}$ 移动，使得碰撞后的合并速度为零（即 $v_{2} = 0$ ），则完全非弹性碰撞会使物体停下，且 100% 的动能被转化为其他形式的能量。在这种情况下，物体的初始速度将不为零，或物体质量为零。

　　碰撞的非弹性程度可以通过恢复系数 $C_{R}$ 来衡量，该系数定义为分离的相对速度与接近的相对速度的比值。在将此度量应用于球从固体表面弹起时，可以通过以下公式轻松测量：[13] $C_{R} = \sqrt{\frac{弹跳高度}{下落高度}} .$ 动量和能量方程也适用于起初在一起然后分开的物体的运动。例如，爆炸是化学、机械或核形式的潜在能量通过连锁反应转化为动能、声能和电磁辐射的结果。火箭也利用动量守恒原理：推进剂被向外喷出，获得动量，同时给火箭施加了等量反向的动量。[14]

多维度

图 3：二维弹性碰撞。图像中没有垂直方向的运动，因此仅需两个分量来表示速度和动量。两个蓝色矢量表示碰撞后的速度，矢量相加后得到初始的（红色）速度。

　　真实的运动既有方向也有速度，必须用矢量表示。在具有 $x, y, z$ 轴的坐标系中，速度在 $x$ 方向上的分量为 $v_{x}, y$ 方向上的分量为 $v_{y}, z$ 方向上的分量为 $v_{z}$ 。矢量用粗体符号表示：[15] $v = (v_{x}, v_{y}, v_{z})$ 同样，动量也是一个矢量量，用粗体符号表示： $p = (p_{x}, p_{y}, p_{z})$ 在之前的部分中，方程在矢量形式下也适用，只需将标量 $p$ 和 $v$ 替换为矢量 $p$ 和 $v$ 。每个矢量方程代表三个标量方程。例如， $p = m v$ 表示三个方程：[15] $\begin{aligned} p_{x} & = m v_{x} \\ p_{y} & = m v_{y} \\ p_{z} & = m v_{z} \end{aligned}$ 动能方程是上述替换规则的例外。方程仍然是一维的，但每个标量代表矢量的大小，例如， $v^{2} = v_{x}^{2} + v_{y}^{2} + v_{z}^{2}$ 每个矢量方程代表三个标量方程。通常可以选择坐标，使得只需要两个分量，如图所示。每个分量可以单独求出，结果结合起来得出矢量结果。[15]

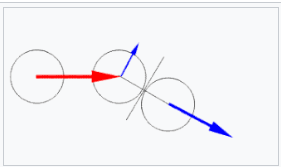
　　通过使用质心参考系的简单构造，可以表明，如果一个静止的弹性球体被一个移动的球体撞击，碰撞后两个球体会以直角方向分开运动（如图所示）。[16]

变质量物体

　　动量的概念在解释变质量物体（如喷射燃料的火箭或吸积气体的恒星）的行为时起着基础性作用。在分析此类物体时，将物体的质量视为随时间变化的函数： $m (t)$ 。因此，物体在时间 $t$ 的动量为 $p (t) = m (t) v (t)$ 。此时，可能会尝试通过牛顿第二定律来说明作用在物体上的外力 $F$ 与其动量 $p (t)$ 的关系为 $F = \frac{d p}{d t}$ ，但这是错误的，类似地，应用积的求导法则得出的以下表达式也是错误的：[17] $F = m (t) \frac{d v}{d t} + v (t) \frac{d m}{d t} （错误）$ 这个方程无法正确描述变质量物体的运动。正确的方程为 $F = m (t) \frac{d v}{d t} - u \frac{d m}{d t}$ 其中， $u$ 是在物体参考系中观测到的喷出或吸积物质的速度，这与 $v$ （即在惯性参考系中观测到的物体自身的速度）不同。

　　这个方程的推导过程中，必须同时追踪物体的动量和喷出/吸积物质（ $d m$ ）的动量。当将物体和物质 $d m$ 一起考虑时，它们构成了一个总动量守恒的封闭系统。 $P (t + d t) = (m - d m) (v + d v) + d m (v - u) = m v + m d v - u d m = P (t) + m d v - u d m$ 这就得到了总动量守恒的公式。

2. 广义动量

　　牛顿定律在许多类型的运动中应用起来较为困难，因为这些运动受到约束的限制。例如，算盘上的珠子被限制在导线沿线上移动，摆锤的摆球被限制在固定的枢轴距离处摆动。许多此类约束可以通过将普通的笛卡尔坐标转换为一组可能数量较少的广义坐标来引入。[18] 为了在广义坐标下解决力学问题，已开发出精细的数学方法。这些方法引入了广义动量（也称为正则动量或共轭动量），它扩展了线性动量和角动量的概念。为了与广义动量区分，质量和速度的乘积也称为机械动量、动能动量或运动学动量。[6][19][20] 下面介绍了两种主要方法。

拉格朗日力学

　　在拉格朗日力学中，拉格朗日量被定义为动能 $T$ 和势能 $V$ 的差值： $L = T - V .$ 如果广义坐标表示为向量 $q = (q_{1}, q_{2}, \dots, q_{N})$ ，时间的微分表示为变量上方的点，那么运动方程（称为拉格朗日方程或欧拉-拉格朗日方程）是一组 $N$ 个方程：[21] $\frac{d}{d t} (\frac{\partial L}{\partial {\dot{q}}_{j}}) - \frac{\partial L}{\partial q_{j}} = 0.$ 如果坐标 $q_{i}$ 不是笛卡尔坐标，则相关的广义动量分量 $p_{i}$ 不一定具有线性动量的维度。即使 $q_{i}$ 是笛卡尔坐标，如果势能依赖于速度， $p_{i}$ 也不等于机械动量。[6] 一些资料用符号 $Π$ 表示运动动量。[22]

　　在此数学框架中，广义动量与广义坐标相关联。其分量定义为 $p_{j} = \frac{\partial L}{\partial {\dot{q}}_{j}} .$ 每个分量 $p_{j}$ 被称为坐标 $q_{j}$ 的共轭动量。

　　如果某个坐标 $q_{i}$ 未出现在拉格朗日量中（尽管其时间导数可能会出现），则 $p_{j}$ 是常数。这是动量守恒的广义形式。[6]

　　即使广义坐标只是普通的空间坐标，共轭动量也不一定是普通的动量坐标。一个例子可以在电磁学部分找到。

哈密顿力学

　　在哈密顿力学中，拉格朗日量（一个广义坐标和其导数的函数）被替换为哈密顿量，该量是广义坐标和动量的函数。哈密顿量定义为 $H (q, p, t) = p \cdot \dot{q} - L (q, \dot{q}, t),$ 其中动量通过如上所述对拉格朗日量求导获得。哈密顿运动方程为：[23] ${\dot{q}}_{i} = \frac{\partial H}{\partial p_{i}}, - {\dot{p}}_{i} = \frac{\partial H}{\partial q_{i}}, - \frac{\partial L}{\partial t} = \frac{d H}{d t} .$ 同样地，在哈密顿力学中，如果广义坐标未出现在哈密顿量中，则其共轭动量分量是守恒的。[24]

对称性与守恒

　　动量守恒是空间均匀性（平移对称性）的数学结果（空间中的位置是动量的共轭量）。也就是说，动量守恒源于物理定律不依赖于位置；这是诺特定理的一个特殊情况。[25] 对于不具有这种对称性的系统，可能无法定义动量守恒。动量守恒不适用的示例包括广义相对论中的弯曲时空[26]或凝聚态物理中的时间晶体。[27][28][29][30]

3. 动量密度

在可变形体和流体中的应用

　　 连续体中的守恒

图 4：物体的运动

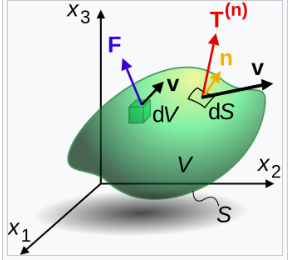
　　在流体力学和固体力学等领域中，跟踪单个原子或分子的运动是不现实的。因此，材料必须通过一个连续体来近似描述，其中在每一点上存在一个粒子或流体小体，分配给它的是附近小区域中原子的属性的平均值。特别是，它具有密度 $ρ$ 和速度 $v$ ，这些属性依赖于时间 $t$ 和位置 $r$ 。每单位体积的动量是 $ρ v$ 。[31]

　　考虑一个处于静水平衡的水柱，所有的力都处于平衡状态，水体静止不动。在任何给定的水滴上，有两种力平衡。第一种是重力，直接作用在内部的每个原子和分子上。每单位体积的重力为 $ρ g$ ，其中 $g$ 是重力加速度。第二种力是由周围水体施加在其表面上的力的总和。下方的力比上方的力大，恰好抵消了重力。每单位面积的法向力为压力 $p$ 。在水滴内部，平均每单位体积的力为压力的梯度，因此力平衡方程为：[32] $- \nabla p + ρ g = 0$ 如果这些力不平衡，水滴将会加速。这种加速度不仅仅是偏导数 $\frac{\partial v}{\partial t}$ ，因为给定体积内的流体会随时间变化。因此，需要使用物质导数：[33] $\frac{D}{D t} \equiv \frac{\partial}{\partial t} + v \cdot \nabla$ 应用于任何物理量时，物质导数包括了在一个点上的变化率以及由于随流动而引起的变化。每单位体积的动量变化率等于 $ρ \frac{D v}{D t}$ ，这等于水滴上的净力。

　　改变水滴动量的力包括压力梯度和重力。此外，表面力可以使水滴发生变形。在最简单的情况下，剪切应力 $τ$ 由平行于水滴表面的力施加，与变形速率或应变速率成正比。如果流体的速度在某个方向上存在梯度，因为流体在一侧比另一侧运动得更快，则产生这种剪切应力。若速度在 $x$ 方向上随着 $z$ 变化，则法向 $z$ 方向上的单位面积内在 $x$ 方向上的切向力为： $σ_{z x} = - μ \frac{\partial v_{x}}{\partial z}$ 其中 $μ$ 为粘度。这也是 $x$ 动量通过表面的流量或每单位面积的流量。[34]

　　考虑粘度的影响，牛顿流体不可压缩流动的动量平衡方程为： $ρ \frac{D v}{D t} = - \nabla p + μ \nabla^{2} v + ρ g$ 这被称为纳维-斯托克斯方程。[35]

　　动量平衡方程可以扩展到更广泛的材料，包括固体。对于具有方向 $i$ 的法向和方向 $j$ 的力的每个表面，都存在一个应力分量 $σ_{i j}$ 。九个分量组成了柯西应力张量 $σ$ ，它包含了压力和剪切。局部动量守恒由柯西动量方程表示： $ρ \frac{D v}{D t} = \nabla \cdot σ + f$ 其中 $f$ 是体力。[36]

　　柯西动量方程广泛适用于固体和液体的变形。应力和应变速率之间的关系取决于材料的特性。

　　声波
在介质中的扰动会引发震荡或波动，从其源点向外传播。在流体中，小的压力变化 $p$ 通常可以用声波方程描述： $\frac{\partial^{2} p}{\partial t^{2}} = c^{2} \nabla^{2} p,$ 其中 $c$ 是声速。在固体中，可以得到类似的方程，用于描述压力波（P 波）和剪切波（S 波）的传播。[37]

　　动量分量 $ρ v_{j}$ 通过速度 $v_{i}$ 的通量或单位面积的传输等于 $ρ v_{i} v_{j}$ 。在导出上述声学方程的线性近似下，此通量的时间平均值为零。然而，非线性效应可能会引起非零的平均值。[38] 即使波本身没有平均动量，动量通量仍然可能发生。[39]

在电磁学中

　　 场中的粒子
在麦克斯韦方程中，粒子之间的力是由电场和磁场介导的。带电粒子 $q$ 在电场 $E$ 和磁场 $B$ 作用下受到的电磁力（洛伦兹力）为： $F = q (E + v \times B)$ （在 SI 单位中）。[40]:2 它具有电势 $ϕ (r, t)$ 和磁矢势 $A (r, t)$ 。在非相对论情况下，其广义动量为 $P = m v + q A$ 而在相对论力学中，这变为 $P = γ m v + q A$ 其中 $V = q A$ 有时称为势动量。[41][42][43] 它是由于粒子与电磁场相互作用而产生的动量。该名称是与势能 $U = q ϕ$ 的类比，后者是粒子与电磁场相互作用的能量。这些量形成了一个四维矢量，因此这种类比是一致的；此外，势动量的概念在解释所谓的电磁场的 “隐含动量” 中具有重要作用。[44]

　　 动量守恒
在牛顿力学中，动量守恒定律可以从作用力和反作用力法则推导出来，该法则表明每一个力都有一个相等且相反的力。在某些情况下，移动的带电粒子可以在非相反方向上相互施加力。[45] 尽管如此，粒子与电磁场的总动量仍然是守恒的。

　　真空
洛伦兹力会给粒子带来动量，因此根据牛顿第二定律，粒子必须将动量传递给电磁场。[46]

　　在真空中，每单位体积的动量为 $g = \frac{1}{μ_{0} c^{2}} E \times B,$ 其中， $μ_{0}$ 是真空磁导率， $c$ 是光速。动量密度与波印廷矢量 $S$ 成正比，后者表示每单位面积的能量传输速率方向：[46][47] $g = \frac{S}{c^{2}} .$ 为了在区域 $Q$ 内的体积 $V$ 上实现动量守恒，洛伦兹力对物质动量的改变必须与电磁场动量的变化和平衡的动量流出相匹配。如果 $P_{mech}$ 是区域 $Q$ 内所有粒子的动量，并且粒子被视为连续体，那么根据牛顿第二定律 $\frac{d P_{mech}}{d t} = ∭_{Q} (ρ E + J \times B) d V .$ 电磁场的动量为 $P_{field} = \frac{1}{μ_{0} c^{2}} ∭_{Q} E \times B d V,$ 每个动量分量 $i$ 的守恒方程为 $\frac{d}{d t} {(P_{mech} + P_{field})}_{i} = \iint_{σ} (\sum_{j} T_{i j} n_{j}) d Σ .$ 右侧的项是在表面区域 $Σ$ 上的积分，表示动量进入和离开体积的流动， $n_{j}$ 是表面法向量 $S$ 的分量。量 $T_{i j}$ 称为麦克斯韦应力张量，定义为[46] $T_{i j} \equiv ϵ_{0} (E_{i} E_{j} - \frac{1}{2} δ_{i j} E^{2}) + \frac{1}{μ_{0}} (B_{i} B_{j} - \frac{1}{2} δ_{i j} B^{2}) .$

　　介质
以上结果适用于真空中的微观麦克斯韦方程（或介质中非常小尺度的电磁力）。在介质中定义动量密度更为困难，因为电磁和机械的划分是任意的。电磁动量密度的定义被修改为： $g = \frac{1}{c^{2}} E \times H = \frac{S}{c^{2}},$ 其中，H 场 $H$ 与 B 场和磁化 $M$ 的关系为： $B = μ_{0} (H + M) .$ 电磁应力张量取决于介质的特性。[46]

4. 非经典力学

量子力学

　　进一步信息：动量算符在量子力学中，动量被定义为一个作用于波函数的自伴算符。海森堡不确定性原理规定了在同一时间内对一个可观测系统的动量和位置的测量精度的限制。在量子力学中，位置和动量是共轭变量。

　　对于以位置为基描述的单粒子，动量算符可以写为： $p = \frac{ℏ}{i} \nabla = - i ℏ \nabla,$ 其中 $\nabla$ 是梯度算符， $ℏ$ 是约化普朗克常数， $i$ 是虚数单位。这是动量算符的一种常见形式，但在其他基中，动量算符可能有不同的形式。例如，在动量空间中，动量算符由以下本征值方程表示： $p ψ (p) = p ψ (p),$ 其中，算符 $p$ 作用于波本征函数 $ψ (p)$ 时，得到的是该波函数乘以本征值 $p$ ，类似于位置算符作用于波函数 $ψ (x)$ 时得到波函数乘以本征值 $x$ 的情况。

　　对于有质量和无质量物体，相对论动量与相位常数 $β$ 的关系为：[48] $p = ℏ β .$ 电磁辐射（包括可见光、紫外光和无线电波）由光子携带。尽管光子（光的粒子性）没有质量，但它们仍然携带动量。这一特性应用于如太阳帆等技术。计算介质中的光动量存在一定的争议（参见亚伯拉罕–明科夫斯基争论）。[49][50]

相对论动量

　　 洛伦兹不变性
牛顿物理学假设绝对时间和空间独立于任何观察者存在，这引发了伽利略不变性，也意味着光速在不同参考系之间可能有所不同。然而，这与实际观测结果相悖。在狭义相对论中，爱因斯坦保留了运动方程不依赖于参考系的假设，同时假设光速 $c$ 是不变的。因此，在两个参考系中的位置和时间是通过洛伦兹变换而非伽利略变换关联的。[51]

　　例如，考虑一个参考系相对于另一个参考系以 $v$ 速度沿 $x$ 方向移动。伽利略变换将移动的参考系坐标表示为： $\begin{aligned} t^{'} & = t \\ x^{'} & = x - v t \end{aligned}$ 而洛伦兹变换则为[52]： $\begin{aligned} t^{'} & = γ (t - \frac{v x}{c^{2}}) \\ x^{'} & = γ (x - v t) \end{aligned}$ 其中， $γ$ 是洛伦兹因子： $γ = \frac{1}{\sqrt{1 - v^{2} / c^{2}}} .$ 牛顿第二定律在质量固定的情况下不具有洛伦兹不变性。然而，如果将物体的惯性质量 $m$ 设为速度的函数，则可以实现不变性： $m = γ m_{0};$ 其中， $m_{0}$ 是物体的不变质量。[53]

　　修改后的动量为： $p = γ m_{0} v,$ 满足牛顿第二定律： $F = \frac{d p}{d t} .$ 在经典力学的范围内，相对论动量接近于牛顿动量：当速度较低时， $γ m_{0} v$ 近似等于 $m_{0} v$ ，即牛顿动量表达式。

　　 四矢量表述
在狭义相对论理论中，物理量以四矢量形式表示，时间作为第四个坐标，加入三个空间坐标。这些矢量通常用大写字母表示，例如位置矢量 $R$ 。四动量的表达式取决于坐标的表示方式。时间可以用正常单位表示，也可以乘以光速 $c$ ，使四矢量的所有分量都具有长度的量纲。如果采用后一种缩放方式，那么定义的固有时间间隔 $τ$ 为：[54] $c^{2} d τ^{2} = c^{2} d t^{2} - d x^{2} - d y^{2} - d z^{2},$ 该间隔在洛伦兹变换下保持不变（此表达式及以下内容采用了 $(+ - - -)$ 的度量符号，不同作者使用不同的约定）。在数学上，可以通过以下两种方式保证这种不变性：将四矢量视为欧几里得矢量并将时间乘以 $\sqrt{- 1}$ ；或保持时间为实数并将矢量嵌入到闵可夫斯基空间中。[55] 在闵可夫斯基空间中，两个四矢量 $U = (U_{0}, U_{1}, U_{2}, U_{3})$ 和 $V = (V_{0}, V_{1}, V_{2}, V_{3})$ 的标量积定义为 $U \cdot V = U_{0} V_{0} - U_{1} V_{1} - U_{2} V_{2} - U_{3} V_{3} .$ 在所有坐标系中，相对论性（逆变）四速度定义为 $U \equiv \frac{d R}{d τ} = γ \frac{d R}{d t},$ 而（逆变）四动量为 $P = m_{0} U,$ 其中 $m_{0}$ 是不变质量。如果 $R = (c t, x, y, z)$ （在闵可夫斯基空间中），则 $P = γ m_{0} (c, v) = (m c, p) .$ 利用爱因斯坦的质能等价关系 $E = m c^{2}$ ，可以改写为 $P = (\frac{E}{c}, p) .$ 因此，四动量守恒是洛伦兹不变的，并暗含了质量和能量的守恒。

　　四动量的模等于 $m_{0} c$ ： $‖ P ‖^{2} = P \cdot P = γ^{2} m_{0}^{2} (c^{2} - v^{2}) = (m_{0} c)^{2},$ 并且在所有参考系中是不变的。

　　相对论能量-动量关系也适用于无质量粒子（如光子）；设 $m_{0} = 0$ ，则有 $E = p c .$ 在相对论性的 “台球游戏” 中，如果一个静止粒子被一个运动的粒子弹性碰撞后，两者形成的路径将呈锐角。这与非相对论性情况不同，后者中它们会呈直角运动。[56]

　　平面波的四动量可以与波的四矢量相关联：[57] $P = (\frac{E}{c}, \vec{p}) = ℏ K = ℏ (\frac{ω}{c}, \vec{k})$ 对于粒子，时间分量之间的关系 $E = ℏ ω$ 是普朗克-爱因斯坦关系，而空间分量之间的关系 $p = ℏ k$ 描述了德布罗意物质波。

5. 概念的历史

动力

　　 约翰·菲洛波努斯
大约在公元 530 年，约翰·菲洛波努斯在《物理学评注》中提出了动量的概念，这是他对亚里士多德《物理学》的一种评论。亚里士多德认为，任何正在运动的物体都必须由某种东西持续推动。例如，一个被抛出的球必须依靠空气的流动来维持运动。菲洛波努斯指出亚里士多德这一说法的荒谬之处，即一个物体的运动居然是由阻碍它前进的同一空气所推动。他提出，物体在被抛出时获得了一种动力（impetus）。[58]

　　 伊本·西那

图 5：伊本·西那 (980–1037)

　　在 1020 年，伊本·西那（拉丁化名字为阿维森纳）阅读了斐洛波努斯的著作，并在《治愈之书》中发表了他自己的运动理论。他同意投掷物会被投掷者赋予一种动力；但与斐洛波努斯不同的是，斐洛波努斯认为这种动力即便在真空中也会逐渐衰减，而伊本·西那认为这种动力是持久的，需要外部力量（如空气阻力）来消散它。[59][60][61]

　　 彼得·奥利维，尚·布里丹
在 13 世纪和 14 世纪，彼得·奥利维和尚·布里丹研究并改进了斐洛波诺斯的工作，也可能参考了伊本·西那的理论。[61] 大约在 1350 年，布里丹被任命为巴黎大学校长，他提出了冲力与物体的重量和速度成正比。此外，布里丹的理论与他的前辈不同之处在于，他并不认为冲力会自我消散，而是认为物体会因为空气阻力和重力（可能会抵消其冲力）而停止运动。[62][63]

运动量

　　 勒内·笛卡尔
在 1644 年出版的《哲学原理》（*Principia Philosophiae*）中，法国哲学家勒内·笛卡尔将 “运动量”（拉丁语：*quantitas motus*）定义为大小与速度的乘积，[64]并声称宇宙中的总运动量是守恒的。[64][65]

　　如果 x 的大小是 y 的两倍，而速度是 y 的一半，那么两者的运动量相同。

　　 [上帝]创造了物质及其运动...仅仅是通过任由事物按其自身规律运转，他就保持了同样的运动量……就像他在最初放置的那样。

图 6：勒内·笛卡尔（1596 年－1650 年）

　　这不应被理解为现代动量守恒定律的陈述，因为笛卡尔并没有将质量区分于重量和大小的概念。（质量的概念区别于重量，是牛顿在 1686 年引入的。）[66] 更重要的是，笛卡尔认为是速度而非速度矢量被守恒。因此，对于笛卡尔而言，如果一个运动的物体弹离一个表面，改变了方向但不改变速度，其运动量不会发生变化。[67][68][69]

　　伽利略在其 1638 年出版的《两门新科学》中，也使用意大利词*impeto*来描述类似于笛卡尔的运动量概念。

　　 克里斯蒂安·惠更斯

图 7：克里斯蒂安·惠更斯 (1629–1695)

　　在 1600 年代，克里斯蒂安·惠更斯早期就得出结论，笛卡尔关于两个物体弹性碰撞的定律一定是错误的，并且他制定了正确的定律。[70] 他认识到问题的伽利略不变性，这是一个重要的进展。[71] 然而，他的观点花了多年才得以传播。1661 年，他在伦敦亲自将这些理论传递给威廉·布朗克和克里斯托弗·雷恩。[72] 在 1666 年第二次英荷战争期间，斯宾诺莎在写给亨利·奥登堡的信中提到这些理论时言辞谨慎。[73] 实际上，惠更斯早在 1652-1656 年间就在手稿《物体碰撞运动》中研究出了这些结论。战争于 1667 年结束，惠更斯在 1668 年向皇家学会宣布了他的结果，并于 1669 年在《学者杂志》上发表了这些发现。[74]

动量

　　 约翰·沃利斯
1670 年，约翰·沃利斯在《力学即运动的几何学论》中提出了动量守恒定律：“物体的初始状态，无论是静止还是运动，将会持续不变”，以及 “如果力大于阻力，则会产生运动”。沃利斯使用 “动量” 来表示 “运动量”，用 “力” 来表示 “力的大小”。

　　 戈特弗里德·莱布尼茨
1686 年，戈特弗里德·威廉·莱布尼茨在《形而上学论》中提出了反对笛卡尔 “运动量守恒” 构想的论点，通过不同大小的物块从不同高度落下的例子。他指出，力是守恒的，但被解释为物体大小与速度之积的 “运动量” 并非守恒。

　　 艾萨克·牛顿

图 8：艾萨克·牛顿 (1642–1727)

　　 1687 年，艾萨克·牛顿在《自然哲学的数学原理》（*Philosophiæ Naturalis Principia Mathematica*）中，和沃利斯一样，表现出类似的措辞探索来描述数学上的动量。在他的定义 II 中，将 “运动量”（*quantitas motus*）定义为 “源于速度和物质量的共同作用”，明确了它是动量。[77]因此，当他在第二定律中提到 “运动的变化”（*mutatio motus*）与施加的力成正比时，通常被理解为指动量的变化，而不是指单纯的运动。[78]

　　 约翰·詹宁斯
约翰·詹宁斯（*John Jennings*）在 1721 年出版了《杂集》（*Miscellanea*），其中动量在其当前的数学意义上首次得到验证，比牛顿《自然哲学的数学原理》最终版早了五年。动量 *M* 或 “运动量” 被定义为学生的 “矩形”，即 *Q* 和 *V* 的乘积，其中 *Q* 表示 “物质量”，*V* 表示 “速度”（即距离/时间）。

　　 1728 年，《百科全书》（*Cyclopedia*）中写道：

　　任何物体的动量、冲力或运动量，是其速度（或在给定时间内运动的距离，见‘运动’）与其质量的乘积。

6. 参见

角动量
晶体动量
伽利略炮
动量压缩
动量转移
牛顿摆
位置和动量空间

7. 参考文献

　　
1. 《费曼物理学讲义》卷 I 第 9 章：牛顿动力学定律
2. 欧拉运动定律。存档于 2009-07-10。检索日期：2009-03-30。
3. McGill, David J. & King, Wilton W. (1995)。工程力学：动力学导论 (第三版)。PWS 出版社。ISBN 978-0-534-93399-9。
4. 《费曼物理学讲义》卷 I 第 10 章：动量守恒
5. Ho-Kim, Quang；Kumar, Narendra；Lam, Harry C. S. (2004)。现代物理学的邀请 (插图版)。世界科学出版社。第 19 页。ISBN 978-981-238-303-7。
6. Goldstein, 1980, 第 54–56 页。
7. Goldstein, 1980, 第 276 页。
8. Resnick 和 Halliday (1966)，物理学，第 10-3 节。Wiley Toppan，国会图书馆编号 66-11527。
9.Nave, Carl (2010)。“弹性和非弹性碰撞”。Hyperphysics。存档于 2012 年 8 月 18 日。检索于 2012 年 8 月 2 日。
10Serway, Raymond A.; Jewett, John W. Jr. (2012)。物理学原理：基于微积分的教材（第 5 版）。马萨诸塞州波士顿：Brooks/Cole, Cengage Learning。第 245 页。ISBN 978-1-133-10426-1。
11.Nave, Carl (2010)。“汽车碰撞中的力”。Hyperphysics。存档于 2012 年 8 月 22 日。检索于 2012 年 8 月 2 日。
12.Nave, Carl (2010)。“弗兰克-赫兹实验”。Hyperphysics。存档于 2012 年 7 月 16 日。检索于 2012 年 8 月 2 日。
13.McGinnis, Peter M. (2005)。体育与运动生物力学（第 2 版）。伊利诺伊州尚佩恩：Human Kinetics。第 85 页。ISBN 978-0-7360-5101-9。存档于 2016 年 8 月 19 日。
14.Sutton, George (2001)。“第 1 章：分类”。火箭推进元素（第 7 版）。奇切斯特：John Wiley & Sons。ISBN 978-0-471-32642-7。
15.费曼物理学讲义第 I 卷，第 11 章：向量。
16.Rindler 1986，第 26–27 页。
17.Kleppner; Kolenkow。力学导论。第 135–139 页。
18.Goldstein 1980，第 11–13 页。
19.Jackson 1975，第 574 页。
20.费曼物理学讲义第 III 卷，第 21-3 章：两种动量。
21.Goldstein 1980，第 20–21 页。
22.Lerner, Rita G.; Trigg, George L., 编 (2005)。物理学百科全书（第 3 版）。维因海姆：Wiley-VCH。ISBN 978-3-527-40554-1。
23.Goldstein 1980，第 341–342 页。
24.Goldstein 1980，第 348 页。
25.Hand, Louis N.; Finch, Janet D. (1998)。分析力学（第 7 次印刷版）。剑桥：剑桥大学出版社。第 4 章。ISBN 978-0-521-57572-0。
26.Witten, Edward (1981)。“正能量定理的新证明”（PDF）。数学物理通讯。80 (3): 381–402。Bibcode:1981CMaPh..80..381W。doi:10.1007/BF01208277。ISSN 0010-3616。S2CID 1035111。存档于 2016 年 11 月 25 日。检索于 2020 年 12 月 17 日。
27.Grossman, Lisa (2012 年 1 月 18 日)。“挑战死亡的时间晶体可能比宇宙更持久”。新科学家。存档于 2017 年 2 月 2 日。
28.Cowen, Ron (2012 年 2 月 27 日)。“‘时间晶体’可能是一种合法的永动形式”。科学美国人。存档于 2017 年 2 月 2 日。
29.Powell, Devin (2013)。“物质是否可以永远循环变化形状？”。自然。doi:10.1038/nature.2013.13657。ISSN 1476-4687。S2CID 181223762。存档于 2017 年 2 月 3 日。
30.Gibney, Elizabeth (2017)。“时间晶体的探索”。自然。543 (7644): 164–166。Bibcode:2017Natur.543..164G。doi:10.1038/543164a。ISSN 0028-0836。PMID 28277535。S2CID 4460265。存档于 2017 年 3 月 13 日。
31.Tritton 2006，第 48–51 页。
32.费曼物理学讲义第 II 卷，第 40 章：干水的流动。
33.Tritton 2006，第 54 页。
34.Bird, R. Byron; Stewart, Warren; Lightfoot, Edwin N. (2007)。传递现象（第 2 版）。纽约：Wiley。第 13 页。ISBN 978-0-470-11539-8。
35.Tritton 2006，第 58 页。
36.Acheson, D. J. (1990)。初等流体动力学。牛津大学出版社。第 205 页。ISBN 978-0-19-859679-0。
37.Gubbins, David (1992)。地震学与板块构造（重印版）。英国剑桥：剑桥大学出版社。第 59 页。ISBN 978-0-521-37995-3。
38.LeBlond, Paul H.; Mysak, Lawrence A. (1980)。海洋中的波浪（第 2 版）。阿姆斯特丹：Elsevier。第 258 页。ISBN 978-0-444-41926-2。
39.McIntyre, M. E. (1981)。“关于‘波动动量’的神话”。流体力学杂志。106: 331–347。Bibcode:1981JFM...106..331M。doi:10.1017/s0022112081001626。S2CID 18232994。
40.Jackson 1975。
41.Semon, Mark D.; Taylor, John R. (1996 年 11 月)。“对磁矢势的思考”。美国物理学杂志。64 (11): 1361–1369。Bibcode:1996AmJPh..64.1361S。doi:10.1119/1.18400。ISSN 0002-9505。
42.Griffiths, David J. (2017 年 6 月 29 日)。电动力学导论（第 4 版）。英国剑桥：剑桥大学出版社。ISBN 978-1-108-42041-9。OCLC 1021068059。
43.Vieira, R. S.; Brentan, H. B. (2018 年 4 月)。“在狭义相对论框架下的协变引力理论”。欧洲物理学期刊 Plus。133 (4): 165。arXiv:1608.00815。Bibcode:2018EPJP..133..165V。doi:10.1140/epjp/i2018-11988-9。ISSN 2190-5444。S2CID 16691128。
44.Babson, David; Reynolds, Stephen P.; Bjorkquist, Robin; Griffiths, David J. (2009 年 9 月)。“隐藏动量、场动量和电磁冲量”。美国物理学杂志。77 (9): 826–833。Bibcode:2009AmJPh..77..826B。doi:10.1119/1.3152712。ISSN 0002-9505。
45.Griffiths, David J. (2013)。电动力学导论（第 4 版）。波士顿：Pearson。第 361 页。ISBN 978-0-321-85656-2。
46.Jackson 1975，第 238–241 页。文本中给出的高斯单位的表达式，使用附录中表 3 转换为 SI 单位。
47.费曼物理学讲义第二卷第 27-6 章：场动量。
48.Wang, Z. Y. (2016)。“量子力学的广义动量方程”。光学与量子电子学。48 (2): 1–9。doi:10.1007/s11082-015-0261-8。S2CID 124732329。
49.Barnett, Stephen M. (2010)。“阿布拉罕-明科夫斯基困境的解决方案”(PDF)。物理评论快报。104 (7): 070401。Bibcode:2010PhRvL.104g0401B。doi:10.1103/PhysRevLett.104.070401。PMID 20366861。
50.Wang Zhong-Yue; Wang Pin-Yu; Xu Yan-Rong (2011)。“解决阿布拉罕-明科夫斯基争议的关键实验”。Optik。122 (22): 1994–1996。arXiv:1103.3559。Bibcode:2011Optik.122.1994W。doi:10.1016/j.ijleo.2010.12.018。S2CID 119209160。
51.Rindler 1986，第 2 章。
52.费曼物理学讲义第一卷第 15-2 章：洛伦兹变换。
53.Rindler 1986，第 77–81 页。
54.Rindler 1986，第 66 页。
55.Misner, Charles W.; Thorne, Kip S.; Wheeler, John Archibald (1973)。引力。第 24 次印刷。纽约：W. H. Freeman。第 51 页。ISBN 978-0-7167-0344-0。
56.Rindler 1986，第 86–87 页。
57.Rindler, Wolfgang (1991)。狭义相对论导论（第 2 版）。牛津科学出版物。第 82–84 页。ISBN 978-0-19-853952-0。
58."John Philoponus"。斯坦福哲学百科全书。2007 年 6 月 8 日。检索日期：2012 年 7 月 26 日。
59.Espinoza, Fernando (2005)。“对运动概念的历史发展及其对教学影响的分析”。物理教育。40 (2): 141。Bibcode:2005PhyEd..40..139E。doi:10.1088/0031-9120/40/2/002。S2CID 250809354。
60.Nasr, Seyyed Hossein; Razavi, Mehdi Amin (1996)。波斯的伊斯兰知识传统。Routledge。第 72 页。ISBN 978-0-7007-0314-2。
61.Aydin Sayili (1987)。“伊本·西那和布里丹对抛射物运动的研究”。纽约科学院年鉴。500 (1): 477–482。Bibcode:1987NYASA.500..477S。doi:10.1111/j.1749-6632.1987.tb37219.x。S2CID 84784804。
62.Glick, T. F.; Livesay, S. J.; Wallis, F. “Buridan, John”。中世纪科学、技术与医学百科全书。第 107 页。
63.Park, David (1990)。如何与为何：关于物理理论起源与发展的论文。插画：Robin Brickman（第 3 次印刷）。普林斯顿，新泽西州：普林斯顿大学出版社。第 139–141 页。ISBN 978-0-691-02508-7。
64.Descartes, R. (2008) [1644]。Bennett, J. (编)。哲学原理 (PDF)。第二部分，第 36 节。
65.Alexander Afriat (2004)。“笛卡尔与拉格朗日动量”。存档于 2017 年 3 月 9 日，Wayback Machine。
66.Newton, I (1729) [原始作品发表于 1686]。自然哲学的数学原理。译者：Motte, A. 由 Benjamin Motte 出版。第 1–2 页。
67.Garber, Daniel (1992)。“笛卡尔的物理学”。收录于 John Cottingham（编），*剑桥笛卡尔指南*。剑桥：剑桥大学出版社。第 310–319 页。ISBN 978-0-521-36696-0。
68.Rothman, Milton A. (1989)。发现自然法则：物理学的实验基础（第 2 版）。纽约：多佛出版社。第 83–88 页。ISBN 978-0-486-26178-2。
69.Slowik, Edward (2017 年秋季)。“笛卡尔的物理学”。收录于 Zalta, Edward N. (编)，斯坦福哲学百科全书。检索日期：2019 年 11 月 29 日。
70.Taton, Rene, 编 (1964) [1958]。现代科学的起源。Basic Books 出版社。
71.Garber 和 Ayers，第 666–667 页。
72.Garber 和 Ayers，第 689 页。
73.Israel, Jonathan I. (2001 年 2 月 8 日)。激进启蒙：哲学与现代性的形成 1650–1750。牛津大学出版社。第 lxii–lxiii 页。ISBN 978-0-19-162287-8。检索日期：2013 年 5 月 11 日。
74.Dictionary，第 470 页。
75.Scott, J. F. (1981)。约翰·沃利斯的数学著作。Chelsea Publishing Company。第 111 页。ISBN 978-0-8284-0314-6。
76.Leibniz, G. W. (1989)。“形而上学的讨论”。收录于 Ariew, Roger; Garber, Daniel (编)。哲学随笔。印第安纳波利斯，印第安纳州：Hackett 出版社。第 49–51 页。ISBN 978-0-87220-062-3。
77.Grimsehl, Ernst (1932)。物理学教材。翻译：Woodward, Leonard Ary。伦敦与格拉斯哥：Blackie & Son。第 78 页。
78.Rescigno, Aldo (2003)。*药代动力学基础*。纽约：Kluwer Academic/Plenum 出版社。第 19 页。ISBN 978-0-306-47704-1。
79.Jennings, John (1721)。Miscellanea in Usum Juventutis Academicae（拉丁文）。北安普顿：R. Aikes & G. Dicey。第 67 页。

8. 书目

Halliday, David; Resnick, Robert (2013 年 8 月 13 日)。*Fundamentals of Physics*。John Wiley & Sons 出版社。第 9 章。ISBN 978-1-118-23071-8。
Dugas, René (1988)。*A history of mechanics*。由 J.R. Maddox 翻译为英文（Dover 版）。纽约：Dover Publications 出版社。ISBN 978-0-486-65632-8。
Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (2005)。*The Feynman lectures on physics, Volume 1: Mainly Mechanics, Radiation, and Heat*（最终版）。旧金山：Pearson Addison-Wesley 出版社。ISBN 978-0-8053-9046-9。
Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (2006)。*The Feynman lectures on physics*（最终版）。旧金山：Pearson Addison-Wesley 出版社。ISBN 978-0-8053-9047-6。
Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (2005)。*The Feynman lectures on physics, Volume III: Quantum Mechanics*（最终版）。纽约：BasicBooks 出版社。ISBN 978-0-8053-9049-0。
Goldstein, Herbert (1980)。*Classical mechanics*（第二版）。马萨诸塞州雷丁：Addison-Wesley 出版公司。ISBN 978-0-201-02918-5。
Hand, Louis N.; Finch, Janet D. *Analytical Mechanics*。剑桥大学出版社。第 4 章。
Jackson, John David (1975)。*Classical electrodynamics*（第二版）。纽约：Wiley 出版社。ISBN 978-0-471-43132-9。
Jammer, Max (1999)。*Concepts of force: a study in the foundations of dynamics*（复刻版）。纽约州矿山：Dover Publications 出版社。ISBN 978-0-486-40689-3。
Landau, L.D.; Lifshitz, E.M. (2000)。*The classical theory of fields*。英文版，带有修订；由 Morton Hamermesh 从俄文翻译（第四版）。牛津：Butterworth Heinemann 出版社。ISBN 978-0-7506-2768-9。
Rindler, Wolfgang (1986)。*Essential Relativity: Special, general and cosmological*（第二版）。纽约：Springer 出版社。ISBN 978-0-387-10090-6。
Serway, Raymond; Jewett, John (2003)。*Physics for Scientists and Engineers*（第 6 版）。Brooks Cole 出版社。ISBN 978-0-534-40842-8。
Stenger, Victor J. (2000)。*Timeless Reality: Symmetry, Simplicity, and Multiple Universes*。Prometheus Books 出版社。第 12 章尤为重要。
Tipler, Paul (1998)。*Physics for Scientists and Engineers: Vol. 1: Mechanics, Oscillations and Waves, Thermodynamics*（第 4 版）。W.H. Freeman 出版社。ISBN 978-1-57259-492-0。
Tritton, D.J. (2006)。*Physical fluid dynamics*（第二版）。牛津：Clarendon Press 出版社。第 58 页。ISBN 978-0-19-854493-7。

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。