皮埃尔-西蒙·拉普拉斯（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 皮埃尔-西蒙·拉普拉斯（Pierre-Simon, Marquis de Laplace，1749 年 3 月 23 日－1827 年 3 月 5 日）是法国学者，他的工作对工程学、数学、统计学、物理学、天文学和哲学的发展具有重要意义。他在五卷本《天体力学》（Mécanique céleste）（1799–1825）中总结并扩展了前人的工作。这部著作将经典力学的几何学研究转化为基于微积分的研究，从而开辟了更广泛的研究领域。[2]拉普拉斯还推广并进一步确认了艾萨克·牛顿爵士的工作。在统计学中，贝叶斯概率解释主要是由拉普拉斯发展而来的。[3]

　　 拉普拉斯提出了拉普拉斯方程，并开创了拉普拉斯变换，这在数学物理的许多分支中都有应用，而数学物理领域正是他主导发展的一个重要领域。广泛应用于数学中的拉普拉斯算子也以他的名字命名。他重新阐述并发展了太阳系起源的星云假说，是最早提出类似黑洞概念的科学家之一，[4] 斯蒂芬·霍金曾表示：“拉普拉斯基本上预言了黑洞的存在”。[1]他提出了拉普拉斯恶魔，这是一个假设的全能预测智慧。他还改进了牛顿关于声速的计算，得出了更精确的测量结果。[5]

　　 拉普拉斯被认为是历史上最伟大的科学家之一。有时被称为 “法国的牛顿” 或 “法国的牛顿”，他被描述为拥有卓越的数学天赋，超越了几乎所有同时代的人。[6] 1785 年，拉普拉斯曾担任拿破仑从巴黎军事学院毕业时的考官。[7] 拉普拉斯于 1806 年成为帝国伯爵，并在 1817 年波旁王朝复辟后被封为侯爵。

1. 早年

　　 拉普拉斯生活中的一些细节不为人知，因为 1925 年与他的曾曾孙科尔贝尔-拉普拉斯伯爵的家族 château（位于利厄市附近的圣朱利安·德·梅约）一起被烧毁。还有一些记录早在 1871 年，当他的位于巴黎附近阿尔居伊的住所被掠夺时就已被销毁。[8]

　　 拉普拉斯于 1749 年 3 月 23 日出生在诺曼底的博蒙-昂-奥热（Beaumont-en-Auge），这个小村庄位于 Pont l'Évêque 以西约四英里处。根据 W. W. Rouse Ball 的说法，[9] 他的父亲皮埃尔·德·拉普拉斯（Pierre de Laplace）拥有并耕种着马尔基斯的小庄园。他的曾叔父奥利维尔·德·拉普拉斯（Maitre Oliver de Laplace）曾担任皇家外科医生。似乎他从一名学生逐渐升职为博蒙学校的监督员；但在获得了给达朗贝尔（d'Alembert）的介绍信后，他前往巴黎以谋求更好的发展。然而，卡尔·皮尔逊（Karl Pearson）对 Rouse Ball 叙述中的不准确之处进行了严厉批评，并指出：

　　 的确，在拉普拉斯时代，卡昂可能是诺曼底所有城市中最具知识活力的地方。正是在这里，拉普拉斯接受了教育，并暂时担任教授。也是在这里，他写下了发表在都灵皇家学会《混合文集》中的第一篇论文，卷四，1766-1769 年，至少比他 22 或 23 岁时前往巴黎的 1771 年早了两年。因此，在他不到 20 岁时，他已经与位于都灵的拉格朗日保持联系。他并不是一个仅有农民背景的未经教化的乡村小伙子，贸然前往巴黎！1765 年，16 岁的拉普拉斯离开了博蒙的 “奥尔良公爵学校”，前往卡昂大学，他似乎在这里学习了五年，并且是斯芬克斯社团的成员。博蒙的军事学校直到 1776 年才取代了这所旧学校。

　　 他的父母，皮埃尔·拉普拉斯和玛丽-安妮·索雄，来自较为富裕的家庭。拉普拉斯家族至少在 1750 年之前一直从事农业，但皮埃尔·拉普拉斯（父亲）还是一位苹果酒商人和博蒙镇的市政官。

　　 皮埃尔·西蒙·拉普拉斯曾就读于该村的一所由本笃会修道院经营的学校，他的父亲原本打算让他成为天主教会的神职人员。16 岁时，为了进一步实现父亲的意图，他被送往卡昂大学学习神学。[10]

　　 在大学期间，他受到两位热衷数学的教师克里斯托夫·加德布莱和皮埃尔·勒卡努的指导，正是他们激发了他对该学科的热情。在这里，拉普拉斯作为数学家的才华迅速得到了认可，并且在仍在卡昂时，他写下了《关于无穷小和有限差分的积分计算的论文》。这篇论文也标志着拉普拉斯与拉格朗日之间的第一次通信。拉格朗日比拉普拉斯年长十三岁，最近在他故乡都灵创办了一本名为《都灵文集》（Miscellanea Taurinensia）的期刊，许多他的早期作品都刊登在其中，拉普拉斯的论文正是在该系列的第四卷中发表的。大约在这个时候，拉普拉斯意识到自己并没有成为神职人员的天赋，于是决定成为一名职业数学家。有些资料指出，他此后与教会决裂并成为无神论者。[需要引用] 拉普拉斯没有获得神学学位，而是带着勒卡努写给让·勒朗·达朗贝尔的介绍信前往巴黎，而达朗贝尔在当时是科学界的权威。[10][11]

　　 根据他的曾曾孙的说法，[8] 达朗贝尔最初对拉普拉斯的接待并不好，为了摆脱他，他给了拉普拉斯一本厚厚的数学书，说让他读完后再回来。几天后，当拉普拉斯回来时，达朗贝尔更为冷淡，并且没有掩饰他对拉普拉斯不可能读懂并理解那本书的看法。但在与拉普拉斯交谈后，达朗贝尔意识到拉普拉斯确实理解了书中的内容，从那时起，他开始对拉普拉斯给予指导。

　　 另一种说法是，拉普拉斯在一夜之间解决了达朗贝尔要求他提交的下周的问题，然后在接下来的夜晚又解决了一个更难的问题。达朗贝尔对此印象深刻，并推荐他进入军事学院任教。[12]

　　 有了稳定的收入和不太苛求的教学任务，拉普拉斯开始全身心投入原创研究，在接下来的十七年里（1771 年至 1787 年），他在天文学领域创作了大量原创性作品。[13]

　　 从 1780 年到 1784 年，拉普拉斯与法国化学家安托万·拉瓦锡（Antoine Lavoisier）合作进行了一些实验研究，为这些任务设计了自己的设备。[14] 1783 年，他们共同发表了论文《关于热的回忆录》，在其中讨论了分子运动的动理论。[15] 在他们的实验中，他们测量了不同物体的比热和金属在温度升高时的膨胀情况。他们还测量了乙醇和醚在压力下的沸点。

　　 拉普拉斯进一步给孔多塞侯爵留下了深刻的印象，早在 1771 年，拉普拉斯便觉得自己有资格加入法国科学院。然而，那一年，学籍被授予了亚历山大-泰奥菲尔·范德蒙德（Alexandre-Théophile Vandermonde），1772 年则授予了雅克·安托万·约瑟夫·库桑（Jacques Antoine Joseph Cousin）。拉普拉斯对此感到不满，1773 年初，达朗贝尔写信给位于柏林的拉格朗日，询问是否可以为拉普拉斯找到一个职位。然而，孔多塞于 2 月成为了科学院的常任秘书，拉普拉斯在 3 月 31 日被选为院士候补成员，时年 24 岁。[16] 1773 年，拉普拉斯在法国科学院前宣读了他的关于行星运动不变性的论文。同年 3 月，他被选为学院成员，之后他在该学术机构进行了大部分的科学研究。[17]

　　 在 1788 年 3 月 15 日，拉普拉斯（Laplace）在 39 岁时娶了来自贝桑松一个 “良好” 家庭的 18 岁女孩玛丽-夏洛特·德·库尔蒂·德·罗曼热（Marie-Charlotte de Courty de Romanges）。婚礼在巴黎的圣叙尔皮斯教堂举行。夫妻俩有一个儿子，查尔斯-埃米尔（1789–1874），和一个女儿，索菲-苏珊娜（1792–1813）。

2. 分析、概率与天文稳定性

　　 拉普拉斯的早期发表作品始于 1771 年，主要涉及微分方程和有限差分，但他已经开始思考概率和统计的数学及哲学概念。[22] 然而，在 1773 年当选为法兰西科学院成员之前，他已经草拟了两篇论文，这些论文为他建立了声誉。第一篇论文《通过事件的概率推测因果关系》最终于 1774 年发表，第二篇论文则在 1776 年发表，进一步阐述了他的统计思想，并开始了他对天体力学和太阳系稳定性的系统研究。这两个学科始终在他的思维中紧密相连。“拉普拉斯将概率作为修正知识缺陷的工具。”[23] 拉普拉斯关于概率和统计的工作将在下文中讨论，包括他关于概率解析理论的成熟工作。

太阳系的稳定性

　　 艾萨克·牛顿爵士于 1687 年出版了《自然哲学的数学原理》（Philosophiæ Naturalis Principia Mathematica），在其中他根据自己的运动定律和万有引力定律推导出了开普勒定律，描述了行星的运动。然而，尽管牛顿在私下里已经发展了微积分方法，他的所有公开作品仍然使用繁琐的几何推理，这种方法并不适合解释行星间相互作用的更微妙的高阶效应。牛顿本人曾怀疑是否有可能找到整个问题的数学解法，甚至认为定期的神力干预是保证太阳系稳定所必需的。摒弃神力干预的假设将成为拉普拉斯科学生涯中的一项重大任务。[24] 现在普遍认为，尽管拉普拉斯的方法对理论的发展至关重要，但仅凭这些方法并不足够精确以证明太阳系的稳定性；今天我们理解太阳系在精细尺度上通常是混乱的，尽管在粗尺度上目前相对稳定。[25]: 83, 93

　　 天文学中的一个特定问题是木星的轨道似乎在缩小，而土星的轨道在扩展。这个问题曾被莱昂哈德·欧拉于 1748 年和约瑟夫·路易·拉格朗日于 1763 年尝试解决，但都未成功。[26] 1776 年，拉普拉斯发表了一篇论文，首次探讨了假设的光以太或不瞬时作用的引力定律可能的影响。最终，他回到了对牛顿引力的知识投资。[27] 欧拉和拉格朗日通过忽略运动方程中的小项，做出了一个实际的近似。拉普拉斯注意到，尽管这些项本身很小，但当它们在时间上积累时，可能会变得重要。拉普拉斯将他的分析扩展到了更高阶的项，直到包括三次项。通过这种更精确的分析，拉普拉斯得出结论，任何两颗行星和太阳必须处于相互平衡中，从而开启了他对太阳系稳定性的研究。[28] 杰拉尔德·詹姆斯·惠特罗称这一成就为 “自牛顿以来物理天文学中最重要的进展”。[24]

　　 拉普拉斯对所有科学都有广泛的知识，并主导了法兰西科学院的所有讨论。[29] 拉普拉斯似乎仅将分析视为解决物理问题的一种手段，尽管他发明所需分析的能力几乎是惊人的。只要他的结果是正确的，他对解释他得出这些结果的过程几乎不做任何努力；他从不研究过程中的优雅或对称性，对他来说，只要能以任何方式解决他所讨论的特定问题就足够了。[13]

3. 潮汐动力学

潮汐的动态理论

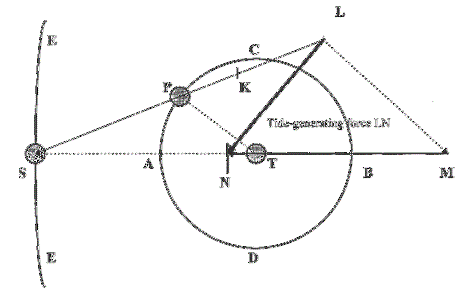
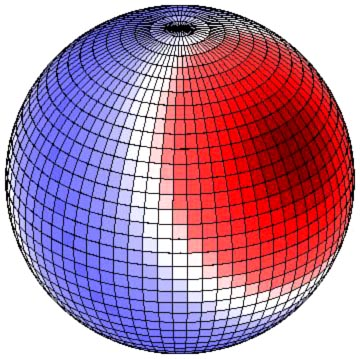
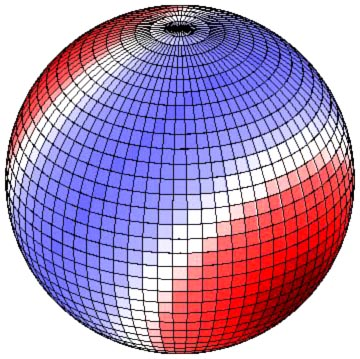
　　 虽然牛顿通过描述潮汐产生力来解释潮汐现象，伯努利则描述了地球上水体对潮汐势的静态反应，拉普拉斯于 1775 年发展出的潮汐动态理论[30] 描述了海洋对潮汐力的真实反应。[31] 拉普拉斯的海洋潮汐理论考虑了摩擦、共振和海洋盆地的自然周期。它预测了全球海洋盆地中大的安菲德罗米克系统，并解释了实际观测到的海洋潮汐。[32][33]

　　 基于太阳和月球引力梯度的平衡理论，忽略了地球的自转、大陆的影响及其他重要因素，无法解释真实的海洋潮汐。[34][35][36][32][37][38][39][40][41]

　　 由于测量结果已证实该理论，现在许多现象有了可能的解释，例如潮汐如何与深海脊和海山链相互作用，从而产生深层漩涡，将营养物质从深海输送到海面。[42] 平衡潮汐理论计算出的潮汐波高度不到半米，而动态理论则解释了潮汐为什么能达到 15 米。[43] 卫星观测证实了动态理论的准确性，全球的潮汐现已被测量到几厘米的误差范围内。[44][45] 来自 CHAMP 卫星的测量结果与基于 TOPEX 数据的模型非常吻合。[46][47][48] 全球潮汐的准确模型对研究至关重要，因为在计算重力和海平面变化时，必须从测量中去除潮汐引起的变化。[49]

拉普拉斯的潮汐方程

　　 1776 年，拉普拉斯提出了一组描述潮汐流动的线性偏微分方程，潮汐流被描述为一种条形流动的二维薄层流动。引入了科氏效应以及由引力引起的侧向强迫力。拉普拉斯通过简化流体动力学方程获得了这些方程，但它们也可以通过拉格朗日方程从能量积分推导出来。

　　 对于平均厚度为 \( D \) 的流体薄层，垂直潮汐升高 \( \zeta \) 以及水平方向速度分量 \( u \) 和 \( v \)（分别在纬度 \( \varphi \) 和经度 \( \lambda \) 方向上）满足拉普拉斯的潮汐方程：[50] \[ \frac{\partial \zeta}{\partial t} + \frac{1}{a \cos\left(\varphi\right) } \left[ \frac{\partial}{\partial \lambda} (uD) + \frac{\partial}{\partial \varphi} \left( vD \cos\left(\varphi\right) \right) \right] = 0,~ \] \[ \frac{\partial u}{\partial t} - v \left( 2 \Omega \sin\left(\varphi\right) \right) + \frac{1}{a \cos\left(\varphi\right) } \frac{\partial}{\partial \lambda} \left( g \zeta + U \right) = 0 \quad \text{and}~ \] \[ \frac{\partial v}{\partial t} + u \left( 2 \Omega \sin\left(\varphi\right) \right) + \frac{1}{a} \frac{\partial}{\partial \varphi} \left( g \zeta + U \right) = 0,~ \] 其中，\( \Omega \) 是行星自转的角频率，\( g \) 是行星在平均海洋表面的重力加速度，\( a \) 是行星半径，\( U \) 是外部引力潮汐强迫势。

　　 威廉·汤姆森（开尔文勋爵）使用旋度重新写出了拉普拉斯的动量项，从而得出了一个涡度方程。在某些条件下，这可以进一步重写为涡度守恒方程。

4. 关于地球的形状

　　 在 1784 年至 1787 年期间，他发表了一些具有非凡影响力的论文。其中最重要的一篇是在 1783 年宣读的，并于 1784 年作为《行星的运动与椭圆形状理论》第二部分再版，同时也收录在《天体力学》第三卷中。在这项工作中，拉普拉斯完全确定了一个椭球体对其外部粒子的引力。这一成果因引入了球面调和函数或拉普拉斯系数而值得记住，同时也促进了我们现在所称的引力势在天体力学中的应用发展。

球面调和函数

　　 在 1783 年，阿德里安-马里·勒让德在一篇提交给法兰西科学院的论文中引入了现在所称为关联勒让德函数。[13] 如果平面中的两个点具有极坐标 \((r, \theta)\) 和 \((r', \theta')\)，其中 \(r' \geq r\)，则通过基本的代数变换，可以将这两个点之间距离 \(d\) 的倒数表示为： \[ \frac{1}{d} = \frac{1}{r'} \left[ 1 - 2 \cos\left(\theta' - \theta\right) \frac{r}{r'} + \left( \frac{r}{r'} \right)^2 \right]^{-\frac{1}{2}}.~ \] 这个表达式可以使用牛顿的广义二项式定理展开为 \(r/r'\) 的幂级数，得到： \[ \frac{1}{d} = \frac{1}{r'} \sum_{k=0}^{\infty} P_k^0 ( \cos\left(\theta' - \theta\right) ) \left( \frac{r}{r'} \right)^k.~ \] 函数序列 \( P_k^0(\cos \varphi) \) 是所谓的 “关联勒让德函数” 集合，它们的实用性来源于这样一个事实：圆上每个点的函数都可以展开为这些函数的级数。[13]

　　 拉普拉斯在几乎没有给予勒让德应有的信用的情况下，将这一结果扩展到三维空间，从而得出了一个更一般的函数集——球面调和函数或拉普拉斯系数。后一术语现在不常使用。[13]：第 340 页及后续

势理论

　　 这篇论文还因发展了标量势的概念而值得注意。[13] 在现代语言中，作用于物体的引力是一个向量，具有大小和方向。势函数是一个标量函数，它定义了这些向量如何变化。与向量函数相比，标量函数在计算和概念上更容易处理。

　　 亚历克西·克莱劳特（Alexis Clairaut）在 1743 年首次提出了这一概念，当时他在处理一个类似的问题，尽管他使用的是牛顿类型的几何推理。拉普拉斯将克莱劳特的工作描述为 “最美丽的数学成果之一”。[51] 然而，罗素·鲍尔（Rouse Ball）声称，这个想法 “是从约瑟夫·路易·拉格朗日（Joseph Louis Lagrange）那里借用的，后者在 1773 年、1777 年和 1780 年的论文中使用了这一概念”。[13] “势” 这一术语本身是丹尼尔·伯努利（Daniel Bernoulli）提出的，他在 1738 年的《流体力学》论文中引入了这一术语。然而，根据罗素·鲍尔的说法，直到乔治·格林（George Green）在 1828 年发表的《数学分析在电磁理论中的应用》一文中，才真正使用了 “势函数” 这一术语（指代拉普拉斯意义上的空间坐标函数 \( V \)）。[52][53]

　　 拉普拉斯将微积分的语言应用于势函数，并证明它总是满足以下微分方程：[13] \[ \nabla^2 V = \frac{\partial^2 V}{\partial x^2} + \frac{\partial^2 V}{\partial y^2} + \frac{\partial^2 V}{\partial z^2} = 0.~ \] 类似的结果早些年由莱昂哈德·欧拉（Leonhard Euler）得到，针对的是流体的速度势。[54][55]

　　 拉普拉斯随后关于引力的研究基于这一结果。量 \(\nabla^2 V\) 被称为 \(V\) 的集中度，其在任意点的值表示该点 \(V\) 值相对于该点邻域中的平均值的 “过剩”[56]。拉普拉斯方程，作为泊松方程的特例，在数学物理中无处不在。势的概念出现在流体动力学、电磁学以及其他领域。罗素·鲍尔（Rouse Ball）推测，这可以被看作是康德（Kant）感知理论中 “先天形式” 的一种 “外在标志”[13]。

　　 球面调和函数对拉普拉斯方程的实际解至关重要。拉普拉斯方程在球坐标系下（如用于绘制天空图的坐标系统）可以通过分离变量法简化为一个依赖于与中心点距离的径向部分和一个角度或球面部分。球面部分的解可以表示为拉普拉斯的球面调和函数级数，从而简化实际计算。

5. 行星和月球不等式

木星-土星大不等式

　　 拉普拉斯在 1784 年、1785 年和 1786 年分三部分提出了关于行星不等式的论文。该论文主要涉及识别和解释现在称为 “木星-土星大不等式” 的扰动。拉普拉斯解决了长期以来在研究和预测这些行星运动中的一个问题。他首先通过一般性考虑，证明了两个行星的相互作用永远不会导致它们轨道的偏心率和倾斜度发生大的变化；然而，更重要的是，他还指出，由于木星和土星的平均运动接近成比关系，这种特殊性在木星-土星系统中产生了。[6][57]

　　 在这个背景下，"成比关系"意味着两个行星的平均运动比率几乎等于一对小整数之间的比率。土星围绕太阳的轨道周期几乎等于木星的五个周期。相应的，平均运动的倍数差（2nJ − 5nS）对应一个近 900 年的周期，这个周期在与这个相同周期的小扰动力的积分中作为一个小的除数出现。因此，具有这个周期的积分扰动非常大，土星的轨道经度扰动约为 0.8°，木星约为 0.3°。

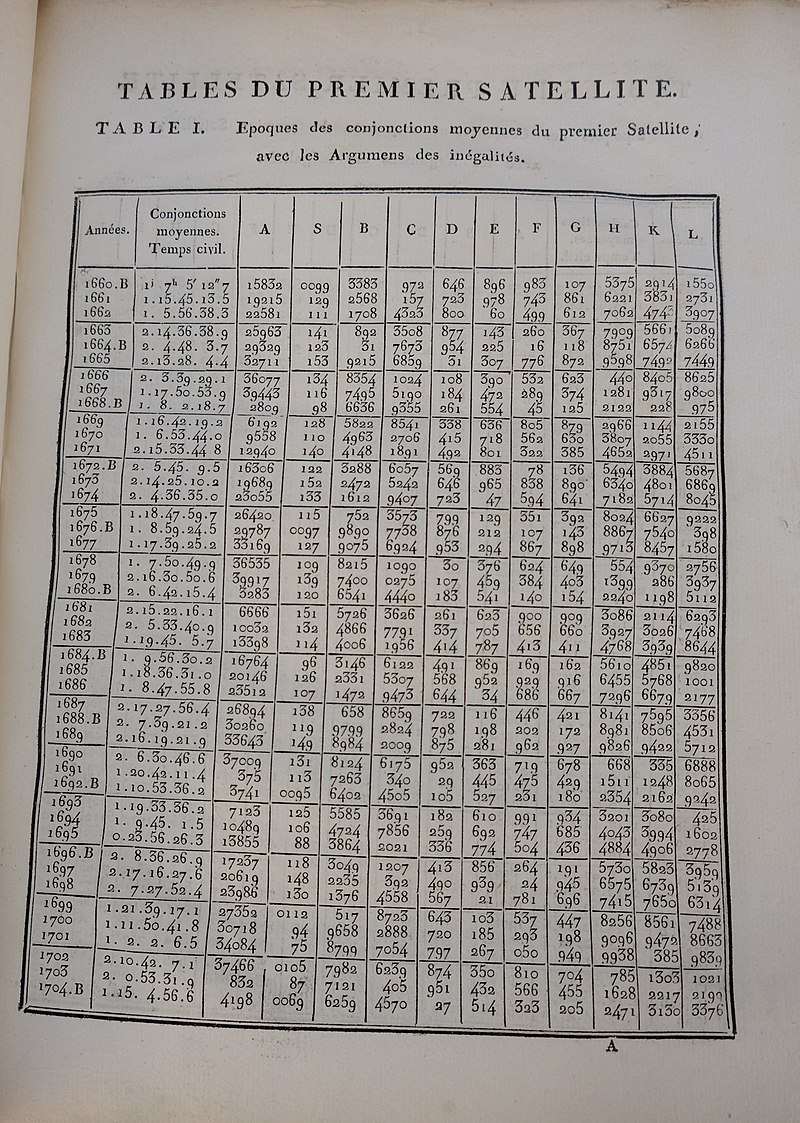
　　 拉普拉斯在 1788 年和 1789 年的两篇论文中进一步发展了这些关于行星运动的定理，但借助拉普拉斯的发现，木星和土星的运动表终于可以更加精确地制作。基于拉普拉斯的理论，德拉布尔（Delambre）计算出了他的天文表。[13]

书籍

　　 拉普拉斯现在将自己定下任务，编写一部作品，旨在 “为太阳系这一伟大的力学问题提供完整的解决方案，并使理论与观测尽可能吻合，以至于经验公式不再在天文表中占有一席之地。” 其成果体现在《世界体系概述》（Exposition du système du monde）和《天体力学》（Mécanique céleste）中。

　　 前者于 1796 年出版，提供了对现象的一般解释，但省略了所有细节。它包含了天文学历史的概述。这个概述为作者赢得了进入法兰西科学院 40 名成员的荣誉，并被普遍认为是法国语言文学的杰作之一，尽管它在处理后期天文学内容时并不完全可靠。

　　 拉普拉斯发展了行星系统形成的星云假说，该假说最早由伊曼纽尔·斯威登堡（Emanuel Swedenborg）提出，并由伊曼纽尔·康德（Immanuel Kant）扩展。这个假说至今仍然是研究行星系统起源的最广泛接受的模型。根据拉普拉斯对这一假说的描述，太阳系由一个旋转的发光气体球体演化而来，这个气体球体围绕其质心轴旋转。随着其冷却，这个气体球体收缩，连续的环带从其外缘脱落。这些环带又冷却，最终凝聚成行星，而太阳则代表着剩下的中央核心。根据这一观点，拉普拉斯预测，较远的行星将比靠近太阳的行星更古老。

　　 如前所述，星云假说的概念早在 1755 年就由康德提出，[58]他还建议了 “流星聚集” 和潮汐摩擦作为影响太阳系形成的原因。拉普拉斯很可能知道这一点，但像他那个时代的许多作家一样，他通常不引用他人的工作。[8]

　　 拉普拉斯对太阳系的分析性讨论载于他的《天体力学》（Mécanique céleste），该书分为五卷。前两卷于 1799 年出版，内容包括行星运动的计算方法、行星形状的确定以及潮汐问题的求解方法。[6] 第三卷和第四卷分别于 1802 年和 1805 年出版，包含了这些方法的应用以及若干天文表。第五卷于 1825 年出版，主要是历史性的，但作为附录给出了拉普拉斯最新研究的成果。《天体力学》包含了拉普拉斯的许多个人研究，但其中许多结果是借用其他作家的成果，且几乎没有提及来源。该书的结论，被历史学家描述为其他作家和拉普拉斯一百年努力的组织性成果，拉普拉斯却将其呈现为仅属于他自己的发现。[13]

　　 让-巴蒂斯特·比奥（Jean-Baptiste Biot），在协助拉普拉斯修订《天体力学》时表示，拉普拉斯自己常常无法回忆起推理过程中的细节，如果确信结论是正确的，他便满足于插入一句话：“Il est àisé à voir que...”（“显而易见的是……”）。《天体力学》不仅是牛顿《自然哲学的数学原理》的微分学语言翻译，而且完成了牛顿未能填补的部分细节。这部著作在费利克斯·蒂塞朗（Félix Tisserand）的《天体力学教程》（1889–1896）中得到了更精细的呈现，但拉普拉斯的这部著作依然是标准的权威之作。[13] 在 1784 至 1787 年间，拉普拉斯发表了一些具有卓越影响力的论文。其中重要的论文之一发表于 1784 年，并在《天体力学》第三卷中再版。[需要引用] 在这部作品中，他完全确定了一个椭球体对其外部粒子的引力。这一工作因将 “势” 引入分析中而闻名，这一数学概念在物理科学中具有广泛的应用。

6. 光学

　　 拉普拉斯支持牛顿的光子理论。在《天体力学》第四版中，拉普拉斯假设短程分子力是负责光子折射的原因。[59] 拉普拉斯和埃蒂安-路易·马吕斯（Étienne-Louis Malus）还证明了，光的双折射现象可以通过最小作用原理从光子中恢复出惠更斯原理。[60]

　　 然而，1815 年，奥古斯丁-让·弗雷内尔（Augustin-Jean Fresnel）提出了一种新的衍射波动理论，并在弗朗索瓦·阿拉戈（François Arago）的帮助下将其提交给法国科学院的委员会。拉普拉斯是委员会成员之一，最终他们授予弗雷内尔奖项，以表彰他的新理论。[61]: I.108 

引力对光的影响

　　 通过使用光子理论，拉普拉斯还接近于提出黑洞的概念。他认为引力可以影响光，并且可能存在一些巨大的恒星，其引力如此之大，以至于光也无法从其表面逃逸（参见逃逸速度）。[62][1][63][64] 然而，这一见解超前于当时的科学发展，因而在科学史上并未发挥作用。[65]

7. 阿尔库伊

　　 1806 年，拉普拉斯在阿尔库伊购买了一座房子，当时阿尔库伊还是一个村庄，尚未并入巴黎的都市区。化学家克劳德·路易·贝尔托莱特是他的邻居——他们的花园没有隔开[66]——两人形成了一个非正式的科学圈子，后来被称为阿尔库伊学会。由于与拿破仑的亲近关系，拉普拉斯和贝尔托莱特实际上掌控了科学界的晋升和更高职位的入选。该学会建立了一个复杂的赞助金字塔[67]。1806 年，拉普拉斯还被选为瑞典皇家科学院的外籍会员。

8. 概率的解析理论

　　 1812 年，拉普拉斯发布了他的《概率的解析理论》（Théorie analytique des probabilités），在其中他提出了许多统计学的基本结果。该论文的前半部分涉及概率方法和问题，后半部分则讨论了统计方法和应用。按照后来的标准，拉普拉斯的证明并不总是严格的，他的观点在贝叶斯与非贝叶斯视角之间来回摇摆，这使得一些研究难以跟随，但即使在一些分析出错的情况下，他的结论仍然是基本正确的[68]。1819 年，他出版了关于概率的通俗读物。这本书与《概率理论》的关系，正如《世界体系》与《天体力学》的关系一样[13]。在强调概率问题的分析重要性，特别是在 “大数法则公式函数的逼近” 这一背景下，拉普拉斯的工作超越了当时几乎完全关注实际应用方面的观点[69]。拉普拉斯的《概率的解析理论》直到 19 世纪末仍是最具影响力的数学概率理论著作。尽管拉普拉斯的误差理论对统计学的普遍相关性直到 19 世纪末才得到充分理解，但它对概率理论的进一步发展，尤其是在分析导向的方向上，产生了深远影响。

归纳概率

　　 在他的《哲学随笔：关于概率的思考》（Essai philosophique sur les probabilités，1814 年）中，拉普拉斯提出了一种基于概率的数学归纳推理系统，今天我们称之为贝叶斯推理。他以一系列概率原理开篇，其中前七条是：

1. 概率是 “有利事件” 与所有可能事件的比值。
2. 第一个原理假定所有事件的概率相等。当这一假设不成立时，我们必须首先确定每个事件的概率。然后，概率就是所有可能的有利事件概率之和。
3. 对于独立事件，所有事件发生的概率是各事件概率的乘积。
4. 当事件 A 和 B 相互依赖时，复合事件的概率是事件 A 的概率与在事件 A 发生的条件下事件 B 发生的概率的乘积。
5. 事件 A 发生的概率，给定事件 B 已经发生，等于 A 和 B 同时发生的概率除以事件 B 的概率。
6. 对第六个原理有三个推论，这些推论构成了贝叶斯规则。假设事件 Ai ∈ {A1, A2, ... An}列举了事件 B 的所有可能原因，那么： \[ \Pr(A_{i}\mid B) = \Pr(A_{i}) \frac{\Pr(B \mid A_{i})}{\sum _{j} \Pr(A_{j}) \Pr(B \mid A_{j})}~ \]
7. 未来事件 C 的概率是从观察到的事件 A 中选择每个原因 Bi 的概率与在该原因存在的条件下未来事件发生的概率的乘积之和。用符号表示为： \[ \Pr(C|A) = \sum _{i} \Pr(C|B_{i}) \Pr(B_{i}|A)~ \]”

　　 他的系统中一个著名的公式是‘继承法则’，它在第七条原理中给出。假设某次试验只有两个可能的结果，分别标记为‘成功’和‘失败’。假设我们对结果的相对可能性几乎或完全没有先验知识，拉普拉斯推导出了下一个试验成功的概率公式： \[ \Pr(\text{下一个结果是成功}) = \frac{s+1}{n+2}~ \] 其中，\(s\) 是先前观察到的成功次数，\(n\) 是总的观察试验次数。这个公式仍然作为事件概率的估算器，当我们知道事件空间，但样本数量较少时，依然适用。

　　 继承法则一直受到许多批评，部分原因在于拉普拉斯用来说明该法则的例子。他计算了太阳明天会升起的概率，假设过去它从未失败过： \[ \Pr(\text{太阳明天升起}) = \frac{d+1}{d+2}~ \] 其中，\(d\) 是太阳过去升起的次数。这个结果被讽刺为荒谬，有些作者因此得出结论，认为继承法则的所有应用都是荒谬的。然而，拉普拉斯完全意识到这个结果的荒谬性；在这个例子后，他写道：“但是，这个数字（即太阳明天升起的概率）对那些看到万象中调控日夜与季节的原则的人来说，远大于对他人的数字，因为他们意识到此刻没有什么能够阻止它的进程。”[70]

概率生成函数

　　 拉普拉斯在 1779 年写的一篇论文中曾指出过估算有利事件数与所有可能事件数之比的方法。这个方法是将任何函数的连续值视为另一个函数在不同变量下展开的系数。因此，后者被称为前者的概率生成函数。拉普拉斯随后展示了如何通过插值法从生成函数中确定这些系数。接着，他解决了反向问题，从系数中找到生成函数；这个过程通过求解有限差分方程来实现。

最小二乘法与中心极限定理

　　 本论文的第四章包括了最小二乘法的阐述，这充分展示了拉普拉斯在分析过程中的精湛掌握。1805 年，勒让德（Legendre）发表了最小二乘法，但并未尝试将其与概率理论联系起来。1809 年，高斯（Gauss）从算术平均值最可能表示所测量量的观点推导出了正态分布；随后，他将这一论证自我反转，证明了如果观察误差服从正态分布，最小二乘法估计会给出回归分析中系数的最可能值。这两项工作似乎激发了拉普拉斯完成他早在 1783 年就考虑过的概率论论文的工作。

　　 在 1810 年和 1811 年的两篇重要论文中，拉普拉斯首次发展了特征函数，作为大样本理论的工具，并证明了第一个一般性的中心极限定理。然后，在他看到高斯的工作后，他在 1810 年论文的补充部分中展示了中心极限定理为最小二乘法提供了贝叶斯的正当性：如果我们合并多个观察值，而每个观察值本身都是大量独立观察的平均值，那么最小二乘法估计不仅最大化了似然函数（视为后验分布），还最小化了期望的后验误差，所有这些都不依赖于对误差分布的假设或算术平均原理的循环应用。[68] 1811 年，拉普拉斯采取了不同的非贝叶斯方法。考虑到一个线性回归问题，他将注意力集中在线性系数的线性无偏估计量上。在证明当观察数量足够大时，该类估计量大致服从正态分布后，他认为最小二乘法提供了 “最佳” 的线性估计量。在这里，“最佳” 是指最小化渐近方差，从而既最小化了误差的期望绝对值，又最大化了估计值落在任何关于未知系数的对称区间内的概率，无论误差分布如何。他的推导包括了最小二乘估计两个参数的联合极限分布。[68]

9. 拉普拉斯的恶魔

　　 1814 年，拉普拉斯发表了可能是第一次科学地阐述因果决定论的观点：[71]

　　 我们可以将宇宙的当前状态视为其过去的结果和未来的原因。如果有一个智慧存在，在某一时刻能够知道所有使自然运动的力量，以及自然中所有物体的位置，如果这个智慧存在还足够强大，能够对这些数据进行分析，那么它将能够用一个公式涵盖宇宙中最大物体和最微小原子的运动；对于这样的智慧存在来说，什么都不再是不确定的，未来就像过去一样，对于它而言，未来就是现在。

　　 ——皮埃尔·西蒙·拉普拉斯，《关于概率的哲学论文》[72]

　　 这个智慧通常被称为拉普拉斯的魔鬼（与麦克斯韦的魔鬼类似），有时也叫做拉普拉斯的超人（根据汉斯·赖兴巴赫的说法）。拉普拉斯本人并没有使用‘魔鬼’一词，这是后来的附加。正如上文所翻译的那样，他仅仅提到：‘Une intelligence ... Rien ne serait incertain pour elle, et l’avenir comme le passé, serait présent à ses yeux.’（一种智慧……对她来说，什么都不不确定，未来和过去对她来说是一样的。）"

　　 尽管拉普拉斯通常被认为是首次提出因果决定论概念的人，但在哲学语境中，这一思想在当时实际上是广泛存在的，早在 1756 年，莫培尔图斯的《关于占卜》一书中就可以找到类似的观点。[73] 此外，耶稣会科学家博斯科维奇在他 1758 年的著作《自然哲学理论》中，也首次提出了与拉普拉斯的科学决定论非常相似的版本。[74]

10. 拉普拉斯变换

　　 早在 1744 年，欧拉就开始寻求微分方程的解，并且拉格朗日也跟随其后，试图寻找以下形式的解：[75] \[ z = \int X(x) e^{ax} \, dx \quad \text{和} \quad z = \int X(x) x^a \, dx. ~\] 拉普拉斯变换的形式为： \[ F(s) = \int f(t) e^{-st} \, dt~ \] 这个积分算子将一个时间函数（\( t \)）转换为一个复变数函数（\( s \)），通常将 \( s \) 解释为复频率。

11. 其他发现和成就

数学

　　 拉普拉斯在纯数学和应用数学方面的其他发现和成就包括：

• 与亚历山大-特奥菲尔·范德蒙德同时讨论了行列式的通用理论（1772 年）；[13]
• 证明了每一个奇数次方程至少有一个实数二次因子[需要澄清]；[13]
• 拉普拉斯的积分近似法；
• 求解二阶线性偏微分方程；[13]
• 他是第一个考虑混合差分方程中难题的人，并证明了一个一阶和二阶有限差分方程的解总是可以用连分数的形式表示；[6][13]
• 在他的概率论中：
• 德·莫夫-拉普拉斯定理，它用正态分布近似二项分布；
• 计算多个常见定积分；[13]
• 拉格朗日反演定理的一般证明。[13]

表面张力

　　 主条目：杨–拉普拉斯方程 § 历史 拉普拉斯在托马斯·杨的定性研究基础上，发展了毛细作用的理论和杨–拉普拉斯方程。

声速

　　 1816 年，拉普拉斯首次指出，空气中声速取决于热容量比。牛顿的原始理论给出的声速值过低，因为它没有考虑空气的绝热压缩，导致局部温度和压力的上升。拉普拉斯在实际物理学方面的研究主要局限于他与拉瓦锡于 1782 至 1784 年间共同进行的关于各种物体比热的研究。[13]

12. 政治

内政部长

　　 在早年，拉普拉斯小心谨慎，避免卷入政治，甚至不涉足科学院之外的生活。在革命最为暴力的时期，他明智地撤离了巴黎。[76]

　　 1799 年 11 月，在 18 日布鲁迈尔政变后，拿破仑立即任命拉普拉斯为内政部长。[6] 然而，这一任命仅持续了六周，随后拿破仑的兄弟卢西安·波拿巴接任了这一职位。[6] 显然，一旦拿破仑稳固了权力，就不再需要一位虽有声望但缺乏政府经验的科学家。[77] 拿破仑后来（在《圣赫勒拿回忆录》中）写道，关于拉普拉斯被解职的事情如下：[13]

　　 “作为一流的几何学家，拉普拉斯很快就表现出他是一个比平均水平还差的行政官员；从他上任后的第一步行动开始，我们就意识到这是一个错误。拉普拉斯没有从正确的角度看待任何问题：他到处寻求微妙的差异，只构思问题，最终把‘无穷小’的精神带入了行政管理中。”

　　 然而，格雷坦-吉尼斯（Grattan-Guinness）认为这些评论是 “带有倾向性的”，因为似乎毫无疑问，拉普拉斯 “只是被任命为短期的傀儡人物，是在拿破仑巩固权力的同时的一个替代者”。[77]

从波拿巴到波旁家族

　　 虽然拉普拉斯被免职，但保持他的忠诚度仍然是必要的。因此，他被提升为参议员，并在《天体力学》的第三卷前附上一段注释，表示对欧洲和平缔造者的忠诚是对作者来说最宝贵的真理。[6] 在波旁复辟后的售出版本中，这段话被删除。（皮尔逊指出，审查员无论如何也不会允许它。）1814 年时，帝国已经显现出崩溃的迹象；拉普拉斯急忙向波旁王朝表示效忠，并在 1817 年复辟期间因而被授予了侯爵头衔。

　　 根据罗斯·鲍尔的说法，他的许多诚实的同事对他的行为表示蔑视，这一点可以在保罗·路易·库里耶的作品中看到。拉普拉斯的知识在他参与的众多科学委员会中起到了重要作用，罗斯·鲍尔认为，这或许解释了为何他的政治虚伪行为得以被忽视。[13]

　　 在他 2005 年的传记中，罗杰·汉恩（Roger Hahn）质疑将拉普拉斯描绘成机会主义者和叛徒的说法，指出与法国许多人一样，拉普拉斯在看到拿破仑的俄罗斯远征失败后，产生了严重的怀疑。拉普拉斯一家，在他们唯一的女儿索菲于 1813 年 9 月因分娩去世后，深感忧虑，他们的儿子埃米尔正随帝王在东线作战。拿破仑最初上台时承诺带来稳定，但显然他已经过度扩张，国家因此陷入了危险。正是在这一时刻，拉普拉斯的忠诚开始动摇。尽管他仍然可以轻松接触到拿破仑，但他与皇帝的个人关系明显冷淡了许多。作为一个失去女儿的父亲，拉普拉斯对拿破仑的冷漠尤为感到伤痛，曾由让-安托万·夏普塔尔（Jean-Antoine Chaptal）讲述过一段对话：“从莱比锡的失败战场回来时，拿破仑走近拉普拉斯先生：‘哦，我看你瘦了——陛下，我失去了我的女儿——哦！这不是减肥的理由。你是个数学家，把这个事件写成方程式，你会发现它的结果是零。’”[78]

政治哲学

　　 在《哲学论文集》第二版（1814 年）中，拉普拉斯对政治和治理作出了一些揭示性的评论。他指出，因为 “正义、理性和人道的永恒原则在实践中创造并维持了社会，所以坚持这些原则具有巨大的优势，而偏离它们则是极其不明智的。”[79][80] 他提到，“当雄心勃勃的领导者无视这些原则时，人民会被投进深深的苦难”，并对拿破仑的行为进行了含蓄的批评：“每当一个伟大的强国因征服欲望而渴望实现普遍统治时，受到不公正威胁的民族间便会产生联盟，而这个联盟最终总会战败。” 拉普拉斯认为，“在引导和约束各国的多种因素之中，存在着‘自然的界限’，在这些界限之内，‘国家的稳定和帝国的繁荣是至关重要的’。越过这些界限的国家无法避免‘回归’这些界限，就像当海水的海床因暴风骤雨而被抬高时，海水最终会因重力作用恢复到原有水平。”[81][82]

　　 关于他所目睹的政治动荡，拉普拉斯基于物理学原理提出了一套原则，倾向于支持渐进变化而非革命性变革：

　　 “让我们将基于观察和计算的方法应用于政治和道德科学，这种方法在自然科学中已经为我们服务得如此成功。我们不应对来自启蒙进步的不可避免的好处作出无益且常常有害的抵抗；但我们应以极大的谨慎改变我们的制度和我们长时间以来所采用的习惯。我们从过去的经验中知道它们可能带来的弊端，但我们不知道变革可能带来的疾病的严重程度。面对这种无知，概率理论教导我们避免一切变化，尤其是避免突如其来的变革，因为在道德世界和物理世界中，突变从来不会没有显著的生命力损失。”[83]

　　 在这些话语中，拉普拉斯表达了他在经历了革命和帝国后所形成的观点。他认为，科学发现揭示的自然稳定性为最有助于保全人类物种的模式。“这些观点，” 哈恩评论道，“也与他坚定的个性相一致。”[82]

　　 在《哲学论文集》中，拉普拉斯还通过应用大数法则，展示了概率在政治研究中的潜力，以此为依据来为使用博尔达投票法选举新成员的科学学会成员的候选人整数排名提供正当性。拉普拉斯的语言论证如此严谨，以至于它可以轻易地转化为形式证明。[84][85]

13. 死亡

　　 拉普拉斯于 1827 年 3 月 5 日去世，恰逢亚历山德罗·伏打去世的同一天。他的大脑被他的医生弗朗索瓦·马让迪（François Magendie）取出，并保存了许多年，最终在英国的一个流动解剖学博物馆中展出。据说他的脑容量比平均水平要小。[8] 拉普拉斯被埋葬在巴黎的佩尔·拉谢兹公墓，但在 1888 年，他的遗体被迁移到法国诺曼底奥尔贝克区圣朱利安·德·梅洛克（Saint Julien de Mailloc）的家族庄园，并重新安葬。墓地位于俯瞰圣朱利安·德·梅洛克村的山丘上。

14. 宗教观点

我不需要那个假设

　　 一段常被引用但可能是杜撰的关于拉普拉斯与拿破仑的互动，涉及上帝的存在。虽然这段对话确实发生过，但拉普拉斯使用的确切语言及其意图并不为人所知。Rouse Ball 提供了一个典型版本：[13]

　　 拉普拉斯盛装前往拿破仑处，呈交他的大作，关于这次会面的叙述得到了广泛认证，并且如此符合所有相关人物的特点，以至于我将其完整引用。据说，有人告诉拿破仑，这本书中没有提到上帝的名字。拿破仑喜欢提出令人尴尬的问题，接过书时说：“拉普拉斯先生，他们告诉我你写了这本关于宇宙体系的大书，却从未提到它的创造者。” 拉普拉斯，虽然在政治上极为圆滑，但在哲学上却像烈士一样刚直，挺直身子直接回答道：“Je n'avais pas besoin de cette hypothèse-là.”（“我不需要那个假设。”）拿破仑大为逗乐，便将这个回答转告给拉格朗日，拉格朗日感叹道：“Ah! c'est une belle hypothèse; ça explique beaucoup de choses.”（“啊，那是一个很好的假设，它解释了许多事情。”）

　　 早期的报告中，尽管没有提到拉普拉斯的名字，但在安托马基的《拿破仑的最后时刻》（1825 年）中找到了类似的记载：[87]

　　 “我和 L.....交谈时，我祝贺他刚刚出版的一本书，并问他，为什么在拉格朗日的作品中，上帝的名字不断出现，而在他的书中却一次也没有提到。他回答说：‘因为我不需要那个假设。’”

　　 然而，在 1884 年，天文学家厄尔维·法耶（Hervé Faye）[88][89] 宣称，关于拉普拉斯与拿破仑的对话的这一记载，呈现了一个 “奇怪转变”（étrangement transformée）或歪曲的版本，实际上并非拉普拉斯所说的内容。他认为，拉普拉斯并不是将上帝视为假设，而是仅仅将上帝在某一确定时刻的干预视为假设：

　　 “事实上，拉普拉斯从未说过那句话。我认为，真正发生的事情是这样的：牛顿认为，他在理论中概述的世俗扰动最终会导致太阳系的毁灭，于是他曾在某个地方说过，上帝必须不时地干预，以解决问题并保持系统的正常运行。然而，这只是一个纯粹的假设，是牛顿因对我们小世界的稳定条件认识不完全而提出的。在当时，科学尚未发展到足以完全揭示这些条件的程度。但拉普拉斯通过深入分析发现了这些条件，他会对第一执政（拿破仑）回应，指出牛顿错误地提到上帝干预来不时调整世界的机器（la machine du monde），而他拉普拉斯则不需要这种假设。因此，拉普拉斯并不是将上帝视为假设，而是将其在某一时刻的干预作为假设。”

　　 拉普拉斯的年轻同事、天文学家弗朗索瓦·阿拉戈（François Arago），他在 1827 年为拉普拉斯做了悼词[90]，曾告诉法耶关于拉普拉斯试图阻止他与拿破仑的互动版本被传播的尝试。法耶写道：[88][89]

　　 “我从阿拉戈先生那里得知，拉普拉斯在临终前不久得知那段轶事即将被出版在一部传记合集里，他曾要求阿拉戈请求出版商删除这段内容。必须要么解释它，要么删除，而删除显然是更为简便的方式。但不幸的是，这段内容既没有被删除，也没有被解释。”

　　 瑞士裔美国数学史学者弗洛里安·卡乔里（Florian Cajori）似乎并不知道法耶的研究，但在 1893 年他得出了类似的结论。[91] 斯蒂芬·霍金在 1999 年曾表示[71]：“我不认为拉普拉斯声称上帝不存在。只是他说上帝并不干预，不会违反科学的法则。”

　　 拉普拉斯与拿破仑互动的唯一目击记载来自英国天文学家威廉·赫歇尔爵士的 1802 年 8 月 8 日的日记条目：[92]

　　 “第一执政接着问了一些关于天文学和天体构造的问题，我的回答似乎令他非常满意。他还就同一主题向拉普拉斯先生请教，并与他展开了一场相当激烈的争论，在这场争论中他与这位杰出的数学家意见不合。分歧源于第一执政的一个感叹，他在我们讨论星际天体的广袤时，带着惊叹或钦佩的语气问道：‘这一切的作者是谁！’拉普拉斯先生试图说明，自然原因的链条可以解释这个奇妙系统的构造和维持。然而，第一执政对此表示反对。关于这个话题可以有很多话要说；通过结合两者的论点，我们最终会得出‘自然与自然之神’。”

　　 由于这段记载没有提到拉普拉斯说过 “我不需要这个假设” 这样的言论，丹尼尔·约翰逊[93]认为 “拉普拉斯从未说过那些被归于他的话。” 然而，阿拉戈的证词似乎暗示拉普拉斯确实说过，只是并非指上帝的存在。

拉普拉斯的宗教观点

　　 拉普拉斯在天主教家庭中长大，成年后似乎倾向于自然神论（这可能是他深思熟虑后的立场，因为这是他著作中唯一出现的立场）。然而，他的部分同时代人认为他是无神论者，而一些近期学者则将他描述为不可知论者。

　　 费耶认为拉普拉斯 “并不宣扬无神论”[88]，但拿破仑在圣赫勒拿岛时曾告诉加斯帕·古尔戈将军：“我常问拉普拉斯他如何看待上帝。他承认自己是无神论者。”[94] 罗杰·哈恩在他的拉普拉斯传记中提到一次晚宴，地质学家让-埃蒂安·盖塔尔对拉普拉斯大胆否定上帝存在的言论感到震惊。盖塔尔认为拉普拉斯的无神论 “是建立在彻底的唯物主义之上的”[95]。但化学家让-巴普蒂斯特·杜马斯，曾在 1820 年代与拉普拉斯相识，他写道，拉普拉斯 “为唯物主义者提供了看似有理的论据，但并不认同他们的信念”[96][97]。

　　 哈恩指出：“在他的公开和私人著作中，拉普拉斯从未否认上帝的存在。”[98] 他的私人信件中有一些表达，似乎与无神论不一致。[6] 例如，在 1809 年 6 月 17 日，他写信给儿子：“Je prie Dieu qu'il veille sur tes jours. Aie-Le toujours présent à ta pensée, ainsi que ton père et ta mère [我祈求上帝保佑你的日子。愿他永远在你的心中，正如你的父亲和母亲一样]。”[89][99] 伊恩·S·格拉斯引用赫歇尔关于与拿破仑著名对话的记载，写道拉普拉斯 “显然是像赫歇尔一样的自然神论者。”[100]

　　 在《世界体系的阐述》中，拉普拉斯引用了牛顿的断言：“太阳、行星和彗星的奇妙安排，只有全能且智能的存在才能完成。”[101] 拉普拉斯表示，这一思想 “如果牛顿知道我们所展示的事实，他会更加坚定，那个事实即行星及其卫星的排列条件正是确保其稳定性的条件。”[102] 通过证明行星的 “显著” 排列可以完全通过运动定律来解释，拉普拉斯消除了 “至高无上的智慧” 介入的需要，正如牛顿曾 “让” 它那样。[103] 拉普拉斯赞同莱布尼茨对牛顿求助于神力恢复太阳系秩序的批评：“这显示了对上帝的智慧和力量的狭隘看法。”[104] 他显然和莱布尼茨一样，对牛顿的信念感到惊讶，即 “上帝把他的机器做得如此糟糕，除非通过某种特殊手段干预，否则时钟很快就会停摆。”[105]

　　 在一组手稿中，这些手稿被相对保密地保存在一个黑色信封中，存放在法国科学院的图书馆里，并由哈恩首次发表，拉普拉斯提出了对基督教的自然神论批评。他写道，拒绝奇迹事实作为不真实的是 “第一条且最无误的原则”。[106] 至于化体说的教义，它 “同时冒犯了理性、经验、我们所有感官的证据、自然的永恒法则，以及我们应该对至高存在形成的崇高观念”。认为 “宇宙的至高立法者会暂停他所建立的法则，并且这些法则似乎一直不变地得到维持”，简直是荒谬至极。[107]

　　 拉普拉斯还嘲笑了概率在神学中的运用。即使按照帕斯卡的推理，即帕斯卡赌注的思想，这样的赌注也不值得下，因为盈利的希望——等于证词的价值（无穷小）和它们承诺的幸福价值（虽然显著但有限）的乘积——必然是无穷小的。[108]

　　 晚年，拉普拉斯依然对上帝的问题保持好奇[109]，并且经常与瑞士天文学家让-弗雷德里克-西奥多·莫里斯讨论基督教[110]。他告诉莫里斯，“基督教是一件非常美好的事情”，并赞扬其文明影响。莫里斯认为拉普拉斯的信仰基础正一点一点发生变化，但他依然坚持认为自然法则的恒定性不容许超自然事件的发生。[109] 拉普拉斯去世后，泊松告诉莫里斯：“你知道我不赞同你的[宗教]观点，但我的良心迫使我说出一件事，这一定会让你高兴。” 当泊松称赞拉普拉斯的 “辉煌发现” 时，垂死的拉普拉斯用沉思的目光注视着他并回答道：“啊！我们在追逐幻影[chimères]。”[111] 这些是他临终的遗言，被莫里斯解读为他对尘世追求最终 “虚荣” 的觉悟。[112] 拉普拉斯接受了外国传教士教区的神父（他将在此教区埋葬）[97] 和阿尔克耶的神父[112]的最后圣事。

　　 根据他的传记作者罗杰·哈恩的说法，“拉普拉斯有一个合格的天主教式死亡” 是不可信的，他 “始终保持怀疑态度”，直到生命的最后一刻。[113] 拉普拉斯在他生命的最后几年被描述为不可知论者。[114][115][116]

彗星的逐出教门

　　 在人文主义学者巴尔托洛梅奥·普拉提纳（Bartolomeo Platina）于 1470 年所写的《教皇历》中，曾提到教皇卡里斯特三世在 1456 年哈雷彗星出现时，曾请求为从土耳其人手中拯救祈祷。[117] 然而，普拉提纳的记载与教会的档案并不一致，教会的记录中并未提及彗星。拉普拉斯据称曾夸大其词，声称教皇 “逐出了” 哈雷彗星。[118] 但拉普拉斯在《世界体系的阐述》（1796 年）中实际说的是，教皇曾命令对彗星进行 “驱魔”（conjuré）。是阿拉戈（Arago）在《彗星通论》（1832 年）中首次提到 “逐出教门” 一词。[119][120][121]

15. 荣誉

• 1809 年，成为荷兰皇家学会的通讯会员。[122]
• 1822 年，成为美国艺术与科学学院的外籍荣誉会员。[123]
• 小行星 4628 号以拉普拉斯命名。[124]
• 月球上的蒙特斯·朱拉山脉（Montes Jura）一处山脊被称为拉普拉斯岬（Promontorium Laplace）。
• 拉普拉斯的名字是埃菲尔铁塔上 72 个名字之一。
• 欧洲空间局的欧罗巴木星系统任务的暂定工作名称为 “拉普拉斯” 空间探测器。
• 阿尔库伊尔（Arcueil）RER B 线的一个火车站以他的名字命名。
• 俄罗斯罗斯托夫州的维尔赫内泰梅尔尼茨基（Verkhnetemernitsky）一条街道以他的名字命名。
• 电气与电子工程师协会（IEEE）信号处理学会的早期职业技术成就奖以他命名。[125]

16. 名言

• "我不需要这个假设。"（“Je n'avais pas besoin de cette hypothèse-là”，据称这是他对拿破仑的回答，拿破仑问他为什么在关于天文学的书中没有提到上帝。）[13]
• "因此显而易见的是..."（在《天体力学》中经常使用，当他证明了某个东西但找不到证明或认为证明很笨拙时。作为信号，表示某个东西是真实的，但难以证明。）
• "如果我们在每个对称现象中寻找原因，并不是因为我们认为对称事件比其他事件更不可能，而是因为这个事件应该是规律性原因的结果，或者是偶然的结果，第一种假设比第二种更为可能。" [126]
• "事件越是非凡，越需要强有力的证据来支撑它。" [127]
• "我们距离了解所有自然界的作用因素及其多样的作用方式还有很远，因此，仅仅因为现有知识无法解释某些现象，就否定它们是不符合哲学的。但我们应该以更加谨慎的态度来考察它们，特别是当承认这些现象显得更加困难时。" [128]
• 这在西奥多·弗洛诺瓦（Theodore Flournoy）的著作《从印度到火星》（From India to the Planet Mars）中被重新表述为拉普拉斯原理或 “证据的分量应该与事实的奇异性成比例。” [129]
• 最常重复的说法是：“对一个非凡主张的证据重量必须与其奇异性成比例。”（另见：萨根标准）
• "如果我们考虑到大自然的所有效果仅仅是少数不变法则的数学结果，这种比率的简洁性就不会令人惊讶。" [130]
• "大自然的效果是无穷多样的，但她的原因却是简单的。" [131]
• "我们所知道的很少，而我们所不知道的却是无穷的。"（傅立叶评论：“这至少是他最后的话的意思，尽管他说话时非常艰难。”）[66]
• "在这篇文章中可以看出，概率论基本上只是将常识转化为一种计算方法。它让人准确估计出那些有理智的人通过某种直觉感受到的东西，通常无法给出理由。" [132]

17. 著作列表

• 《天体力学教程》（法文）。第一卷。巴黎：查尔斯·克拉普莱（Charles Crapelet）。1799 年。
• 《天体力学教程》（法文）。第二卷。巴黎：查尔斯·克拉普莱（Charles Crapelet）。1799 年。
• 《天体力学教程》（法文）。第三卷。巴黎：查尔斯·克拉普莱（Charles Crapelet）。1802 年。
• 《天体力学教程》（法文）。第四卷。巴黎：查尔斯·克拉普莱（Charles Crapelet）。1805 年。
• 《天体力学教程》（法文）。第五卷。巴黎：查尔斯·路易·埃蒂安·巴谢利耶（Charles Louis Étienne Bachelier）。1852 年。
• 《天文学历史概要》（意大利文）。米兰：安吉洛·斯坦尼斯劳·布兰比拉（Angelo Stanislao Brambilla）。1823 年。
• 《世界体系的阐述》（法文）。巴黎：查尔斯·路易·埃蒂安·巴谢利耶（Charles Louis Étienne Bachelier）。1824 年。

18. 参考书目

• 《拉普拉斯全集》，14 卷（1878–1912），巴黎：高蒂耶-维拉尔（法文版来自 Gallica）
• 《行星的运动与椭圆形状理论》（1784），巴黎（未收入《拉普拉斯全集》）
• 《天文学历史概要》
• 阿尔方斯·雷比埃尔，《数学与数学家》，第三版，巴黎：诺尼与公司，1898 年

英文翻译

• Bowditch, N.（译）（1829–1839）《天体力学》，4 卷，本顿
• 重版版本，由 Reprint Services 出版，ISBN 0-7812-2022-X
• – [1829–1839]（1966–1969）《天体力学》，5 卷，包括原版法文
• Pound, J.（译）（1809）《世界体系》，2 卷，伦敦：理查德·菲利普斯
• _《世界体系》（第 1 卷）
• _《世界体系》（第 2 卷）
• – [1809]（2007）《世界体系》第 1 卷，凯辛格，ISBN 1-4326-5367-9
• Toplis, J.（译）（1814）《解析力学教程》，诺丁汉：H. Barnett
• Laplace, Pierre Simon Marquis De（2007）[1902]《概率哲学论文集》，由 Truscott, F.W.和 Emory, F.L.翻译，Cosimo 出版社，ISBN 978-1-60206-328-0，翻译自法文第 6 版（1840 年）
• 《概率哲学论文集》（1902 年）见互联网档案馆
• Dale, Andrew I.; Laplace, Pierre-Simon（1995）。《概率哲学论文集》，数学和物理科学历史中的源材料，第 13 卷，Andrew I. Dale 翻译，Springer，doi:10.1007/978-1-4612-4184-3，hdl:2027/coo1.ark:/13960/t3126f008，ISBN 978-1-4612-8689-9，翻译自法文第 5 版（1825 年）

19. 参见

• 米的历史
• 拉普拉斯–贝叶斯估计量
• 比率估计量
• 秒摆
• 以皮埃尔-西蒙·拉普拉斯命名的事物列表
• 帕斯卡的赌注

20. 参考文献

引用

1. S.W. 霍金与乔治·F.R. 埃利斯，《时空的大尺度结构》，剑桥大学出版社，1973 年，第 364 页。
2. 福里斯特，托马斯（2018 年 3 月 28 日）。《皮埃尔-西蒙·拉普拉斯生日快乐》。COMSOL。检索日期：2024 年 12 月 4 日。
3. 斯蒂格勒，斯蒂芬·M.（1986 年）。《统计学的历史：1900 年前的不确定性测量》。哈佛大学出版社，第 3 章。
4. 蒙哥马利，科林；奥奇斯顿，韦恩；惠廷厄姆，伊恩（2009 年）。《米歇尔、拉普拉斯与黑洞概念的起源》。天文历史与遗产杂志，12（2）：90-96。doi:10.3724/SP.J.1440-2807.2009.02.01。ISSN 1440-2807。S2CID 55890996。
5. 芬恩，伯纳德·S.（1964 年）。《拉普拉斯与音速》。《艾西斯》，55（1）：7-19。doi:10.1086/349791。ISSN 0021-1753。
6. 克勒克，阿格尼斯·玛丽（1911 年）。《皮埃尔·西蒙·拉普拉斯》。大英百科全书，第 16 卷（第 11 版）。第 200-202 页。
7. 汉金斯，托马斯·L.（2006 年）。《皮埃尔·西蒙·拉普拉斯，1749-1827：一位坚毅的科学家（书评）》。物理学今日，59（9）：62-64。doi:10.1063/1.2364251。
8. 《拉普拉斯，摘自卡尔·皮尔逊的讲座》，《生物统计学》，第 21 卷，1929 年 12 月，第 202-216 页。
9. W.W. Rouse Ball，《数学史简述》，第 4 版，1908 年。
10. *O'Connor, John J.; Robertson, Edmund F.，《皮埃尔-西蒙·拉普拉斯》，MacTutor 数学历史档案，圣安德鲁斯大学。检索日期：2007 年 8 月 25 日。
11. 惠蒂克，爱德蒙（1949 年）。《拉普拉斯》。数学公报，33（303）：1-12。doi:10.2307/3608408。JSTOR 3608408。
12. 吉利斯皮（1997 年），第 3-4 页。
13. Rouse Ball（1908 年）。
14. “安托万-洛朗·拉瓦锡的化学革命国际历史化学地标”。美国化学学会。1999 年 6 月 8 日。
15. 戈林斯基，简·V.（1983 年 6 月）。“安托万·洛朗·拉瓦锡、皮埃尔·西蒙·拉普拉斯、亨利·格尔拉克”。艾西斯，74（2）：288-289。doi:10.1086/353288。
16. 吉利斯皮（1997 年），第 5 页。
17. “科学界对拉普拉斯的影响” 检索日期：2018 年 1 月 10 日。
18. 哈恩（2005 年），第 99 页。然而，吉利斯皮（1997 年），第 67 页，给出了结婚月份为 5 月。
19. 哈恩（2005 年），第 99-100 页。
20. 吉利斯皮（1997 年），第 67 页
21. 哈恩（2005 年），第 101 页
22. 吉利斯皮（1989 年），第 7-12 页
23. 吉利斯皮（1989 年），第 14-15 页
24. 惠特罗（2001 年）
25. 切莱蒂，A. 和 佩罗齐，E.（2007 年）。《天体力学：行星的华尔兹》。柏林，德国：Springer。Bibcode:2006cmwp.book.....C。ISBN 978-0-387-30777-0。
26. 惠蒂克（1949b）
27. 吉利斯皮（1997 年），第 29-35 页
28. 吉利斯皮（1997 年），第 35-36 页
29. “拉普拉斯”。传记。数学与统计学系。圣安德鲁斯，苏格兰：圣安德鲁斯大学。
30. “拉普拉斯的动力学理论简要笔记”。2011 年 11 月 20 日。原文已于 2015 年 4 月 2 日归档。检索日期：2017 年 10 月 28 日。
31. 豪塔拉，苏珊；凯利，凯瑟琳；汤普森，卢安（2005 年）。《潮汐动力学》（PDF）。
32. 《高等教育》（PDF）。
33. 安，京珍（2009 年 9 月）。“天文学家对当前大学教材中潮汐描述的看法”（PDF）。韩国地球科学学会。
34. 潮汐理论，已于 2017 年 8 月 22 日在 “Wayback Machine” 网站归档，南非海军水文办公室。
35. “潮汐的动态理论”。Oberlin.edu。检索于 2012 年 6 月 2 日。
36. “潮汐的动态理论”。
37. “动态潮汐——与‘静态’理论相对，潮汐的动态理论认为水面只覆盖三分之四。” Web.vims.edu。原文已于 2013 年 1 月 13 日归档。检索于 2012 年 6 月 2 日。
38. “潮汐的动态理论”。Coa.edu。原文已于 2013 年 12 月 19 日归档。检索于 2012 年 6 月 2 日。
39. “潮汐”。beacon.salemstate.edu。原文已于 2012 年 12 月 14 日归档。检索于 2022 年 2 月 3 日。
40. “潮汐——建筑、河流、海洋、深度、海洋、效应、重要、最大、系统、波、效应、海洋、太平洋”。Waterencyclopedia.com。2010 年 6 月 27 日。
41. “潮汐”。Ocean.tamu.edu。原文已于 2013 年 6 月 16 日归档。检索于 2012 年 6 月 2 日。 Floor Anthoni。
42. “潮汐”。Seafriends.org.nz。检索于 2012 年 6 月 2 日。
43. “潮汐的原因与性质”。
44. “科学可视化工作室 TOPEX/Poseidon 图像”。Svs.gsfc.nasa.gov。检索于 2012 年 6 月 2 日。
45. “TOPEX/Poseidon 西半球：潮汐高度模型：NASA/戈达德航天中心科学可视化工作室：免费下载与流媒体：互联网档案馆”。2000 年 6 月 15 日。
46. TOPEX 数据用于建模 2000 年实际潮汐，时长 15 天。TOPEX/Poseidon 平面地球潮汐高度模型，已于 2015 年 9 月 18 日通过 Wayback Machine 归档。
47. http://www.geomag.us/info/Ocean/m2_CHAMP+longwave_SSH.swf [永久失效链接]
48. “OSU 潮汐数据反演”。Volkov.oce.orst.edu。原文已于 2012 年 10 月 22 日归档。检索于 2012 年 6 月 2 日。
49. “为改进 GRACE 去别名化（DAROTA）进行的动态与残余海洋潮汐分析”。已于 2015 年 4 月 2 日归档。
50. “拉普拉斯潮汐方程和大气潮汐”（PDF）。原文（PDF）已于 2019 年 4 月 11 日归档。检索于 2017 年 10 月 28 日。
51. Grattan-Guinness, I.（2003 年）。《数学科学的历史与哲学伴随百科全书》。巴尔的摩：约翰·霍普金斯大学出版社。第 1097-1098 页。ISBN 978-0-8018-7396-6。
52. W.W. Rouse Ball，《数学史简短概述》（第四版，1908 年）
53. Green, G.（1828）。《数学分析在电学和磁学理论中的应用论文》。诺丁汉。arXiv:0807.0088。Bibcode:2008arXiv0807.0088G。
54. Kline, Morris（1972）。《从古代到现代的数学思维》。第 2 卷。牛津大学出版社，第 524–525 页。ISBN 978-0-19-506136-9。
55. Euler, Leonhard（1757）。《流体运动的通用原理》。Novi. Comm. Acad. Sci. Petrop.：271–311。
56. Maxwell, James（1881）。《电学与磁学论》。第 29 页（PDF）。
57. Arago, François（1874）。《拉普拉斯：颂词》。由 Baden Powell 翻译。史密森学会，第 5 页。检索于 2018 年 3 月 21 日。
58. Owen, T. C.（2001）。《太阳系：太阳系的起源》，《大英百科全书》，豪华 CD-ROM 版。
59. Fox, Robert（1974）。《拉普拉斯物理学的兴衰》。物理科学历史研究，4：89–136。doi:10.2307/27757328。ISSN 0073-2672。JSTOR 27757328。
60. Darrigol, Olivier（2012 年 1 月 26 日）。《从古希腊到十九世纪的光学史》。牛津大学出版社。ISBN 978-0-19-162745-3。
61. Whittaker, E. T. (1989). 《以太与电的理论史》。纽约：多佛出版公司。ISBN 978-0-486-26126-3。
62. Laplace, P.-S. (1799). 《一般地理年鉴》由 F. von Zach 编纂。第四卷，第一部分，第一篇文章，魏玛；英文翻译：Hawking, Stephen W.; Ellis, George F.R. (1973). 《时空的大尺度结构》。剑桥大学出版社，第 365 页及以后。ISBN 978-0-521-09906-6。
63. Colin Montgomery, Wayne Orchiston 和 Ian Whittingham, "Michell, Laplace 和黑洞概念的起源"（2009 年）。《天文学历史与遗产期刊》，12(2)，90–96。2021 年 6 月 18 日从 Wayback Machine 存档。
64. 参见 Israel（1987 年），第 7.2 节。
65. Gribbin, 299。
66. Fourier（1829）。
67. Crosland（1967），第 1 页。
68. Stigler（1975）。
69. "Laplace, Pierre-Simon Marquis de – 《数学百科全书》"。来自 encyclopediaofmath.org。检索于 2021 年 6 月 18 日。
70. Laplace, Pierre Simon，《概率哲学论文》，由 Frederick Wilson Truscott 和 Frederick Lincoln Emory 翻译自第六版法文版。纽约：John Wiley & Sons，1902 年，第 19 页。Dover 出版公司版（1951 年纽约）具有相同的页码。
71. Hawking, Stephen (1999). "上帝掷骰子吗？" 公开讲座。原文已于 2000 年 7 月 8 日存档。
72. Laplace，《概率哲学论文》，纽约，1902 年，第 4 页。
73. van Strien, Marij (2014). "关于拉普拉斯决定论的起源和基础"。《科学史与哲学研究》45: 24–31。Bibcode:2014SHPSA..45...24V. doi:10.1016/j.shpsa.2013.12.003。PMID 24984446。S2CID 19302364。检索于 2021 年 2 月 5 日。
74. Cercignani, Carlo (1998). "第二章：玻尔兹曼之前的物理学"。Ludwig Boltzmann, 《信任原子的男人》。牛津大学出版社，第 55 页。ISBN 978-0-19-850154-1。
75. Grattan-Guinness, in Gillispie (1997)，第 260 页。
76. Crosland (2006)，第 30 页。
77. Grattan-Guinness (2005)，第 333 页。
78. Hahn (2005)，第 191 页。
79. Laplace，《概率哲学论文》，纽约，1902 年，第 62 页。（本文段的翻译来自 Hahn。）
80. Hahn (2005)，第 184 页。
81. Laplace，《概率哲学论文》，纽约，1902 年，第 63 页。（本文段的翻译来自 Hahn。）
82. Hahn (2005)，第 185 页。
83. Laplace，《概率哲学论文》，纽约，1902 年，第 107-108 页。（本文段的翻译来自 Hahn。）
84. Black, Duncan (1987) [1958]。《委员会与选举理论》。Springer 科学与商业媒体。ISBN 978-0-89838-189-4。
85. Tangian, Andranik (2020)。《民主的分析理论》第一卷与第二卷。《选择与福利研究》。瑞士查姆：Springer 出版社，第 132 页起。doi:10.1007/978-3-030-39691-6。ISBN 978-3-030-39690-9。S2CID 216190330。
86. Gillispie (1997)，第 278 页。
87. 第 282 页，《医生 F.安托马奇的回忆，或拿破仑的最后时光》，第一卷，1825 年，巴黎：Barrois L'Ainé。
88. Faye, Hervé (1884)，《世界的起源：古代与现代的宇宙生殖理论》。巴黎：Gauthier-Villars，第 109–111 页。
89. Pasquier, Ernest (1898)。《宇宙生殖假说（续）》。《新斯多卡学派回顾》，第 50 年，第 18 期，第 124–125 页，脚注 1。
90. Arago, François (1827)，《拉普拉斯：法国科学院的悼词》，由 Baden Powell 教授翻译，史密森报告，1874 年。
91. Cajori, Florian (1893)，《数学史》。第五版（1991 年），由美国数学学会于 1999 年再版，第 262 页。ISBN 0-8218-2102-4。
92. William Herschel 的巴黎旅行日记，引用自《赫歇尔年鉴》第 310 页，Constance A. Lubbock，剑桥：剑桥大学出版社，2013 年，ISBN 1-107-65001-1。
93. Johnson, Daniel (2007 年 6 月 18 日)，《假设的无神论者》，评论。
94. 《拿破仑在圣赫勒拿岛的谈话》，由 Elizabeth Wormely Latimer 翻译，芝加哥：A.C. McClurg & Co.，1903 年，第 276 页。
95. Hahn (2005)，第 67 页。
96. Dumas, Jean-Baptiste (1885)，《学术演讲与悼词》，第二卷。巴黎：Gauthier-Villars，第 255 页。
97. Kneller, Karl Alois，《基督教与现代科学的领袖：19 世纪文化史的贡献》，由 T.M. Kettle 翻译自第二版德文版。伦敦：B. Herder，1911 年，第 73–74 页。
98. Hahn (1981)，第 95 页。
99. 《拉普拉斯全集》。巴黎：Gauthier-Villars，1878 年，第一卷，第 v–vi 页。
100. Glass, Ian S. (2006)，《宇宙革命者：天体物理学家》。剑桥大学出版社，第 108 页。ISBN 0-19-857099-6。
101. 《自然哲学的数学原理》三卷书的《通用学说》，首次出现在第二版，1713 年。
102. Laplace，《世界体系的阐述》，第 6 版。布鲁塞尔，1827 年，第 522–523 页。
103. Laplace，《世界体系的阐述》，1827 年，第 523 页。
104. Leibniz 致 Conti 的信，1715 年 11 月或 12 月，见 H.G. Alexander 主编，《莱布尼茨–克拉克通信录》（曼彻斯特大学出版社，1956 年），附录 B，第 1 卷：“莱布尼茨与牛顿致 Conti 的信”，第 185 页，ISBN 0-7190-0669-4；引自 Laplace，《世界体系的阐述》，1827 年，第 524 页。
105. Leibniz 致 Conti 的信，1715 年，见 Alexander 主编，1956 年，第 185 页。
106. Hahn (2005)，第 220 页。
107. Hahn (2005)，第 223 页。
108. Jacques Attali (2004)，《帕斯卡尔》，华沙，第 368 页。
109. Hahn (2005)，第 202 页。
110. Hahn (2005)，第 202、233 页。
111. De Morgan, Augustus (1872)，《悖论集》，Longmans, Green and Co.，伦敦，第 3 页。比较埃德蒙·伯克因议员候选人突然去世而作出的名言：“我们是何等的影像，我们追逐的是何等的影像。”
112. Hahn (2005)，第 204 页。
113. Roger Hahn (2005)，《皮埃尔·西蒙·拉普拉斯，1749–1827：一位坚定的科学家》。哈佛大学出版社，第 204 页。ISBN 978-0-674-01892-1。天主教报纸《每日报》（La Quotidienne）宣布拉普拉斯死于两位神父的怀抱中，暗示他有一个合乎天主教教义的结局，但这并不可信。直到最后，他仍然是一个怀疑主义者，坚信自己的决定论信条，并保持从其丰富科学经验中派生出的不妥协的道德观。
114. Roger Hahn (2005)，《皮埃尔·西蒙·拉普拉斯，1749–1827：一位坚定的科学家》。哈佛大学出版社，第 202 页。ISBN 978-0-674-01892-1。公开场合，拉普拉斯保持着他的不可知论信仰，甚至在他年老时，仍然对上帝在决定论宇宙中可能扮演的角色持怀疑态度。
115. Morris Kline (1986)，《数学与知识的探索》。牛津大学出版社，第 214 页。ISBN 978-0-19-504230-6。拉格朗日和拉普拉斯，尽管出身于天主教家庭，却是不可知论者。
116. Edward Kasner；James Newman；James Roy Newman (2001)，《数学与想象力》。Courier Dover 出版社，第 253 页。ISBN 978-0-486-41703-5。现代物理学，事实上所有现代科学，像拉格朗日一样谦逊，像拉普拉斯一样不可知。
117. E. Emerson (1910)，《彗星传说》。Schilling 出版社，纽约，第 83 页。
118. C.M. Botley (1971)。《哈雷彗星 1456 年的传说》。天文台，第 91 卷，第 125-126 页。Bibcode:1971Obs....91..125B。
119. Hagen, John G. (1910)。《皮埃尔-西蒙·拉普拉斯》。见 Herbermann, Charles (编)。《天主教百科全书》第 8 卷。纽约：Robert Appleton 公司。
120. Stein, John (1911)。《巴尔托洛梅奥·普拉蒂纳》。见 Herbermann, Charles (编)。《天主教百科全书》第 12 卷。纽约：Robert Appleton 公司。
121. Rigge, William F. (1910 年 4 月)。《关于卡利斯图斯三世与哈雷彗星的历史考察》，《流行天文学》，第 18 卷，第 214-219 页。
122. "P.S. de Laplace (1749–1827)"。荷兰皇家艺术与科学学院。2015 年 7 月 19 日检索。
123. 《会员名册，1780-2010：L 章》（PDF）。美国艺术与科学院。2014 年 7 月 28 日检索。
124. Schmadel, L.D. (2003)。《小行星命名词典》（第五版修订版）。柏林：Springer-Verlag 出版社。ISBN 978-3-540-00238-3。
125. [https://signalprocessingsociety.org/sites/default/files/uploads/community_involvement/awards/Early_Career_Technical_Achievement_Award.pdf](https://signalprocessingsociety.org/sites/default/files/uploads/community_involvement/awards/Early_Career_Technical_Achievement_Award.pdf)
126. Laplace，《概率的哲学论文》，纽约，1902，第 16 页。
127. Laplace，《概率的哲学论文》，纽约，1902，第 17 页。
128. Laplace, Pierre Simon (1814)。“概率的哲学论文”。《自然》。110 (2748): 50。Bibcode:1922Natur.110....6B。doi:10.1038/110006b0。S2CID 4099834。
129. Flournoy, Théodore (1899)。《从印度到火星：关于一个带有语言现象的梦游案例的研究》。Slatkine。第 344-345 页。ISBN 978-2-05-100499-2。 Flournoy, Théodore (2007)。《从印度到火星：梦游案例研究》。Daniel D. Vermilye, 译。Cosimo, Inc. 第 369-370 页。ISBN 978-1-60206-357-0。
130. Laplace，《概率的哲学论文》，纽约，1902，第 177 页。
131. Laplace，《世界体系》，都柏林，1830，第 91 页。
132. Miller, Joshua B; Gelman, Andrew。“拉普拉斯的认知幻觉、启发式和偏差理论”（PDF）。哥伦比亚大学。未出版。2021 年 1 月 17 日检索。

一般来源

• Andoyer, H. (1922)。“拉普拉斯的科学工作”。巴黎（法文）。巴黎 Payot。
• Bibcode:1922osdl.book.....A。 Bigourdan, G. (1931)。“拉普拉斯的青年时期”。《现代科学》（法文）。9: 377-384。
• Crosland, M. (1967)。*《阿尔克伊尔学会：拿破仑时代的法国科学概览》*。剑桥，马萨诸塞州：哈佛大学出版社。ISBN 978-0-435-54201-6。
• – (2006) “拿破仑时代法国的科学帝国”，《科学史》，第 44 卷，第 29-48 页。
• Dale, A. I. (1982)。“贝叶斯还是拉普拉斯？贝叶斯定理的起源和早期应用的考察”。《精确科学史档案》。27: 23-47。doi:10.1007/BF00348352。S2CID 116147039。
• David, F. N. (1965) “关于拉普拉斯的一些笔记”，收录于 Neyman, J. & LeCam, L. M.（主编）《伯努利、贝叶斯与拉普拉斯》，柏林，第 30-44 页。
• Deakin, M. A. B. (1981)。“拉普拉斯变换的发展”。《精确科学史档案》。25 (4): 343-390。doi:10.1007/BF01395660。S2CID 117913073。
• Deakin, Michael A. B. (1982)。“拉普拉斯变换的发展，1737-1937 II. 从庞加莱到多茨，1880-1937”。《精确科学史档案》。26 (4)。Springer 科学与商业媒体公司：351-381。doi:10.1007/bf00418754。ISSN 0003-9519。S2CID 123071842。
• Dhombres, J. (1989)。“拉普拉斯的毛细现象理论：表面化的数学化还是扩展的数学化”。《科学历史与其应用杂志》（法文）。62: 43-70。doi:10.3406/rhs.1989.4134。
• Duveen, D. & Hahn, R. (1957)。“拉普拉斯继承贝祖的炮兵学员考官职位”。《伊西斯》。48 (4): 416-427。doi:10.1086/348608。S2CID 143451316。
• Finn, B. S. (1964). "拉普拉斯与声音的传播速度"。*伊西斯*。55: 7–19。doi:10.1086/349791。S2CID 20127770。
• Fourier, J. B. J. (1829)。"拉普拉斯侯爵的历史赞辞"（PDF）。*皇家科学学会会刊*（法文）。10: lxxxi–cii。2013 年 7 月 24 日归档。于 1829 年 6 月 15 日发表，1831 年出版。
• Gillispie, C. C. (1972)。"概率与政治：拉普拉斯、孔多塞与图尔戈"。*美国哲学学会学报*。116 (1): 1–20。
• Gillispie, Charles (1997)。*皮埃尔-西蒙·拉普拉斯：精确科学的生命*。普林斯顿，新泽西州：普林斯顿大学出版社。ISBN 0-691-01185-0。OCLC 36656386。
• Grattan-Guinness, I. (2005)。“*Exposition du système du monde* 和 *Traité de mécanique céleste*” 收录于他的著作《西方数学的里程碑写作》中。Elsevier：242–257。
• Gribbin, John. *科学家：通过伟大发明家的生活讲述科学的历史*。纽约：兰登书屋，2002 年，第 299 页。
• Hahn, R. (1955)。"拉普拉斯的宗教观点"。*国际科学历史档案*。8: 38–40。
• – (1981) "拉普拉斯与神在物理宇宙中消失的角色"，收录于 Woolf, Henry（主编），*分析精神：科学史论文集*。伊萨卡，纽约：康奈尔大学出版社。ISBN 0-8014-1350-8。
• Hahn, Roger (1982)。*皮埃尔·西蒙·拉普拉斯通信日历*。伯克利：加州大学伯克利分校科学与技术历史办公室。ISBN 978-0-918102-07-2。OCLC 8877709。
• Hahn, Roger (1994)。*皮埃尔·西蒙·拉普拉斯通信的新日历*。伯克利，加州：加州大学伯克利分校科学与技术历史办公室。ISBN 978-0-918102-20-1。OCLC 31967034。
• Hahn, Roger (2005)。*皮埃尔·西蒙·拉普拉斯，1749–1827：一个坚定的科学家*（意大利文）。剑桥，马萨诸塞州：哈佛大学出版社。ISBN 978-0-674-01892-1。OCLC 58457459。
• Israel, Werner (1987). "黑暗恒星：一个思想的演变"。收录于 Hawking, Stephen W.; Israel, Werner（主编）。*重力学 300 年*。剑桥大学出版社，第 199–276 页。
• O'Connor, John J.; Robertson, Edmund F.，"皮埃尔-西蒙·拉普拉斯"，*麦克图尔数学史档案*，圣安德鲁斯大学（1999 年）。
• Nikulin, M. (1992). "拉普拉斯定理的逆定理的一个备注"。*苏联数学杂志*。59（4）：976–979。doi:10.1007/bf01099128。S2CID 121149198。
• Rouse Ball, W.W. [1908] (2003) "皮埃尔·西蒙·拉普拉斯（1749–1827）"，收录于*数学史短评（第 4 版）*，多佛出版社，ISBN 0-486-20630-0。也可在古腾堡项目上获取。
• Stigler, Stephen M. (1975). "概率与统计史研究。XXXIV 拿破仑统计学：拉普拉斯的工作"。*生物统计学*。62（2）。JSTOR: 503–517。doi:10.2307/2335393。ISSN 0006-3444。JSTOR 2335393。
• Stigler, Stephen M. (1978). "拉普拉斯的早期工作：年表与引用"。*伊西斯*。69（2）。芝加哥大学出版社：234–254。Bibcode:1978Isis...69..234S。doi:10.1086/352006。ISSN 0021-1753。S2CID 143831269。
• Whitrow, Gerald James (2001)，"皮埃尔-西蒙·拉普拉斯侯爵"，*大英百科全书*（豪华 CD-ROM 版）。
• Whittaker, E. T. (1949a). "拉普拉斯"。*数学杂志*。33（303）：1–12。doi:10.2307/3608408。JSTOR 3608408。S2CID 250442315。
• Whittaker, Edmund (1949b). "拉普拉斯"。*美国数学月刊*。56（6）：369–372。doi:10.2307/2306273。JSTOR 2306273。
• Wilson, C. (1985). "木星与土星的大不等式：从开普勒到拉普拉斯"。*精确科学历史档案*。33（1–3）：15–290。Bibcode:1985AHES...33...15W。doi:10.1007/BF00328048。S2CID 121751666。
• Young, T. (1821). *拉普拉斯天体力学的基础插图：第一部分，包含第一卷*。伦敦：约翰·穆雷出版社 – 通过互联网档案馆。

21. 外部链接

• “拉普拉斯，皮埃尔（1749–1827）”。埃里克·魏斯坦的科学传记世界。沃尔夫勒姆研究公司。检索日期：2007 年 8 月 24 日。
• 《皮埃尔-西蒙·拉普拉斯》收录于 MacTutor 数学历史档案。
• 《鲍迪奇翻译的拉普拉斯前言》。天体力学。MacTutor 数学历史档案。检索日期：2007 年 9 月 4 日。
• 《皮埃尔·西蒙·拉普拉斯档案指南》，收录于班克罗夫特图书馆。
• 皮埃尔-西蒙·拉普拉斯在数学家族谱项目中的页面。
• 拉普拉斯关于概率和统计的大部分工作英语翻译，已归档于 2012 年 12 月 27 日（由理查德·普尔斯坎普提供），2012 年 10 月 29 日的 Wayback Machine 归档。
• 皮埃尔-西蒙·拉普拉斯——《完整作品》（仅最后 7 卷），Gallica-Math。
• “关于一个从高处落下的物体的运动”（拉普拉斯，1803 年），在线并已在 BibNum 分析，2015 年 4 月 2 日归档于 Wayback Machine（英文）。