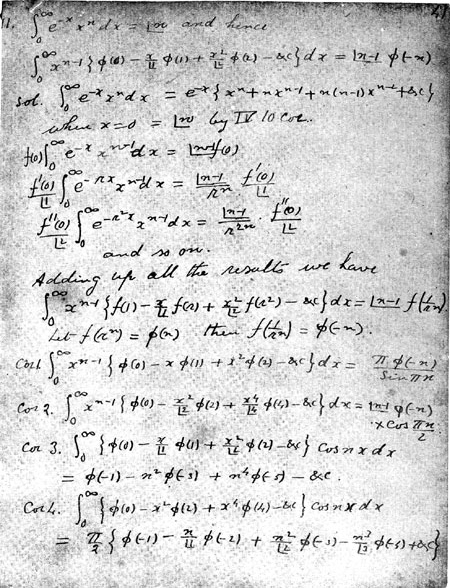斯里尼瓦瑟·拉马努金（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科 相关文章。

图
图 1：1913 年的拉马努金

　　 斯里尼瓦瑟·拉马努金·艾扬加尔（Srinivasa Ramanujan Aiyangar）FRS（1887 年 12 月 22 日－1920 年 4 月 26 日）是一位印度数学家。他常被视为史上最伟大的数学家之一。尽管几乎没有接受过纯数学的正规训练，他仍在数学分析、数论、无穷级数和连分数等领域做出了重要贡献，并提出了当时被认为无法解决的数学问题的解法。

　　 拉马努金最初是在孤立的环境中自行开展数学研究的。正如汉斯·艾森克所说：“他曾试图让当时最顶尖的职业数学家对他的研究产生兴趣，但大多数时候都失败了。他所展示的成果太新颖、太陌生，而且呈现方式也很不寻常；那些人懒得去理会。”\(^\text{[4]}\) 为了寻找能真正理解他工作的数学家，1913 年，他开始与英国剑桥大学的数学家 G.H.哈代通信。哈代意识到拉马努金的研究非同寻常，便为他安排了赴剑桥的行程。在笔记中，哈代评论道，拉马努金提出了具有突破性的全新定理，其中一些 “令我完全败下阵来；我从未见过任何类似的东西”，\(^\text{[5]}\) 还有一些则是刚刚被证明、极为高深的成果。

　　 在他短暂的一生中，拉马努金独立整理出了近 3900 条数学成果（主要是恒等式和方程）。\(^\text{[6]}\) 其中许多都是前所未见的原创成果；他那些独特而极不寻常的发现，如 “拉马努金素数”、“拉马努金θ函数”、“整数划分公式” 以及 “拟θ函数” 等，不仅开辟了全新的研究领域，也激发了大量后续研究。\(^\text{[7]}\) 在他成千上万的研究成果中，大多数后来都被证明是正确的。\(^\text{[8]}\) 以他的名字命名的《拉马努金期刊》应运而生，专门发表受他研究影响的各类数学成果。\(^\text{[9]}\) 他留下的笔记本——记录了他已发表和未发表成果的摘要——至今仍被数学家们分析和研究，成为不断涌现新数学思想的重要来源。直到 2012 年，研究者们仍不断发现，他笔记中那些仅以 “简单性质” 或 “相似结果” 带过的评论，其实暗藏着深奥而精妙的数论定理，且这些定理直到他去世近百年后才被真正识别出来。\(^\text{[10][11]}\) 拉马努金是最年轻的英国皇家学会会士之一，是第二位印度籍成员，也是首位当选剑桥大学三一学院会士的印度人。

　　 1919 年，健康状况恶化——如今被认为是由多年前痢疾引发的并发症 “肝阿米巴病” 所致——迫使拉马努金返回印度。他于 1920 年去世，年仅 32 岁。他在 1920 年 1 月写给哈代的最后几封信表明，他在生命的最后时刻仍在不断提出新的数学思想和定理。他的 “失落的笔记本”，记录了他生命最后一年中的诸多发现，于 1976 年被重新发现后，在数学界引起了极大的轰动。

1. 早年生活

图
图 2：拉马努金的出生地位于埃罗德阿拉希里街 18 号，现属于泰米尔纳德邦。

　　 拉马努金（意为 “罗摩的弟弟”，罗摩是印度教神祇）于 1887 年 12 月 22 日出生在现今泰米尔纳德邦的伊罗德市的一个泰米尔婆罗门艾扬加尔家庭中。他的父亲库普苏瓦米·斯里尼瓦萨·艾扬加尔原籍坦贾武尔区，在一家纱丽店当职员。他的母亲科玛拉塔玛尔是家庭主妇，也在当地庙宇中唱诵圣歌。他们一家住在库姆巴科纳姆镇的萨兰加帕尼圣殿街上的一间传统小屋里，该住宅如今已被改为博物馆。

　　 当拉马努金一岁半时，母亲生下了另一个儿子萨达戈潘，但他在出生不到三个月后夭折。1889 年 12 月，拉马努金感染了天花，不过他幸运地康复了，而当时坦贾武尔区约有 4000 人死于这一年严重的天花疫情。此后，他随母亲搬到了她父母位于康契布勒姆（今切奈附近）的家中。母亲随后又分别于 1891 年和 1894 年生下两个孩子，但这两个孩子都未能活过一岁。

　　 1892 年 10 月 1 日，拉马努金被送入当地学校就读。\(^\text{[17]}\) 后来，他的外祖父在康契布勒姆失去了担任法庭官员的职位，\(^\text{[18]}\) 拉马努金和母亲便搬回了库姆巴科纳姆，并在那里就读于康伽延初级学校。\(^\text{[19]}\) 随着祖父去世，他又被送回外祖父母位于马德拉斯（今金奈）的住所。但他不喜欢马德拉斯的学校，还经常试图逃课。他的家人甚至请了一位当地警察来监督他上学。不到六个月，拉马努金就再次回到了库姆巴科纳姆。\(^\text{[19]}\)

图
图 3：拉马努金位于库姆巴科纳姆萨兰加帕尼·桑尼迪街的故居

　　 由于拉马努金的父亲大部分时间在外工作，照顾他的任务主要由母亲承担，因此母子之间关系十分亲密。他从母亲那里学习传统和《往世书》，学唱宗教歌曲，参加寺庙的祈祷仪式（puja），并遵守特定的饮食习惯——这些都是婆罗门文化的一部分。\(^\text{[20]}\) 在康伽延初级学校，拉马努金表现出色。1897 年 11 月，在即将年满 10 岁时，他以全区最高分通过了英语、泰米尔语、地理和算术的初等考试。\(^\text{[21]}\) 同年，拉马努金进入了城镇高等中学，在那里他第一次正式接触到数学。\(^\text{[21]}\)

　　 拉马努金在 11 岁时就已是神童，他很快掌握了家中两位大学生房客所掌握的全部数学知识。后来，他借到了一本由 S. L. Loney 编写的《高等三角学》教材。\(^\text{[22][23]}\) 到 13 岁时，他不仅精通了书中的内容，还自主发现了一些复杂的定理。到了 14 岁，他已获得了多项优异成绩证书和学术奖项，并在整个求学阶段持续获奖。他还协助学校为大约 1200 名学生（每人需求不同）安排约 35 名教师的教学任务。\(^\text{[24]}\) 他总能在规定时间的一半内完成数学考试，并表现出对几何学和无穷级数的熟练掌握。1902 年，拉马努金学会了解三次方程的解法，后来又发展出一套解四次方程的方法。1903 年，他尝试解五次方程，却不知道此类方程无法用根式来求解。\(^\text{[25]}\)

　　 1903 年，16 岁的拉马努金从一位朋友那里借到了一本图书馆藏书——G. S. Carr 所编的《纯粹与应用数学初步成果概要》，这是一部包含 5000 个定理的合集。\(^\text{[26][27]}\) 据说拉马努金详细研究了书中的内容。\(^\text{[28]}\) 次年，他独立发展并研究了伯努利数，并将欧拉–马歇罗尼常数计算到小数点后 15 位。\(^\text{[29]}\) 当时他的同龄人表示 “很少能听懂他在讲什么”，并 “对他怀有敬畏之心”。\(^\text{[24]}\)

　　 1904 年从城镇高等中学毕业时，拉马努金因数学成绩优异获得了校长克里希纳斯瓦米·艾耶尔颁发的 K·兰加纳塔·拉奥数学奖。艾耶尔称拉马努金是 “杰出的学生，应当得到超过满分的分数”。\(^\text{[30]}\) 他获得奖学金进入库姆巴科纳姆的政府艺术学院学习，\(^\text{[31][32]}\) 但由于他对数学过于专注，无法集中精力学习其他科目，最终大部分课程不及格，并因此失去了奖学金。\(^\text{[33]}\)1905 年 8 月，拉马努金离家出走，前往维沙卡帕特南，随后在拉贾蒙德里停留了大约一个月。\(^\text{[33]}\) 他后来在马德拉斯（今金奈）的帕查亚帕学院注册入学。在那里，他数学考试合格，只解答他感兴趣的问题，其他题目则空着不写，但在英语、生理学和梵文等其他科目表现不佳。\(^\text{[35]}\) 拉马努金于 1906 年 12 月第一次参加文科士考试未通过，一年后再次失败。没有获得 FA 学位的他，离开了大学，继续独立从事数学研究，生活极度贫困，经常处于饥饿边缘。\(^\text{[36]}\)

　　 1910 年，23 岁的拉马努金与印度数学学会创始人 V·拉马斯瓦米·艾耶尔会面后，开始在马德拉斯的数学界获得认可，这也促成了他被马德拉斯大学接纳为研究人员。\(^\text{[37]}\)

2. 成年时期（在印度）

　　 1909 年 7 月 14 日，拉马努金与贾纳基（Janaki，亦作 Janakiammal；1899 年 3 月 21 日－1994 年 4 月 13 日）结婚。\(^\text{[38]}\) 贾纳基是他母亲一年前为他选定的新娘，当他们结婚时，她年仅十岁。\(^\text{[39][40][41]}\) 当时为女孩在年幼时安排婚姻并不罕见。贾纳基来自拉詹德拉姆，这是位于马鲁杜尔（现属卡鲁尔县）火车站附近的一个村庄。拉马努金的父亲并未参加婚礼仪式。\(^\text{[42]}\) 按照当时的习俗，婚后贾纳基仍在娘家居住了三年，直到她初潮来临。1912 年，她与拉马努金的母亲一同前往马德拉斯与拉马努金团聚。\(^\text{[43]}\)

图
图 4：拉马努金独自坐着

　　 婚后，拉马努金患上了睾丸鞘膜积液。\(^\text{[44]}\) 这种病可以通过一个常规的外科手术来治疗，手术会引流阴囊囊袋中堵塞的液体，但他的家庭无力承担手术费用。1910 年 1 月，一位医生自愿免费为他进行手术。\(^\text{[45]}\)

　　 手术成功后，拉马努金开始寻找工作。他住在朋友家里，一边挨家挨户地在马德拉斯寻找文书职位。为了赚钱，他还为准备 “文科学士” 考试的总统学院学生辅导功课。\(^\text{[46]}\)

　　 1910 年末，拉马努金再次生病。他担心自己的健康，对朋友 R·拉达克里希纳·艾耶说：“如果我不行了，就把这些[笔记本]交给 Singaravelu Mudaliar 教授（帕恰伊亚帕学院的数学教授），或是马德拉斯基督学院的英国教授爱德华·B·罗斯。”\(^\text{[47]}\) 病愈后，拉马努金从艾耶手中取回笔记本，乘火车从库姆巴科纳姆前往维鲁普拉姆，这是一座当时处于法国控制下的城市。\(^\text{[48][49]}\)1912 年，他与妻子和母亲搬到马德拉斯乔治镇的赛瓦·穆塔亚·穆达利街，在那里住了几个月。\(^\text{[50]}\)1913 年 5 月，在获得马德拉斯大学的研究职位后，拉马努金携家人搬到了特里普利凯恩。\(^\text{[51]}\)

追求数学事业

　　 1910 年，拉马努金结识了副税务官 V·拉马斯瓦米·艾耶，他是印度数学学会的创始人之一。\(^\text{[52]}\) 拉马努金希望能在艾耶工作的税务部门谋得一份差事，于是将自己的数学笔记展示给他看。艾耶后来回忆道：

　　 “我被那些笔记中非凡的数学成果所震撼。我实在不忍心把他的天才埋没在税务部门最底层的职位上。”\(^\text{[53]}\)

　　 艾耶给了拉马努金几封介绍信，让他去拜访在马德拉斯的数学家朋友们。\(^\text{[52]}\) 其中几位看过他的笔记后，给他写了推荐信，介绍他去见内洛尔的地方长官、同时也是印度数学学会秘书的 R·拉马钱德拉·拉奥。\(^\text{[54][55][56]}\) 拉奥对拉马努金的研究印象深刻，但一开始怀疑那些成果是否真是他本人所作。拉马努金提到他曾与孟买著名数学家萨尔达纳教授通信，对方虽然表示不太理解他的工作，但认定他并非骗子。\(^\text{[57]}\) 拉马努金的朋友 C·V·拉贾戈帕拉查里也出面说服拉奥打消对他学术诚实的怀疑。

　　 拉奥决定再给拉马努金一次机会，并认真听他讲解关于椭圆积分、超几何级数和他提出的发散级数理论。拉奥表示，最终正是这些内容令他确信拉马努金才华卓绝。\(^\text{[57]}\) 拉奥问他有什么要求，拉马努金答道，他需要的是工作和经济支持。拉奥答应资助他，并将他送往马德拉斯。拉马努金在拉奥的资助下继续进行研究。

　　 在艾耶的帮助下，拉马努金的部分研究成果发表在《印度数学学会期刊》上。\(^\text{[58]}\)

图
图 5

　　 他在该期刊中提出的第一个问题之一是求以下表达式的值：\(^\text{[30]}\) $$ \sqrt{1 + 2 \sqrt{1 + 3 \sqrt{1 + \cdots}}}~ $$ 他在三期期刊中等待了六个月，希望有人能给出这个问题的解答，但始终没有收到回应。最终，拉马努金自己给出了一个不完整的解答。\(^\text{[59]}\) 在他第一本笔记本的第 105 页中，他写下了一个可用于求解这个无限嵌套根式问题的等式： $$ x + n + a = \sqrt{ax + (n + a)^2 + x \sqrt{a(x + n) + (n + a)^2 + (x + n) \sqrt{\cdots}}}~ $$ 利用这个等式，只需设 $x = 2$、$n = 1$、$a = 0$，就可以得到期刊中所提出问题的答案为 3。\(^\text{[60]}\) 拉马努金为该期刊撰写了第一篇正式论文，内容是关于伯努利数的性质。他发现的一个性质是：伯努利数分数的分母（在 OEIS 中为序列 A027642）始终可以被 6 整除。他还设计出一种基于已有伯努利数计算 $B_n$ 的方法，其中一种方法如下：

　　 可以注意到，如果 $n$ 是偶数且不等于零：

  1. $B_n$ 是一个分数，且在最简形式下 $\frac{B_n}{n}$ 的分子是一个质数；
  2. $B_n$ 的分母中因子 2 和 3 各出现一次，且仅出现一次；
  3. $2n(2n - 1)\frac{B_n}{n}$ 是一个整数，因此 $2(2n - 1)B_n$ 是一个奇整数。

　　 在他 1911 年发表的 17 页论文《伯努利数的一些性质》中，拉马努金给出了三个证明、两个推论和三个猜想。\(^\text{[61]}\) 他最初的写作存在很多问题。正如期刊编辑 M. T. Narayana Iyengar 所指出的：

　　 “拉马努金先生的方法过于简洁且新颖，他的表述缺乏清晰与严谨，普通的数学读者若不习惯如此高强度的思维体操，几乎无法理解他。”\(^\text{[62]}\)

　　 拉马努金后来又写了一篇论文，并继续在《印度数学学会期刊》上提供数学问题。\(^\text{[63]}\)1912 年初，他在马德拉斯审计长办公室找了一份临时工作，月薪为 20 卢比，但只工作了几个星期。\(^\text{[64]}\) 在这份工作的末期，他申请了马德拉斯港务局总会计处的职位。

　　 在 1912 年 2 月 9 日的一封信中，拉马努金写道：

　　 尊敬的先生：

　　 我听说贵办公室有一职位空缺，特此提出申请。我已通过中学毕业考试，并学习至 F.A.（文凭），但由于若干不幸的原因未能继续深造。然而，我一直将全部时间用于数学研究与发展该学科。我可以有信心地说，如果我被录用，一定能胜任本职工作。因此，恳请您考虑予以录用为盼。\(^\text{[65]}\)

　　 他在申请信中附上了总督学院数学教授 E. W. Middlemast 的推荐信，信中称拉马努金是 “一位在数学方面具有非凡能力的青年”。\(^\text{[66]}\) 三周后，即 3 月 1 日，拉马努金收到录用通知，成为三级四等会计文员，月薪 30 卢比。\(^\text{[67]}\) 在工作中，他总是轻松迅速地完成任务，并将空闲时间用于数学研究。他的上司弗朗西斯·斯普林爵士以及同事、也是印度数学学会财务官的 S. Narayana Iyer 都非常鼓励他从事数学研究。\(^\text{[68]}\)

联系英国数学家

　　 1913 年春天，纳拉亚纳·艾耶、拉马钱德拉·拉奥和 E·W·米德尔马斯特尝试将拉马努金的数学成果介绍给英国数学家。伦敦大学学院的 M·J·M·希尔评论说，拉马努金的论文中充满了漏洞。\(^\text{[69]}\) 他表示，尽管拉马努金 “对数学有兴趣，也有一定的才能”，但他缺乏被数学界接受所需的教育背景与基础。\(^\text{[70]}\) 尽管希尔并未提出要收拉马努金为学生，但他对拉马努金的工作给予了认真细致的专业建议。在朋友们的帮助下，拉马努金起草了信件，写给剑桥大学的几位著名数学家。\(^\text{[71]}\)

　　 前两位教授，H. F. 贝克和 E. W. 霍布森，在收到拉马努金的论文后没有发表评论便退还了。\(^\text{[72]}\)1913 年 1 月 16 日，拉马努金写信给 G. H. 哈代，他通过阅读《无穷阶的阶数》（Orders of Infinity，1910）而认识这位数学家。\(^\text{[73][74]}\) 来自一位默默无闻数学家的九页数学公式起初让哈代怀疑这可能是一场骗局。\(^\text{[75]}\) 虽然哈代认出了一些拉马努金的公式，但另一些却 “几乎令人难以置信”。\(^\text{[76]: 494 }\) 其中一个令哈代惊叹的定理位于第三页底部（在 $0 < a < b + \frac{1}{2}$ 的条件下有效）： $$ \int_0^{\infty} \frac{1 + \frac{x^2}{(b+1)^2}}{1 + \frac{x^2}{a^2}} \times \frac{1 + \frac{x^2}{(b+2)^2}}{1 + \frac{x^2}{(a+1)^2}} \times \cdots \, dx = \frac{\sqrt{\pi}}{2} \cdot \frac{ \Gamma\left(a + \frac{1}{2}\right) \Gamma(b + 1) \Gamma(b - a + 1) }{ \Gamma(a) \Gamma\left(b + \frac{1}{2}\right) \Gamma\left(b - a + \frac{1}{2}\right) }.~ $$ 哈代还对拉马努金在无穷级数方面的其他工作印象深刻，例如： $$ 1 - 5\left(\frac{1}{2}\right)^3 + 9\left(\frac{1 \times 3}{2 \times 4}\right)^3 - 13\left(\frac{1 \times 3 \times 5}{2 \times 4 \times 6}\right)^3 + \cdots = \frac{2}{\pi}~ $$ 以及： $$ 1 + 9\left(\frac{1}{4}\right)^4 + 17\left(\frac{1 \times 5}{4 \times 8}\right)^4 + 25\left(\frac{1 \times 5 \times 9}{4 \times 8 \times 12}\right)^4 + \cdots = \frac{2\sqrt{2}}{\sqrt{\pi}\, \Gamma^2\left(\frac{3}{4}\right)}~ $$ 第一个结果早在 1859 年就已由 G·鲍尔发现。而第二个结果对哈代来说是全新的，它来源于一类被称为超几何级数的函数，这类函数最早由欧拉和高斯研究。哈代认为这些结果 “远比高斯在积分方面的工作更令人着迷”。\(^\text{[77]}\) 当哈代看到拉马努金手稿最后一页关于连分数的定理时，他说道这些定理 “完全把我打败了；我以前从未见过任何类似的东西”，\(^\text{[78]}\) 并补充道，“它们一定是真的，因为如果不是真的，就不会有人有这样的想象力去凭空编造出来。”\(^\text{[78]}\) 哈代让他的同事 J·E·利特尔伍德也看了这些论文，利特尔伍德也对拉马努金的天才感到震惊。与利特尔伍德讨论后，哈代得出结论：这些信件 “无疑是我所收到过的最非凡的”，拉马努金是 “一位顶尖的数学家，一个极其具有独创性和力量的人”。\(^\text{[76]: 494–495}\) 另一位同事 E·H·内维尔后来回忆道：“当时在剑桥的数学圈里，没有人会忘记这封信引起的轰动……其中没有一个定理是世界上最先进的数学考试中可能出现的题目。”\(^\text{[63]}\)

　　 1913 年 2 月 8 日，哈代给拉马努金写了一封信，表达了对他研究的兴趣，并补充道：“我必须看到你某些论断的证明，这一点至关重要。” 在这封信于 2 月第三周抵达马德拉斯之前，哈代已经联系了英属印度事务办公室，着手安排拉马努金前往剑桥的行程。\(^\text{[79]}\) 印度学生咨询委员会秘书亚瑟·戴维斯会见了拉马努金，讨论出国事宜。\(^\text{[80]}\) 但出于婆罗门的传统信仰，拉马努金拒绝 “前往异国他乡”，他的父母也出于相同的原因表示反对。\(^\text{[81]}\) 与此同时，拉马努金给哈代寄去了一封塞满定理的信，并写道：“我在您身上找到了一个能同情我的努力的朋友。”\(^\text{[82]}\)

　　 为了补充哈代的推荐，剑桥大学三一学院前数学讲师吉尔伯特·沃克审阅了拉马努金的研究成果，并表示十分惊叹，强烈建议这位年轻人前往剑桥深造。\(^\text{[83]}\) 得到沃克的支持后，工程学院的数学教授 B·哈努曼塔·拉奥邀请拉马努金的同事纳拉亚纳·艾耶出席数学研究委员会的会议，以讨论 “我们能为 S·拉马努金做些什么”。\(^\text{[84]}\) 委员会最终同意为拉马努金提供马德拉斯大学为期两年的每月 75 卢比的研究奖学金。\(^\text{[85]}\)

　　 在担任研究生期间，拉马努金继续向《印度数学学会期刊》投稿。在一次投稿中，艾耶代为提交了拉马努金关于级数求和的一些定理，并附言写道：“以下定理出自马德拉斯大学的数学学生 S·拉马努金。” 同年 11 月，马德拉斯基督学院的英国教授爱德华·B·罗斯——几年前曾与拉马努金见过面——有一天突然神情激动地冲进教室，眼睛发亮地问学生们：“拉马努金懂波兰语吗？” 原因是拉马努金在某篇论文中预见了一位波兰数学家的研究成果，而这位波兰学者的论文正好在当天的邮件中抵达。\(^\text{[86]}\) 在他定期发表的论文中，拉马努金提出了使定积分更容易求解的定理。他以朱利亚诺·弗鲁拉尼（1821 年的积分定理为基础，提出了可以用来计算原本难以求解的积分的一般化公式。\(^\text{[87]}\)

　　 拉马努金拒绝前往英国后，他与哈代的通信关系一度恶化。为此，哈代请在马德拉斯任教的同事 E.H. 内维尔（E. H. Neville）出面指导并劝说拉马努金前往英国。\(^\text{[88]}\) 内维尔问拉马努金为何不愿去剑桥。此时拉马努金似乎已经接受了这个提议；内维尔说：“拉马努金并不需要被说服”，“他的父母也已不再反对”。\(^\text{[63]}\) 据说，拉马努金的母亲做了一个生动的梦，梦见儿子被欧洲人环绕，家族的守护神——纳马吉里的女神在梦中命令她 “不再阻碍儿子实现人生使命”。\(^\text{[63]}\)1914 年 3 月 17 日，拉马努金乘船启程前往英国，\(^\text{[89]}\) 将妻子留在印度与父母同住。\(^\text{[90]}\)

3. 英国生活

图
图 6：拉马努金（中）与同事 G·H·哈代（最右），以及其他科学家一起，摄于剑桥大学参议院大楼外，约 1914–1919 年。

　　 1914 年 3 月 17 日，拉马努金从马德拉斯乘坐 “内瓦萨号” 轮船启程离境。\(^\text{[91][92]}\)4 月 14 日他抵达伦敦时，内维尔已开车在港口等候。四天后，内维尔将他带到自己位于剑桥切斯特顿路的住所。拉马努金随即开始与利特尔伍德和哈代展开工作。六周后，拉马努金搬出内维尔家，搬进威尔庭院居住，那里距离哈代的房间仅五分钟步行路程。\(^\text{[93]}\)

　　 哈代和利特尔伍德开始研究拉马努金的笔记本。哈代此前在拉马努金的前两封信中已经收到了 120 个定理，但笔记本中还有更多的结果和定理。哈代发现其中一些是错误的，一些早已被他人发现，而其余的则是全新的突破。\(^\text{[94]}\) 拉马努金给哈代和利特尔伍德留下了深刻印象。利特尔伍德评论道：“我相信他至少可以媲美雅可比”，\(^\text{[95]}\) 而哈代则说：“我只能把他拿来和欧拉或雅可比相比。”\(^\text{[96]}\)

图
图 7：剑桥大学三一学院的惠威尔庭院

　　 拉马努金在剑桥与哈代和利特尔伍德合作了将近五年，并在此期间发表了部分研究成果。哈代和拉马努金的性格截然不同，他们的合作是一场文化、信仰和工作方式的碰撞。在此前的几十年里，数学基础受到了质疑，对严格数学证明的需求也逐渐被认可。哈代是无神论者，是数学证明和严谨性的坚定信奉者，而拉马努金则是一个虔诚的宗教信徒，他极其依赖直觉与洞察力。哈代尽最大努力弥补拉马努金在教育上的空白，指导他理解用形式化证明来支撑结果的重要性，同时又不压抑他的灵感——这场张力对双方来说都并不轻松。

图
图 8：拉马努金的“主定理”手稿页

　　 1916 年 3 月，拉马努金因其关于 “高度合成数” 的研究被授予 “研究型文学士学位”，这是如今博士学位的前身。该研究的第一部分已于前一年发表在《伦敦数学会会刊》上。论文长达 50 多页，证明了这类数的多种性质。尽管哈代本人并不喜欢这一研究方向，他仍评价说，虽然该研究涉及的是他称之为 “数学的支流” 领域，拉马努金在其中展现了 “对不等式代数的非凡掌握力”。

　　 1917 年 12 月 6 日，拉马努金被选为伦敦数学学会会员。1918 年 5 月 2 日，他当选为英国皇家学会院士，成为继 1841 年阿达西尔·柯塞吉之后第二位获此殊荣的印度人。当时年仅 31 岁的他，也成为皇家学会历史上最年轻的院士之一。他的当选理由是 “在椭圆函数和数论方面的研究成果”。同年 10 月 13 日，他又成为剑桥大学三一学院的院士，成为首位获此殊荣的印度人。

4. 疾病与逝世

　　 拉马努金一生中饱受健康问题困扰。他在英格兰期间健康状况恶化；这可能部分是因为他难以坚持宗教所要求的严格饮食习惯，加之 1914 年至 1918 年间的一战配给制度，使他身体更为虚弱。他被诊断患有肺结核以及严重的维生素缺乏症，并被送入疗养院。1917 年底或 1918 年初，他曾试图自杀，跳入伦敦地铁的铁轨。苏格兰场以企图自杀（在当时属于犯罪）将他逮捕，但在哈代介入后将其释放。[102][103]1919 年，拉马努金返回马德拉斯省的库姆巴科南，1920 年逝世，年仅 32 岁。他去世后，他的弟弟蒂鲁纳拉亚南整理了他留下的手稿笔记，内容包括关于奇异模数、超几何级数和连分数的公式。\(^\text{[43]}\) 据贾纳基·阿姆马尔回忆，在临终的日子里，尽管忍受着剧痛，拉马努金 “仍不断做数学研究，一页又一页地写满了数字”。\(^\text{[104]}\)

　　 拉马努金的遗孀贾纳基·阿姆马尔夫人搬到了孟买。1931 年，她返回马德拉斯，并定居在特里普利凯恩，依靠马德拉斯大学提供的养老金和缝纫工作所得维持生计。1950 年，她收养了一名儿子 W·纳拉亚南，他后来成为印度国家银行的一名职员，并组建了家庭。在她晚年，拉马努金的前雇主马德拉斯港务局为她提供了终身养老金，此外她还领取了印度国家科学学院以及泰米尔纳德邦、安得拉邦和西孟加拉邦等地政府发放的养老金。她一直珍视拉马努金的记忆，并积极参与提高其公众认知的相关工作。包括乔治·安德鲁斯、布鲁斯·C·伯恩特和贝拉·博洛巴斯在内的著名数学家在访问印度时，都会特意拜访她。她于 1994 年在特里普利凯恩的住所去世。\(^\text{[42][43]}\)

　　 1994 年，D. A. B. Young 对拉马努金的病历和症状进行了分析，\(^\text{[103]}\) 得出的结论是：与肺结核相比，拉马努金的病症——包括他以往的复发、发热和肝脏问题——更符合 “肝阿米巴病” 的表现，这是一种当时在马德拉斯广泛流行的疾病。他在离开印度之前曾经历过两次痢疾发作。当痢疾未被妥善治疗时，阿米巴痢疾可以潜伏多年，并发展为肝阿米巴病，而这种疾病在当时尚未被医学界充分认识。\(^\text{[105]}\) 在当时，如果能够得到正确诊断，阿米巴病是一种可治疗且通常可以治愈的疾病；\(^\text{[105][106]}\) 第一次世界大战期间，感染阿米巴病的英国士兵就在拉马努金离开英国前后被成功治愈了。\(^\text{[107]}\)

5. 性格与精神生活

　　 拉马努金被描述为一个有些害羞、沉默寡言的人，是一位举止得体、性格温和的人。\(^\text{[109]}\) 他在剑桥过着简朴的生活。\(^\text{[110]}\) 拉马努金的第一批印度传记作者称他是一个严格遵守正统印度教信仰的人。他将自己的数学才智归功于家族的守护女神——纳马卡尔的那玛吉丽·塔亚（即女神摩哈拉克希米）。他在工作中向她寻求灵感，\(^\text{[111]}\) 并称自己曾梦见象征她配偶那罗辛哈的血滴。后来，他又梦见展现在眼前的一卷卷写满复杂数学内容的卷轴。\(^\text{[112]}\) 他常说：“对我而言，一个公式如果不能表达神的思想，就毫无意义。”\(^\text{[113]}\)

　　 哈代曾引用拉马努金的话说，所有宗教在他看来似乎都同样真实。\(^\text{[114]}\) 哈代进一步认为，拉马努金的宗教信仰被西方人过度浪漫化了，也被印度传记作者在 “信仰” 而非 “实践” 层面上夸大了。同时，他也提到拉马努金严格奉行素食主义。\(^\text{[115]}\)

　　 同样，在接受《Frontline》采访时，伯恩特表示：“许多人错误地将拉马努金的数学思维神秘化，这不属实。他在三本笔记本中严谨地记录了每一个结果。” 他还推测，拉马努金可能是在石板上推导中间步骤的，因为他负担不起足够的纸张来做更永久的记录。\(^\text{[8]}\)

　　 伯恩特提到，贾纳基在 1984 年说，拉马努金把大量时间都花在数学上，以至于没有时间去寺庙，她和母亲经常喂他吃饭，因为他顾不上吃饭，而许多与他有关的宗教故事其实是别人附会的。不过，他在宗教仪式实践方面的虔诚并无疑问。\(^\text{[116]}\)

6. 数学成就

　　 在数学中，洞察力与推导证明之间存在着区别。拉马努金提出了大量可以供后来深入研究的公式。G.H. 哈代曾说，拉马努金的发现异常丰富，往往远不止表面上看起来那么简单。作为他工作的副产品，一些全新的研究方向也由此被开启。其中最令人着迷的一些公式包括用于计算 $\pi$ 的无穷级数，下列即是其中之一： $$ \frac{1}{\pi} = \frac{2\sqrt{2}}{9801} \sum_{k=0}^{\infty} \frac{(4k)!(1103 + 26390k)}{(k!)^4 396^{4k}}.~ $$ 这一结果基于负的基本判别式 $d = -4 \times 58 = -232$，其类数 $h(d) = 2$。此外，26390 = 5 × 7 × 13 × 58，且 16 × 9801 = 396²，这与以下事实有关： $$ e^{\pi \sqrt{58}} = 396^4 - 104.000000177\ldots~ $$ 这可与类数为 1 的 Heegner 数相比，后者也导出了类似的公式。

　　 拉马努金的 $\pi$ 级数收敛速度极快，是当今一些计算 $\pi$ 的最快算法的基础。仅取该级数的首项，即可得到近似值： $$ \pi \approx \frac{9801\sqrt{2}}{4412}~ $$ 这一值在小数点后六位是准确的；取前两项可得出精确到 14 位小数的 π 值（参见更通用的拉马努金–佐藤级数）。

　　 拉马努金的非凡能力之一，是他能迅速解决问题。以下这个轶事生动地展示了这一点，当时 P.C. 马哈拉诺比斯向他提出了一个问题：

　　 “想象你站在一条街上，街道上的房子编号从 1 到 $n$。其中有一所房子 $x$，它左边所有房号之和，等于它右边所有房号之和。如果 $n$ 在 50 到 500 之间，求出 $n$ 和 $x$。” 这是一个双变量问题，存在多个解。拉马努金思索了一会儿，给出了一个 “意料之外” 的答案：他写下了一个连分数。这不寻常之处在于——它是这类问题的通解。马哈拉诺比斯大为震惊，问他是怎么做到的。拉马努金回答说：“这很简单。我一听到这个问题，就知道答案是一个连分数。接着我问自己，是哪一个连分数？然后答案就在脑海里浮现出来了。”

　　 他的直觉也引导他推导出了一些此前未知的恒等式，例如： $$ \left(1+2\sum_{n=1}^{\infty} \frac{ \cos\left(n\theta\right) }{ \cosh\left(n\pi\right) }\right)^{-2} + \left(1+2\sum_{n=1}^{\infty} \frac{ \cosh\left(n\theta\right) }{ \cosh\left(n\pi\right) }\right)^{-2} = \frac{2\Gamma^4\left(\frac{3}{4}\right)}{\pi} = \frac{8\pi^3}{\Gamma^4\left(\frac{1}{4}\right)}~ $$ 其中 $\theta$ 满足： $$ | \operatorname{Re} (\theta)| < \pi,\quad | \operatorname{Im} (\theta)| < \pi~ $$ $\Gamma(z)$ 是伽马函数，该恒等式也与 Dedekind η 函数的一个特殊值有关。将该公式展开为幂级数，并比较其中 $\theta^0$、$\theta^4$ 和 $\theta^8$ 的系数，可以得到一些关于双曲正割函数的深刻恒等式。

　　 1918 年，哈代与拉马努金深入研究了整数分拆函数 $P(n)$，他们给出了一个非收敛的渐近级数公式，可以用来精确计算一个整数的分拆数。1937 年，汉斯·拉德马赫对其公式进行了改进，找到了该问题的一个收敛级数解。拉马努金与哈代在该领域的工作催生了一种强大的新方法——圆法，用于求解渐近公式。\(^\text{[119]}\)

　　 在生命的最后一年，拉马努金发现了 “拟 $\theta$ 函数”。\(^\text{[120]}\) 这些函数在很长时间内都是数学谜题，如今人们已经知道它们是调和弱 Maass 形式的全纯部分。

拉马努金猜想

　　 尽管有许多命题都可被称为 “拉马努金猜想”，但其中一个在后来的研究中影响尤为深远。特别是该猜想与安德烈·韦伊在代数几何中的一系列猜想之间的联系，开启了新的研究领域。这个著名的拉马努金猜想是关于 $\tau$ 函数（tau-function）大小的断言，它的生成函数是判别式模形式 $\Delta(q)$，这是模形式理论中典型的尖点形式。1973 年，皮埃尔·德利涅在证明韦伊猜想的过程中，最终证明了该猜想。该证明所涉及的化简步骤非常复杂，德利涅也因此在 1978 年获得了菲尔兹奖。\(^\text{[7][121]}\)

　　 在其论文《论某些算术函数》中，拉马努金定义了所谓的 $\Delta$ 函数，其系数称为 $\tau(n)$，即 “拉马努金 $\tau$ 函数”。\(^\text{[122]}\) 他证明了许多关于这些数的同余关系，例如对素数 $p$ 有：$\tau(p) \equiv 1 + p^{11} \pmod{691}$ 这类同余式（以及拉马努金证明的其它同类同余）启发了让-皮埃尔·塞尔（Jean-Pierre Serre，1954 年菲尔兹奖得主）提出猜想：存在一个伽罗瓦表示理论，可以 “解释” 这些同余关系，并更广泛地解释所有模形式。$\Delta(z)$ 是第一个以这种方式被研究的模形式。德利涅在其获得菲尔兹奖的工作中证明了塞尔的猜想。而费马大定理的证明也正是通过将椭圆曲线与模形式重新用这些伽罗瓦表示进行解释开始的。没有这套理论，费马大定理就无法被证明。\(^\text{[123]}\)

拉马努金的笔记本

　　 拉马努金在马德拉斯期间，将他大部分的数学成果记录在四本活页笔记本中。这些笔记本中的内容大多未附推导过程。这很可能是 “拉马努金无法证明其定理、只是直接得出结论” 这一误解的来源。数学家布鲁斯·C·伯恩特在回顾这些笔记和拉马努金的研究时指出，拉马努金实际上完全有能力证明他的大多数结果，但他选择不在笔记中写出完整的证明。

　　 其中可能有多种原因。由于当时纸张价格昂贵，拉马努金大多在石板上进行演算（可能包括证明过程），之后才将最终结果誊写到纸上。在马德拉斯省，数学学生普遍使用石板进行练习。此外，他很可能受到 G.S. Carr 那本书风格的影响——该书只是陈述结论，不附证明。他也可能认为自己的工作只是出于个人兴趣，因此仅记录结论。\(^\text{[124]}\)

　　 第一本笔记本有 351 页，包括 16 个相对有组织的章节和一些零散材料；第二本有 256 页、21 个章节以及 100 页未整理内容；第三本有 33 页未整理材料。这些笔记中的成果激发了后来众多数学家撰写论文，尝试证明他发现的公式。哈代本人曾写论文探讨拉马努金的部分内容，G.N. Watson、B.M. Wilson 以及布鲁斯·伯恩特也都如此。\(^\text{[124]}\)

　　 1976 年，乔治·安德鲁斯在一次图书馆偶然发现了第四本笔记——包含 87 页未整理材料，即所谓的 “遗失的笔记本”。\(^\text{[105]}\)

7. 哈代–拉马努金数 1729

　　 数字 1729 被称为 “哈代–拉马努金数”，源自一次哈代探望拉马努金时发生的著名对话。据哈代回忆道：\(^\text{[125]}\)

　　 “我记得有一次去普特尼医院看望他，那天我坐的是一辆编号为 1729 的出租车。我顺口说了句，这个数字看起来挺无聊的，希望不是个不吉利的征兆。他马上回答说：‘不，它是一个非常有趣的数字；它是最小的可以用两种不同方式表示为两个立方数之和的数字。’”

　　 在讲述这个轶事前，哈代还引用了利特尔伍德的一句话：“每一个正整数，都是拉马努金的私人朋友。”\(^\text{[126]}\)

　　 这两种表示方式是： $$ 1729 = 1^3 + 12^3 = 9^3 + 10^3~ $$ 这一想法的推广，催生了 “出租车数” 的概念。

8. 数学家们对拉马努金的看法

　　 在 1920 年为《自然》杂志撰写的拉马努金讣告中，哈代指出拉马努金的研究主要集中在即便在其他纯数学家中也鲜有人涉足的领域，并总结道：

　　 他对公式的洞察力令人惊叹，远远超过我在任何一位欧洲数学家中所见过的。或许去猜测，如果他在 16 岁而不是 26 岁便接触到了现代的数学思想与方法，会有怎样的发展并无太大意义。但我们完全可以合理设想，他本可以成为他那个时代最伟大的数学家。他实际所取得的成就已经足够令人赞叹……等到由他的工作所启发的研究完成之后，人们很可能会认为他所做的一切，比我们今天所认识到的还要更加惊人。\(^\text{[76]}\)

　　 哈代进一步说道：\(^\text{[128]}\)

　　 他兼具高度的概括能力、对数学形式的敏感直觉，以及迅速调整自己假设的能力，这些特质常常令人震惊，使他在自己独特的领域中，在当时无与伦比。他知识的局限性与其深度一样令人惊讶。他是这样一个人：能够推导出前所未闻阶数的模方程和定理；对连分数的掌握远超当时世上任何数学家；他自行找出了黎曼ζ函数的函数方程以及解析数论中许多著名问题的主导项；然而他却从未听说过双周期函数或柯西定理，甚至对复变函数的概念都只有极为模糊的认识……

　　 作为一个例子，哈代评论了拉马努金第一封信中的 15 个定理。其中，前 13 个是正确且富有洞察力的，第 14 个是不正确但仍有启发意义的，第 15 个是正确但具有误导性的。

　　 （第 14 个定理）：在表达式 $\left(1 - 2x + 2x^4 - 2x^9 + \cdots \right)^{-1}$ 中，$x^n$ 的系数是最接近以下数值的整数： $$ \frac{1}{4n} \left( \cosh\left(\pi \sqrt{n}\right) - \frac{ \sinh\left(\pi \sqrt{n}\right) }{\pi \sqrt{n}} \right)~ $$ 哈代评价说，这个定理 “是他提出过的最富成果的之一，因为它最终引领我们走向了所有关于整数分拆问题的联合研究”。\(^\text{[129]}\)

　　 当被问及拉马努金是如何得出他的解答时，哈代表示这些结果是 “通过一种混合了推理、直觉和归纳的过程得到的，而他完全无法对这一过程作出连贯的解释。”\(^\text{[130]}\) 他还说，自己 “从未遇见过他的对等者，只能将他与欧拉或雅可比相提并论”。\(^\text{[130]}\) 哈代认为，拉马努金的研究风格属于 19 世纪的传统风格，即得出正确公式比建立系统的形式理论更为重要。他认为拉马努金在代数学方面成就最为卓越，尤其是在超几何级数和连分数方面。\(^\text{[129]}\)

　　 可能公式的辉煌时代已经过去，拉马努金本该早出生一百年；但在他那个时代，他无疑是最伟大的公式大师。过去五十年中，确实有一些数学家更重要，也许必须说是更伟大，但没有一个能在拉马努金擅长的领域与他匹敌。在他擅长的游戏中，他可以让任何数学家十五子再开局。\(^\text{[129]}\)

　　 他在数学分析方面的新发现较少，可能是因为缺乏正规教育，也找不到相关书籍学习；但他重新发现了许多结果，包括素数定理。在分析领域，他研究了椭圆函数和数的解析理论。在解析数论方面，他一如既往地富有想象力，但他想象出的许多内容是错误的。哈代将此归因于解析数论本身的困难，因为想象力曾令许多伟大的数学家在这一领域误入歧途。在解析数论中，严谨的证明比想象力更重要，而这正好与拉马努金的风格相反。他 “唯一的重大失败” 是他 “对解析函数理论一无所知”。\(^\text{[129]}\)

　　 据说利特尔伍德曾表示，帮助拉马努金赶上欧洲数学的进展非常困难，因为每当向拉马努金讲解一个新点，他就会立刻产生原创性想法，导致课程无法继续进行。\(^\text{[131]}\)

　　 K·斯里尼瓦萨·拉奥曾说：\(^\text{[132]}\) “至于他在数学世界中的地位，我们引用布鲁斯·C·伯恩特的话：‘保罗·埃尔德什曾转述哈代对数学家的个人评分。假设我们按照纯粹天赋以 0 到 100 的评分标准衡量数学家，哈代给自己的分数是 25，给 J·E·利特尔伍德是 30，大卫·希尔伯特是 80，而拉马努金是 100。’” 伯恩特还在 2011 年 5 月于印度理工学院马德拉斯分校的一次讲座中表示，在过去 40 年里，随着拉马努金几乎所有的猜想被证明，人们对他工作和才华的欣赏日益增长；如今，拉马努金的工作已经渗透进现代数学与物理的多个领域。\(^\text{[120][133]}\)

9. 身后荣誉

图
图 9

　　 “拉马努金去世后的第二年，《自然》杂志将他与其他杰出的科学家和数学家一同列入‘科学先锋年历’中，以表彰其卓越成就。\(^\text{[134]}\) 拉马努金的家乡泰米尔纳德邦将他的生日——12 月 22 日——定为‘邦信息技术日’。印度政府分别于 1962 年、2011 年、2012 年和 2016 年发行了印有拉马努金肖像的邮票。\(^\text{[135]}\)

　　 自拉马努金诞辰百年起，他的生日 12 月 22 日每年都在他曾就读的金伯高南政府艺术学院和清奈的印度理工学院马德拉斯分校被庆祝为 “拉马努金日”。国际理论物理中心与国际数学联盟合作，以拉马努金之名设立了一个奖项，用以表彰来自发展中国家的年轻数学家，该联盟负责提名评奖委员会成员。位于泰米尔纳德邦的一所私立大学——萨斯特拉大学也设立了 “萨斯特拉·拉马努金奖”（，奖金为 1 万美元，每年颁发给不超过 32 岁、在拉马努金研究影响领域中做出杰出贡献的数学家。\(^\text{[136]}\)”

　　 根据印度大学拨款委员会指定的委员会的建议，由萨斯特拉大学设立的斯里尼瓦瑟·拉马努金中心已被正式宣布为萨斯特拉大学的校外教学中心。该中心所在校园还设有 “拉马努金数学之家” 博物馆，展示拉马努金的生平与数学贡献。萨斯特拉大学还购买并修缮了位于金伯高南的拉马努金故居。\(^\text{[136]}\)

　　 2011 年，为纪念拉马努金诞辰 125 周年，印度政府宣布每年 12 月 22 日为 “国家数学日”。\(^\text{[137]}\) 时任印度总理曼莫汉·辛格还宣布，2012 年将作为 “国家数学年” 予以庆祝，而 12 月 22 日定为 “印度国家数学日”。\(^\text{[138]}\)

　　 “拉马努金信息技术城” 是位于金奈的一座信息技术特别经济区），建成于 2011 年，毗邻 Tidel 信息技术园区，占地约 25 英亩（10 公顷），包括两个分区，总建筑面积约为 570 万平方英尺（53 万平方米），其中办公空间达 450 万平方英尺（42 万平方米）。\(^\text{[139]}\)

10. 纪念邮票

　　 印度邮政发行的拉马努金纪念邮票（按年份排列）：

图
图 10

11. 在流行文化中

12. 精选论文

13. 拉马努金数学的后续著作

14. 拉马努金及其研究的精选出版物

15. 拉马努金相关著作的精选出版物

16. 另见

17. 脚注

　　 a,/ˈsriːnɪvɑːsə rɑːˈmɑːnʊdʒən/（斯里-尼-瓦-萨 拉-马-努-詹）；\(^\text{[1]}\) 泰米尔语发音：[sriːniʋaːsa ɾaːmaːnud͡ʑan ajːaŋgar]\(^\text{[2][3]}\)

18. 参考文献

  1. Olausson, Lena；Sangster, Catherine（2006 年）。《牛津 BBC 发音指南》。牛津大学出版社，第 322 页。ISBN 978-0-19-280710-6。
  2. Kanigel, Robert（2004 年）。〈拉马努金，斯里尼瓦瑟〉，《牛津国家传记辞典》（网络版）。牛津大学出版社。doi:10.1093/ref\:odnb/51582。（需要订阅或英国公共图书馆会员身份。）
  3. “拉马努金·艾扬加尔，斯里尼瓦瑟（1887–1920）”。trove.nla.gov.au。
  4. 汉斯·艾森克（1995 年）。《天才》，第 197 页。剑桥大学出版社，ISBN 0-521-48508-8。
  5. 哈代，戈弗雷·哈罗德（1940 年）。《拉马努金：基于其生平和工作所引发的十二讲》。剑桥大学出版社，第 9 页。1978 年第三版，经美国数学会切尔西出版公司 2021 年修订重印，ISBN 0-8218-2023-0。
  6. 伯恩特，布鲁斯·C.（1997 年 12 月 12 日）。《拉马努金笔记》第五卷。施普林格科学与商务媒体，第 4 页。ISBN 978-0-38794941-3。
  7. 小野贤（2006 年 6 月至 7 月）。〈致敬来自库姆巴科南的天赋〉（PDF）《美国数学会通报》，第 53 卷第 6 期：640–651［特别参考 649–650 页］。存档自 2007 年 6 月 21 日的原始版本。访问时间：2007 年 6 月 23 日。
  8. “重识拉马努金”。《前线》杂志，第 16 卷第 17 期：第 650 页。1999 年 8 月。原始版本存档于 2013 年 9 月 25 日。访问时间：2012 年 12 月 20 日。
  9. Alladi, Krishnaswami；Elliott, P. D. T. A.；Granville, A.（1998 年 9 月 30 日）。《解析与初等数论：献给数学传奇保罗·埃尔德什的致敬》。施普林格科学与商务媒体，第 6 页。ISBN 978-0-79238273-7。
  10. “拉马努金‘简单’模式中的深层意义”。《新科学家》杂志。原始页面存档于 2017 年 8 月 3 日。
  11. “数学证明揭示拉马努金天才的魔力”。《新科学家》杂志。页面存档于 2017 年 7 月 9 日（Wayback Machine）。
  12. Kanigel 1991，第 12 页。
  13. Kanigel 1991，第 11 页。
  14. Kanigel 1991，第 17–18 页。
  15. Berndt 与 Rankin 2001，第 89 页。
  16. Srinivasan, Pankaja（2012 年 10 月 19 日）。〈怀旧公式〉。《印度教徒报》。访问于 2016 年 9 月 7 日。
  17. Kanigel 1991，第 13 页。
  18. Kanigel 1991，第 19 页。
  19. Kanigel 1991，第 14 页。
  20. Kanigel 1991，第 20 页。
  21. Kanigel 1991，第 25 页。
  22. Berndt 与 Rankin 2001，第 9 页。
  23. Hardy, G. H.（1999）。《拉马努金：源于其生平与工作的十二次讲座》。罗德岛州普罗维登斯：美国数学学会，第 2 页。ISBN 978-0-8218-2023-0。
  24. Kanigel 1991，第 27 页。
  25. “斯里尼瓦瑟·拉马努金 - 传记”。数学历史网。检索于 2022 年 10 月 29 日。
  26. Kanigel 1991，第 39 页。
  27. McElroy, Tucker（2005）。《数学家词典 A to Z》。Facts on File，第 221 页。ISBN 0-8160-5338-3。
  28. Ramanujan Aiyangar, Srinivasa；Hardy, Godfrey Harold；Aiyar, P. Veṅkatesvara Seshu（2000），《斯里尼瓦瑟·拉马努金论文集》，《自然》，第 123 卷（第 3104 期）：xii，Bibcode:1929Natur.123..631L，doi:10.1038/123631a0，ISBN 978-0-8218-2076-6，S2CID 44812911。
  29. Kanigel 1991，第 90 页。
  30. Kanigel 1991，第??页。
  31. Kanigel 1991，第 28 页。
  32. Kanigel 1991，第 45 页。
  33. Kanigel 1991，第 47–48 页。
  34. “拉马努金失而复得：1905 年《印度教徒报》中的一封信”。《印度教徒报》，印度金奈，2011 年 12 月 25 日。
  35. Krishnamachari, Suganthi（2013 年 6 月 27 日）。“一位天才的磨难”。《印度教徒报》。存档于 2017 年 8 月 26 日。检索于 2016 年 9 月 7 日。
  36. Kanigel 1991，第 55–56 页。
  37. Krishnamurthy, V. “斯里尼瓦瑟·拉马努金——他的生平与天赋”。[www.krishnamurthys.com。（该讲座为 1987 年 9 月 16 日在班加罗尔印度科学研究院维斯维萨拉雅礼堂拉马努金百年纪念活动中的一次专题演讲）。存档于 2016 年 9 月 21 日。检索于 2016 年 9 月 7 日。](http://www.krishnamurthys.com。（该讲座为 1987 年 9 月 16 日在班加罗尔印度科学研究院维斯维萨拉雅礼堂拉马努金百年纪念活动中的一次专题演讲）。存档于 2016 年 9 月 21 日。检索于 2016 年 9 月 7 日。)
  38. “裁缝与数学家”。Live Mint，2018 年 4 月 20 日。
  39. Kanigel 1991，第 71 页。
  40. Bullough, V.L.（1990）。“2. 西方社会中成年人对儿童与青少年的性行为历史”。《恋童癖：生物社会维度》。纽约：施普林格出版社，第 71 页。ISBN 978-1-46139684-0。
  41. Kolata, Gina（1987 年 6 月 19 日）。“回忆‘神奇的天才’”。《科学》（新系列），236（4808）：1519–21。Bibcode:1987Sci...236.1519K。doi:10.1126/science.236.4808.1519。PMID 17835731。
  42. “拉马努金的妻子：贾纳基亚玛尔（贾纳基）”(PDF)。《金奈：数学科学研究所》。原始 PDF 存档于 2012 年 12 月 24 日。检索于 2012 年 11 月 10 日。
  43. Janardhanan, Arun（2015 年 12 月 6 日）。“通向无限之路”。《印度快报》。原始链接于 2016 年 9 月 5 日存档。检索于 2016 年 9 月 7 日。
  44. Kanigel 1991，第 72 页。
  45. 拉马努金，斯里尼瓦瑟（1968）。P. K. 斯里尼瓦桑（编）《拉马努金纪念集：书信与回忆》。第 1 卷。马德拉斯：穆迪阿尔佩特中学，第 100 页。
  46. Kanigel 1991，第 73 页。
  47. Kanigel 1991，第 74–75 页。
  48. 兰伽纳坦，希亚利·拉玛姆里塔（1967）。《拉马努金：人及其数学》。孟买：亚洲出版公司，第 23 页。ISBN 9788185273372。
  49. 斯里尼瓦桑（1968），第 1 卷，第 99 页。
  50. Rao, K. Srinivasa。“拉马努金的妻子贾纳基亚玛尔（贾纳基）”(PDF)。《金奈数学科学研究所》。原始 PDF 存档于 2017 年 1 月 10 日。检索于 2016 年 9 月 7 日。
  51. “关于拉马努金”。拉马努金研究所。原始页面于 2016 年 10 月 6 日存档。检索于 2016 年 9 月 7 日。
  52. Kanigel 1991，第 77 页。
  53. Srinivasan（1968 年），第 1 卷，第 129 页。
  54. Srinivasan（1968 年），第 1 卷，第 86 页。
  55. Neville, Eric Harold（1921 年 1 月）。“已故斯里尼瓦瑟·拉马努金”。《自然》期刊，第 106 卷（2673 期）：661–662。Bibcode:1921Natur.106..661N。doi:10.1038/106661b0。S2CID 4185656。
  56. Ranganathan 1967，第 24 页。
  57. Kanigel 1991，第 80 页。
  58. Kanigel 1991，第 86 页。
  59. Herschfeld, Aaron（1935 年 8 月）。“关于无限根式”。《美国数学月刊》，第 42 卷（第 7 期）：419–429。doi:10.1080/00029890.1935.11987745。ISSN 0002-9890。
  60. Kanigel 1991，第 87 页。
  61. Kanigel 1991，第 91 页。
  62. Seshu Iyer, P. V.（1920 年 6 月）。“已故 S·拉马努金先生，文学士，英国皇家学会会士”。《印度数学会期刊》，第 12 卷（第 3 期）：第 83 页。
  63. Neville, Eric Harold（1942 年）。“斯里尼瓦瑟·拉马努金”。《自然》期刊，第 149 卷（3776 期）：292–293。Bibcode:1942Natur.149..292N。doi:10.1038/149292a0。
  64. Srinivasan（1968 年），第 176 页。
  65. Srinivasan（1968 年），第 31 页。
  66. Srinivasan（1968 年），第 49 页。
  67. Kanigel 1991，第 96 页。
  68. Berndt 与 Rankin（2001 年），第 97 页。
  69. Kanigel 1991，第 105 页。
  70. M.J.M. 希尔（M. J. M. Hill）致 C. L. T. 格里菲斯（C. L. T. Griffith，曾是学生，他代拉马努金向希尔提出请求）的信，日期：1912 年 11 月 28 日。
  71. Kanigel 1991，第 106 页。
  72. Kanigel 1991，第 170–171 页。
  73. 哈代，G.H.（戈弗雷·哈罗德）（1910 年）《无穷阶（Orders of Infinity）：保罗·杜布瓦-雷蒙德的 “无穷微积分”》。
  74. Bruce C. Berndt 与 Robert A. Rankin（2000 年 8 月），“拉马努金在印度所研读的书籍”，《美国数学月刊》，第 107 卷（第 7 期）：595–601。doi:10.1080/00029890.2000.12005244。ISSN 0002-9890。
  75. 斯诺，C.P.（1966 年）《人物的多样性（Variety of Men）》。纽约：查尔斯·斯克里布纳之子公司。第 30–31 页。
  76. 哈代，G.H.（1920 年）“讣告：S.拉马努金”，《自然》期刊，第 105 卷（第 7 期）：494–495。Bibcode:1920Natur.105..494H。doi:10.1038/105494a0。S2CID 4174904。
  77. Kanigel 1991，第 167 页
  78. Kanigel 1991，第 168 页
  79. 信件：哈代致拉马努金，1913 年 2 月 8 日
  80. 信件：拉马努金致哈代，1914 年 1 月 22 日
  81. Kanigel 1991，第 185 页
  82. 信件：拉马努金致哈代，1913 年 2 月 27 日，藏于剑桥大学图书馆
  83. Kanigel 1991，第 175 页
  84. 拉姆，Suresh（1972 年）《斯里尼瓦瑟·拉马努金》。新德里：国家图书信托，第 29 页
  85. Ranganathan 1967，第 30–31 页
  86. Ranganathan 1967，第 12 页
  87. Kanigel 1991，第 183 页
  88. Kanigel 1991，第 184 页
  89. 《斯里尼瓦瑟·拉马努金的（非常）简短历史》，2021 年 1 月 31 日，已存档于 2021 年 12 月 11 日——通过 YouTube
  90. Berndt 与 Rankin（2001 年），第 83–84 页
  91. Kanigel 1991，第 196 页
  92. 《劳氏船级社登记册 1930 年》（PDF），1930 年，2020 年 9 月 1 日查阅。Nevasa 号，1913 年
  93. Kanigel 1991，第 202 页
  94. Hardy, G. H.（1940 年）《拉马努金》，剑桥：剑桥大学出版社，第 10 页。
  95. 信件：利特尔伍德致哈代，1913 年 3 月初。
  96. Hardy, G. H.（1979 年）《G. H. Hardy 论文集》第七卷，英国牛津：克拉伦登出版社，第 720 页。
  97. 《剑桥大学通报》1916 年 3 月 18 日报道：“艺术学士候选人，斯里尼瓦瑟·拉马努金（研究生），三一学院。” 该文档的清晰照片可在以下 YouTube 视频中指定时间戳处查看：[https://www.youtube.com/watch?v=uhNGCn_3hmc&t=1636](https://www.youtube.com/watch?v=uhNGCn_3hmc&t=1636)
  98. “英国数学博士的历史笔记”。网址：[www.economics.soton.ac.uk。检索日期：2020 年 8 月 9 日。](http://www.economics.soton.ac.uk。检索日期：2020 年 8 月 9 日。)
  99. Jean-Louis Nicolas 和 Guy Robin（编辑），《斯里尼瓦瑟·拉马努金的高度合成数》，《拉马努金期刊》1997 年第 1 卷，第 119–153 页，第 121 页。
  100. Embleton, Ellen（2018 年 10 月 2 日）。“重访拉马努金”。《皇家学会》。原文于 2020 年 2 月 16 日存档。检索于 2020 年 2 月 16 日。
  101. Kanigel 1991，第 299–300 页。
  102. S·钱德拉塞卡，《F.R.S.拉马努金生平中的一则事件：与 G.H.哈代 FRS 及 J.E.利特尔伍德 FRS 的对话及其后续》，论文存放于英国皇家学会（1977 年 8 月 18 日），后重印于：Bruce C. Berndt 和 Robert Alexander Rankin 编，《拉马努金：论文与回顾》，美国数学学会，2001 年，普罗维登斯。
  103. Young, D. A. B.（1994 年）。“拉马努金的疾病”，《伦敦皇家学会笔记与记录》48（1）：107–119，doi:10.1098/rsnr.1994.0009，PMID: 11615274，S2CID: 33416179。
  104. 拉马塞尚，S.，“斯里尼瓦瑟·拉马努金”（1990 年）《当代科学》，第 59 卷第 24 期，1990 年 12 月 25 日，本文为 1987 年 12 月 15 日至 18 日在库姆巴科南举行的 “拉马努金百年国际会议” 上的演讲内容。
  105. Peterson, Doug. “失落笔记的探索者”。伊利诺伊大学厄本那-香槟分校文理学院网站。原文于 2014 年 1 月 12 日存档，检索于 2014 年 1 月 11 日。
  106. Gunn, J. W. C.; Savage, B.（1919 年）。“溶组织内阿米巴感染治疗报告”，《皇家陆军军医杂志》33（5）：418–426。
  107. Langley, George J.（1921 年 12 月 24 日）。“肝脓肿诊断与治疗的困难”，《英国医学杂志》，第 2 卷（3182 期）：1073–1074，doi:10.1136/bmj.2.3182.1073，JSTOR: 20429465，PMC: 2339657，PMID: 20770524。
  108. Baaquie, Belal E.; Willeboordse, Frederick H.（2009 年 12 月 1 日）《综合科学探索》，CRC 出版社，第 38 页，ISBN: 978-1-4200-8794-9。
  109. “拉马努金的个性”，原文于 2007 年 9 月 27 日存档，检索于 2018 年 6 月 23 日。
  110. Kanigel 1991，第 234、241 页。
  111. Kanigel 1991，第 36 页。
  112. Kanigel 1991，第 281 页。
  113. Chaitin, Gregory（2007 年 7 月 28 日）。“少一点证明，多一点真理”，《新科学人》（第 2614 期）：第 49 页，doi:10.1016/S0262-4079(07)61908-3。
  114. Kanigel 1991，第 283 页。
  115. Berndt 与 Rankin 2001，第 47 页。
  116. Berndt, Bruce C.（1989 年）。“斯里尼瓦瑟·拉马努金”，《美国学者》58（2）：234–244，ISSN: 0003-0937，JSTOR: 41211668。
  117. Ranganathan 1967，第 82 页
  118. Calyampudi Radhakrishna Rao（1997 年）《统计与真理：让机遇发挥作用》，世界科技出版社，第 185 页，ISBN 978-981-02-3111-8，检索于 2010 年 6 月 7 日。
  119. Iwaniec, Henryk（1989 年）。“圆法与模形式的傅里叶系数”，载于《数论与相关课题》（1988 年，孟买），塔塔基础研究所数学研究，第 12 卷，塔塔基础研究所，孟买，第 47–55 页，MR 编号：1441326。
  120. “数学家的百年临终梦被证明是真实的”，福克斯新闻，2012 年 12 月 28 日，原文于 2013 年 1 月 7 日存档。
  121. Winnie, Wen-Ching（2019 年 12 月 9 日）。“拉马努金猜想及其应用”，《皇家学会哲学汇刊 A：数学、物理与工程科学》378（2163），doi:10.1098/rsta.2018.0441，PMC：6939229，PMID：31813366。
  122. Ramanujan, Srinivasa（1916 年）。“关于某些算术函数”（PDF），《剑桥哲学会汇刊》，第 22 卷第 9 期，原文（PDF）于 2016 年 6 月 11 日存档，检索于 2016 年 5 月 15 日。τ函数的内容见第 194–197 页。
  123. Ono, Ken；Aczel, Amir D.（2016 年 4 月 13 日）《我寻找拉马努金的旅程：我如何学会计数》，施普林格出版社，第 236–237 页，ISBN 978-3319255668。书中提及的一些思想对于费马大定理的证明具有关键意义。
  124. Berndt, Bruce C.（1997 年 12 月 12 日）《拉马努金笔记》，施普林格出版社，ISBN 978-0387949413。
  125. “哈代语录”。Gap.dcs.st-and.ac.uk，原文于 2012 年 7 月 16 日存档，检索于 2012 年 11 月 20 日。
  126. Hardy, G. H. “讣告：斯里尼瓦瑟·拉马努金”，《伦敦数学会会刊》第 19 卷，第 lvii 页，原文于 2016 年 3 月 5 日存档。
  127. Ross, Greg（2017 年 2 月 6 日）“播客第 140 期：拉马努金”，Futility Closet，检索于 2023 年 12 月 24 日。
  128. James R. Newman（编）（2000 年）《数学的世界》，纽约米尼奥拉：多佛出版公司，第 373–374 页，ISBN 978-0-486-41153-8，OCLC 编号：43555029。
  129. Hardy, G. H.（1937 年 3 月）“印度数学家拉马努金”，《美国数学月刊》44（3）：137–155，doi:10.1080/00029890.1937.11987940，ISSN 0002-9890。
  130. “斯里尼瓦瑟·拉马努金”，原文于 2005 年 3 月 25 日存档，检索于 2010 年 12 月 2 日。
  131. Alyangar, Srinivasa Ramanujan（1995 年），由 Berndt, Bruce C. 和 Rankin, Robert Alexander 编，《拉马努金：书信与评注》，《数学史丛书》第 9 卷，美国数学学会，第 51 页，ISBN 0821891251，检索于 2023 年 2 月 22 日。
  132. Rao, K. Srinivasa. “斯里尼瓦瑟·拉马努金（1887 年 12 月 22 日－1920 年 4 月 26 日）”。原文于 2012 年 4 月 16 日存档。检索于 2018 年 6 月 23 日。
  133. “布鲁斯·伯恩特讲述《拉马努金遗失的笔记》，2011 年 5 月 24 日，印度理工学院马德拉斯分校”。2011 年 5 月 30 日。原文于 2015 年 12 月 6 日存档 —— 来源：YouTube。
  134. “科学先驱日历”，《自然》，第 107 卷（2686 期）：第 252–254 页，1921 年 4 月 21 日。Bibcode:1921Natur.107..252. doi:10.1038/107252b0。
  135. 斯里尼瓦瑟·拉马努金相关邮票。commons.wikimedia.org
  136. “萨斯特拉大学——斯里尼瓦瑟·拉马努金中心——关于我们”。原文于 2017 年 6 月 15 日存档。检索于 2018 年 6 月 23 日。
  137. “辛格首次访问该邦”，CNN IBN，印度，2011 年 12 月 26 日。原文于 2012 年 7 月 15 日存档。检索于 2016 年 4 月 12 日。
  138. “欢迎 2012——印度国家数学年”，印度，2011 年 12 月 28 日。原文于 2017 年 12 月 6 日存档。检索于 2017 年 12 月 6 日。
  139. “拉马努金信息技术城——哈代大楼”。JLL 印度地产。
  140. “《爱上数字的人》”。IMDb，1988 年 3 月 22 日。检索于 2021 年 9 月 24 日。
  141. “戛纳：戴夫·帕特尔将饰演著名印度数学家”。hollywoodreporter.com。原文于 2014 年 1 月 9 日存档。
  142. 巴拉克劳，利奥（2013 年 12 月 5 日）。“杰瑞米·艾恩斯将联袂出演《知无不言的人》”。variety.com。原文于 2017 年 10 月 12 日存档。
  143. 麦克纳里，戴夫（2014 年 7 月 15 日）。“戴夫·帕特尔主演的《知无不言的人》在开发八年后正式开拍”。variety.com。原文于 2017 年 7 月 4 日存档。
  144. “‘拉马努金’剧组在他故居取景拍摄”。《印度时报》。原文于 2013 年 7 月 11 日存档。检索于 2013 年 7 月 12 日。
  145. “樟脑电影公司推出首部作品《拉马努金》”。Box Office India，Select Publishing Company，2013 年 6 月 11 日。原文于 2013 年 8 月 20 日存档。检索于 2013 年 7 月 12 日。
  146. “‘拉马努金’剧组在天才故居拍摄”。Z News，Zee Media Corporation Ltd.。原文于 2013 年 7 月 8 日存档。检索于 2013 年 7 月 12 日。
  147. Krishnamachari, Suganthy（2013 年 6 月 27 日）。“天才的苦难之路”。《印度教报》，印度金奈。原文于 2013 年 7 月 1 日存档。检索于 2013 年 7 月 12 日。
  148. “浦那电影人在国家科学电影节上获得三项大奖”。《印度快报》，2017 年 2 月 27 日。
  149. “拉马努金（重塑 20 世纪数学的人）(2018)”。Indiancine.ma。
  150. Basu, Kankana（2014 年 12 月 7 日）。“快节奏的阅读”。《印度教报》。检索于 2016 年 4 月 30 日。
  151. “高科技世界里的犯罪”。2014 年 9 月 16 日。原文于 2016 年 4 月 15 日存档。检索于 2016 年 4 月 30 日。
  152. Ribet, Kenneth A.（2003 年 12 月）。“剧评：《分割》”（PDF）。《美国数学学会通告》50(1): 1407–1408。原文（PDF）于 2016 年 10 月 6 日存档。检索于 2016 年 9 月 27 日。
  153. Harvey, Dennis（2003 年 5 月 18 日）。“评论：‘分割’”。原文于 2016 年 10 月 6 日存档。检索于 2017 年 3 月 23 日。
  154. “《分割》——一部关于拉马努金的剧作”。《印度教报》，2003 年 5 月 26 日。原文于 2008 年 7 月 20 日存档。
  155. DATTA, SRAVASTI（2014 年 12 月 19 日）。“向一位天才致敬”。《印度教报》。检索于 2017 年 3 月 23 日。
  156. “《头等人》。” Alteregoproductions.org。原文于 2007 年 6 月 29 日存档。检索于 2012 年 11 月 20 日。
  157. “新闻 / 全国：詹姆斯·邦德导演将拍摄拉马努金传记片”。《印度教报》。印度。2011 年 10 月 16 日。原文于 2011 年 10 月 17 日存档。检索于 2011 年 10 月 18 日。
  158. Lunden, Jeff（2010 年 7 月 15 日）。“《消失的数字》：一场生动的戏剧性等式”。《晨间特辑》，美国国家公共电台。检索于 2018 年 4 月 24 日。
  159. Freudenberger, Nell（2007 年 9 月 16 日）。“对数字的渴望”。《纽约时报》。原文于 2012 年 1 月 10 日存档。检索于 2011 年 9 月 4 日。
  160. Taylor, D. J.（2008 年 1 月 26 日）。“构成一个人生”。《卫报》（英国）。原文于 2014 年 10 月 6 日存档。检索于 2011 年 9 月 4 日。
  161. “谷歌为拉马努金诞辰 125 周年发布涂鸦”。《印度时报》，2012 年 12 月 22 日。原文于 2012 年 12 月 22 日存档。检索于 2012 年 12 月 22 日。
  162. “斯里尼瓦瑟·拉马努金诞辰 125 周年纪念”。[www.google.com。原文于 2016 年 5 月 10 日存档。检索于 2016 年 4 月 30 日。](http://www.google.com。原文于 2016 年 5 月 10 日存档。检索于 2016 年 4 月 30 日。)
  163. Kumar, V. Krishna（2018 年 2 月 2 日）。“一位传奇的数学创意天才：斯里尼瓦瑟·拉马努金”。《今日心理学》。检索于 2018 年 4 月 24 日。
  164. Bressoud, David（2006 年）。“书评：《拉马努金的失落笔记，第 I 卷》，作者 George Andrews 与 Bruce C. Berndt”（PDF）。《美国数学会通报（新系列）》第 43 卷第 4 期，第 585–591 页。doi:10.1090/s0273-0979-06-01110-4。原文（PDF）于 2015 年 6 月 23 日存档。
  165. “斯里尼瓦瑟·拉马努金提出的某些积分的一个简单解法”（PDF）。《共鸣》杂志，第 13 卷第 9 期，第 882–884 页。原文（PDF）于 2018 年 10 月 6 日存档。
  166. Bell, E. T.（1928 年）。“《斯里尼瓦瑟·拉马努金论文集》，由 G. H. Hardy、P. V. Seshu Aiyar 与 B. M. Wilson 编辑”。《美国数学会通报》第 34 卷第 6 期，第 783–784 页。doi:10.1090/S0002-9904-1928-04651-7。

19. 外部链接

媒体链接

传记链接

其他链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利