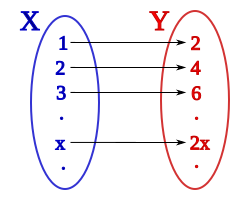可数集（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　 在数学中，如果一个集合是有限的，或者它可以与自然数集合建立一一对应关系，那么它就是可数的。\(^\text{[a]}\) 等价地说，如果存在一个从该集合到自然数的单射函数，那么该集合就是可数的；这意味着集合中的每个元素都可以与一个唯一的自然数对应，或者说集合的元素可以一个接一个地数出来，尽管由于元素个数无限，计数过程可能永远不会结束。

　　 从更技术性的角度讲，假设接受可数选择公理，若一个集合的基数（即集合中的元素个数）不大于自然数集合的基数，则它是可数的。一个可数但不是有限的集合称为可数无穷。

　　 这一概念归功于格奥尔格·康托尔，他证明了不可数集的存在，也就是说存在一些集合不是可数的；例如实数集合就是不可数的。

1. 关于术语的说明

　　 尽管这里所定义的 “可数” 与 “可数无穷” 用法相当普遍，但并非所有文献都采用这种术语。\(^\text{[1]}\) 一种替代用法是：用 countable 来表示这里所说的 “可数无穷”，而用 at most countable 来表示这里所说的 “可数”。\(^\text{[2][3]}\)

　　 术语 enumerable\(^\text{[4]}\) 和 denumerable\(^\text{[5][6]}\) 也可能被使用，例如分别指代 “可数” 和 “可数无穷”。\(^\text{[7]}\) 但其定义并不统一，并且需要注意与 “递归可枚举” 的区别。\(^\text{[8]}\)

2. 定义

　　 一个集合 $S$ 是可数的，当且仅当满足以下任一条件：

• 它的基数 $|S|$ 小于或等于 $\aleph_{0}$（阿列夫零，$\mathbb{N}$ ——自然数集的基数）。\(^\text{[8]}\)
• 存在一个从 $S$ 到 $\mathbb{N}$ 的单射函数。\(^\text{[10][11]}\)
• $S$ 是空集，或者存在一个从 $\mathbb{N}$ 到 $S$ 的满射函数。\(^\text{[11]}\)
• 存在 $S$ 与 $\mathbb{N}$ 的某个子集之间的双射映射。\(^\text{[12]}\)
• $S$ 要么是有限的（$|S| < \aleph_{0}$），要么是可数无穷的。\(^\text{[5]}\)

　　 以上定义都是等价的。

　　 一个集合 $S$ 是可数无穷的，当且仅当：

• 它的基数 $|S|$ 正好等于 $\aleph_{0}$。\(^\text{[9]}\)
• 存在一个从 $S$ 到 $\mathbb{N}$ 的既单射又满射（因此是双射）的映射。
• $S$ 与 $\mathbb{N}$ 之间存在一一对应关系。\(^\text{[13]}\)
• $S$ 的元素可以排列成一个无限序列 $a_{0}, a_{1}, a_{2}, \ldots$ 其中 $a_i \neq a_j$（当 $i \neq j$ 时），并且 $S$ 的每个元素都在该序列中出现。\(^\text{[14][15]}\)

　　 如果一个集合不是可数的，即它的基数大于 $\aleph_{0}$，那么它就是不可数的。[9]

3. 历史

　　 1874 年，康托尔在他的第一篇集合论文章中证明了实数集是不可数的，从而表明并非所有无限集合都是可数的。\(^\text{[16]}\)1878 年，他利用一一对应来定义并比较基数。\(^\text{[17]}\)1883 年，他用无限序数扩展了自然数，并利用序数集合构造出具有不同无限基数的无限多个集合。\(^\text{[18]}\)

4. 引言

　　 集合是元素的一个整体，可以通过多种方式来描述。一种方式就是直接列出所有元素；例如，包含整数 3、4 和 5 的集合可以记作 $\{3, 4, 5\}$，这称为列举法。\(^\text{[19]}\) 然而，这种方法只对小集合有效；对于较大的集合，这会非常耗时且容易出错。为了避免逐一列出所有元素，有时会使用省略号 “...” 来表示从起始元素到结束元素之间的很多元素，前提是作者认为读者能很容易推测出 “...” 所代表的内容。例如：$\{1,2,3,\dots,100\} $ 通常表示从 1 到 100 的所有整数。即便在这种情况下，仍然有可能把所有元素完全列出，因为这个集合中的元素个数是有限的。如果我们依次给集合中的元素编号为 1，2，…，直到 $n$，这就给出了 “大小为 $n$ 的集合” 的通常定义。

　　 有些集合是无限的；这些集合的元素数目大于任意一个可以指定的整数 $n$。（无论指定的整数 $n$ 多大，比如 $n=10^{1000}$，无限集中的元素都比 $n$ 多。）例如，自然数集合可以记作：$\{0,1,2,3,4,5,\dots\}$，它有无穷多个元素，我们无法用任何一个自然数来表示它的大小。\(^\text{[a]}\) 看起来很自然的做法是将集合分为不同的类：把所有只含有一个元素的集合放在一起；所有含有两个元素的集合放在一起；……；最后，把所有无限集合放在一起，并认为它们大小相同。这种观点对于可数无限集是成立的，并且在格奥尔格·康托尔之前是普遍的假设。例如，奇数集合是无限的，偶数集合是无限的，整数集合也是无限的。我们可以认为这些集合大小相同，因为我们可以这样安排：对每一个整数，都对应一个唯一的偶数： $$ \ldots,\,-2 \mapsto -4,\,-1 \mapsto -2,\,0 \mapsto 0,\,1 \mapsto 2,\,2 \mapsto 4,\ldots~ $$ 更一般地：$n \mapsto 2n$（见图）。这里我们所做的是在整数集合与偶数集合之间建立了一一对应（双射）。双射是两个集合之间的一个映射，使得每个集合中的每个元素都唯一对应于另一个集合中的某个元素。这种数学上的 “大小” 概念称为基数：两个集合大小相同，当且仅当它们之间存在双射。所有与整数集合存在一一对应的集合称为可数无穷集，并且它们的基数记作 $\aleph_{0}$。

　　 康托尔证明了并非所有无限集都是可数无穷的。例如，实数集合不能与自然数集合（一切非负整数）建立一一对应关系。实数集的基数大于自然数集，因此称为不可数的。

5. 形式化概述

　　 根据定义，一个集合 $S$ 是**可数的**，如果存在一个 $S$ 与自然数集合 $\mathbb{N}=\{0,1,2,\dots\}$ 的某个子集之间的双射。

　　 例如，定义对应关系： $$ a \leftrightarrow 1, \quad b \leftrightarrow 2, \quad c \leftrightarrow 3~ $$ 由于集合 $S=\{a,b,c\}$ 中的每个元素都恰好与集合 $\{1,2,3\}$ 中的一个元素配对，反之亦然，这就构成了一个双射，并说明 $S$ 是可数的。类似地，我们可以证明所有有限集合都是可数的。

　　 对于无限集合的情况：一个集合 $S$ 是可数无穷的，当且仅当存在一个 $S$ 与整个自然数集合 $\mathbb{N}$ 之间的双射。例如，考虑集合 $A = \{1,2,3,\dots\}$（正整数集合）和 $B = \{0,2,4,6,\dots\}$（偶整数集合）。我们可以通过展示它们与自然数集的双射来说明这些集合是可数无穷的。这可以通过如下映射实现：$n\leftrightarrow n+1, \quad n \leftrightarrow 2n$ 于是： $$ \begin{matrix} 0 \leftrightarrow 1, & 1 \leftrightarrow 2, & 2 \leftrightarrow 3, & 3 \leftrightarrow 4, & 4 \leftrightarrow 5, & \dots \\[6pt] 0 \leftrightarrow 0, & 1 \leftrightarrow 2, & 2 \leftrightarrow 4, & 3 \leftrightarrow 6, & 4 \leftrightarrow 8, & \dots \end{matrix} ~ $$ 这就分别建立了自然数集与正整数集、自然数集与偶整数集之间的一一对应关系，从而说明它们是可数无穷的。

　　 每一个可数无穷集都是可数的，而每一个无限可数集也是可数无穷的。此外，自然数集合的任意子集都是可数的，更一般地：

　　 定理 —— 可数集的子集仍是可数的。\(^\text{[20]}\)

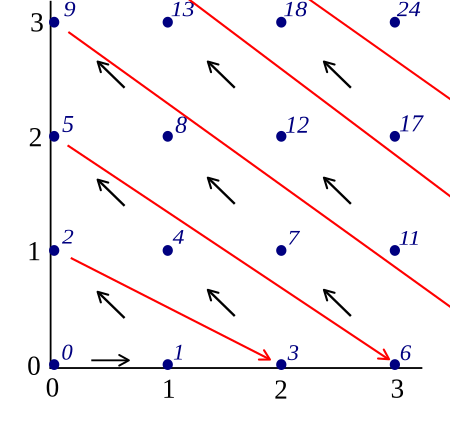
　　 所有自然数有序对的集合（即自然数集合的笛卡尔积 $\mathbb{N} \times \mathbb{N}$）是可数无穷的，这一点可以通过按照图中所示路径进行枚举来说明：

　　 得到的映射过程如下：

　　 $$ 0 \leftrightarrow (0,0),\; 1 \leftrightarrow (1,0),\; 2 \leftrightarrow (0,1),\; 3 \leftrightarrow (2,0),\; 4 \leftrightarrow (1,1),\; 5 \leftrightarrow (0,2),\; 6 \leftrightarrow (3,0),\; \ldots~ $$ 这种映射覆盖了所有这样的有序对。

　　 这种三角形映射的形式可以递归推广到自然数的 $n$-元组，即 $(a_{1}, a_{2}, a_{3}, \dots , a_{n})$，其中 $a_i$ 和 $n$ 都是自然数。方法是不断地将 $n$-元组的前两个元素映射为一个自然数。例如 $(0,2,3)$ 可以写作 $((0,2),3)$。其中，$(0,2)$ 映射为 5，因此 $((0,2),3)$ 映射为 $(5,3)$，然后 $(5,3)$ 映射为 39。由于不同的二元组（例如 $(a,b)$）会映射到不同的自然数，因此只要两个 $n$-元组在某一元素上不同，就能保证它们被映射到不同的自然数。由此证明了从所有 $n$-元组集合到自然数集合 $\mathbb{N}$ 的一个单射存在。对于由有限多个不同集合的笛卡尔积构成的 $n$-元组，每个元组中的每个元素都可以对应到一个自然数，因此每个元组都可以写成自然数形式，然后应用同样的逻辑即可证明该结论。

　　 定理 —— 有限多个可数集合的笛卡尔积仍然是可数的。\(^\text{[21][b]}\)

　　 整数集合 $\mathbb{Z}$ 和有理数集合 $\mathbb{Q}$ 直观上看起来要比自然数集合 $\mathbb{N}$“大得多”。但直觉可能会欺骗我们。如果把一对整数看作是一个普通分数（即形式为 $a/b$ 的分数，其中 $a$ 和 $b\neq 0$ 都是整数）的分子与分母，那么对于每一个正分数，我们都能找到一个与之对应的自然数。这种表示方法同样包含了自然数，因为每个自然数 $n$ 也可以写作分数 $n/1$。因此我们可以得出结论：正有理数的个数与正整数的个数一样多。进一步，这一结论对所有有理数同样成立，具体如下所示。

　　 定理 ——$\mathbb{Z} \quad \text{（整数集合）} \quad \text{与} \quad \mathbb{Q} \quad \text{（有理数集合）}$ 都是可数的。\(^\text{[c]}\)

　　 以类似的方法，代数数集合是可数的。\(^\text{[23][d]}\)

　　 有时候，使用多个映射会更方便：若要证明一个集合 $A$ 是可数的，可以先把 $A$ 单射（即一一映射）到另一个集合 $B$，然后若 $B$ 又能单射到自然数集合，那么就可以推出 $A$ 是可数的。例如，正有理数集合可以很容易地单射到自然数对（即 2 元组）集合，因为分数 $p/q$ 可以映射为有序对 $(p,q)$。而自然数对集合又可以（实际上是一一对应，即双射）映射到自然数集合（如上所示），因此正有理数集合被证明是可数的。

　　 定理 —— 任意有限个可数集合的并集仍然是可数的。\(^\text{[24][25][e]}\)

　　 既然我们已经预见到存在不可数的集合，就会想知道：前面的这个结论是否还能进一步推广？答案既是 “可以”，也是 “不可以”。要扩展这个结论，我们需要额外假设一个新的公理。

　　 定理 ——（假设可数选择公理）可数多个可数集合的并集仍然是可数的。\(^\text{[f]}\)

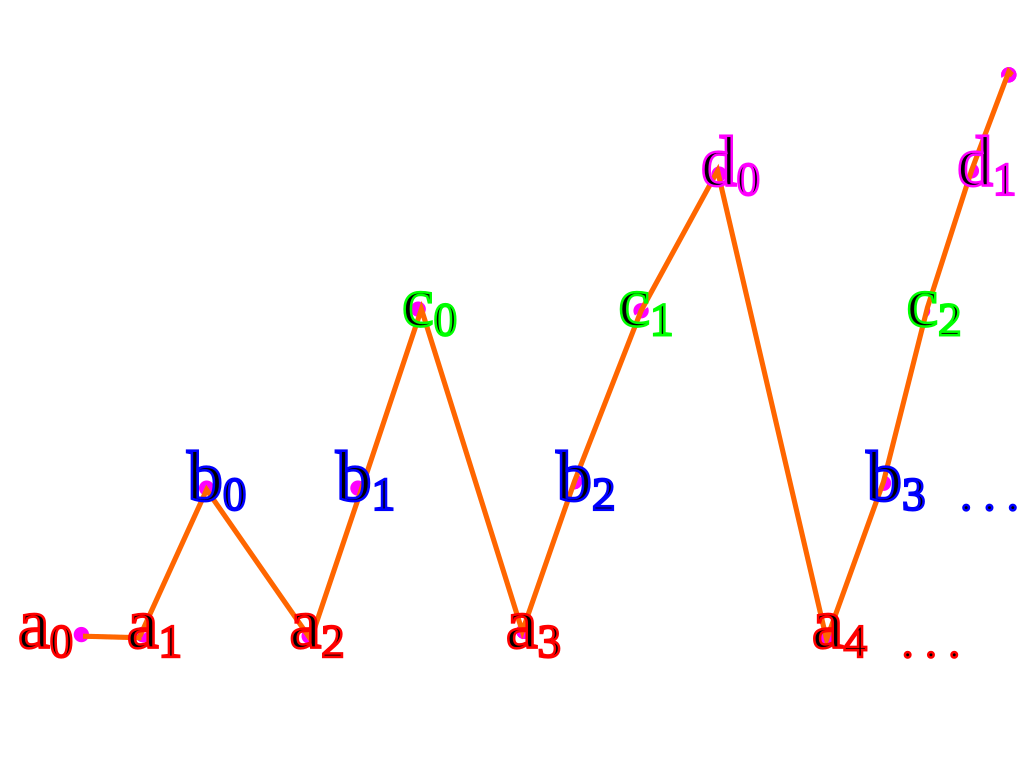
　　 例如，给定若干可数集 $\mathbf{a}, \mathbf{b}, \mathbf{c}, \dots$， 我们首先给每个集合的每个元素分配一个元组，然后再利用前面提到的三角形枚举法的变体为每个元组分配一个索引：

　　 我们需要可数选择公理来同时为所有这些集合 $\mathbf{a}, \mathbf{b}, \mathbf{c}, \dots$ 建立索引。

　　 定理 ——所有有限长度自然数序列的集合是可数的。

　　 这个集合可以看作是长度为 1 的序列集合、长度为 2 的序列集合、长度为 3 的序列集合，依此类推的并集。每一个这样的集合都是可数的（因为它们是有限个自然数的笛卡尔积）。因此，这个集合是可数多个可数集合的并集，由前一个定理可知它是可数的。

　　 定理 ——所有自然数的有限子集的集合是可数的。

　　 任何有限子集的元素都可以排列成一个有限序列。有限序列只有可数多个，因此有限子集也只有可数多个。

　　 定理 ——设 $S$ 与 $T$ 是两个集合。

1. 如果函数 $f : S \to T$ 是单射，并且 $T$ 是可数的，那么 $S$ 也是可数的。
2. 如果函数 $g : S \to T$ 是满射，并且 $S$ 是可数的，那么 $T$ 也是可数的。

　　 这些结论直接来自于 “可数集” 在单射 / 满射函数意义下的定义。\(^\text{[g]}\)

　　 康托尔定理断言：如果 $A$ 是一个集合，而 $\mathcal{P}(A)$ 是它的幂集（即 $A$ 的所有子集所组成的集合），那么不存在一个从 $A$ 到 $\mathcal{P}(A)$ 的满射函数。该定理的证明可见于 “康托尔定理” 条目。由此结合前述基本定理，我们立刻得到：

　　 命题 ——集合 $\mathcal{P}(\mathbb{N})$ 是不可数的，即它是不可数集。

　　 关于这一结果的详细阐述，可参见康托尔对角线论证。

　　 实数集是不可数的，\(^\text{[h]}\) 自然数的所有无限序列集合也是不可数的。

6. 集合论的极小模型是可数的

　　 如果存在一个集合，它是 ZFC 集合论的标准模型（参见内模型），那么就存在一个极小标准模型（参见可构造宇宙）。利用 Löwenheim–Skolem 定理可以证明，这个极小模型是可数的。然而，“不可数性” 这一概念即便在该模型中依然有意义。特别是，这个模型 $M$ 中包含一些元素，它们是：

• 作为 $M$ 的子集，因此是可数的；
• 但从 $M$ 的观点来看，却是不可数的。

　　 在集合论发展的早期，这被视为一种悖论；详见 Skolem 悖论。

　　 极小标准模型包含了所有的代数数和所有有效可计算的超越数，以及许多其他类型的数。

7. 全序

　　 可数集可以通过多种方式加上全序，例如：

• 良序（Well-orders，参见序数）：
• 自然数的通常次序 $(0, 1, 2, 3, 4, 5, \dots)$
• 整数的次序 $(0, 1, 2, 3, \dots; -1, -2, -3, \dots)$
• 其他（非良序，Not well orders）：
• 整数的通常次序 $(\dots, -3, -2, -1, 0, 1, 2, 3, \dots)$
• 有理数的通常次序（无法明确地写成一个有序列表！）

　　 在这两个良序的例子中，任意子集都存在最小元素；而在这两个非良序的例子中，有些子集并不存在最小元素。这正是区分一个全序是否为良序的关键定义。

8. 参见

• 阿列夫数
• 计数
• 希尔伯特旅馆悖论
• 不可数集

9. 注释

　　
a.由于 $\mathbb{N}$ 与 $\mathbb{N}^{*}=\{1,2,3,\dots\}$ 之间存在显然的双射，所以是否将 0 视为自然数并无区别。无论如何，本文遵循 ISO 31-11 和数学逻辑中的标准约定，即把 0 视为自然数。
b.证明：注意到 $\mathbb{N} \times \mathbb{N}$ 是可数的，这直接来自定义，因为函数 $f : \mathbb{N} \times \mathbb{N} \to \mathbb{N}, \quad f(m,n) = 2^{m}\cdot 3^{n}$ 是单射。[22]于是可以推出，任意两个可数集合的笛卡尔积都是可数的。事实上，如果 $A$ 和 $B$ 是两个可数集，那么存在满射 $ f : \mathbb{N} \to A, \quad g : \mathbb{N} \to B$。因此，映射 $f \times g : \mathbb{N} \times \mathbb{N} \to A \times B$ 是从可数集 $\mathbb{N} \times \mathbb{N}$ 到集合 $A \times B$ 的一个满射。由推论可得，$A \times B$ 是可数的。这一结果可以推广到有限多个可数集合的笛卡尔积，证明可以通过对集合数量作归纳而得。
c.证明：整数集 $\mathbb{Z}$ 是可数的，因为函数 $$ f : \mathbb{Z} \to \mathbb{N}, \quad f(n) = \begin{cases} 2^{n}, & n \geq 0 \\[6pt] 3^{-n}, & n < 0 \end{cases}~ $$ 是一个单射函数。有理数集 $\mathbb{Q}$ 是可数的，因为函数 $g : \mathbb{Z} \times \mathbb{N} \to \mathbb{Q}, \quad g(m,n) = \frac{m}{n+1}$ 是从可数集 $\mathbb{Z} \times \mathbb{N}$ 到有理数集 $\mathbb{Q}$ 的一个满射。
d.证明：根据定义，每个代数数（包括复数）都是某个整系数多项式的根。给定一个代数数 $\alpha$，设 $a_{0}x^{0} + a_{1}x^{1} + a_{2}x^{2} + \cdots + a_{n}x^{n}$ 是一个整系数多项式，并且 $\alpha$ 是该多项式的第 $k$ 个根（其中根按模的大小从小到大排序，再按辐角从小到大排序）。我们可以定义一个单射（即一一）函数 $f : \mathbb{A} \to \mathbb{Q}$,其中 $$ f(\alpha) = 2^{k-1} \cdot 3^{a_{0}} \cdot 5^{a_{1}} \cdot 7^{a_{2}} \cdots {p_{n+2}}^{a_{n}},~ $$ 这里 $p_{n}$ 表示第 $n$ 个质数。
e.证明：如果对每个 $i \in I = \{1, \dots , n\}$，集合 $A_i$ 都是可数的，那么对每个 $i$ 都存在一个满射函数 $g_i : \mathbb{N} \to A_i$.于是我们可以定义函数 $$ G : I \times \mathbb{N} \to \bigcup_{i \in I} A_i, \quad G(i,m) = g_i(m)~ $$ 它是一个满射。由于 $I \times \mathbb{N}$ 是可数的，所以并集 $\bigcup_{i \in I} A_i$ 也是可数的。
f.证明：与有限情形类似，但这里 $I = \mathbb{N}$。我们使用可数选择公理，为每个 $i \in \mathbb{N}$ 选择一个满射 $g_i$，该满射来自于从 $\mathbb{N}$ 到 $A_i$ 的非空满射集合。[26]注意，由于我们考虑的是满射 $$ G : \mathbb{N} \times \mathbb{N} \to \bigcup_{i \in I} A_i~ $$ 而不是单射，因此并不要求这些集合两两不交。
g.证明：(1) 注意，如果 $T$ 是可数的，那么存在一个单射函数 $h : T \to \mathbb{N}$,若 $f : S \to T$ 是单射，则复合函数 $h \circ f : S \to \mathbb{N}$ 也是单射，因此 $S$ 是可数的。(2) 注意，如果 $S$ 是可数的，那么要么 $S$ 是空集，要么存在一个满射函数 $h : \mathbb{N} \to S$.若 $g : S \to T$ 是满射，则要么 $S$ 与 $T$ 都是空集，要么复合函数 $g \circ h : \mathbb{N} \to T$ 是满射。在任一情况下，$T$ 都是可数的。
h.参见**康托尔的第一个不可数性证明，以及有限交性质 # 应用中的拓扑学证明。

10. 引文

1. Manetti, Marco (2015 年 6 月 19 日). *Topology*. Springer. p. 26. ISBN 978-3-319-16958-3.
2. Rudin 1976, 第 2 章
3. Tao 2016, p. 181
4. Kamke 1950, p. 2
5. Lang 1993, 第 I 章 §2
6. Apostol 1969, p. 23, 第 1.14 节
7. Thierry, Vialar (2017 年 4 月 4 日). *Handbook of Mathematics. BoD - Books on Demand. p. 24. ISBN 978-2-9551990-1-5.
8. Mukherjee, Subir Kumar (2009). *First Course in Real Analysis. Academic Publishers. p. 22. ISBN 978-81-89781-90-3.
9. Yaqub, Aladdin M. (2014 年 10 月 24 日). *An Introduction to Metalogic. Broadview Press. ISBN 978-1-4604-0244-3.
10. Singh, Tej Bahadur (2019 年 5 月 17 日). *Introduction to Topology. Springer. p. 422. ISBN 978-981-13-6954-4.
11. Katzourakis, Nikolaos; Varvaruca, Eugen (2018 年 1 月 2 日). *An Illustrative Introduction to Modern Analysis*. CRC Press. ISBN 978-1-351-76532-9.
12. Halmos 1960, p. 91
13. Kamke 1950, p. 2
14. Dlab, Vlastimil; Williams, Kenneth S. (2020 年 6 月 9 日). Invitation To Algebra: A Resource Compendium For Teachers, Advanced Undergraduate Students And Graduate Students In Mathematics. World Scientific. p. 8. ISBN 978-981-12-1999-3.
15. Tao 2016, p. 182
16. Stillwell, John C. (2010). Roads to Infinity: The Mathematics of Truth and Proof. CRC Press. p. 10. ISBN 9781439865507. —— 康托尔在 1874 年发现不可数集，这是数学史上最出乎意料的事件之一。在 1874 年之前，大多数人甚至不认为无穷是一个合法的数学主题，因此无法想象有区分 “可数无穷” 和 “不可数无穷” 的必要。
17. Cantor 1878, p. 242.
18. Ferreirós 2007, pp. 268, 272–273.
19. "What Are Sets and Roster Form?". expii. 2021-05-09. 存档于 2020-09-18.
20. Halmos 1960, p. 91
21. Halmos 1960, p. 92
22. Avelsgaard 1990, p. 182
23. Kamke 1950, pp. 3–4
24. Avelsgaard 1990, p. 180
25. Fletcher & Patty 1988, p. 187
26. Hrbacek, Karel; Jech, Thomas (1999 年 6 月 22 日). Introduction to Set Theory*, 第三版, 修订与扩展版. CRC Press. p. 141. ISBN 978-0-8247-7915-3.

11. 参考文献

• Apostol, Tom M. (1969 年 6 月), Multi-Variable Calculus and Linear Algebra with Applications, 卷 2 (第 2 版), 纽约: John Wiley + Sons, ISBN 978-0-471-00007-5.
• Avelsgaard, Carol (1990), Foundations for Advanced Mathematics, Scott, Foresman and Company, ISBN 0-673-38152-8.
• Cantor, Georg (1878), “Ein Beitrag zur Mannigfaltigkeitslehre”, Journal für die Reine und Angewandte Mathematik, 1878 (84): 242–248, doi:10.1515/crelle-1878-18788413, S2CID 123695365.
• Ferreirós, José (2007), Labyrinth of Thought: A History of Set Theory and Its Role in Mathematical Thought (第 2 次修订版), Birkhäuser, ISBN 978-3-7643-8349-7.
• Fletcher, Peter; Patty, C. Wayne (1988), Foundations of Higher Mathematics, 波士顿: PWS-KENT Publishing Company, ISBN 0-87150-164-3.
• Halmos, Paul R. (1960), *Naive Set Theory*, D. Van Nostrand Company, Inc. 1974 年由 Springer-Verlag, New York 再版, ISBN 0-387-90092-6（Springer-Verlag 版）; 2011 年由 Martino Fine Books 再版, ISBN 978-1-61427-131-4（平装版）.
• Kamke, Erich (1950), Theory of Sets, Dover 数学与物理丛书, 纽约: Dover, ISBN 978-0486601410.
• Lang, Serge (1993), Real and Functional Analysis, 柏林, 纽约: Springer-Verlag, ISBN 0-387-94001-4.
• Rudin, Walter (1976), Principles of Mathematical Analysis, 纽约: McGraw-Hill, ISBN 0-07-054235-X.
• Tao, Terence (2016), “Infinite sets”. Analysis I. Texts and Readings in Mathematics. 卷 37 (第 3 版), 新加坡: Springer, pp. 181–210, doi:10.1007/978-981-10-1789-6_8. ISBN 978-981-10-1789-6.