完整群（综述）

贡献者：待更新

　　本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

图 1：球面上沿分段光滑路径的平行移动。初始向量标记为

V

，它沿着曲线被平行移动，最终得到的向量标记为

P_{γ} (V)

。如果路径发生变化，平行移动的结果也会不同。

　　在微分几何中，光滑流形上一个联络的平行迁移群（holonomy）描述的是：沿着闭合回路进行平行移动时，几何数据未被保持的程度。平行迁移群是联络曲率所导致的一种普遍几何效应。对于平坦联络，相关的平行迁移群是一种单值延拓（monodromy），并且本质上是一个全局概念。而对于曲率非零的联络，平行迁移群同时具有非平凡的局部和全局特征。

　　任何流形上的联络都会通过其平行移动映射引出某种平行迁移群（holonomy）的概念。最常见的平行迁移群形式是具有某种对称性的联络。重要的例子包括：黎曼几何中 Levi-Civita 联络的平行迁移群（称为黎曼平行迁移群），向量丛上联络的平行迁移群，Cartan 联络的平行迁移群，以及主丛上联络的平行迁移群。在这些情形下，联络的平行迁移群都可以与某个李群（即平行迁移群）对应起来。根据 Ambrose-Singer 定理，联络的平行迁移群与该联络的曲率密切相关。

　　对黎曼平行迁移群（Riemannian holonomy）的研究推动了许多重要的发展。平行迁移群最早由埃利·嘉当（Élie Cartan）于 1926 年引入，用于研究和分类对称空间。然而，直到很久之后，平行迁移群才被用来在更一般的背景下研究黎曼几何。

　　 1952 年，乔治·德拉姆（Georges de Rham）证明了德拉姆分解定理，该定理通过将切丛分解为在局部平行迁移群作用下的不可约子空间，从而将黎曼流形分解为多个黎曼流形的笛卡尔积。随后在 1953 年，马塞尔·贝尔热（Marcel Berger）对可能出现的不可约平行迁移群进行了分类。

　　黎曼平行迁移群的分解和分类在物理学和弦理论中都有应用。

1. 定义

向量丛上联络的平行迁移群

　　设 $E$ 是光滑流形 $M$ 上的一个秩为 $k$ 的向量丛， $\nabla$ 是 $E$ 上的一个联络。对于一个以 $M$ 中点 $x$ 为基点的分段光滑闭合路径 $γ : [0, 1] \to M$ ，联络 $\nabla$ 定义了一个平行移动映射 $P_{γ} : E_{x} \to E_{x}$ 它作用在 $E$ 在点 $x$ 处的纤维上。这个映射是线性的且可逆的，因此它定义了一个属于一般线性群 $G L (E_{x})$ 的元素。联络 $\nabla$ 在基点 $x$ 处的平行迁移群（holonomy group）定义为： ${Hol}_{x} (\nabla) = {P_{γ} \in GL (E_{x}) ∣ γ 是以 x 为基点的闭合路径} .$ 其中 $P_{γ}$ 是路径 $γ$ 对应的平行移动映射。基点 $x$ 处的限制平行迁移群（restricted holonomy group）是子群： ${Hol}_{x}^{0} (\nabla)$ 它由可缩至点的闭合路径 $γ$ 所对应的平行移动映射组成。

　　如果 $M$ 是连通的，那么平行迁移群（holonomy group）对于基点 $x$ 的依赖仅体现在一般线性群 $G L (k, R)$ 中的共轭关系上。具体来说，如果 $γ$ 是从 $x$ 到 $y$ 的一条路径，那么： ${Hol}_{y} (\nabla) = P_{γ} {Hol}_{x} (\nabla) P_{γ}^{- 1} .$ 此外，选择不同的方式将纤维 $E_{x}$ 与 $R^{k}$ 进行同构，也会得到共轭的子群。

　　因此，有时，特别是在一般性的或非正式的讨论中（比如下面的内容），人们会省略对基点的引用，此时默认该定义仅确定到共轭的意义下。

　　关于平行迁移群（holonomy group），以下是一些重要性质：

${Hol}^{0} (\nabla)$ 是 $G L (k, R)$ 的一个连通的李子群。
${Hol}^{0} (\nabla)$ 是 $Hol (\nabla)$ 的单位连通分量（identity component）。
存在一个从基本群 $π_{1} (M)$ 到商群 $Hol (\nabla) / {Hol}^{0} (\nabla)$ 的自然满群同态： $π_{1} (M) \to Hol (\nabla) / {Hol}^{0} (\nabla)$ 其中 $π_{1} (M)$ 是 $M$ 的基本群，该同态将同伦类 $[γ]$ 映射为： $P_{γ} \cdot {Hol}^{0} (\nabla)$ .
如果 $M$ 是单连通的，则： $Hol (\nabla) = {Hol}^{0} (\nabla)$ .
当且仅当 $\nabla$ 是平坦的（即曲率为零）， ${Hol}^{0} (\nabla)$ 是平凡群（只包含单位元）。

主丛上联络的平行迁移群

　　主丛上联络的平行迁移群的定义与向量丛上的定义类似。

　　设 $G$ 是一个李群， $P$ 是一个在光滑流形 $M$ 上的主 $G$ -丛，并且 $M$ 是可度量紧化的（paracompact）。设 $ω$ 是 $P$ 上的一个联络。

　　给定一条以 $M$ 中点 $x$ 为基点的分段光滑闭合路径 $γ : [0, 1] \to M$ ，以及纤维上点 $p \in P_{x}$ （ $p$ 属于 $x$ 处的纤维），该联络定义了一条唯一的水平提升路径： $\tilde{γ} : [0, 1] \to P$ 满足： $\tilde{γ} (0) = p$ .这条提升路径的终点 $\tilde{γ} (1)$ 一般不会等于 $p$ ，而是纤维中某个形如 $p \cdot g$ 的点，其中 $g \in G$ 。

　　在 $P$ 上定义一个等价关系 “ $\sim$ ”，规定 $p \sim q$ 当且仅当 $p$ 和 $q$ 可以通过一条分段光滑的水平路径连接。

　　 $ω$ 在基点 $p$ 处的平行迁移群（holonomy group）定义为： ${Hol}_{p} (ω) = {g \in G ∣ p \sim p \cdot g} .$ 基点 $p$ 处的限制平行迁移群（restricted holonomy group）是子群 ${Hol}_{p}^{0} (ω)$ ，它由可缩闭合路径 $γ$ 的水平提升所产生。

　　如果 $M$ 和 $P$ 都是连通的，那么平行迁移群对于基点 $p$ 的依赖仅表现为在 $G$ 中的共轭。具体来说，如果 $q$ 是平行迁移群选取的另一个基点，则存在唯一的 $g \in G$ ，使得： $q \sim p \cdot g$ 在这个 $g$ 下，有： ${Hol}_{q} (ω) = g^{- 1} {Hol}_{p} (ω) g$ 特别地： ${Hol}_{p \cdot g} (ω) = g^{- 1} {Hol}_{p} (ω) g$ 此外，如果 $p \sim q$ ，则有： ${Hol}_{p} (ω) = {Hol}_{q} (ω)$ 与前面类似，有时在讨论平行迁移群时会省略基点的标注，此时默认该定义只在共轭的意义下成立。

　　关于平行迁移群和限制平行迁移群的一些重要性质包括：

${Hol}_{p}^{0} (ω)$ 是李群 $G$ 的一个连通李子群。
${Hol}_{p}^{0} (ω)$ 是 ${Hol}_{p} (ω)$ 的单位连通分量。
存在一个从基本群 $π_{1}$ 到商群 ${Hol}_{p} (ω) / {Hol}_{p}^{0} (ω)$ 的自然的满群同态： $π_{1} \to {Hol}_{p} (ω) / {Hol}_{p}^{0} (ω)$
如果 $M$ 是单连通的，那么： ${Hol}_{p} (ω) = {Hol}_{p}^{0} (ω)$
$ω$ 是平坦的（即曲率为零）当且仅当： ${Hol}_{p}^{0} (ω)$ 是平凡子群（只包含单位元）。

平行迁移丛

　　设 $M$ 是连通的、可度量紧化的光滑流形， $P$ 是一个主 $G$ -丛，并带有如前所述的联络 $ω$ 。取 $p \in P$ 为主丛中的任意一点，定义 $H (p)$ 为可以通过水平曲线连接到 $p$ 的所有点的集合。可以证明， $H (p)$ 配上自然的投影映射，是一个以 ${Hol}_{p} (ω)$ 为结构群的主丛。这个主丛称为联络 $ω$ 的平行迁移丛（holonomy bundle）（通过点 $p$ ）。联络 $ω$ 可以限制为 $H (p)$ 上的一个联络，因为平行移动映射保持 $H (p)$ 内部的点。因此， $H (p)$ 是该联络的一个约化子丛（reduced bundle）。此外，由于不存在比 $H (p)$ 更小的子丛同时能被平行移动保持，因此 $H (p)$ 是这样的最小约化子丛。

　　与平行迁移群一样，平行迁移丛在环境主丛 $P$ 内也会协变变换。具体来说，如果 $q \in P$ 是为平行迁移选择的另一个基点，则存在唯一的 $g \in G$ ，使得 $q \sim p \cdot g$ （因为根据假设， $M$ 是路径连通的）。因此， $H (q) = H (p) \cdot g$ 。由此可得，对于不同基点选择所对应的平行迁移丛，它们上的诱导联络是相容的：它们的平行迁移映射将精确地相差同一个元素 $g$ 。

单调群

　　平行迁移丛 $H (p)$ 是一个主丛，结构群为 ${Hol}_{p} (ω)$ ，因此也承载了限制平行迁移群 ${Hol}_{p}^{0} (ω)$ 的作用（这是完整平行迁移群的正规子群）。离散群 ${Hol}_{p} (ω) / {Hol}_{p}^{0} (ω)$ 被称为该联络的单调群（monodromy group）；它作用于商丛 $H (p) / {Hol}_{p}^{0} (ω)$ 。

　　存在一个满射同态映射 $φ : π_{1} \to {Hol}_{p} (ω) / {Hol}_{p}^{0} (ω)$ ，使得 $φ (π_{1} (M))$ 作用于商丛 $H (p) / {Hol}_{p}^{0} (ω)$ 。

　　这个基本群的作用是基本群的单调表示。

局部和平行迁移的微分形式

　　如果 $π : P \to M$ 是一个主丛，并且 $ω$ 是在 $P$ 上的联络，那么 $ω$ 的平行迁移可以限制在 $M$ 上某个开子集的纤维上。事实上，如果 $U$ 是 $M$ 上的一个连通开子集，那么 $ω$ 限制到 $U$ 上将给出在丛 $π^{- 1} (U)$ 上的联络。这个丛的平行迁移（分别是限制平行迁移）将被记作： ${Hol}_{p} (ω, U) (平行迁移), {Hol}_{p}^{0} (ω, U) (限制平行迁移),$ 对于每个 $p$ ，使得 $π (p) \in U$ 。

　　如果 $U \subset V$ 是两个包含 $π (p)$ 的开集，则有一个显然的包含关系： ${Hol}_{p}^{0} (ω, U) \subset {Hol}_{p}^{0} (ω, V) .$ 在点 $p$ 处的局部平行迁移群定义为： ${Hol}^{*} (ω) = ⋂_{k = 1}^{\infty} {Hol}_{p}^{0} (ω, U_{k})$ 对于任何一族嵌套的连通开集 $U_{k}$ ，满足： $⋂_{k} U_{k} = π (p)$ .

　　局部平行迁移群具有以下性质：

它是受限平行迁移群 ${Hol}_{p}^{0} (ω)$ 的一个连通李子群。
每个点 $p$ 都有一个邻域 $V$ ，使得 ${Hol}_{p}^{*} (ω) = {Hol}_{p}^{0} (ω, V)$ .特别地，局部平行迁移群仅依赖于点 $p$ ，而不依赖于定义它所使用的嵌套开集序列 $U_{k}$ 。
局部平行迁移是关于结构群 $G$ 的元素的平移等变的；即， ${Hol}_{p g}^{*} (ω) = Ad (g^{- 1}) {Hol}_{p}^{*} (ω)$ 对于所有 $g \in G$ 。（注意，依据性质 1，局部平行迁移群是 $G$ 的一个连通李子群，因此伴随作用是良定义的。）

　　局部平行迁移群作为一个全局对象的行为并不好。特别地，它的维数可能不是恒定的。然而，以下定理是成立的：

　　如果局部平行迁移群的维数是恒定的，那么局部平行迁移群和受限平行迁移群相等： ${Hol}_{p}^{*} (ω) = {Hol}_{p}^{0} (ω)$ .

2. 安布罗斯–辛格定理

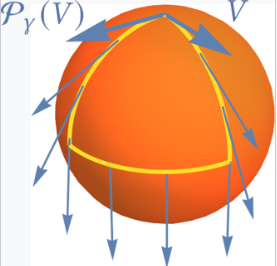
　　安布罗斯–辛格定理（由沃伦·安布罗斯和伊萨多尔·M·辛格（1953 年）提出）将主束中的连接的平行迁移与连接的曲率形式联系起来。为了使这个定理显得合理，可以考虑一个熟悉的情况，即仿射连接（或切丛中的连接——例如，勒维-奇维塔连接）。当沿着一个无穷小的平行四边形行进时，曲率就会出现。

　　详细来说，如果 σ: [0, 1] × [0, 1] → M 是一个在 M 中由一对变量 x 和 y 参数化的曲面，那么一个向量 V 可以沿着 σ 的边界进行平行迁移：首先沿着 (x, 0) 方向，然后沿着 (1, y)，接着沿着 (x, 1) 方向以负方向行进，最后沿着 (0, y) 返回到原点。这是一个平行迁移回路的特例：向量 V 受对应于 σ 边界提升的平行迁移群元素的作用。当平行四边形收缩到零时，曲率显式地出现，通过沿 [0, x] × [0, y] 区域遍历更小的平行四边形的边界。这对应于在 x = y = 0 时对平行迁移映射求导： $\frac{D}{d x} \frac{D}{d y} V - \frac{D}{d y} \frac{D}{d x} V = R (\frac{\partial σ}{\partial x}, \frac{\partial σ}{\partial y}) V$ 其中， $R$ 是曲率张量。[3] 所以，粗略地说，曲率给出了封闭回路（即无穷小平行四边形）上的无穷小平行迁移。更正式地，曲率是平行迁移群在单位元处作用的微分。换句话说， $R (X, Y)$ 是平行迁移群 ${Hol}_{p} (ω)$ 的李代数的一个元素。

　　一般地，考虑一个主丛 $P \to M$ 上的联络的平行迁移，其中主丛的结构群为 $G$ 。令 $g$ 表示 $G$ 的李代数，联络的曲率形式是一个值域为 $g$ 的 2-形式 $Ω$ 定义在 $P$ 上。Ambrose–Singer 定理指出：[4]

　　平行迁移群 ${Hol}_{p} (ω)$ 的李代数由所有形如 $Ω_{q} (X, Y)$ 的 $g$ 元素所张成，其中 $q$ 取遍所有能够通过水平曲线与 $p$ 连通的点（即 $q \sim p$ ），而 $X$ 和 $Y$ 是 $q$ 处的水平切向量。

　　或者，该定理可以用平行迁移丛的语言重新表述：[5]

　　平行迁移群 ${Hol}_{p} (ω)$ 的李代数是李代数 $g$ 的子空间，由形如 $Ω_{q} (X, Y)$ 的元素所张成，其中 $q \in H (p)$ ，而 $X$ 和 $Y$ 是 $q$ 处的水平向量。

3. 黎曼平行迁移

　　黎曼流形的平行迁移是指黎曼流形 $(M, g)$ 上切丛的 Levi-Civita 连接的平行迁移群。一个 “典型的” $n$ -维黎曼流形具有 $O (n)$ 的平行迁移群，若流形是可定向的，则平行迁移群为 $S O (n)$ 。如果流形的平行迁移群是 $O (n)$ 或 $S O (n)$ 的真子群，则该流形具有特殊的性质。

　　关于黎曼平行迁移的早期基本结果之一是 Borel 和 Lichnerowicz（1952）的定理，该定理断言限制的平行迁移群是 $O (n)$ 的闭李子群。特别地，它是紧致的。

可约平行迁移与 de Rham 分解

　　设 $x \in M$ 为任意一点。则平行迁移群 $Hol (M)$ 在切空间 $T_{x} M$ 上作用。这个作用可以是不可约的（作为群表示），也可以是可约的，即存在一个将 $T_{x} M$ 分解为正交子空间 $T_{x} M = T_{x}^{'} M \oplus T_{x}^{″} M$ 的分裂，其中每个子空间在 $Hol (M)$ 的作用下是不变的。在后一种情况下，称 $M$ 为可约的。

　　假设 $M$ 是一个可约流形。让点 $x$ 变化，经过平行迁移群作用下的切空间的分解得到的束 $T^{'} M$ 和 $T^{″} M$ 是光滑的分布，并且在 Frobenius 意义下是可积的。这些分布的积分流形是全测地子流形。因此， $M$ 在局部上是 $M^{'} \times M^{″}$ 的笛卡尔积。局部的 de Rham 同构通过继续这一过程，直到完成切空间的完全分解为止：

　　设 $M$ 是一个简单连通的黎曼流形，[7]让 $T M = T^{(0)} M \oplus T^{(1)} M \oplus \dots \oplus T^{(k)} M$ 是切丛在平行迁移群作用下的完全分解。假设 $T^{(0)} M$ 由在平行迁移群作用下不变的向量组成（即，平行迁移表示是平凡的）。则局部上， $M$ 是等距于一个积式流形： $V_{0} \times V_{1} \times \dots \times V_{k}$ 其中 $V_{0}$ 是欧几里得空间中的开集，且每个 $V_{i}$ 是 $T^{(i)} M$ 的积分流形。此外， $H o l (M)$ 分解为每个 $M_{i}$ 的平行迁移群的直积，其中 $M_{i}$ 是通过某点的 $T^{(i)}$ 的最大积分流形。

　　如果进一步假设 $M$ 是测地完全的，则该定理在全局上成立，并且每个 $M_{i}$ 都是测地完全的流形。[8]

贝尔杰分类

　　 1955 年，M. Berger 给出了对简单连通的不可约（非局部积空间）和非对称（非局部黎曼对称空间）黎曼流形的可能平行迁移群的完整分类。贝尔杰的分类如下：

表1：

$H o l (g)$	$d i m (M)$	流形类型	备注
$S O (n)$	$n$	可定向流形	—
$U (n)$	$2 n$	凯勒流形	凯勒
$S U (n)$	$2 n$	卡拉比–丘流形	黎曼曲率平坦，凯勒
$S p (n) \cdot S p (1)$	$4 n$	四元数–凯勒流形	爱因斯坦
$S p (n)$	$4 n$	超凯勒流形	黎曼曲率平坦，凯勒
$G_{2}$	7	$G_{2}$ 流形	黎曼曲率平坦
$S p i n (7)$	8	$S p i n (7)$ 流形	黎曼曲率平坦

　　具有 $S p (n) \cdot S p (1)$ 作为全局对称性的流形在 1965 年由 Edmond Bonan 和 Vivian Yoh Kraines 同时研究，他们都发现这些流形必然携带一个平行的 4-形式。

　　具有 $G_{2}$ 或 $S p i n (7)$ 作为全局对称性的流形最早由 Edmond Bonan 在 1966 年进行抽象研究，他对这些流形所携带的平行微分形式进行了分类，并证明这类流形必然是黎曼曲率平坦的。然而，直到 30 年后，才实际构造出这样的流形的例子。

　　伯杰的原始列表还包括了 $S p i n (9)$ 作为 $S O (16)$ 的子群的可能性。具有这种全局对称性的黎曼流形后来由 D. Alekseevski 和 Brown-Gray 独立证明，必然是局部对称的，即局部同构于 Cayley 平面 $F_{4} / S p i n (9)$ 或局部平坦的。（见下文。）现在已知所有这些可能性都出现在黎曼流形的全局对称群中。最后两个例外情况是最难找到的。请参见 G2 流形和 Spin(7) 流形。

　　请注意， $S p (n) \subset S U (2 n) \subset U (2 n) \subset S O (4 n)$ ，因此每个超凯勒流形都是 Calabi–Yau 流形，每个 Calabi–Yau 流形都是凯勒流形，而每个凯勒流形都是可定向的。

　　上面的奇异列表通过 Simons 对伯杰定理的证明得到了说明。Carlos E. Olmos 在 2005 年给出了伯杰定理的一个简单且几何的证明。首先可以证明，如果一个黎曼流形不是局部对称空间，并且约简的全等群在切空间上是不可约作用的，那么它会在单位球面上起到遍历作用。已知作用在球面上的李群包括上述列表中的群，并且还有两个额外的情况：一个是 Spin(9) 群作用于 $R^{16}$ ，另一个是群 $T \cdot S p (m)$ 作用于 $R^{4 m}$ 。最后，检查这两个额外情况中的第一个只会作为局部对称空间的全等群出现（这些空间是局部同构于 Cayley 投影平面），而第二个根本不作为全等群出现。

　　上面的奇异列表通过 Simons 对伯杰定理的证明得到了说明。Carlos E. Olmos 在 2005 年给出了伯杰定理的一个简单且几何的证明。首先可以证明，如果一个黎曼流形不是局部对称空间，并且约简的全等群在切空间上是不可约作用的，那么它会在单位球面上起到遍历作用。已知作用在球面上的李群包括上述列表中的群，并且还有两个额外的情况：一个是 $S p i n (9)$ 群作用于 $R^{16}$ ，另一个是群 $T \cdot S p (m)$ 作用于 $R^{4 m}$ 。最后，检查这两个额外情况中的第一个只会作为局部对称空间的全等群出现（这些空间是局部同构于 Cayley 投影平面），而第二个根本不作为全等群出现。

　　伯杰的原始分类还包括了非正定伪黎曼度量的非局部对称全等群。这份列表包括具有 $(p, q)$ 签名的 $S O (p, q)$ ，具有 $(2 p, 2 q)$ 签名的 $U (p, q)$ 和 $S U (p, q)$ ，具有 $(4 p, 4 q)$ 签名的 $S p (p, q)$ 和 $S p (p, q) \cdot S p (1)$ ，具有 $(n, n)$ 签名的 $S O (n, C)$ ，具有 $(2 n, 2 n)$ 签名的 $S O (n, H)$ ，具有（4, 3）签名的分裂型 $G_{2}$ ，具有（7, 7）签名的 $G_{2} (C)$ ，具有（4, 4）签名的 $S p i n (4, 3)$ ，具有（7, 7）签名的 $S p i n (7, C)$ ，具有（8, 8）签名的 $S p i n (5, 4)$ ，最后是具有（16, 16）签名的 $S p i n (9, C)$ 。分裂型和复化后的 $S p i n (9)$ 必然是局部对称的，如上述所述，因此不应出现在该列表中。复化后的全等群 $S O (n, C)$ ， $G_{2} (C)$ 和 $S p i n (7, C)$ 可以通过复化实数解析黎曼流形来实现。最后，具有包含在 $S O (n, H)$ 中的全等群的流形被 R. McLean 证明为局部平坦。[9]

　　黎曼对称空间，它们局部上是同胚于同类空间 $G / H$ 的流形，其局部全等群同构于 $H$ 。这些空间也已经被完全分类。

　　最后，伯杰的论文列出了具有无扭曲的仿射连接的流形可能的全等群；这一点将在下面讨论。

特殊全等群与旋量

　　具有特殊全等群的流形的特征是存在平行旋量场，即协变导数为零的旋量场。[10] 具体来说，以下事实成立：

当且仅当 $M$ 存在协变常数（或平行）投影纯旋量场时， $Hol (ω) \subset U (n)$ 。
如果 $M$ 是旋量流形，则当且仅当 $M$ 存在至少两个线性无关的平行纯旋量场时， $Hol (ω) \subset S U (n)$ 。实际上，一个平行的纯旋量场决定了结构群的规范化还原为 $S U (n)$ 。
如果 $M$ 是七维旋量流形，则当且仅当全等群包含在 $G_{2}$ 中时， $M$ 才携带非平凡的平行旋量场。
如果 $M$ 是八维旋量流形，则当且仅当全等群包含在 $S p i n (7)$ 中时， $M$ 才携带非平凡的平行旋量场。

　　单位全等群和特殊单位全等群通常与扭子理论[11]以及几乎复结构的研究[10]有关。

应用

　　 弦理论

　　具有特殊全等群的黎曼流形在弦理论紧化中起着重要作用。[12] 这是因为特殊全等群流形承认协变常数（平行）旋量场，从而保留了原始超对称性的一部分。最重要的是在 Calabi–Yau 流形上进行的 SU(2) 或 SU(3) 全等群的紧化。G2 流形上的紧化也很重要。

　　 机器学习

　　计算黎曼流形的全等群被提议作为在机器学习中学习数据流形结构的一种方式，尤其是在流形学习的背景下。由于全等群包含关于数据流形的全局结构的信息，它可以用来识别数据流形如何分解为子流形的乘积。由于有限采样效应，全等群无法精确计算，但可以使用谱图理论中的思想来构造一个数值近似，这与向量扩散映射类似。最终的算法——几何流形成分估计器（GeoManCEr）提供了对 de Rham 分解的数值近似，可以应用于实际数据。[13]

4. 仿射平行迁移群

　　仿射平行迁移群是那些来自无挠仿射联络（torsion-free affine connection）的平行迁移群；其中，不是黎曼或伪黎曼平行迁移群的，也被称为非度量平行迁移群。de Rham 分解定理不适用于仿射平行迁移群，因此对其进行完整分类是无法实现的。然而，对不可约仿射平行迁移群进行分类仍然是一个自然的目标。

　　在对黎曼平行迁移群进行分类的过程中，Berger 发展出了两个必须满足的标准，这两个标准适用于来自无挠仿射联络但不是局部对称的平行迁移群的李代数。其中一个标准，被称为Berger 的第一个标准，是 Ambrose-Singer 定理的推论，说明曲率张成平行迁移代数；另一个标准，被称为Berger 的第二个标准，来自联络不应是局部对称的要求。Berger 列出了一个作用不可约并满足这两个标准的群，这个列表可以理解为不可约仿射平行迁移群的可能列表。

　　后来发现，Berger 的列表并不完整：R. Bryant（1991 年）以及 Q. Chi、S. Merkulov 和 L. Schwachhöfer（1996 年）找到了更多的例子。这些有时被称为奇异平行迁移群（exotic holonomies）。这些新例子的探索最终促成了 Merkulov 和 Schwachhöfer 在 1999 年完成的不可约仿射平行迁移群的完整分类。Bryant（2000 年）进一步证明，他们列表中的每个群都确实可以作为某个仿射平行迁移群出现。

　　 Merkulov–Schwachhöfer 分类因其与某些对称空间（特别是厄米对称空间和四元数-凯勒对称空间）之间的联系而得到了极大澄清。这种关系在复仿射平行迁移群的情形下尤为清晰，正如 Schwachhöfer（2001 年）所展示的那样。

　　设 $V$ 是一个有限维复向量空间， $H \subset Aut (V)$ 是一个不可约半单复连通李子群， $K \subset H$ 是一个最大紧李子群。

如果存在一个不可约的厄米对称空间，其形式为 $G / (U (1) \cdot K)$ ，则 $H$ 和 $C^{*} \cdot H$ 都是非对称不可约仿射平行迁移群，其中 $V$ 是 $K$ 的切向量表示。
如果存在一个不可约的四元数-凯勒对称空间，其形式为 $G / (S p (1) \cdot K)$ ，则 $H$ 是一个非对称不可约仿射平行迁移群，当且仅当 $\dim V = 4$ 时， $C^{*} \cdot H$ 也是如此。在这里， $S p (1) \cdot K$ 的复化切向量表示是 $C^{2} \otimes V$ ，并且 $H$ 在 $V$ 上保持一个复辛几何形式。

　　除了以下情况，这两个系列包含了所有非对称不可约复仿射平行迁移群： $Sp (2, C) \cdot Sp (2 n, C) \subset Aut (C^{2} \otimes C^{2 n})$ $G_{2} (C) \subset Aut (C^{7})$ $Spin (7, C) \subset Aut (C^{8})$ 利用厄米对称空间的分类，第一个系列给出了以下复仿射平行迁移群： $Z_{C} \cdot SL (m, C) \cdot SL (n, C) \subset Aut (C^{m} \otimes C^{n})$ $Z_{C} \cdot SL (n, C) \subset Aut (Λ^{2} C^{n})$ $Z_{C} \cdot SL (n, C) \subset Aut (S^{2} C^{n})$ $Z_{C} \cdot SO (n, C) \subset Aut (C^{n})$ $Z_{C} \cdot Spin (10, C) \subset Aut (Δ_{10}^{+}) ≅ Aut (C^{16})$ $Z_{C} \cdot E_{6} (C) \subset Aut (C^{27})$ 其中 $Z_{C}$ 要么是平凡群，要么是群 $C^{*}$ 。

　　利用四元数-凯勒对称空间的分类，第二个系列给出了以下复辛几何平行迁移群： $Sp (2, C) \cdot SO (n, C) \subset Aut (C^{2} \otimes C^{n})$ $(Z_{C} \cdot) Sp (2 n, C) \subset Aut (C^{2 n})$ （在第二行，当 $n = 2$ 时， $Z_{C}$ 可以非平凡，否则 $Z_{C}$ 必须是平凡群。） $Z_{C} \cdot SL (2, C) \subset Aut (S^{3} C^{2})$ $Sp (6, C) \subset Aut (Λ_{0}^{3} C^{6}) ≅ Aut (C^{14})$ $SL (6, C) \subset Aut (Λ^{3} C^{6})$ $Spin (12, C) \subset Aut (Δ_{12}^{+}) ≅ Aut (C^{32})$ $E_{7} (C) \subset Aut (C^{56})$ 从这些列表中，可以观察到一个与 Simons 定理类似的结果，即黎曼几何平行迁移群在球面上作用是传递的：复几何平行迁移表示都是预同态向量空间。这个事实的概念性证明尚未被发现。

　　不可约实仿射平行迁移群的分类可以通过仔细分析得到，方法是使用上述列表和实仿射平行迁移群复合为复平行迁移群的事实。

5. 词源学

　　有一个类似的词，“holomorphic”（全纯的），由 Cauchy 的两位学生 Briot（1817–1882）和 Bouquet（1819–1895）引入，源自希腊语ὅλος（holos），意为 “整体的”，和μορφή（morphē），意为 “形式” 或 “外观”[14]。“holonomy” 这个词的词源与 “holomorphic” 的前半部分相同（holos）。关于后半部分：

　　 “在网上找到 holonomic（或 holonomy）这个词的词源非常困难。我发现了以下内容（感谢普林斯顿大学的 John Conway）：‘我相信它最早是由 Poinsot 在分析刚体运动时使用的。在这个理论中，如果在某种意义上可以从局部信息中恢复出全局信息，那么这个系统被称为‘holonomic’（全约束的），所以‘整体定律’的含义是非常合适的。比如，球体在桌面上滚动就是非 holonomic 的，因为沿着不同的路径滚动到同一个点时，球体可能会处于不同的朝向。然而，也许说‘holonomy’意味着‘整体定律’有点过于简化。‘nom’这个词根在希腊语中有许多交织的含义，或许更常指的是‘计数’。它来自与我们词汇‘number’（数字）相同的印欧语系词根。’” ——S. Golwala, [15] 见 νόμος（nomos）和 -nomy。

6. 参见

托马斯进动（Thomas precession）

7. 注释

Kobayashi & Nomizu 1963，第 II.7 节
Sharpe 1997，第 3.7 节
Spivak 1999，第 241 页
Sternberg 1964，第 VII.1.2 定理
Kobayashi & Nomizu 1963，第一卷，第 II.8 节
Kobayashi & Nomizu 1963，第 IV.5 节
该定理可推广到非单连通流形，但表述会更复杂。
Kobayashi & Nomizu 1963，第 IV.6 节
Bryant, Robert L. (1996), "Classical, exceptional, and exotic holonomies: a status report" (PDF), Actes de la Table Ronde de Géométrie Différentielle (Luminy, 1992), Sémin. Congr., vol. 1, Soc. Math. France, Paris, pp. 93–165, ISBN 2-85629-047-7, MR 1427757
Lawson & Michelsohn 1989，第 IV.9-10 节
Baum 等 1991
Gubser, S., Gubser S.; 等（编辑），《弦理论和 M 理论中的特殊平行迁移》+ Gubser, Steven S. (2004), 《弦、膜和额外维度》，TASI 2001。2001 年 TASI 暑期学校讲义，美国科罗拉多州博尔德，2001 年 6 月 4-29 日。River Edge, NJ: World Scientific, pp. 197–233, arXiv:hep-th/0201114, ISBN 978-981-238-788-2。
Pfau, David; Higgins, Irina; Botev, Aleksandar; Racanière, Sébastien (2020), 《Disentangling by Subspace Diffusion》, Advances in Neural Information Processing Systems, arXiv:2006.12982
Markushevich 2005
Golwala 2007, 第 65-66 页

8. 参考文献

Agricola, Ilka (2006), "The Srni lectures on non-integrable geometries with torsion", *Arch. Math.*, 42: 5–84, arXiv:math/0606705, Bibcode:2006math......6705A
Ambrose, Warren; Singer, Isadore (1953), "A theorem on holonomy", *Transactions of the American Mathematical Society*, 75 (3): 428–443, doi:10.2307/1990721, JSTOR 1990721
Baum, H.; Friedrich, Th.; Grunewald, R.; Kath, I. (1991), *Twistors and Killing spinors on Riemannian manifolds*, Teubner-Texte zur Mathematik, vol. 124, B.G. Teubner, ISBN 9783815420140
Berger, Marcel (1953), "Sur les groupes d'holonomie homogènes des variétés a connexion affines et des variétés riemanniennes", *Bull. Soc. Math. France*, 83: 279–330, MR 0079806, archived from the original on 2007-10-04
Besse, Arthur L. (1987), *Einstein manifolds*, Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], vol. 10, Springer-Verlag, ISBN 978-3-540-15279-8
Bonan, Edmond (1965), "Structure presque quaternale sur une variété différentiable", *C. R. Acad. Sci. Paris*, 261: 5445–8.
Bonan, Edmond (1966), "Sur les variétés riemanniennes à groupe d'holonomie G2 ou Spin(7)", *C. R. Acad. Sci. Paris*, 320: 127–9.
Borel, Armand; Lichnerowicz, André (1952), "Groupes d'holonomie des variétés riemanniennes", *Les Comptes rendus de l'Académie des sciences*, 234: 1835–7, MR 0048133
Bryant, Robert L. (1987), "Metrics with exceptional holonomy", *Annals of Mathematics*, 126 (3): 525–576, doi:10.2307/1971360, JSTOR 1971360.
Bryant, Robert L. (1991), "Two exotic holonomies in dimension four, path geometries, and twistor theory", *Complex Geometry and Lie Theory*, Proceedings of Symposia in Pure Mathematics, vol. 53, pp. 33–88, doi:10.1090/pspum/053/1141197, ISBN 9780821814925
Bryant, Robert L. (2000), "Recent Advances in the Theory of Holonomy", *Astérisque*, Séminaire Bourbaki 1998–1999, 266: 351–374, arXiv:math/9910059
Cartan, Élie (1926), "Sur une classe remarquable d'espaces de Riemann", *Bulletin de la Société Mathématique de France*, 54: 214–264, doi:10.24033/bsmf.1105, ISSN 0037-9484, MR 1504900
Cartan, Élie (1927), "Sur une classe remarquable d'espaces de Riemann", *Bulletin de la Société Mathématique de France*, 55: 114–134, doi:10.24033/bsmf.1113, ISSN 0037-9484
Chi, Quo-Shin; Merkulov, Sergey A.; Schwachhöfer, Lorenz J. (1996), "On the Incompleteness of Berger's List of Holonomy Representations", *Invent. Math.*, 126 (2): 391–411, arXiv:dg-da/9508014, Bibcode:1996InMat.126..391C, doi:10.1007/s002220050104, S2CID 119124942
Golwala, S. (2007), *Lecture Notes on Classical Mechanics for Physics 106ab* (PDF)
Joyce, D. (2000), *Compact Manifolds with Special Holonomy*, Oxford University Press, ISBN 978-0-19-850601-0
Kobayashi, S.; Nomizu, K. (1963), *Foundations of Differential Geometry*, Vol. 1 & 2 (New ed.), Wiley-Interscience (published 1996), ISBN 978-0-471-15733-5
Kraines, Vivian Yoh (1965), "Topology of quaternionic manifolds", *Bull. Amer. Math. Soc.*, 71, 3, 1 (3): 526–7, doi:10.1090/s0002-9904-1965-11316-7.
Lawson, H. B.; Michelsohn, M-L. (1989), *Spin Geometry*, Princeton University Press, ISBN 978-0-691-08542-5
Lichnerowicz, André (2011) [1976], *Global Theory of Connections and Holonomy Groups*, Springer, ISBN 9789401015523
Markushevich, A.I. (2005) [1977], Silverman, Richard A. (ed.), *Theory of functions of a Complex Variable* (2nd ed.), American Mathematical Society, p. 112, ISBN 978-0-8218-3780-1
Merkulov, Sergei A.; Schwachhöfer, Lorenz J. (1999), "Classification of irreducible holonomies of torsion-free affine connections", *Annals of Mathematics*, 150 (1): 77–149, arXiv:math/9907206, doi:10.2307/121098, JSTOR 121098, S2CID 17314244; Merkulov, Sergei; Schwachhöfer, Lorenz (1999), "Addendum", *Ann. of Math.*, 150 (3): 1177–9, arXiv:math/9911266, doi:10.2307/121067, JSTOR 121067, S2CID 197437925.
Olmos, C. (2005), "A geometric proof of the Berger Holonomy Theorem", *Annals of Mathematics*, 161 (1): 579–588, doi:10.4007/annals.2005.161.579
Sharpe, Richard W. (1997), *Differential Geometry: Cartan's Generalization of Klein's Erlangen Program*, Springer-Verlag, ISBN 978-0-387-94732-7, MR 1453120
Schwachhöfer, Lorenz J. (2001), "Connections with irreducible holonomy representations", *Advances in Mathematics*, 160 (1): 1–80, doi:10.1006/aima.2000.1973
Simons, James (1962), "On the transitivity of holonomy systems", *Annals of Mathematics*, 76 (2): 213–234, doi:10.2307/1970273, JSTOR 1970273, MR 0148010
Spivak, Michael (1999), *A comprehensive introduction to differential geometry*, vol. II, Houston, Texas: Publish or Perish, ISBN 978-0-914098-71-3
Sternberg, S. (1964), *Lectures on differential geometry*, Chelsea, ISBN 978-0-8284-0316-0

9. 进一步阅读

关于特殊 holonomy 流形的文献，Frederik Witt 编制的参考书目。

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。