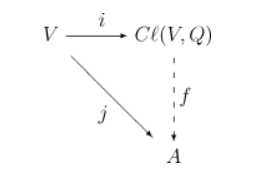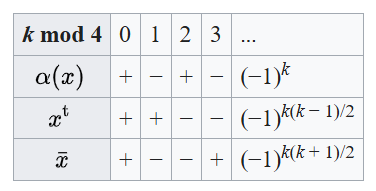克利福德代数（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在数学中，克利福德代数 \(^\text{[a]}\) 是由具备二次型的向量空间生成的一类代数。它是一个带有单位元的结合代数，同时具有一个特定子空间这一附加结构。作为 $K$-代数，它们推广了实数、复数、四元数以及若干其他超复数体系。\(^\text{[1][2]}\) 克利福德代数理论与二次型理论及正交变换理论紧密相关。克利福德代数在几何学、理论物理以及数字图像处理等诸多领域中具有重要应用。该名称源自英国数学家威廉·金登·克利福德（William Kingdon Clifford, 1845–1879）。

　　 在所有克利福德代数中，最为常见的是正交克利福德代数，它们亦称为（伪）黎曼克利福德代数，以区别于辛克利福德代数。\(^\text{[b]}\)

1. 引言与基本性质

　　 克利福德代数是一个包含并由向量空间 $V$ 生成的有单位元的结合代数，其中 $V$ 定义在一个域 $K$ 上，并配备有一个二次型 $Q: V \to K$。克利福德代数 $\mathrm{Cl}(V, Q)$ 是满足如下条件的 “最自由”[c] 有单位元结合代数： $$ v^{2} = Q(v) \cdot 1 \quad \text{对所有 } v \in V,~ $$ 其中左侧的乘积是代数内部的乘法，而右侧的 $1$ 表示代数的乘法单位元（需注意，不同于域 $K$ 的乘法单位元）。这里 “最自由” 或 “最一般” 的含义，可以通过泛性质的概念形式化地加以刻画，如下所述。

　　 当 $V$ 是有限维实向量空间且 $Q$ 非退化时，$\mathrm{Cl}(V, Q)$ 可以记作 $\mathrm{Cl}_{p,q}(\mathbf{R})$。这表示 $V$ 存在一个正交基，其中 $p$ 个基向量满足 $e_i^2 = +1$，而 $q$ 个基向量满足 $e_i^2 = -1$；$\mathbf{R}$ 表明这是定义在实数上的克利福德代数，即代数元素的系数均为实数。该基底可通过正交对角化方法获得。

　　 由向量空间 $V$ 生成的自由代数可写作张量代数 $\bigoplus_{n \geq 0} V^{\otimes n}$,即所有 $n$ 重张量积的直和。于是，克利福德代数可表述为该张量代数关于双边理想的商，其中理想由以下形式的元素生成：$v \otimes v - Q(v) \cdot 1, \quad \forall v \in V$.在商代数中，由张量积诱导的乘法通常用并置表示（例如 $uv$）。其结合性直接源于张量积的结合性。

　　 克利福德代数具有一个特定子空间 $V$，即嵌入映射的像。然而，一般来说，给定一个与克利福德代数同构的 $K$-代数，并不能唯一确定这样的子空间。

　　 若底域 $K$ 中的 2 可逆，则上述基本恒等式可以改写为 $$ uv + vu = 2 \langle u, v \rangle \cdot 1 \quad \forall u, v \in V,~ $$ 其中 $$ \langle u, v \rangle = \tfrac{1}{2}\big(Q(u+v) - Q(u) - Q(v)\big)~ $$ 是通过极化恒等式由二次型 $Q$ 所关联的对称双线性型。

　　 在此方面，特征为 2 的情形构成一个特殊情况。特别地，当 $\mathrm{char}(K) = 2$ 时，二次型并不一定能够唯一地决定一个满足 $Q(v) = \langle v, v \rangle$ 的对称双线性型。\(^\text{[3]}\) 因此，本文中的许多叙述均附带条件：底域的特征不为 2；若去除此条件，结论即不再成立。

作为外代数的量子化

　　 克利福德代数与外代数密切相关。事实上，当 $Q = 0$ 时，克利福德代数 $\mathrm{Cl}(V, Q)$ 正是外代数 $\bigwedge V$。当底域 $K$ 中的 $2$ 可逆时，存在一个典范线性同构，将 $\bigwedge V$ 与 $\mathrm{Cl}(V, Q)$ 联系起来。也就是说，它们作为向量空间是天然同构的，但其乘法结构不同（在特征为 2 的情况下，它们依然是向量空间同构的，只是该同构不再是天然的）。克利福德代数中的乘法结合其特定子空间，比外代数的外积更加丰富，因为它利用了二次型 $Q$ 所提供的额外信息。

　　 克利福德代数是一个滤过代数；其相关的分次代数正是外代数。

　　 更准确地说，克利福德代数可以被看作是外代数的一种量子化（参见量子群），正如魏尔代数是对称代数的量子化一样。

　　 魏尔代数与克利福德代数还具备进一步的 *-代数结构，它们可以统一地理解为超代数的偶次项与奇次项，这一点在 CCR 与 CAR 代数的研究中已有论述。

2. 泛性质与构造

　　 设 $V$ 是定义在域 $K$ 上的一个向量空间，且 $Q : V \to K$ 是 $V$ 上的一个二次型。在大多数感兴趣的情形中，域 $K$ 是实数域 $\mathbf{R}$、复数域 $\mathbf{C}$，或某个有限域。

　　 一个克利福德代数 $\mathrm{Cl}(V, Q)$ 是一对 $(B, i)$[d][4]，其中 $B$ 是一个定义在 $K$ 上的有单位元结合代数，$i : V \to B$ 是一个线性映射，并满足 $i(v)^2 = Q(v) \cdot 1_B, \quad \forall v \in V$,这里 $1_B$ 表示代数 $B$ 的乘法单位元。其定义依赖于以下泛性质：若给定任意一个定义在 $K$ 上的有单位元结合代数 $A$，以及任意线性映射 $j : V \to A$，满足 $$ j(v)^2 = Q(v) \cdot 1_A, \quad \forall v \in V,~ $$ 其中 $1_A$ 表示代数 $A$ 的乘法单位元，则存在唯一的代数同态 $f : B \to A$ 使得下列图表交换（即 $f \circ i = j$）。

图
图 1

　　 二次型 $Q$ 可以被（不必对称的[5]）双线性型 $\langle \cdot, \cdot \rangle$ 取代，只要它满足 $\langle v, v \rangle = Q(v), \quad \forall v \in V$.此时对 $j$ 的等价要求为 $$ j(v) j(v) = \langle v, v \rangle \cdot 1_A, \quad \forall v \in V.~ $$ 当域的特征不为 2 时，该条件又可等价改写为： $$ j(v) j(w) + j(w) j(v) = \big(\langle v, w \rangle + \langle w, v \rangle\big)\cdot 1_A, \quad \forall v, w \in V,~ $$ 其中，双线性型在不失一般性的情况下还可以进一步要求为对称双线性型。

　　 如上所述，克利福德代数总是存在的，其构造方法如下：从包含 $V$ 的最一般代数开始，即张量代数 $T(V)$，然后通过取适当的商来强制满足基本恒等式。在此，我们取 $T(V)$ 中由以下元素生成的双边理想 $I_Q$： $$ v \otimes v - Q(v) \cdot 1, \quad \forall v \in V,~ $$ 并定义克利福德代数为该商代数： $$ \operatorname{Cl}(V, Q) = T(V) / I_Q.~ $$ 该商代数所继承的环乘法有时被称为克利福德乘法[6]，以区别于外积和数量积。

　　 随后可直接验证，$\operatorname{Cl}(V, Q)$ 包含 $V$，并满足上述的泛性质，因此 $\operatorname{Cl}(V, Q)$ 在唯一同构意义下是唯一的；这也是通常称为 “克利福德代数 $\operatorname{Cl}(V, Q)$” 的原因。此外，该构造还蕴含了嵌入映射 $i$ 是单射。通常在表述时会省略 $i$，直接将 $V$ 视为 $\operatorname{Cl}(V, Q)$ 的一个线性子空间。

　　 克利福德代数的泛性质刻画表明，$\operatorname{Cl}(V, Q)$ 的构造本质上是函子性的。换言之，$\operatorname{Cl}$ 可以被视为一个函子：从 “带二次型的向量空间” 范畴（其态射为保持二次型的线性映射）到 “结合代数” 范畴。泛性质保证了：在保持二次型的前提下，向量空间之间的线性映射可以唯一扩张为相应克利福德代数之间的代数同态。

3. 基与维数

　　 由于向量空间 $V$ 配备了一个二次型 $Q$，在特征不等于 $2$ 的情况下，$V$ 总是存在正交基。正交基的定义是：对于某个对称双线性型，满足 $$ \langle e_i, e_j \rangle = 0, \quad i \neq j,~ $$ 以及 $$ \langle e_i, e_i \rangle = Q(e_i).~ $$ 克利福德基本恒等式蕴含了对于正交基有： $$ e_i e_j = - e_j e_i, \quad i \neq j,~ $$ 并且 $$ e_i^2 = Q(e_i).~ $$ 这使得对正交基向量的操作大为简化。若取一组互不相同的正交基向量的乘积 $e_{i_1} e_{i_2} \cdots e_{i_k}$,则总可以通过有限次两两交换将其排成标准顺序，而总体符号由所需交换次数的奇偶性（即置换的符号）决定。

　　 设 $V$ 在域 $K$ 上的维数为 $n$，并且 $\{e_1, \ldots, e_n\}$ 是 $(V, Q)$ 的一个正交基，则克利福德代数 $\operatorname{Cl}(V, Q)$ 在 $K$ 上是自由的，其一组基可以写作： $$ \big\{\, e_{i_1} e_{i_2} \cdots e_{i_k} \;\big|\; 1 \leq i_1 < i_2 < \cdots < i_k \leq n, \; 0 \leq k \leq n \,\big\}.~ $$ 其中，当 $k = 0$ 时的 “空乘积” 被定义为代数的乘法单位元。对每一个固定的 $k$，基元素的数量为 $\binom{n}{k}$，因此克利福德代数的总维数为： $$ \dim \operatorname{Cl}(V, Q) = \sum_{k=0}^n \binom{n}{k} = 2^n.~ $$

4. 例子：实克利福德代数与复克利福德代数

　　 最重要的克利福德代数是那些定义在实向量空间与复向量空间上的，并且配备有非退化二次型的情形。

　　 每一个代数 $\mathrm{Cl}_{p,q}(\mathbf{R})$ 与 $\mathrm{Cl}_{n}(\mathbf{C})$ 都同构于 $A$ 或 $A \oplus A$，其中 $A$ 是一个满矩阵环，其元素取自 $\mathbf{R}$、$\mathbf{C}$ 或 $\mathbf{H}$（四元数）。关于这些代数的完整分类，可参见 克利福德代数的分类。

实数情形

　　 克利福德代数有时也被称为几何代数，尤其是在实数域上的情形。

　　 任意有限维实向量空间上的非退化二次型，都与如下标准对角形式等价： $$ Q(v) = v_1^2 + \cdots + v_p^2 - v_{p+1}^2 - \cdots - v_{p+q}^2,~ $$ 其中 $n = p + q$ 是向量空间的维数。整数对 $(p, q)$ 被称为该二次型的符号型。带有此二次型的实向量空间通常记作 $\mathbb{R}^{p,q}$。其上的克利福德代数记作 $\mathrm{Cl}_{p,q}(\mathbf{R})$。符号 $\mathrm{Cl}_n(\mathbf{R})$ 则指 $\mathrm{Cl}_{n,0}(\mathbf{R})$ 或 $\mathrm{Cl}_{0,n}(\mathbf{R})$，这取决于作者倾向于使用正定空间还是负定空间。

　　 $\mathbf{R}^{p,q}$ 的一个标准基 $\{e_1, \ldots, e_n\}$ 由 $n = p+q$ 个两两正交向量组成，其中有 $p$ 个基向量平方等于 $+1$，另有 $q$ 个基向量平方等于 $-1$。因此，在 $\mathrm{Cl}_{p,q}(\mathbf{R})$ 中，就有 $p$ 个平方为 $+1$ 的向量与 $q$ 个平方为 $-1$ 的向量。

　　 若干低维情形

复数情形

　　 同样可以研究复向量空间上的克利福德代数。任意一个维数为 $n$ 的复向量空间上的非退化二次型，都与如下标准对角形式等价： $$ Q(z) = z_1^2 + z_2^2 + \cdots + z_n^2.~ $$ 因此，对于每一个维数 $n$，在同构意义下，带有非退化二次型的复向量空间仅对应唯一一个克利福德代数。我们将配备标准二次型的 $\mathbf{C}^n$ 上的克利福德代数记作 $\mathrm{Cl}_n(\mathbf{C})$。

　　 对于若干低维情形，可以得到：

　　 其中 $M_n(\mathbf{C})$ 表示所有 $n \times n$ 复矩阵所构成的代数。

5. 例子：构造四元数与对偶四元数

四元数

　　 在本节中，哈密顿的四元数将被构造为克利福德代数 $\mathrm{Cl}_{3,0}(\mathbf{R})$ 的偶子代数。

　　 设向量空间 $V$ 为实三维空间 $\mathbf{R}^3$，其二次型为通常的欧几里得二次型。于是，对于 $v, w \in \mathbf{R}^3$，我们有双线性型（即数量积）： $$ v \cdot w = v_1 w_1 + v_2 w_2 + v_3 w_3.~ $$ 现在引入向量 $v, w$ 的克利福德乘积： $$ vw + wv = 2 (v \cdot w).~ $$ 记 $\mathbf{R}^3$ 的一组正交单位向量为 $\{e_1, e_2, e_3\}$，则克利福德乘法给出以下关系： $$ e_2 e_3 = - e_3 e_2, \quad e_1 e_3 = - e_3 e_1, \quad e_1 e_2 = - e_2 e_1,~ $$ 以及 $$ e_1^2 = e_2^2 = e_3^2 = 1.~ $$ 因此，克利福德代数 $\mathrm{Cl}_{3,0}(\mathbf{R})$ 的一个一般元素可写为： $$ A = a_0 + a_1 e_1 + a_2 e_2 + a_3 e_3 + a_4 e_2 e_3 + a_5 e_1 e_3 + a_6 e_1 e_2 + a_7 e_1 e_2 e_3,~ $$ 其中 $a_0, a_1, \ldots, a_7 \in \mathbf{R}$。

　　 偶次数元素的线性组合构成了 $\mathrm{Cl}_{3,0}(\mathbf{R})$ 的偶子代数 $\mathrm{Cl}^{[0]}_{3,0}(\mathbf{R})$，其一般元素为： $$ q = q_0 + q_1 e_2 e_3 + q_2 e_1 e_3 + q_3 e_1 e_2,~ $$ 其中 $q_0, q_1, q_2, q_3 \in \mathbf{R}$。

　　 基元素可与四元数的标准基 $i, j, k$ 对应如下： $$ i = e_2 e_3, \quad j = e_1 e_3, \quad k = e_1 e_2,~ $$ 这表明偶子代数 $\mathrm{Cl}^{[0]}_{3,0}(\mathbf{R})$ 正是哈密顿的实四元数代数。

　　 为了验证这一点，计算如下： $$ i^2 = (e_2 e_3)^2 = e_2 e_3 e_2 e_3 = - e_2 e_2 e_3 e_3 = -1,~ $$ 以及 $$ ij = e_2 e_3 e_1 e_3 = - e_2 e_3 e_3 e_1 = - e_2 e_1 = e_1 e_2 = k.~ $$ 最后： $$ ijk = e_2 e_3 e_1 e_3 e_1 e_2 = -1.~ $$

对偶四元数

　　 在本节中，对偶四元数将被构造为实四维空间上某个带有退化二次型的克利福德代数的偶子代数。\(^\text{[9][10]}\)

　　 设向量空间 $V$ 为实四维空间 $\mathbf{R}^4$，其二次型 $Q$ 为由 $\mathbf{R}^3$ 上欧几里得度量导出的一个退化型。对 $v, w \in \mathbf{R}^4$，定义退化双线性型： $$ d(v, w) = v_1 w_1 + v_2 w_2 + v_3 w_3.~ $$ 该退化的数量积实质上是将 $\mathbf{R}^4$ 中的距离测度投影到 $\mathbf{R}^3$ 的超平面上。

　　 向量 $v, w$ 的克利福德乘积定义为： $$ vw + wv = - 2\, d(v, w).~ $$ 注意，这里的负号是特意引入的，以便简化与四元数的对应关系。

　　 记 $\mathbf{R}^4$ 的一组两两正交单位向量为 $\{e_1, e_2, e_3, e_4\}$，则克利福德乘法给出以下关系： $$ e_m e_n = - e_n e_m, \quad m \neq n,~ $$ 以及 $$ e_1^2 = e_2^2 = e_3^2 = -1, \quad e_4^2 = 0.~ $$ $\operatorname{Cl}(\mathbf{R}^4, d)$ 的一般元素共有 16 个分量。其偶次数元素的线性组合定义了偶子代数 $\operatorname{Cl}^{[0]}(\mathbf{R}^4, d)$，其一般元素为： $$ H = h_0 + h_1 e_2 e_3 + h_2 e_3 e_1 + h_3 e_1 e_2 + h_4 e_4 e_1 + h_5 e_4 e_2 + h_6 e_4 e_3 + h_7 e_1 e_2 e_3 e_4,~ $$ 其中 $h_0, \ldots, h_7 \in \mathbf{R}$。

　　 这些基元素可以与四元数的基 $i, j, k$ 以及对偶单位 $\varepsilon$ 对应如下： $$ i = e_2 e_3, \quad j = e_3 e_1, \quad k = e_1 e_2, \quad \varepsilon = e_1 e_2 e_3 e_4.~ $$ 这建立了 $\operatorname{Cl}^{[0]}_{0,3,1}(\mathbf{R})$ 与对偶四元数代数之间的对应关系。

　　 为了验证这一点，计算如下： $$ \varepsilon^2 = (e_1 e_2 e_3 e_4)^2 = e_1 e_2 e_3 e_4 e_1 e_2 e_3 e_4 = - e_1 e_2 e_3 (e_4 e_4) e_1 e_2 e_3 = 0,~ $$ 以及 $$ \varepsilon i = (e_1 e_2 e_3 e_4) e_2 e_3 = e_1 e_2 e_3 e_4 e_2 e_3 = e_2 e_3 (e_1 e_2 e_3 e_4) = i \varepsilon.~ $$ 交换 $e_1$ 与 $e_4$ 时符号会交替出现，但总次数为偶数，因此对偶单位 $\varepsilon$ 与四元数基 $i, j, k$ 可交换。

6. 例子：低维情形

　　 设 $K$ 是一个特征不为 2 的任意域。

维数 1

　　 当 $\dim V = 1$ 时，若二次型 $Q$ 可对角化为 $\operatorname{diag}(a)$，即存在非零向量 $x$ 使得 $Q(x) = a$，则 $\operatorname{Cl}(V, Q)$ 代数同构于一个由元素 $x$ 所生成的 $K$-代数，其中 $x^2 = a$,即二次代数 $K[X] / (X^2 - a)$.特别地，若 $a = 0$（即 $Q$ 是零二次型），则 $\operatorname{Cl}(V, Q)$ 代数同构于 对偶数代数 $K[\varepsilon]/(\varepsilon^2)$。

　　 若 $a$ 是 $K$ 中的非零平方数，则 $\operatorname{Cl}(V, Q) \simeq K \oplus K$.

　　 否则，$\operatorname{Cl}(V, Q)$ 同构于 $K$ 的二次域扩张 $K(\sqrt{a})$。

维数 2

　　 当 $\dim V = 2$ 时，若二次型 $Q$ 可对角化为 $\operatorname{diag}(a, b)$，其中 $a, b \neq 0$（若 $Q$ 非退化，则这种对角化总是存在），则 $\operatorname{Cl}(V, Q)$ 同构于一个由元素 $x, y$ 生成的 $K$-代数，满足：$x^2 = a, \quad y^2 = b, \quad xy = - yx$.

　　 因此：$\operatorname{Cl}(V, Q) \simeq (a, b)_K$,即（广义）四元数代数。当 $a = b = -1$ 且 $K = \mathbb{R}$ 时，我们正好得到哈密顿的四元数代数：$\mathbb{H} = (-1, -1)_{\mathbb{R}}$.

　　 作为一个特例，若存在某个 $x \in V$ 满足 $Q(x) = 1$，则有 $\operatorname{Cl}(V, Q) \simeq M_2(K)$,其中 $M_2(K)$ 表示所有 $2 \times 2$ 的 $K$-矩阵代数。

7. 性质

与外代数的关系

　　 给定一个向量空间 $V$，我们可以构造其外代数 $\bigwedge V$，其定义不依赖于 $V$ 上的任何二次型。事实表明：若域 $K$ 的特征不等于 2，则作为向量空间，$\bigwedge V$ 与 $\operatorname{Cl}(V, Q)$ 之间存在一个天然同构（在特征为 2 的情况下，同构仍然存在，但不一定是天然的）。该同构在代数层面上成立的充要条件是 $Q = 0$。因此，可以将克利福德代数 $\operatorname{Cl}(V, Q)$ 视为外代数 $\bigwedge V$ 的一种丰富化（更准确地说，是一种量子化；参见前文的引言），其乘法依赖于二次型 $Q$（尽管外积仍可在不依赖于 $Q$ 的情况下独立定义）。

　　 建立这一同构的最简单方式是：在 $V$ 中选取一个正交基 $\{e_1, \ldots, e_n\}$，并将其扩展为 $\operatorname{Cl}(V, Q)$ 的基（如前所述）。则映射 $\operatorname{Cl}(V, Q) \;\longrightarrow\; \bigwedge V$ 由下式决定：$e_{i_1} e_{i_2} \cdots e_{i_k} \;\mapsto\; e_{i_1} \wedge e_{i_2} \wedge \cdots \wedge e_{i_k}$.

　　 需要注意的是，这一构造仅在基 $\{e_1, \ldots, e_n\}$ 为正交基时有效。但可以证明，该映射与正交基的具体选择无关，因此它给出了一个天然的同构。

　　 若域 $K$ 的特征为 $0$，则还可以通过反对称化来建立该同构。定义函数 $f_k : V \times \cdots \times V \;\longrightarrow\; \operatorname{Cl}(V, Q)$ 为 $$ f_k(v_1, \ldots, v_k) = \frac{1}{k!} \sum_{\sigma \in S_k} \operatorname{sgn}(\sigma)\, v_{\sigma(1)} \cdots v_{\sigma(k)},~ $$ 其中求和遍历对称群 $S_k$。由于 $f_k$ 是交替的，它诱导出一个唯一的线性映射 $\bigwedge\nolimits^k V \;\longrightarrow\; \operatorname{Cl}(V, Q)$.这些映射的直和给出了一个 $\bigwedge V$ 与 $\operatorname{Cl}(V, Q)$ 之间的线性映射。可以证明，该映射是一个线性同构，并且是天然的。

　　 更高层次的理解方式是：在 $\operatorname{Cl}(V, Q)$ 上构造一个滤过。回忆张量代数 $T(V)$ 具有一个自然的滤过：$F_0 \subset F_1 \subset F_2 \subset \cdots$,其中 $F^k$ 包含所有阶数 $\leq k$ 的张量的和。将其投射到克利福德代数上，可以得到 $\operatorname{Cl}(V, Q)$ 的一个滤过。于是相关的分次代数为 $$ \operatorname{Gr}_F \operatorname{Cl}(V, Q) = \bigoplus_k F^k / F^{k-1},~ $$ 它天然同构于外代数 $\bigwedge V$。由于一个滤过代数的相关分次代数总是与该滤过代数在滤过向量空间意义下同构（方法是对每个 $k$ 选择 $F^k$ 在 $F^{k+1}$ 中的补空间），因此这一方法在任意特征下（包括特征为 2 的情形）都给出了一个同构，尽管该同构不一定是天然的。

分次结构

　　 在以下内容中，假设域 $K$ 的特征不等于 2。\(^\text{[e]}\)

　　 克利福德代数是一个 $\mathbf{Z}_2$-分次代数（亦称超代数，superalgebra）。事实上，定义在 $V$ 上的线性映射 $v \;\mapsto\; -v$（即关于原点的反射）保持二次型 $Q$ 不变，因此依据克利福德代数的泛性质，它可以唯一扩张为一个代数自同构： $$ \alpha : \operatorname{Cl}(V, Q) \;\longrightarrow\; \operatorname{Cl}(V, Q).~ $$ 由于 $\alpha$ 是一个对合（involution，即其平方为恒等映射），于是 $\operatorname{Cl}(V, Q)$ 可以分解为 $\alpha$ 的正、负特征子空间： $$ \operatorname{Cl}(V, Q) = \operatorname{Cl}^{[0]}(V, Q) \;\oplus\; \operatorname{Cl}^{[1]}(V, Q),~ $$ 其中 $$ \operatorname{Cl}^{[i]}(V, Q) = \{\, x \in \operatorname{Cl}(V, Q) \;\mid\; \alpha(x) = (-1)^i x \,\}.~ $$ 由于 $\alpha$ 是代数自同构，因此有： $$ \operatorname{Cl}^{[i]}(V, Q)\; \operatorname{Cl}^{[j]}(V, Q) \;=\; \operatorname{Cl}^{[i+j]}(V, Q),~ $$ 其中上标取模 2。由此，$\operatorname{Cl}(V, Q)$ 获得了一个 $\mathbf{Z}_2$-分次代数的结构。子空间 $\operatorname{Cl}^{[0]}(V, Q)$ 构成 $\operatorname{Cl}(V, Q)$ 的一个子代数，称为偶子代数；子空间 $\operatorname{Cl}^{[1]}(V, Q)$ 称为 $\operatorname{Cl}(V, Q)$ 的奇部分，但它并不是一个子代数。这种 $\mathbf{Z}_2$-分次结构在克利福德代数的分析与应用中具有重要作用。自同构 $\alpha$ 被称为主对合或次数对合。在这一 $\mathbf{Z}_2$-分次下的纯元素，分别称为偶元素或奇元素。

　　 克利福德代数并不是一个 $\mathbf{Z}$-分次代数，而是一个 $\mathbf{Z}$-滤过代数（$\mathbb{Z}$-filtered algebra）。其中 $\operatorname{Cl}^{\leqslant i}(V, Q)$ 表示由至多 $i$ 个 $V$ 中元素的乘积所张成的子空间，并且满足： $$ \operatorname{Cl}^{\leqslant i}(V, Q) \cdot \operatorname{Cl}^{\leqslant j}(V, Q) \;\subset\; \operatorname{Cl}^{\leqslant i+j}(V, Q).~ $$ 通常所说的 “克利福德数的次数” 是指其在 $\mathbb{Z}$-分次中的次数。

　　 一个克利福德代数的偶子代数 $\operatorname{Cl}^{[0]}(V, Q)$ 本身同构于另一个克利福德代数。[f][g]具体而言，若 $V$ 可以分解为一个非零范数向量 $a$（满足 $Q(a) \neq 0$）与子空间 $U$ 的正交直和，则有： $$ \operatorname{Cl}^{[0]}(V, Q) \;\cong\; \operatorname{Cl}\bigl(U,\, -Q(a)\, Q|_U \bigr),~ $$ 其中 $Q|_U$ 表示二次型 $Q$ 在子空间 $U$ 上的限制。

　　 特别地，在实数域的情形下，这意味着： $$ \operatorname{Cl}^{[0]}_{p,q}(\mathbf{R}) \;\cong\; \begin{cases} \operatorname{Cl}_{p,\,q-1}(\mathbf{R}), & q > 0, \\[6pt] \operatorname{Cl}_{q,\,p-1}(\mathbf{R}), & p > 0, \end{cases}~ $$ 在负定情形下，这给出了一个包含关系：$\operatorname{Cl}_{0,\,n-1}(\mathbf{R}) \;\subset\; \operatorname{Cl}_{0,\,n}(\mathbf{R})$, 它扩展了如下序列： $$ \mathbf{R} \;\subset\; \mathbf{C} \;\subset\; \mathbf{H} \;\subset\; \mathbf{H} \oplus \mathbf{H} \;\subset\; \cdots~ $$ 同样地，在复数情形下，可以证明：$\operatorname{Cl}_n(\mathbf{C}) \;\cong\; \operatorname{Cl}_{n-1}(\mathbf{C})$.

反自同构

　　 除了自同构 $\alpha$ 之外，还有两个反自同构在克利福德代数的分析中起着重要作用。回忆张量代数 $T(V)$ 上存在一个自然的反自同构，它将所有向量积的顺序反转： $$ v_1 \otimes v_2 \otimes \cdots \otimes v_k \;\longmapsto\; v_k \otimes \cdots \otimes v_2 \otimes v_1.~ $$ 由于理想 $I_Q$ 在这一操作下保持不变，该操作可传递至克利福德代数 $\operatorname{Cl}(V, Q)$，称为转置或反序运算，记作 $x^{\mathrm{t}}$。转置是一个反自同构，满足：$(xy)^{\mathrm{t}} = y^{\mathrm{t}} x^{\mathrm{t}}$.转置运算不涉及 $\mathbf{Z}_2$-分次，因此我们可以通过将 $\alpha$ 与转置运算复合来定义第二个反自同构。该运算称为克利福德共轭，记作 $\bar{x}$： $$ \bar{x} = \alpha(x^{\mathrm{t}}) = \alpha(x)^{\mathrm{t}}.~ $$ 在这两个反自同构中，转置被认为是更为基本的。\(^\text{[h]}\)

　　 需要注意的是，这些运算全都是对合。可以证明，它们在 $\mathbf{Z}_2$-分次下的纯元素上作用结果为 $\pm 1$。事实上，这三类运算只依赖于元素次数模 4 的余数。也就是说，若 $x$ 是次数为 $k$ 的纯元素，则有： $$ \alpha(x) = \pm x, \quad x^{\mathrm{t}} = \pm x, \quad \bar{x} = \pm x.~ $$ 其中符号由下表给出：

图
图 2

克利福德数量积

　　 当底域特征不为 2 时，向量空间 $V$ 上的二次型 $Q$ 可以扩张为整个克利福德代数 $\operatorname{Cl}(V, Q)$ 上的一个二次型（亦记作 $Q$）。其一个与基无关的定义为： $$ Q(x) = \langle x^{\mathrm{t}} x \rangle_0,~ $$ 其中 $\langle a \rangle_0$ 表示 $a$ 的标量部分（即在 $\mathbf{Z}$-分次中的次数为 0 的部分）。可以证明，对于 $v_i \in V$： $$ Q(v_1 v_2 \cdots v_k) = Q(v_1) Q(v_2) \cdots Q(v_k),~ $$ 但这一恒等式并不对 $\operatorname{Cl}(V, Q)$ 的任意元素成立。相应的对称双线性型定义为： $$ \langle x, y \rangle = \langle x^{\mathrm{t}} y \rangle_0.~ $$ 容易验证，当其限制在 $V$ 上时，便退化为原始的双线性型。并且，该双线性型在 $\operatorname{Cl}(V, Q)$ 上非退化，当且仅当它在 $V$ 上非退化。

　　 此外，左（或右）克利福德乘法与转置之间满足伴随关系。具体地，元素 $a \in \operatorname{Cl}(V, Q)$ 的转置 $a^{\mathrm{t}}$ 定义了左（或右）乘算子的伴随： $$ \langle a x, y \rangle = \langle x, a^{\mathrm{t}} y \rangle,~ $$ 以及 $$ \langle x a, y \rangle = \langle x, y a^{\mathrm{t}} \rangle.~ $$

8. 克利福德代数的结构

　　 在本节中，我们假设底域的特征不为 2，向量空间 $V$ 是有限维的，并且二次型 $Q$ 所对应的对称双线性型是非退化的。

　　 一个中心单代数是指：在域 $K$ 上的矩阵代数，其矩阵元取自某个以 $K$ 为中心的有限维除代数。例如，在实数域上的中心单代数是实数矩阵代数或四元数矩阵代数。在此条件下，克利福德代数的结构可以归纳如下：

　　 克利福德代数的结构可以通过以下结果显式推导出来。设 $U$ 是一个偶数维的向量空间，并且其双线性型非奇异，判别式为 $d$；再设 $V$ 是另一个带有二次型的向量空间。则有： $$ \operatorname{Cl}(U + V) \;\cong\; \operatorname{Cl}(U) \otimes \operatorname{Cl}\!\Bigl(\,(-1)^{\dim(U)/2} d V \Bigr),~ $$ 其中 $(-1)^{\dim(U)/2} d V$ 表示将 $V$ 的二次型整体乘以 $(-1)^{\dim(U)/2} d$。

　　 在实数情形下，这一结果特别意味着： $$ \operatorname{Cl}_{p+2,\,q}(\mathbf{R}) \;\cong\; M_2(\mathbf{R}) \otimes \operatorname{Cl}_{q,\,p}(\mathbf{R}),~ $$ $$ \operatorname{Cl}_{p+1,\,q+1}(\mathbf{R}) \;\cong\; M_2(\mathbf{R}) \otimes \operatorname{Cl}_{p,\,q}(\mathbf{R}),~ $$ $$ \operatorname{Cl}_{p,\,q+2}(\mathbf{R}) \;\cong\; \mathbf{H} \otimes \operatorname{Cl}_{q,\,p}(\mathbf{R}),~ $$ 其中 $M_2(\mathbf{R})$ 表示 $2 \times 2$ 实矩阵代数，$\mathbf{H}$ 表示四元数代数。这些公式可以用于求出所有实克利福德代数与复克利福德代数的结构；详见克利福德代数的分类。

　　 尤其需要指出的是，克利福德代数的 Morita 等价类（即其表示论意义下的模范畴等价类）仅依赖于其符号型差 $(p - q) \bmod 8$。这正是 Bott 周期性的一种代数形式。

9. 李普希茨群

　　 李普希茨群（Lipschitz group，又称 克利福德群 或 克利福德–李普希茨群，\(^\text{[11]}\)）由 鲁道夫·李普希茨发现。\(^\text{[12]}\)

　　 在本节中，我们假设 $V$ 是有限维向量空间，且二次型 $Q$ 非退化。

　　 克利福德代数的单位群可以通过扭曲共轭作用作用在代数元素上：由 $x$ 的扭曲共轭将 $y \;\mapsto\; \alpha(x)\, y\, x^{-1}$,其中 $\alpha$ 是前文定义的主对合。

　　 李普希茨群 $\Gamma$ 定义为在此作用下稳定向量空间 $V$ 的所有可逆元的集合 \(^\text{[13]}\)，即对任意 $v \in V$ 有： $$ \alpha(x) v x^{-1} \in V.~ $$ 该公式同时定义了李普希茨群在向量空间 $V$ 上的一个作用，并保持二次型 $Q$。因此，它给出了从李普希茨群到正交群的一个同态。李普希茨群包含所有满足 $Q(r)$ 在 $K$ 中可逆的向量 $r \in V$，这些元素作用在 $V$ 上时对应于反射：$v \;\mapsto\; v - \langle r, v \rangle + \langle v, r \rangle/Q(r)\, r$.（在特征为 2 的情形下，这些变换称为正交平移而非反射。）

　　 若 $V$ 是一个有限维实向量空间并带有非退化二次型，则根据 Cartan–Dieudonné 定理，李普希茨群在 $V$ 的正交群上是满射，其核由域 $K$ 的所有非零元组成。这导出以下正合列： $$ 1 \;\longrightarrow\; K^{\times} \;\longrightarrow\; \Gamma \;\longrightarrow\; \operatorname{O}_V(K) \;\longrightarrow\; 1,~ $$ $$ 1 \;\longrightarrow\; K^{\times} \;\longrightarrow\; \Gamma^{0} \;\longrightarrow\; \operatorname{SO}_V(K) \;\longrightarrow\; 1.~ $$ 在其他域或不定型的情形下，上述同态一般不是满射，其偏差由旋量范数来刻画。

旋量范数

　　 在任意特征下，旋量范数 $Q$ 定义在李普希茨群上： $$ Q(x) \;=\; x^{\mathrm{t}}x .~ $$ 它是从李普希茨群到域 $K$ 的非零元素群 $K^{\times}$ 的一个同态。当将 $V$ 视为克利福德代数的一个子空间时，该映射与 $V$ 上的二次型 $Q$ 一致。一些作者对旋量范数的定义略有不同，因此在 $\Gamma_{1}$ 上，它与此处的定义可能相差一个因子 $-1$、$2$ 或 $-2$。除了在特征 2 的情形外，这种差异并不重要。

　　 域 $K$ 的非零元素在旋量范数下的像属于群 $(K^{\times})^{2}$，即域 $K$ 中非零元素的平方所组成的群。因此，当 $V$ 是有限维且非奇异时，可以得到从 $V$ 的正交群到商群 $K^{\times}/(K^{\times})^{2}$ 的一个诱导映射，这个商群也称为旋量范数。关于任意向量 $r$ 的反射（即关于 $r^{\perp}$ 的反射），其旋量范数的像是 $Q(r)$ 在 $K^{\times}/(K^{\times})^{2}$ 中的元素，而这一性质唯一确定了旋量范数在正交群上的定义。于是我们得到以下正合列： $$ 1 \;\to\; \{\pm 1\} \;\to\; \operatorname{Pin}_{V}(K) \;\to\; \operatorname{O}_{V}(K) \;\to\; K^{\times}/(K^{\times})^{2},~ $$ $$ 1 \;\to\; \{\pm 1\} \;\to\; \operatorname{Spin}_{V}(K) \;\to\; \operatorname{SO}_{V}(K) \;\to\; K^{\times}/(K^{\times})^{2}.~ $$ 注意：在特征 2 的情况下，群 $\{\pm 1\}$ 只有一个元素。

　　 在代数群的伽罗瓦上同调视角下，旋量范数是上同调中的一个连接同态。记 $\mu_{2}$ 为代数群 “平方根为 1 的元素”（在特征不为 2 的域上，它与一个带平凡伽罗瓦作用的二元群大致相同），则短正合列 $$ 1 \;\to\; \mu_{2} \;\to\; \operatorname{Pin}_{V} \;\to\; \operatorname{O}_{V} \;\to\; 1~ $$ 导出一个上同调的长正合列，其开头部分为： $$ 1 \;\to\; H^{0}(\mu_{2}; K) \;\to\; H^{0}(\operatorname{Pin}_{V}; K) \;\to\; H^{0}(\operatorname{O}_{V}; K) \;\to\; H^{1}(\mu_{2}; K).~ $$ 这里：代数群 $G$ 在 $K$ 上的第 0 阶伽罗瓦上同调群就是其 **$K$-值点群**，即 $H^{0}(G; K) = G(K)$。而 $H^{1}(\mu_{2}; K) \cong K^{\times}/(K^{\times})^{2}$。 这正好复现了前述的正合列： $$ 1 \;\to\; \{\pm 1\} \;\to\; \operatorname{Pin}_{V}(K) \;\to\; \operatorname{O}_{V}(K) \;\to\; K^{\times}/(K^{\times})^{2},~ $$ 其中，旋量范数就是连接同态 $H^{0}(\operatorname{O}_{V}; K) \;\to\; H^{1}(\mu_{2}; K)$.

10. 旋量群与 Pin 群

　　 在本节中，我们假设 $V$ 是有限维的，并且其双线性型是非奇异的。

　　 Pin 群 $\operatorname{Pin}_{V}(K)$ 定义为 Lipschitz 群 $\Gamma$ 中旋量范数为 1 的子群。类似地，Spin 群 $\operatorname{Spin}_{V}(K)$ 定义为 $\operatorname{Pin}_{V}(K)$ 中 Dickson 不变量为 0 的子群。在特征不为 2 的情况下，它们就是行列式为 1 的元素。通常，Spin 群在 Pin 群中具有指数 2。

　　 回顾上一节，存在从 Lipschitz 群到正交群的同态。我们定义特殊正交群为 $\Gamma^{0}$ 的像。如果 $K$ 的特征不为 2，这就是正交群中行列式为 1 的元素所成的群。如果 $K$ 的特征为 2，那么正交群的所有元素行列式都为 1，此时特殊正交群定义为 Dickson 不变量为 0 的元素集合。

　　 存在从 Pin 群到正交群的同态。其像由旋量范数为 $1 \in K^{\times}/(K^{\times})^{2}$ 的元素组成。其核为 $\{+1,-1\}$，除非 $K$ 的特征为 2，否则这个核的阶为 2。类似地，存在从 Spin 群到 $V$ 的特殊正交群的同态。

　　 在常见的情形下，若 $V$ 是实数域上的正定或负定空间，则 Spin 群映射到特殊正交群，并且当 $\dim V \geq 3$ 时它是单连通的。此外，该同态的核是 $\{1,-1\}$。因此在这种情况下，Spin 群 $\operatorname{Spin}(n)$ 是 $\operatorname{SO}(n)$ 的二重覆盖。

　　 然而要注意：Spin 群的单连通性并非一般成立。例如当 $V = \mathbf{R}^{p,q}$ 且 $p, q \geq 2$ 时，Spin 群不是单连通的。在这种情况下，代数群 $\operatorname{Spin}_{p,q}$ 作为一个代数群是单连通的，但其实值点群 $\operatorname{Spin}_{p,q}(\mathbf{R})$ 却不是单连通的。这是一个相当微妙的点，至少有一本关于 Spin 群的标准著作在这一点上产生了严重混淆。

11. 旋量

　　 复 Clifford 代数 $\mathrm{Cl}_{p,q}(\mathbf{C})$，当 $p+q = 2n$ 为偶数时，是矩阵代数，并且具有维数为 $2^{n}$ 的复表示。将其限制到群 $\operatorname{Pin}_{p,q}(\mathbf{R})$，就得到一个同维数的 Pin 群复表示，称为旋量表示。如果进一步限制到旋量群 $\operatorname{Spin}_{p,q}(\mathbf{R})$，那么它会分裂为两个维数为 $2^{n-1}$ 的半旋量表示（half spin representations，也称 Weyl 表示）。

　　 若 $p+q = 2n+1$ 为奇数，则 Clifford 代数 $\mathrm{Cl}_{p,q}(\mathbf{C})$ 是两个矩阵代数的直和，每个代数都具有维数为 $2^{n}$ 的表示，并且它们同样都是 Pin 群 $\operatorname{Pin}_{p,q}(\mathbf{R})$ 的表示。将其限制到旋量群 $\operatorname{Spin}_{p,q}(\mathbf{R})$ 时，它们变得同构，因此旋量群拥有一个维数为 $2^{n}$ 的复旋量表示。

　　 更一般地说，任意域上的旋量群与 Pin 群也具有类似的表示，其具体结构取决于相应 Clifford 代数的结构：每当 Clifford 代数有一个因子是某个除环上的矩阵代数时，就会在该除环上得到相应的 Pin 群和 Spin 群的表示。关于实数情形的例子，可参见旋量相关条目。

实旋量

　　 为了描述实旋量表示，必须了解旋量群（Spin 群）在其 Clifford 代数中的位置。Pin 群 $\operatorname{Pin}_{p,q}$ 定义为 Clifford 代数 $\mathrm{Cl}_{p,q}$ 中所有可逆元素的集合，这些元素可以表示为单位向量的积： $$ \mathrm{Pin}_{p,q} = \{ v_1 v_2 \cdots v_r \mid \forall i, \ \|v_i\| = \pm 1 \}.~ $$ 与前文所给的 Clifford 代数的具体实现相比较，Pin 群对应于任意多个反射的乘积：它是整个正交群 $\operatorname{O}(p,q)$ 的覆盖。旋量群（Spin 群）由 Pin 群中那些 由偶数个单位向量乘积构成的元素组成。因此，根据 Cartan–Dieudonné 定理，$\operatorname{Spin}$ 是正规旋转群 $\operatorname{SO}(p,q)$ 的覆盖。

　　 设 $\alpha : \mathrm{Cl} \to \mathrm{Cl}$ 为一个自同构，其作用是对纯向量进行映射 $v \mapsto -v$。特别地，$\operatorname{Spin}_{p,q}$ 就是 Pin 群中在 $\alpha$ 作用下保持不变的子群。定义 $$ \mathrm{Cl}_{p,q}^{[0]} = \{ x \in \mathrm{Cl}_{p,q} \mid \alpha(x) = x \}.~ $$ （这些正好是 $\mathrm{Cl}_{p,q}$ 中偶次的元素。）于是旋量群包含在 $\mathrm{Cl}^{[0]}_{p,q}$ 中。

　　 $\mathrm{Cl}_{p,q}$ 的不可约表示限制后给出了 Pin 群的表示。反过来，由于 Pin 群是由单位向量生成的，它的所有不可约表示都可以以这种方式诱导出来。因此二者的表示是一致的。出于相同原因，旋量群的不可约表示与 $\mathrm{Cl}^{[0]}_{p,q}$ 的不可约表示完全一致。

　　 为了分类 Pin 表示，只需依赖于 Clifford 代数的分类。而要找到 Spin 表示（即偶子代数的表示），可以首先利用如下两个同构（见前文）： $$ \operatorname{Cl}^{[0]}_{p,q} \;\;\approx\;\; \operatorname{Cl}_{p,q-1}, \quad \text{当 } q > 0~ $$ $$ \operatorname{Cl}^{[0]}_{p,q} \;\;\approx\;\; \operatorname{Cl}_{q,p-1}, \quad \text{当 } p > 0~ $$ 由此，可以将 $(p,q)$ 型的 Spin 表示实现为 $(p, q-1)$ 或 $(q, p-1)$ 型的 Pin 表示。

12. 应用

微分几何

　　 外代数的主要应用之一在于微分几何，它被用来定义光滑流形上的微分形式丛。在（伪）黎曼流形的情形下，切空间天然配备了由度量诱导的二次型。因此，可以类似于外代数丛来定义 Clifford 丛。这一结构在黎曼几何中有许多重要应用。更为重要的是，它与 自旋流形、其相关的旋量丛 以及 Spin$^c$ 流形 之间存在紧密联系。

物理学

　　 Clifford 代数在物理学中有着大量重要的应用。物理学家通常将 Clifford 代数理解为由 狄拉克矩阵 $\gamma_0, \ldots, \gamma_3$ 生成的代数，它们满足如下关系： $$ \gamma_i \gamma_j + \gamma_j \gamma_i = 2 \eta_{ij},~ $$ 其中 $\eta$ 是一个二次型的矩阵，其指标为 $(1,3)$（或 $(3,1)$，对应于两种等价的度量符号选择）。这正是 Clifford 代数 $\mathrm{Cl}_{1,3}(\mathbf{R})$ 的定义关系，其复化 $\mathrm{Cl}_{1,3}(\mathbf{R})_{\mathbf{C}}$，根据 Clifford 代数的分类，同构于 $4 \times 4$ 复矩阵代数：$\mathrm{Cl}_{1,3}(\mathbf{R})_{\mathbf{C}} \;\cong\; \mathrm{Cl}_{4}(\mathbf{C}) \;\approx\; M_4(\mathbf{C})$.然而，最好仍然保留记号 $\mathrm{Cl}_{1,3}(\mathbf{R})_{\mathbf{C}}$，因为将双线性型转化为标准型的任何变换，并不是底层时空的洛伦兹变换。

　　 因此，物理学中所用的时空 Clifford 代数比 $\mathrm{Cl}_4(\mathbf{C})$ 具有更丰富的结构。它额外包含了一组优选的变换 —— 洛伦兹变换。至于是否一开始就需要进行复化，部分取决于所使用的记号习惯，部分取决于希望纳入多少数学结构。但在量子力学中，复化几乎总是必要的，因为位于 Clifford 代数中的李代数 $\mathfrak{so}(1,3)$ 的自旋表示，按照惯例需要复 Clifford 代数来实现。

　　 作为参考，自旋李代数由下式给出： $$ \sigma^{\mu\nu} = -\frac{i}{4}\,[\gamma^\mu,\, \gamma^\nu], ~ $$ $$ [\sigma^{\mu\nu},\, \sigma^{\rho\tau}] = i \big( \eta^{\tau\mu}\sigma^{\rho\nu} + \eta^{\nu\tau}\sigma^{\mu\rho} - \eta^{\rho\mu}\sigma^{\tau\nu} - \eta^{\nu\rho}\sigma^{\mu\tau} \big).~ $$ 这采用的是 $(3,1)$ 度量符号，因此对应于 $\mathrm{Cl}_{3,1}(\mathbf{R})_{\mathbf{C}}$\(^\text{[14]}\)。

　　 狄拉克矩阵最早由保罗·狄拉克写出，当时他正在尝试为电子建立一个相对论性的一级波动方程，并给出从 Clifford 代数到复矩阵代数的一个显式同构。这一成果被用来定义狄拉克方程并引入狄拉克算符。整个 Clifford 代数在量子场论中都会出现，以狄拉克场双线性形式的方式存在。

　　 Clifford 代数在量子理论中的应用由多位学者推动，包括 Mario Schönberg，\(^\text{[i]}\)David Hestenes（在几何演算的框架下），David Bohm 和 Basil Hiley 及其合作者（通过建立 Clifford 代数的层级结构），以及 Elio Conte 等人 \(^\text{[15][16]}\)。

计算机视觉

　　 Clifford 代数也被应用于计算机视觉中的动作识别与分类问题。Rodriguez 等人 \(^\text{[17]}\) 提出了一种 Clifford 嵌入，用来将传统的 MACH 滤波器推广到视频（3D 时空体积）和诸如光流之类的向量值数据。向量值数据通过 Clifford 傅里叶变换进行分析。在此基础上，动作滤波器在 Clifford 傅里叶域中被综合生成，动作识别则通过 Clifford 相关来完成。作者们通过识别经典电影片段和体育转播电视中的典型动作，展示了 Clifford 嵌入在动作识别中的有效性。

13. 推广

14. 参见

15. 注释

　　
a.也称为几何代数（尤其是在实数域上）。
b.参见例如 Oziewicz & Sitarczyk 1992。
c.一些研究实 Clifford 代数并偏好正定二次型的数学家（特别是研究指标理论的学者），有时在基本 Clifford 恒等式中使用不同的符号约定。即他们取 $v^{2} = -Q(v)$。在两种约定之间切换时，必须将 $Q$ 替换为 $-Q$。
d.Vaz & da Rocha (2016) 明确指出，映射 $i$（此处引文中的 $\gamma$）包含在 Clifford 代数的结构中，其定义为： “当代数 $A$ 由集合 $\{\gamma(v) \mid v \in V\}$ 和 $\{a1_{A} \mid a \in \mathbf{R}\}$ 所生成，且 $\gamma$ 满足对所有 $v,u \in V$，有 $\gamma(v)\gamma(u)+\gamma(u)\gamma(v)=2g(v,u)$， 则二元组 $(A,\gamma)$ 是二次空间 $(V,g)$ 的一个 Clifford 代数。”
e.因此，群代数 $K[\mathbf{Z}/2\mathbf{Z}]$ 是半单的，而 Clifford 代数会按照主对合的特征空间分解。
f.严格来说，如果没有指定的向量子空间，它并不具备完整的 Clifford 代数结构，因此只能作为代数同构，而不是作为 Clifford 代数同构。
g.我们依然假设特征不为 2。
h.当使用 Clifford 代数的另一种（−）符号约定时，情况正好相反：此时共轭（conjugate）比转置（transpose）更重要。一般而言，从一种符号约定切换到另一种时，共轭与转置的含义会互换。例如，在此处使用的约定下，向量的逆元由 $v^{-1} = v^{t} / Q(v)$ 给出，而在（−）约定下则为 $v^{-1} = v / Q(v)$。
i.关于 Schönberg 在 1956 和 1957 年的论文，可参见 Bolivar (2001) 的 “Grassmann–Schönberg 代数 $G_{n}$” 一节中的描述。
j.参见例如 Oziewicz & Sitarczyk 1992。

16. 引文

  1. Clifford 1873，第 381–395 页
  2. Clifford 1882
  3. Lounesto 1993，第 155–156 页
  4. Lounesto 1996，第 3–30 页，或节选版
  5. Lounesto 1993
  6. Lounesto 2001，§1.8
  7. Garling 2011，第 112 页
  8. Francis & Kosowsky 2005，第 404 页
  9. McCarthy 1990，第 62–65 页
  10. Bottema & Roth 2012
  11. Vaz & da Rocha 2016，第 126 页
  12. Lounesto 2001，§17.2
  13. Perwass 2009，§3.3.1
  14. Weinberg 2002
  15. Conte 2007
  16. Conte 2012
  17. Rodriguez & Shah 2008
  18. Haile 1984

17. 参考文献

18. 延伸阅读

19. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利