单位阶跃函数（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章

　　 海维赛德阶跃函数，又称单位阶跃函数，通常记作 $H$ 或 $\theta$ 有时也记作 $u$; 1 或 $\mathbb{1}$ 是一种以英国工程师奥利弗·海维赛德命名的阶跃函数。它在自变量为负时取值为 0 在自变量为正时取值为 1。关于函数在零点处的取值 $H(0)$ 存在不同的约定。该函数是阶跃函数类的一种典型代表，所有的阶跃函数都可以表示为它的平移的线性组合。

　　 这一函数最初出现在运算微积分中，用于求解微分方程。在该背景下，它表示一个在某一时刻 “打开” 并无限期保持 “打开” 的信号。海维赛德在分析电报通信时发展了运算微积分，并将该函数表示为 1。

1. 表述

　　 取约定 $H(0) = 1$，海维赛德函数可以定义为：

• 分段函数： $$ H(x) := \begin{cases} 1, & x \geq 0 \\[6pt] 0, & x < 0 \end{cases}~ $$
• 使用艾弗森括号记号： $$ H(x) := [x \geq 0]~ $$
• 作为示性函数： $$ H(x) := \mathbf{1}_{x \geq 0} = \mathbf{1}_{\mathbb{R}_{+}}(x)~ $$ 若取另一种约定 $H(0) = \tfrac{1}{2}$，则可以表示为：
• 分段函数： $$ H(x) := \begin{cases} 1, & x > 0 \\[6pt] \tfrac{1}{2}, & x = 0 \\[6pt] 0, & x < 0 \end{cases}~ $$
• 符号函数的线性变换： $$ H(x) := \tfrac{1}{2}\left(\operatorname{sgn}x + 1\right)~ $$
• 两个艾弗森括号的算术平均： $$ H(x) := \frac{[x \geq 0] + [x > 0]}{2}~ $$
• 双参数反正切函数（atan2）的单侧极限： $$ H(x) := \lim_{\epsilon \to 0^{+}} \frac{\operatorname{atan2}(\epsilon, -x)}{\pi}~ $$
• 作为超函数： $$ H(x) := \left( 1 - \frac{1}{2\pi i}\log z, \; -\frac{1}{2\pi i}\log z \right)~ $$ 或等价地： $$ H(x) := \left( -\frac{\log-z}{2\pi i}, \; -\frac{\log-z}{2\pi i} \right),~ $$ 其中 $\log z$ 表示复对数的主值。
  其它在 $H(0)$ 处未定义的形式包括：
• 分段函数： $$ H(x) := \begin{cases} 1, & x > 0 \\[6pt] 0, & x < 0 \end{cases}~ $$
• 斜坡函数（ramp function）的导数： $$ H(x) := \frac{d}{dx}\max\{x,0\}, \quad x \neq 0~ $$
• 用绝对值函数表示： $$ H(x) = \frac{x + |x|}{2x}~ $$

2. 与狄拉克 δ 函数的关系

　　 狄拉克 δ 函数是海维赛德函数的弱导数： $$ \delta(x) = \frac{d}{dx}\, H(x),~ $$ 因此，海维赛德函数可以被视为狄拉克 δ 函数的积分。有时写作： $$ H(x) := \int_{-\infty}^{x} \delta(s)\, ds,~ $$ 不过，对于 $x = 0$，这一展开式可能不成立（甚至无意义），这取决于采用哪种形式主义来定义涉及 $\delta$ 的积分。在这种语境下，海维赛德函数就是一个几乎必然为零的随机变量的累积分布函数（CDF）。（参见常量随机变量。）

3. 解析近似

　　 海维赛德阶跃函数的近似形式在生物化学和神经科学中很有用。例如，阶跃函数的逻辑近似，如 Hill 方程和米氏–曼腾方程，可用于模拟细胞在化学信号刺激下的二元开关反应。

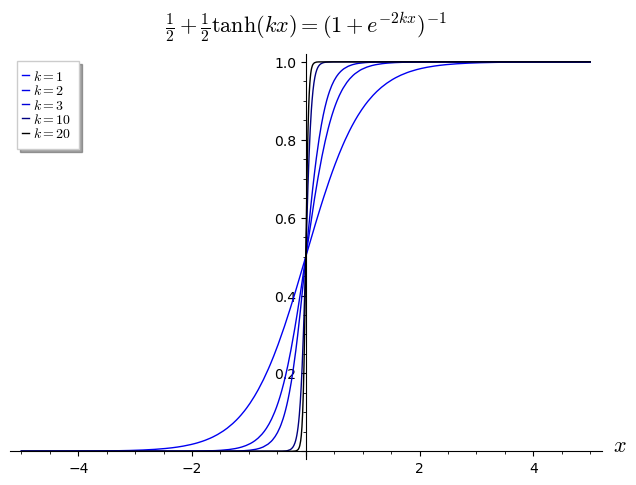
　　 对于阶跃函数的平滑近似，可以使用逻辑函数： $$ H(x) \approx \tfrac{1}{2} + \tfrac{1}{2}\tanh kx \;=\; \frac{1}{1 + e^{-2kx}},~ $$ 其中，$k$ 越大，则在 $x = 0$ 处的过渡越陡峭。

　　 如果取约定 $H(0) = \tfrac{1}{2}$，则在极限意义下成立： $$ H(x) = \lim_{k \to \infty} \tfrac{1}{2}\bigl(1 + \tanh kx\bigr) = \lim_{k \to \infty} \frac{1}{1 + e^{-2kx}}.~ $$

　　 阶跃函数还有许多其他平滑的解析近似形式。\(^\text{[1]}\) 其中一些可能性是： $$ \begin{aligned} H(x) &= \lim_{k \to \infty} \left( \tfrac{1}{2} + \tfrac{1}{\pi} \arctan\left(kx\right) \right) \\[6pt] H(x) &= \lim_{k \to \infty} \left( \tfrac{1}{2} + \tfrac{1}{2}\operatorname{erf}(kx) \right) \end{aligned}~ $$ 这些极限在逐点意义以及分布意义下都成立。然而，一般来说，逐点收敛并不必然意味着分布收敛，反之亦然。（不过，如果一个逐点收敛的函数序列中的所有函数都被某个 “良好” 的函数一致有界，那么其收敛也在分布意义下成立。）

　　 更一般地说，任何连续概率分布的累积分布函数（CDF），只要它在零点附近集中，并且带有一个可控方差的参数，在方差趋于零的极限下，都可以作为阶跃函数的近似。例如，上述三种近似函数分别是以下常见概率分布的累积分布函数：逻辑分布、柯西分布和正态分布。

4. 非解析近似

　　 海维赛德阶跃函数的近似也可以通过平滑过渡函数来实现，例如当 $1 \leq m \to \infty$ 时，定义函数： $$ f(x) = \begin{cases} \tfrac{1}{2}\Bigl(1 + \tanh\!\Bigl(m \tfrac{2x}{1 - x^{2}}\Bigr)\Bigr), & |x| < 1 \\[8pt] 1, & x \geq 1 \\[6pt] 0, & x \leq -1 \end{cases}~ $$

5. 积分表示

　　 海维赛德阶跃函数常常可以用积分表示： $$ \begin{aligned} H(x) &= \lim_{\varepsilon \to 0^{+}} -\frac{1}{2\pi i} \int_{-\infty}^{\infty} \frac{1}{\tau + i\varepsilon}\, e^{-ix\tau}\, d\tau \\[8pt] &= \lim_{\varepsilon \to 0^{+}} \;\frac{1}{2\pi i} \int_{-\infty}^{\infty} \frac{1}{\tau - i\varepsilon}\, e^{ix\tau}\, d\tau , \end{aligned}~ $$ 其中，第二个表示式可以很容易地从第一个推出，因为阶跃函数是实函数，因此它等于其自身的复共轭。

6. 零点处的取值

　　 由于 $H$ 通常用于积分，而函数在单点的取值并不会影响其积分，因此在大多数情况下，$H(0)$ 取何值并不重要。实际上，当 $H$ 被视为一个分布或 $L^{\infty}$ 空间（见 $L^p$ 空间）的元素时，讨论它在零点的具体取值甚至没有意义，因为这类对象只在 “几乎处处” 上定义。如果使用某种解析近似（如前面举的例子），那么通常会采用该近似在零点的极限值作为 $H(0)$。

　　 不同的取值选择有不同的理由：

• 取 $H(0) = \tfrac{1}{2}$：这样图像具有旋转对称性；换句话说，$H - \tfrac{1}{2}$ 是一个奇函数。在这种情况下，与符号函数的关系对所有 $x$ 成立： $$ H(x) = \tfrac{1}{2}\bigl(1 + \operatorname{sgn}(x)\bigr),~ $$ 并且 $\forall x,\; H(x) + H(-x) = 1$.
• 取 $H(0) = 1$：这种取法保证 $H$ 是右连续的。例如，累积分布函数（CDF）通常被定义为右连续的，勒贝格–斯蒂尔切斯积分中的被积函数也是右连续的。在这种情况下，$H$ 就是一个闭半无限区间的示性函数： $$ H(x) = \mathbf{1}_{[0,\infty)}(x).~ $$ 对应的概率分布是退化分布。
• 取 $H(0) = 0$：这种取法保证 $H$ 是左连续的。在这种情况下，$H$ 是开半无限区间的示性函数： $$ H(x) = \mathbf{1}_{(0,\infty)}(x).~ $$
• 在泛函分析、优化与博弈论的语境下：通常将海维赛德函数定义为一个多值函数，以保持极限函数的连续性并确保某些解的存在。在这种情况下，海维赛德函数在零点返回一个区间：$H(0) = [0,1]$.

7. 离散形式

　　 单位阶跃函数的另一种形式，可以定义为一个函数 $H : \mathbb{Z} \to \mathbb{R}$（即自变量是离散变量 $n$），定义为： $$ H[n] = \begin{cases} 0, & n < 0, \\[6pt] 1, & n \geq 0, \end{cases}~ $$ 或者使用半最大值约定： $$ H[n] = \begin{cases} 0, & n < 0, \\[6pt] \tfrac{1}{2}, & n = 0, \\[6pt] 1, & n > 0, \end{cases}~ $$ 其中 $n$ 为整数。若 $n$ 是整数，则 $n < 0$ 意味着 $n \leq -1$，而 $n > 0$ 则意味着函数在 $n = 1$ 时取到 1。因此，在采用半最大值约定时，这个所谓的 “阶跃函数” 在区间 $[-1,1]$ 上表现得更像是 “斜坡” 的行为，而不能严格意义上称为真正的阶跃函数。

　　 与连续情形不同，离散情形下 $H[0]$ 的定义是重要的。

　　 离散时间单位脉冲是离散时间阶跃函数的一阶差分： $$ \delta[n] = H[n] - H[n-1].~ $$ 该函数是克罗内克 δ 的累加和： $$ H[n] = \sum_{k=-\infty}^{n} \delta[k],~ $$ 其中 $\delta[k] = \delta_{k,0}$ 是离散单位脉冲函数。

8. 原函数与导数

　　 斜坡函数是海维赛德阶跃函数的一个原函数： $$ \int_{-\infty}^{x} H(\xi)\, d\xi = xH(x) = \max\{0, x\}.~ $$ 海维赛德阶跃函数的分布导数是狄拉克 δ 函数： $$ \frac{dH(x)}{dx} = \delta(x).~ $$

9. 傅里叶变换

　　 海维赛德阶跃函数的傅里叶变换是一个分布。在某一常见的傅里叶变换常数选择下，有： $$ \hat{H}(s) = \lim_{N \to \infty} \int_{-N}^{N} e^{-2\pi i x s} H(x)\, dx = \tfrac{1}{2}\left( \delta(s) - \tfrac{i}{\pi}\,\operatorname{p.v.}\frac{1}{s} \right).~ $$ 其中，$\operatorname{p.v.}\tfrac{1}{s}$ 是一个分布，它将测试函数 $\varphi$ 映射为以下积分的柯西主值：$\int_{-\infty}^{\infty} \frac{\varphi(s)}{s}\, ds$.积分中的极限同样是在（温和的）分布的意义下取的。

10. 单边拉普拉斯变换

　　 海维赛德阶跃函数的拉普拉斯变换是一个亚纯函数。采用单边拉普拉斯变换时，有： $$ \begin{aligned} \hat{H}(s) &= \lim_{N \to \infty} \int_{0}^{N} e^{-sx} H(x)\, dx \\[6pt] &= \lim_{N \to \infty} \int_{0}^{N} e^{-sx}\, dx \\[6pt] &= \frac{1}{s}. \end{aligned}~ $$ 当使用双边变换时，可以将积分拆分为两部分，结果仍然相同。

11. 参见

• 伽玛函数
• 狄拉克 δ 函数
• 示性函数
• 艾弗森括号
• 拉普拉斯变换
• 示性函数的拉普拉斯算子
• 数学函数列表
• 马考利括号
• 负数
• 矩形函数
• 符号函数
• 正弦积分
• 阶跃响应

12. 参考文献

1. Weisstein, Eric W. Heaviside Step Function. MathWorld.
2. Bracewell, Ronald Newbold (2000). The Fourier transform and its applications (第 3 版). New York: McGraw-Hill. p. 61. ISBN 0-07-303938-1.

13. 外部链接

• Digital Library of Mathematical Functions, NIST, [1].
• Berg, Ernst Julius (1936). “单位函数”. Heaviside's Operational Calculus, as applied to Engineering and Physics. McGraw-Hill Education. 第 5 页.
• Calvert, James B. (2002). “海维赛德、拉普拉斯与反演积分”. 丹佛大学.
• Davies, Brian (2002). “海维赛德阶跃函数”. Integral Transforms and their Applications (第 3 版). Springer. 第 28 页.
• Duff, George F. D.; Naylor, D. (1966). “海维赛德单位函数”. Differential Equations of Applied Mathematics. John Wiley & Sons. 第 42 页.