贡献者: certain_pineapple; addis
- 本文处于草稿阶段。
- 本文缺少预备知识,初学者可能会遇到困难。
- 注:本文中的自旋 $S$ 实际上为二倍的自旋,所以电子自旋被取值为 $\pm 1$,系数被吸纳入 $J$ 与 $B$ 中。
伊辛模型是用来描述铁磁现象的模型,其哈密顿量的形式为:
\begin{equation}
H=-J\sum\limits_{< i,j>}S_iS_j~.
\end{equation}
上式中的 $J$ 为交换耦合常数 $(J>0)$,$S_i$ 与 $S_j$ 是两原子的自旋,求和中的 $< i,j>$ 代表仅对最近邻的原子进行计算。
伊辛模型在一维和二维的情况下是可以严格求解的。在此介绍一维伊辛模型求解方法。
1. 一维伊辛模型求解
构建一维伊辛模型,并附以周期性边界条件,在外加磁场 $B$ 的情况下,模型的哈密顿量被写成:
\begin{equation}
H=-J\sum\limits_{i=1}^NS_iS_{i+1}-B\sum\limits_{i=1}^NS_i=-\sum\limits_{i=1}^N[JS_iS_{i+1}+B(S_i+S_{i+1})]~.
\end{equation}
上式中的 $BS_i$ 项中应为 $B\mu_i$,在此将玻尔磁子吸纳进 $B$ 的定义中。
写出配分函数:
\begin{align}
Z&=\sum\limits_{S_1,S_2,...S_N}exp\{\sum\limits_{i=1}^N\beta[JS_iS_{i+1}+B(S_i+S_{i+1})]\} \\
&=\sum\limits_{S_1,S_2,...S_N}\prod\limits_{i=1}^N exp\{\beta[JS_iS_{i+1}+B(S_i+S_{i+1})]\}~.
\end{align}
考虑:
\begin{equation}
\left\langle S_i \right\rvert P \left\lvert S_j \right\rangle =exp\{\beta[JS_iS_{j}+B(S_i+S_{j})]\}~,
\end{equation}
则有:
\begin{align}
Z&=\sum\limits_{S_1,S_2,...S_N}\prod\limits_{i=1}^N \left\langle S_i \right\rvert P \left\lvert S_i+1 \right\rangle \\
&=\sum\limits_{S_1,S_2,...S_N} \left\langle S_1 \right\rvert P \left\lvert S_2 \right\rangle \left\langle S_2 \right\rvert P \left\lvert S_3 \right\rangle \cdots \left\langle S_{N-1} \right\rvert P \left\lvert S_N \right\rangle ~.
\end{align}
考虑:
\begin{equation}
\sum_S \left\lvert S \right\rangle \left\langle S \right\rvert =\mathbb{1}~,
\end{equation}
则有:
\begin{equation}
Z=\sum\limits_{S_1} \left\langle S_1 \right\rvert P^N \left\lvert S_1 \right\rangle =tr(P^N)~.
\end{equation}
考虑 P 的矩阵元,由于 $S\in\{-1,1\}$,有:
$$P=\begin{pmatrix}
e^{\beta(J+B)},&e^{-\beta J} \\
~~e^{-\beta J}~~, & e^{\beta(J-B)}
\end{pmatrix}~.$$
计算得 $P$ 的本征值
$$\lambda=e^{\beta J}\cosh{(\beta B)}\pm \sqrt{e^{2\beta J }\sinh^2{(\beta B)}+e^{-2\beta J }}~.$$
则有:
\begin{align}
Z&=tr(P^N)=\lambda_1^N+\lambda_2^N \\~,
\lambda_1&=e^{\beta J}\cosh{(\beta B)}+ \sqrt{e^{2\beta J }\sinh^2{(\beta B)}+e^{-2\beta J }} \\~,
\lambda_2&=e^{\beta J}\cosh{(\beta B)}- \sqrt{e^{2\beta J }\sinh^2{(\beta B)}+e^{-2\beta J }}~.
\end{align}
则体系亥姆霍兹自由能 $F$:
$$F=-\beta^{-1}\ln{Z}=-\beta^{-1}\ln{(\lambda_1^N+\lambda_2^N)}=-N\beta^{-1}\ln{\lambda_1}-\beta^{-1}\ln[1+(\frac{\lambda_2}{\lambda_1})^N]~.$$
在通常情况下 $(B$ 和 $T$ 不全为 $0)$,有 $\lambda_1>\lambda_2$。所以在热力学极限下 $(N\rightarrow\infty)$,有:
$$F=-N\beta^{-1}\ln{\lambda_1}~.$$
可以求出平均自旋(此处 $B$ 包含玻尔磁子):
$$s=-\frac{1}{N}\frac{\partial F}{\partial B}=\frac{ \sinh\left(\beta B\right) }{\sqrt{\sinh^2(\beta B)+e^{-4\beta J}}}~.$$
绘制各种情况的图像。
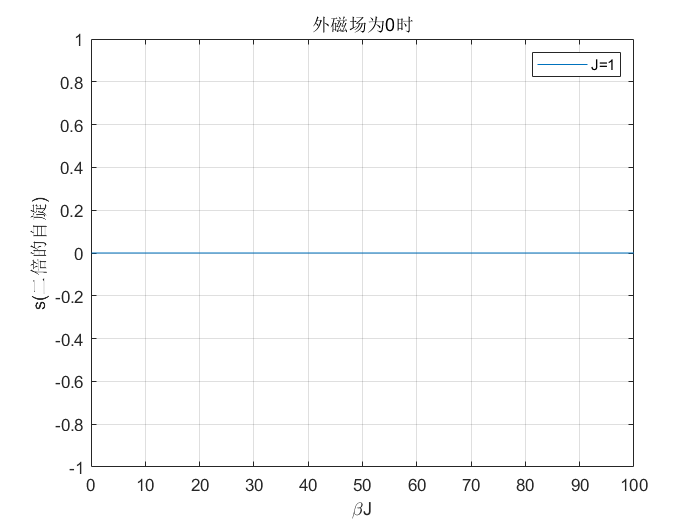
图 1:外磁场为 0 时
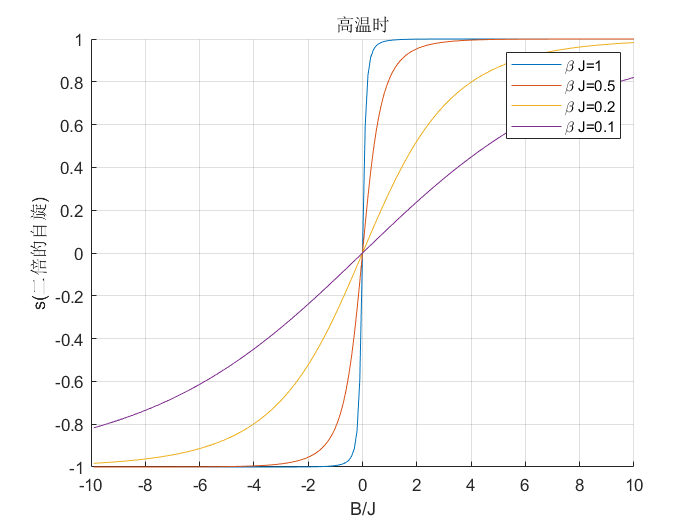
图 2:高温时
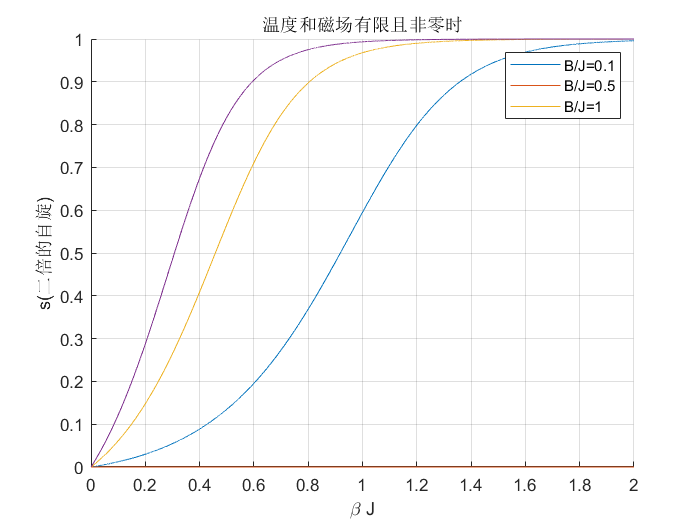
图 3:温度和磁场有限且非零时
横纵坐标的选取追求无量纲。
从图中可以看出,
在 $B\neq 0$ 时,$s$ 随温度连续变化。
在 $B=0$ 时,分两种情况,当 $T=0$ 时,$m$ 根据磁场趋向
于 0 的方向可分别取值 $\pm1$,当 $T\neq0$ 时,$s=0$。
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。