概率习题(高中)
贡献者: jingyuan
- 本文处于草稿阶段。
1. 例 1
(全国乙卷数学理 6)将 5 名北京奥运会志愿者分配到花样滑冰、短道速滑、冰球和冰壶 4 个项目进行培训,每名志愿者只分到 1 个项目,每个项目至少分配 1 名志愿者,则不同的分配方案共有()
A.60 种
B.120 种
C.240 种
D.480 种
解答:
由题,5 名运动员要分成 4 组,我们需要挑出两个人分为一组,其余一人一组
\begin{equation}
C_5^2 = 10 ~,
\end{equation}
再对四组进行全排
\begin{equation}
A_4^4 = 24~,
\end{equation}
\begin{equation}
C_5^2A_4^4 =240 ~.
\end{equation}
2. 例 2
(2020 年高考一卷 19)甲、乙、丙三位同学进行羽毛球比赛,约定赛制如下:
累计负两场者被淘汰;比赛前抽签决定首先比赛的两人,另一人轮空;每场比赛的胜者与轮空者进行下一场比赛,负者下一轮轮空,直至有一人被淘汰;当一人被淘汰后,剩余的两人继续比赛,直至其中一人被淘汰,另一人最终获胜,比赛结束。
经抽签,甲、乙首先比赛,丙轮空。设每场比赛双方获胜的概率都为 $\frac{1}{2}$.
(1) 求甲连胜四场的概率;
(2) 求需要进行第五场比赛的概率;
(3) 求丙最终获胜的概率。
解答:
(1)(第一问没有什么难度,注意答题格式规范)
设甲连胜四场为事件 $A$
\begin{equation}
P(A) = (\frac{1}{2})^4 = \frac{1}{16}~.
\end{equation}
图 1:图解 2-2
如图所示,进行 5 场比赛有两种情况,负者 1 胜一定进行 5 场,负者 1 负,有 $\frac{1}{2}$ 的概率进行五场
设进行 5 场比赛为事件 $B$
\begin{equation}
P(B) = \frac{1}{2} + \frac{1}{2} \cdot \frac{1}{2} = \frac{3}{4}~.
\end{equation}
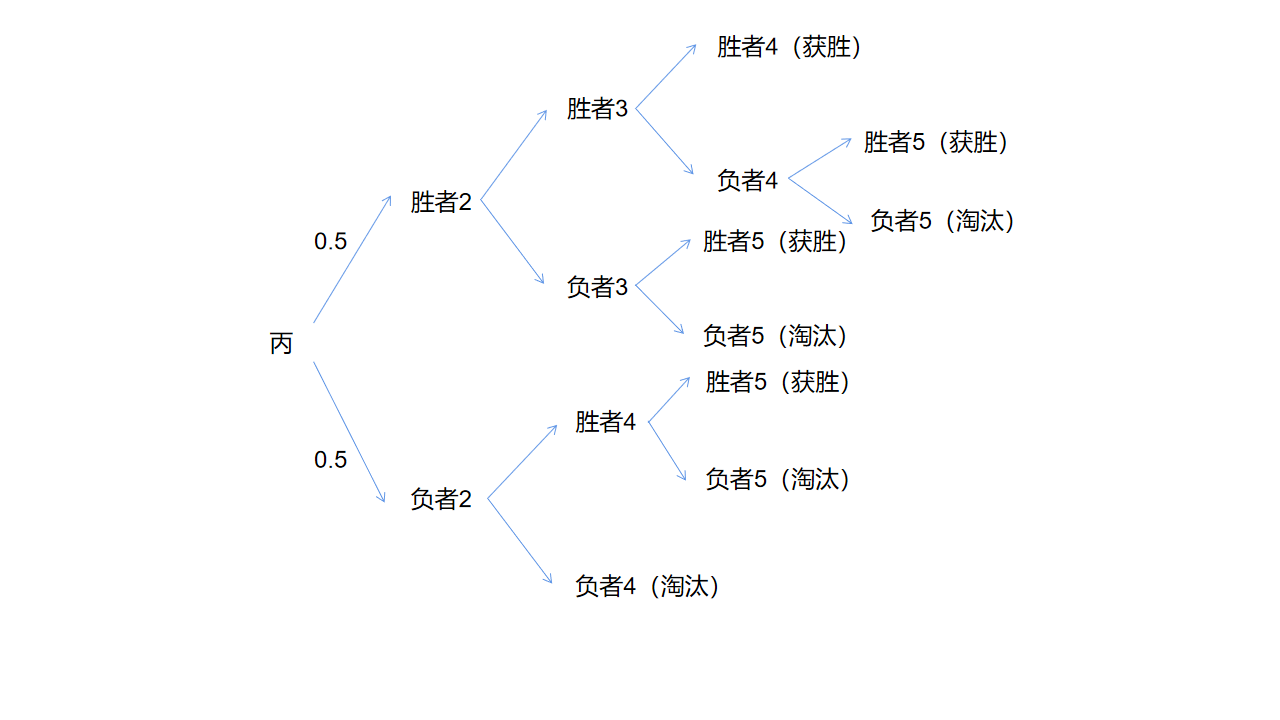
图 2:图解 2-3
设丙获胜为事件 $C$
由图可得
\begin{equation}
P(C) = (\frac{1}{2})^4 + (\frac{1}{2})^3 + (\frac{1}{2})^3 + (\frac{1}{2})^3 = \frac{7}{16}~.
\end{equation}
以上是编者的解法,网络上可以找到其他解法,这里插入一种作为参考
图 3:来自百度文库
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。
友情链接: 超理论坛 | ©小时科技 保留一切权利