曲线运动（高中）

贡献者： kahoyip; 叶月2_

1. 曲线运动

• 定义：轨迹是曲线的运动。
• 条件：当物体所受的合外力（加速度）与其速度方向不在同一直线上时，物体做曲线运动。
• 物体所受合外力方向（加速度方向）：总是指向曲线的凹侧。
• 速度方向：质点在某一位置的速度方向与曲线在这一点的切线方向一致。

2. 运动的合成与分解

　　 想象一下，物体在平面直角坐标系上运动，令它的运动轨迹表示为 $ \boldsymbol{\mathbf{r}} (t)=(x(t),y(t))$，每确定时刻 $t$，就确定了该物体的位置。如果我们把每个时刻物体的位置投影到 $x$ 轴或者 $y$ 轴，相当于该物体在对应轴上亦有一个运动，x 轴上物体作 $x(t)$ 这一直线运动，$y$ 轴上同理。于是，我们把投影结果称为物体的分运动，把投影过程称为运动的分解，把物体实际运动称为合运动，或言，是不同运动的合成。

　　 如果现在再给定一个运动轨迹 $ \boldsymbol{\mathbf{r}} _2(t)=(x_2(t),y_2(t))$，并进行叠加呢？也就是说，物体的真正轨迹为 $ \boldsymbol{\mathbf{r}} '(t)=(x_1+x_2,y_1+y_2)$。这种合成和分解显然基于矢量的可加性。比如 $x$ 轴上有两个运动，$x_1=5t,x_2=8t^2$，那么合运动就可以看作是速度为 $5\,m/s$ 的匀速直线运动与初速度为 $0$，加速度为 $16\,m/s^2$ 的匀加速直线运动所合成。

　　 运动是由力决定的，如果我们不知道物体的实际轨迹，仅知道初始条件和受力，那么可以根据牛顿定律进行运动的分解，从而得到物体的分运动。这是因为力与加速度都是矢量，一个合运动的牛顿定律 $ \boldsymbol{\mathbf{F}} =m \boldsymbol{\mathbf{a}} $，可以分解为比如 $x$ 轴和 $y$ 轴上的表达式，即 $ \boldsymbol{\mathbf{F}} _x=m \boldsymbol{\mathbf{a}} _x$ 和 $ \boldsymbol{\mathbf{F}} _y=m \boldsymbol{\mathbf{a}} _y$。

　　 常见的运动分解有以下几种：

1. (类)平抛运动 水平方向（任意方向）物体作匀速直线运动，竖直方向（垂直上述的 “任意方向”）物体作初速度为 $0$，加速度为 $ \boldsymbol{\mathbf{g}} $（其他加速度）的匀变速直线运动。(类)平抛运动的本质是给予物体某一初速度后，物体在垂直该速度方向只受恒力，在该恒力下作抛物线运动。平抛运动的分运动表达式为：
   \begin{equation} \begin{aligned} x&=v_0t,\\ y&=\frac{1}{2}gt^2~. \end{aligned} \end{equation}
   令 $t=x/v_0$，可得：$y=gx^2/(2v_0^2)$，因此，物体的合运动确为一抛物线。
2. 斜抛运动 给定物体某一斜向上的初速度，物体在重力作用下的运动。由分解可知，水平上物体由于不受力而作匀速直线运动，竖直方向上物体在重力作用下作竖直上抛运动。

3. 小船渡河问题

　　 小船渡河是学习运动的合成与分解时较为典型的问题。在具体分析前，我们先假设河宽为 $d$，小船在静水中的速度为 $ \boldsymbol{\mathbf{v}} _1$，小船静止随水漂流的速度为 $ \boldsymbol{\mathbf{v}} _2$。小船渡河实际运动就是小船在静水时的运动和随水漂流的运动的合运动，实际速度 $ \boldsymbol{\mathbf{v}} $ 就是小船在静水中的速度和随水漂流的速度的合速度。

　　 在小船渡河的过程中，如果任意时刻 $ \boldsymbol{\mathbf{v}} _1$ 和 $ \boldsymbol{\mathbf{v}} _2$ 都保持不变，那么船的实际速度 $ \boldsymbol{\mathbf{v}} $ 也对应地保持不变，此时船的实际运动就是匀速直线运动。由于 $ \boldsymbol{\mathbf{v}} _2$ 的方向是与河岸平行的，因此小船渡河的实际方向，就由船头的朝向即 $ \boldsymbol{\mathbf{v}} _1$ 的方向决定。如果 $ \boldsymbol{\mathbf{v}} _1$ 和 $ \boldsymbol{\mathbf{v}} _2$ 会随时间发生改变，那么船的实际运动就可能变成曲线运动。接下来我们只对第一种情况展开讨论。

　　 设 $ \boldsymbol{\mathbf{v}} _1$ 与 $ \boldsymbol{\mathbf{v}} _2$ 的夹角为 $\theta$，显然要渡河就必须有 $0^\circ < \theta < 180^\circ $，否则这个问题就变成了顺水、逆水行船问题。

最短渡河时间

　　 由于小船随水漂流的速度方向与河岸平行，因此这个速度并不会影响小船垂直于河岸方向的运动，因此小船在垂直于河岸方向的速度只与小船的静水速度有关。以沿河岸方向为 $x$ 轴以及垂直于河岸的方向为 $y$ 轴建立直角坐标系，设船的静水速度与垂直于河岸的方向夹角为 $\alpha$，则 $v_y = v_1 \cos \alpha$，渡河时间 $t=d/v_y$。由此可知，当 $\alpha = 0^\circ$，即船头方向垂直于河岸时，小船的实际速度在垂直河岸方向的分速度达到最大值 $v_1$，即船的静水速度全部用于渡河，此时渡河时间最短，$t_{min}=d/v_1$，实际速度大小 $v=\sqrt{v_1^2+v_2^2}$，对应渡河位移大小 $s=vt_{min}=\sqrt{v_1^2+v_2^2}\cdot d/v_1$。

最短渡河位移

　　 从平行线的关系来看，最短的渡河位移大小就是河宽，那是否任意的船速都能实现呢？以河宽为最短位移大小时，船的实际速度方向应垂直于河岸，则船头方向应偏向上游。根据三角形定则，此时 $v_1$、$v_2$ 和 $v$ 构成了以 $v_1$ 为斜边的直角三角形，在这个三角形中有 $v_1>v_2$。因此，在 $v_1>v_2$ 的情况下，小船渡河的最短位移大小等于河宽 $d$，小船的实际速度大小 $v=\sqrt{v_1^2-v_2^2}$，对应的渡河时间 $t=d/\sqrt{v_1^2-v_2^2}$。

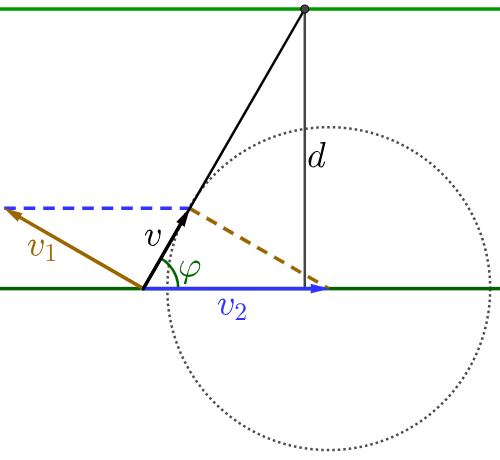
　　 当 $v_1< v_2$ 时，船无法垂直于河岸运动，此时无论船头方向如何，小船的实际运动方向总是偏向下游，设小船的实际速度与水流方向的夹角为 $\varphi$，则渡河位移 $s = d/\sin \varphi$，要使位移最小，则 $\varphi$ 要达最大值。如 图 2 所示，以水流速度矢量的末端为圆心，船的静水速度大小为半径作圆，可以发现，当实际速度与圆相切，即 $v_1$、$v_2$ 和 $v$ 构成了以 $v_2$ 为斜边的直角三角形时，$\varphi$ 角有最大值，$\varphi= \arcsin\left(v_1/v_2\right) $，此时小船的实际速度大小 $v=\sqrt{v_2^2-v_1^2}$，最短渡河位移大小 $s_{min} = d/\sin \varphi=dv_2/v_1$。

　　 通常，关于小船渡河问题的最短位移的讨论不会提及 $v_1=v_2$ 的情况，因为这种情况下只能结合极限的概念得出一个趋近的数值。此处简单地分析一下：当 $v_1=v_2$，小船的实际速度与水流方向的夹角为 $\theta /2$，实际速度大小 $v=2v_2 \cos\left(\theta /2\right) $，渡河位移大小 $s= d/ \sin\left(\theta/2\right) $，由于 $0^\circ < \theta < 180^\circ $，可见 $\theta$ 越大渡河位移越小，因此 $\theta$ 趋近于 $180^\circ $ 时，渡河位移大小趋近于 $d$，而实际速度大小趋于 $0$，行船时间则趋于无穷大。

4. 抛体运动

　　 将物体以一定的初速度 $ \boldsymbol{\mathbf{v}} _0$ 向空中抛出，物体在仅受重力作用的情况下所做的运动叫做抛体运动。根据抛出的方向不同，抛体运动可分为竖直上抛运动、竖直下抛运动、平抛运动和斜抛运动，其中平抛运动和斜抛运动属于曲线运动。

　　 抛体运动是一种把物体看作质点、仅考虑重力作用（忽略了空气阻力）的理想化模型。

　　 分析抛体运动时，通常会以水平方向为 $x$ 轴，竖直方向为 $y$ 轴建立直角坐标系将其分解为水平方向上的匀速直线运动和竖直方向上的匀变速直线运动。

平抛运动

　　 初速度 $v_0$ 沿水平方向的抛体运动叫做平抛运动。进行分析时可将平抛运动分解为沿水平方向（$x$ 轴）的匀速直线运动以及沿竖直方向（$y$ 轴）的自由落体运动。具体分析前我们先规定初速度的方向为 $x$ 轴的正方向，竖直向下的方向为 $y$ 轴的正方向。

• 平抛运动在 $t$ 时刻的水平方向速度 $v_x$ 和竖直方向速度 $v_y$：
  \begin{equation} v_x=v_0,\qquad v_y=gt~. \end{equation}
  实际速度大小：
  \begin{equation} v=\sqrt{v_x^2+v_y^2}~. \end{equation}
• 平抛运动在 $t$ 时刻的水平方向位移 $x$ 和竖直方向位移 $y$：
  \begin{equation} x=v_0t~, \end{equation}
  \begin{equation} y=\frac12 gt^2~. \end{equation}
  实际位移大小：
  \begin{equation} s=\sqrt{x^2+y^2}~. \end{equation}
• 联立式 4 和式 5 消去 $t$ 可得
  \begin{equation} y=\frac{g}{2v_0^2}x^2~, \end{equation}
  由此可知平抛运动的轨迹是抛物线。
• 当物体从高度为 $h$ 处被抛出时，下落时间
  \begin{equation} t=\sqrt{\frac{2h}{g}}~, \end{equation}
  可见物体在空中的飞行时间仅取决于下落的高度 $h$。
• 落地的水平距离
  \begin{equation} x=v_0\sqrt{\frac{2h}{g}}~. \end{equation}
  落地的瞬时速度
  \begin{equation} v=\sqrt{v_0^2+2gh}~. \end{equation}
  可见物体落地时的水平位移和瞬时速度都只与初速度 $v_0$ 和下落高度 $h$ 有关。
• 对于速度方向与水平方向的夹角 $\alpha$ 有：
  \begin{equation} \tan \alpha = \frac {v_y}{v_x}=\frac{gt}{v_0}~. \end{equation}
  对于位移方向与水平方向的夹角 $\beta$ 有：
  \begin{equation} \tan \beta = \frac{y}{x}=\frac{\frac12 gt^2}{v_0t} = \frac{gt}{2v_0}~. \end{equation}
  结合式 11 和式 12 可知，做平抛（或类平抛）运动的物体，在其运动过程中的任意时刻，其速度偏向角的正切值等于位移偏向角正切值的 $2$ 倍。由此结合几何知识可进一步证明，在任意时刻的瞬时速度的反向延长线一定交于水平位移的中点。

斜抛运动

　　 初速度 $v_0$ 沿斜向上或斜向下方向的抛体运动叫做斜抛运动。此处以斜上抛运动为例，可以将其分解为沿水平方向（$x$ 轴）的匀速直线运动以及沿竖直方向（$y$ 轴）的竖直上抛运动，设初速度 $v_0$ 与水平方向的夹角为 $\theta$，并规定两个分运动的初始方向为竖直、水平的正方向。

• 斜上抛运动在 $t$ 时刻的水平方向速度 $v_x$ 和竖直方向速度 $v_y$：
  \begin{equation} v_x=v_0\cos\theta~, \end{equation}
  \begin{equation} v_y=v_0\sin\theta-gt~. \end{equation}
• 斜上抛运动在 $t$ 时刻的水平方向位移 $x$ 和竖直方向位移 $y$：
  \begin{equation} x=v_0t\cos\theta~, \end{equation}
  \begin{equation} y= v_0t\sin\theta-\frac12 gt^2~. \end{equation}
• 当抛出点和落地点在同一水平面时，运动时间
  \begin{equation} t=\frac{2v_0\sin\theta}{g}~. \end{equation}
  射高
  \begin{equation} h=\frac{v_o^2\sin^2\theta}{2g}~. \end{equation}
  射程
  \begin{equation} s=v_0t\cos\theta=\frac{v_0^2\sin{2\theta}}{g}~. \end{equation}
  可见，运动时间和射高都随 $\theta$ 增大而增大，当 $\theta=45^\circ$ 时射程最大。
• 联立式 15 和式 16 消去 $t$ 可得
  \begin{equation} y=\tan\theta\cdot x-\frac{g}{2v_0^2\cos^2\theta}\cdot x^2~. \end{equation}
  由此可知斜上抛运动的轨迹是抛物线。
• 在实际情况中，由于不能忽略空气阻力的影响，斜抛运动的实际运动轨迹并不是理论计算出来的抛物线，这个实际运动轨迹叫做弹道曲线。