华东师范大学 2015 年硕士研究生物理考试试题

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

　　 普适气体常量 $R=8.31 J/(mol.k)$，玻尔兹曼常量 $k=1.38*10^{-23}$ , 电子质量 $m_4=9.11*10^{-31}$, 真空介电常量 $\varepsilon_0=8.85*10^{-12}C^2.N^{-1}$ , 普朗克常量 $h=6.63*10^{-34}$

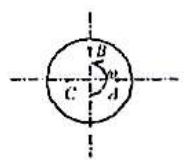
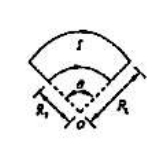
1. 如图所示，一圆盘绕通过其中心且垂直于盘面的转轴，以角速度 $\omega$ 作定轴转动，$A,B,C$ 三点与中心的距离均为 $r$。则图示 $A,B$ 点速度差 $\bar v_{AB}=\bar v_A-\bar v_B$ 与 $A,C$ 点的速度差 $\bar v_{AC}=\bar v_A-\bar v_C$ 的关系为 $(\qquad)$
   (A)$\bar v_{AB}>\bar v_{AC}$
   (B)$\bar v_{AB}<\bar v_{AC}$
   (C)$\bar v_{AB}=\bar v_{AC}$
   (D)$ \left\lvert \bar v_{AB} \right\rvert = \left\lvert \bar v_{AC} \right\rvert $
   
   图 1
2. 题 1 中，如果圆盘的质量为 $M$，在 $A$ 点处有一个质量为 $m$ 的人。刚开始人和圆盘相对于地面均处于静止状态。当人沿着圆盘走一圈时，圆盘相对于地面转过的角度为 $(\qquad)$
   (A)$\displaystyle \frac{4\pi m}{2m+M}$
   (B)$\displaystyle \frac{2\pi m}{2m+M}$
   (C)$\displaystyle \frac{2\pi m}{m+M}$
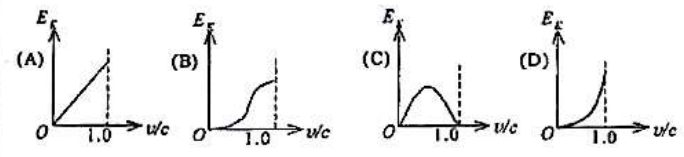
   (D)$0$
3. 令电子的速率为 $v$，则电子的动能 $E_x$ 对于比值 v/c 的图线可用下列图中哪一个图表示?(c 表示真空中光速)
   
   
   图 2
4. 一质点沿螺旋线状的曲线自外向内运动，如图所示、已知其走过的弧长与时间的一次方成正比。则该运动为 $(\qquad)$
   (A)加速度值越来越小的匀速率曲线运动
   (B)加速度值越来越大的匀速率曲线运动
   (C)加速度值越来越小的变速率曲线运动
   (D)加速度值越来越大的变速率曲线运动
   
   图 3
5. 质量分别为 $m_A$ 和 $m_B (m_A>m_B)$、速度分别为和的两质点 $A$ 和 $B$，受到相同的冲量作用,则 $(\qquad)$
   (A)$A$ 的动量增量的绝对值比 $B$ 的小
   (B)$A$ 的动量增量的绝对值比 $B$ 的大
   (C)$A,B$ 的动盘增量相等
   (D)$A,B$ 的速度增量相等
6. 老师和学生各带一个钟。他们在长沙站对好钟(显示是同一时刻)，学生就坐上火车往武汉去。如果考虑到相对论效应，当学生到达武汉后，他的钟与老师的钟相比，哪一个会变慢？设同一参考系的钟都是同步的。
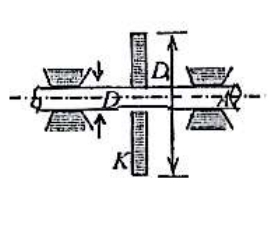
7. 如图所示，一圆盘形工件 K 套装在一根可绕自身轴线转动的固定轴 $A$ 上，圆盘 K 的中心线与固定轴 A 的中轴线互相重合，圆盘的内外直径分别为 $D$ 和 $D_1$，该工件在外力矩作用下获得角速度 $\omega_0$ 这时撤掉外力矩，工件在轴所受的阻力矩作用下最后停止转动，其间经过了时间 t，则轴所受的平均阻力为 $(\qquad)$，这里圆盘工件绕其中心轴转动的转动惯量为 $m(D^2+D^2_1)/8$，$m$ 为圆盘的质量，轴的转动惯量忽略不计。
   
   图 4
8. 一质点在二恒力共同作用下，位移为 $\Delta F=3\bar i +8\bar j \quad$ (SI):在此过程中，动能增量为 $24J$，已知其中一恒力 $\bar F_1$=$12 \bar i-3 \bar j$(SI)，则另一恒力所作的功为 $(\qquad)$
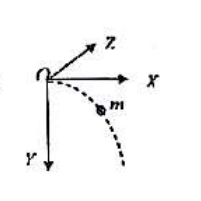
9. 如图所示，$x$ 轴沿水平方向，$y$ 轴竖直向下，$z$ 轴垂直于纸面向内，在 $t=0$ 时刻将质量为 $m$ 的质点以初速度 $\bar v_0$ 从参考点平抛出去，则在任意时刻 $t$ 质点所受的对原点 $O$ 的力矩为 $(\qquad)$。
   
   图 5
10. 质心参考系的特点是 $(\qquad)$。
11. 质量一定的理想气体，从相同状态出发，分别经历等温过程，等压过程和绝热过程，使其体积增加一倍，那么气体温度的改变(绝对值) $(\qquad)$
    (A)绝热过程中最大，等压过程中最小
    (B)绝热过程中最大，等温过程中最小
    (C)等压过程中最大，绝热过程中最小
    (D)等压过程中最大，等温过程中最小
12. 一物质系统从外界吸收一定的热量，则 $(\qquad)$。 (A)系统的内能一定增加 (B)系统的内能一定减少 (C)系统的内能一定保持不变 (D)系统的内能可能增加，也可能减少或保持不变
13. 刚性三原子分子理想气体的压强为 $P$，体积为 $V$,则它的内能 $(\qquad)$
    (A) $2PV$ (B) $PV$ (C)$3PV$ (C)$4.5PV$
14. 一瓶氢气和一瓶氦气气体密度相同，分子的平均平动能相同，而且它们都处于平衡状态，则它们 $(\qquad)$
    (A)温度相同，压强相同
    (B)温度，压强都不相同
    (C)温度相同，但氦气的压强大于氢气的压强
    (D)温度相同，但氢气的压強大于氦气的压强
15. 设高温热源的热力学温度是低温热源的热力学温度的 n 倍，则理想气体在一次卡诺循环中，传给低温热源的热最是从高温热源吸取热量的 $(\qquad)$
    (A)$n$ 倍
    (B)$n-1$ 倍
    (C) $\frac{1}{n}$ 倍
    (C)$\frac{n+1}{n}$ 倍
16. 用一个隔板把绝热容器分成体积为 $V_1$ 和 $V_2$ 两部分,两部分初始温度均为 T，初始压强均为 P.但所盛气体种类不同，若将隔板抽开，让气体均匀混合，求混合前后系统的熵变 $\Delta S$ = $(\qquad)$
17. 一定量的某种理想气体在等压过程中对外做功为 $200J$，若此种气体为单原子分子气体，则该过程中需吸收的热量是 $(\qquad)$,若此种气体为双原子分子气体，则该过程中吸收的热盘是 $(\qquad)$。
18. 水蒸汽分解为同温度的氢气和氧气。气体的内能增加百分比为 $(\qquad)$。
19. 一飞机在地面时机舱中的压力指示为 $1.01*10^5 Pa$，到高空后压强降为 $8.11*10^4 Pa$,设大气温度均为 27 度，问此时飞机距地面的高度为 $(\qquad)$(设空气的摩尔质量为 $2.89*10^{-2}Kg/mol$)。
20. 一绝热密封容器体积为 $V=10^{-2}m^3$，以速度 $v=100m/s$ 作匀速直线运动。容器中有 $100g$ 氢气，当容器突然停止时，氢气的温度增加量 $\Delta T=(\qquad)$。
21. 自然光入射光强为 I,,通过两个尼科耳棱镜。当两个尼科耳棱镜主截面的夹角由 45°减小为 30°时，试问透射光强的变化 $(\qquad)$
    (A)增大
    (B)减小
    (C)不变
    (D)不能确定
22. 菲涅耳圆孔衍射实验中，对轴上某参考点圆孔刚好露出 $\frac{3}{2}$ 个半波带时，该点的光强度与自由传播时的之比为 $(\qquad)$
    (C)$1:2$
    (D)$2:1$
    (A)$1:\sqrt{2}$
    (B)$\sqrt{2}:1$
23. 在白光照射下，夫琅禾费衍射的零级斑正中心是什么颜色的 $(\qquad)$
    (A)白色
    (B)红白色
    (C)蓝白色
    (D)彩色
24. 将一偏振片沿 45°角插入一对正交的偏振器之间。当有一束自然光经过它们的时候，求出射光强与入射光强的比值 $(\qquad)$
    (A)1:2
    (B)1:4
    (C)1:8
    (D)1:16
25. 当你用一台望远镜去观察双星现象，发现很难分辨出它们。你决定插入一个滤光器来最大化它的分辨率。试问你会选择什么颜色的滤光器 $(\qquad)$
    (A)红色
    (B)绿色
    (C)黄色
    (D)蓝色
    
26. 波长为 6500A 的红光谱线，经过观测发现它是双线的。在该红光下调节迈克尔逊干涉仪，人们发现干涉场的反衬度随镜面移动而周期性变化。实测的结果由条纹清晰到最模糊，视场中吞(吐)$1.35$x$10^5$ 圈条纹。试写出该红光双线的两个波长分别是 $(\qquad)$ 和 $(\qquad)$。
27. 试计算水面波的群速度 $(\qquad)$,已知相速 $\displaystyle v_p=\sqrt{\frac{\lambda}{2\pi}(g+\frac{4\pi ^2 T}{\lambda^2 \rho})}$,$g$ 为重力加速度，$T$ 为表面张力，$\rho$ 为波体的密度。
28. 热核爆炸中火球的瞬时温度高达 $10^7$K，则辐射最强的波长是 $(\qquad)$(已知维恩常致 b=$2.898$x$10^{-3}$mK)
29. 要产生明显的康静顿散射效应，能否用可见光来完成？$(\qquad)$(填可以或不可以):试解释原因 $(\qquad)$。
30. 太阳能电池是一类在太阳光照射下能够发电的新材料。太阳能电池的表面通常被镀上一层透明的氧化硅薄膜($Si0,n=1.45$)用于减小表面反射的损耗，若硅电池层的折射率为 $n=3.5$，试求能够实现反射光波长达到 $550nm$ 的最小薄膜厚度 $(\qquad)$。
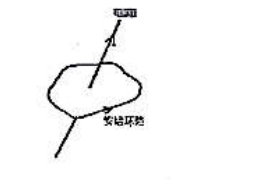
31. 如图所示，电流 $I$ 与形状不规则的安培回路平面的夹角为 $\theta$ 规定安培回路的绕行方向为逆时针,则 $\oint \vec B.d\vec l$ 的值为多少？$(\qquad)$。
    (A)$\mu_0 I$
    (B)$-\mu_0 I$
    (c)$\mu_0 I \sin \theta $
    (D)$\mu_0 I \cos \theta$
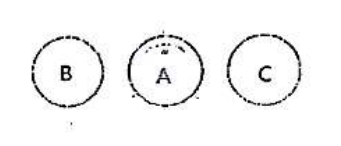
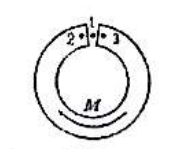
    (E)$\mu_0 I \tan \theta$
    
    图 6
32. 一金属圆环 $A$ 带负电荷，绕着轴线顺时针转动，另外两个金属园环 B 和 C 与 A 在同一平面内。当 A 的转速越来越快时，B 和 C 中的感应电流方向是 $(\qquad)$
    (A)电流 B 顺时针,电流 C 顺时针 (B)电流 B 逆时针，电流 C 顺时针 (C)电流 B 顺时针，电流 C 逆时针 (D)电流 B 逆时针，电流 C 逆时针 (E)B 和 C 中无电流
    
    图 7
33. 在如图所示的霍尔元件中，载流子带正电。如果元件的下表面处于高电势。则磁感应强皮矢量 B 的方向为 $(\qquad)$。
    (A)向上
    (B)向下
    (C)向纸外
    (D)向纸内
    (E)向左
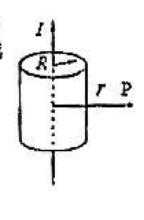
    (F)向右
    
    图 8
34. 一圆柱形的长直导线，截面半径为 R，稳恒电流均匀通过导线的截面，电流为 $I$，P 点到圆柱轴线的垂直距离为 r，如图所示设导线内的磁感应强度为 $B_\text{内}$，导线外的磁感应强度为 $B_\text{外}$，则有 $(\qquad)$。
    (A)$B_\text{内},B_\text{外}$ 都与 r 成正比
    (B)$B_\text{内},B_\text{外}$ 都与 r 成反比
    (C)$B_\text{内}$ 与 r 成反比，$B_\text{外}$ 与 r 成正比
    (D)$B_\text{内}$ 与 r 成正比，$B_\text{外}$ 与 r 成反比
    
    图 9
35. 一个空心螺环绕的自感为 $L_0$,加入铁芯后自感为 $L_1$,在铁芯上锯开一个很窄的断口后自感为 $L_2$,$L_0,L_1,L_2$ 三者的大小关系为 $(\qquad)$。
    (A)$L_0< L_1< L_2$
    (B)$L_0< L_2< L_1$
    (C)$L_1< L_2< L_0$
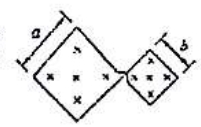
    (D)$L_2< L_1< L_0$
36. 如图所示，一平面线圈由两个用导线折成的正方形线圈联结而成.一均匀磁场垂直于线网平面，其磁感强度按 $B=B_0\sin \omega t$ 的规律变化，则线圈中感应电动势的最大值是 $(\qquad)$。
    
    图 10
37. 载流导线形状如图所示，O 处的磁感应强 D 的大小为 $(\qquad)$。
    
    图 11
38. 如图所示，是一个带有很窄缝隙的永磁环，磁化强度为 M，则图中所标各点场强度为 $H_1=(\quad);H_2=(\quad);H_3=(\quad);$
    
    图 12
39. 一平行板空气电容器的两极板都是半径为 r 的圆形导电片，在充电时， 板间电场强度的变化率为 $\displaystyle \frac{dE}{dt}$,若略去边缘效应，则两板问的位移电流为 $(\qquad)$。
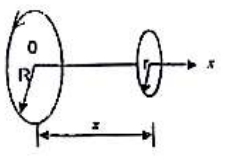
40. 半径为 R，电流为 I 的大圆环，在其中央轴线上距环心 X 处的磁感应强度 $B(x)=(\quad)$。有一半径 r<<R 的小圆环，环心位于 X 点，环面与 X 轴垂直，如图所示，则小圆环与大圆环之间的互感系数近似为 $\mu=(\quad)$。
    
    图 13
41. 在光电效应的实验中，单个电子的最大发射动能取决于入射光的 $(\qquad)$
    (A)强度
    (B)波长
    (C)偏振方向
    (D)照射时间
42. 太阳风到达地球时，会让高层大气分子、原子激发或电离，产生美丽的极光。极光中的红色成可能来自氢原子光谐的 $(\qquad)$
    (A)菜曼系
    (B)巴耳末系
    (C)帕邢系
    (D)布拉开系
43. 定量计算碱金属双线时，不需愿考虑 $(\qquad)$
    (A)电子自旋
    (B)电子磁矩
    (C)两个电子的耦合
    (D)相对论效应
44. 原子的某个支壳层中有 14 个电子，则该支壳可能同子下列哪个主壳层？
    (A)K 壳层
    (B)L 壳层
    (C)M 壳展
    (D)N 壳层
45. 弱磁场中原于谱线一分为三，相邻谱线的能量间隔都是 $2\mu_B B$，这属于 $(\qquad)$
    (A)正常塞曼效应
    (B)反常赛曼效应
    (C)线性斯路克效应
    (D)非线性斯塔克效应
46. 已知普朗克常数 $h=6.63$x$10^{-34}J.s$，光速 $c=3.00$x$10^8 m/s$。某带电粒子的康普顿波长是 $1.2$x$10^{-14}m$，速度是 $2.0$x$10^6 m/s$，则该粒子的德布罗意波长为 $(\qquad)$m。
47. 根据玻尔模型，氢原子的电子跃迁时，若轨道角动量变成原来的 3 倍，则能量变成原来的 $(\qquad)$ 倍。
48. 根据量子力学，氢原子中电子的轨道量子数 $l=2$ 时，它的轨道动量大小 L=$(\qquad)$h。
49. 2014 度诺贝尔物理学奖授予日本名古屋大学的赤崎勇、天野浩以及美国加州大学圣巴巴拉分校的中村修二。他们经过数千次实验，用氮化镓晶体研制出蓝色发光二极管(LED)。镓是 LED 的常用元素，它的基态电于组态是 $3d^{10}4s^24p$，原子态符号是 $(\qquad)$。
50. $J_1=J_2=\frac{3}{2}$ 的两个同科电子发生 J-J 耦合，则合成的总角动量量子数 J 的可能取值为 $(\qquad)$。