华东师范大学 2014 年考研物理考试试题

贡献者：待更新

　　声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

　　普适气体常量 $R=8.31J(mol.K)$

　　波尔拉曼常 $k=1.38*10^{-22} J/K$

　　电子质量 $m_t=9.11*10^{-38}kg$

　　真空介电常量 $\varepsilon_0=8.85*10^{-12}C^2.N^{-3}.m^{-2}$

　　普朗克常量 $h=6.63*10^{-36}J.s$

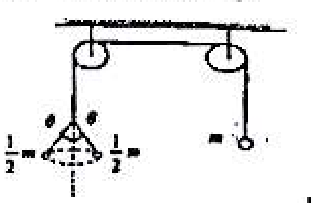
绳子通过两个定滑轮，右端挂质量为 m 的小球，左端挂有两个质量 $m_1=m/2$ 的小球,将右边小球约束，使之不动。使左边两小球绕竖直轴对称匀速地旋转，如图所示，则去掉约束时，右边的小球将：$(\quad)$
(A)向上运动
(B)向下运动
(C)保持不动
(D)饶滑轮摆动

图 1
一炮弹由于特殊原因在水平飞行过程中，突然炸裂成两块,其中一块作自由下落，则另一块着地点(飞行过程中阻力不计)$(\quad)$
(A)比原来更远
(B)比原来更近
(C)仍和原来一样远
(D)条件不足，不能判定
质量为 $m$ 的小孩站在半径为 $R$ 的水平平台边缘上，平台可以绕通过其中心的竖立光滑固定轴自由转动，转动惯量为 $J$。平台和小孩开始时均静止。当小孩突然以相对于地面为 $v$ 的速率在台边缘沿逆时针转向走动时，则此平台相对地面旋转的角速度和旋转方向分别为 $(\quad)$
(A) $\omega=\frac{mR^2}{J}(\frac{v}{R})$,顺时针 (B) $\omega=\frac{mR^2}{J}(\frac{v}{R})$,逆时针 (C) $\omega=\frac{mR^2}{J+mR^2}(\frac{v}{R})$,顺时针 (D) $\omega=\frac{mR^2}{J+mR^2}(\frac{v}{R})$,逆时针
将细绳绕在一个具有水平光滑轴的飞轮边缘上，现在在绳端挂一质量为 $m$ 的重物，飞轮的角加速为 a，如果以拉力 $2mg$ 代替重物拉绳时，飞轮的角加速度将 $(\quad)$
(A)小于 a
(B)大小 a,小于 2a
(C)大于 2a
(D)等于 2a
一电子的总能量为 $5.0MeV$，则该电子的运动速率、动能和动量分别为(电子的静质量为 $9.1*10^8kg,leV=1.6*10^{-10}J,c=3*10^8$ 代表光速)
(A)$0.995c,4.488 MeV,2.66*10^{41}kg.m.s^{-1}$ (B)$0.995c,0.512 MeV,2.66*10^{41}kg.m.s^{-1}$ (C)$0.995c,8.96*10^{-15},2.66*10^{32}kg.m.s^{-1}$ (D)$0.995c,8.96*10^{-15},2.72*10^{28}kg.m.s^{-1}$
在宇宙飞船上的人从飞船后面向前面的靶子发射一颗高速子弹，此人测得离靶子的距离为 60m，子弹的速度 0.8c，求当飞船对地球以 0.6c 的速度运动时，地球上的观察者测得子弹飞行的时间分别为 $(\quad)$
(A)$25$X$10^{-7}$s
(B)$2$X$10^{-7}$s
(C)$3.125$X$10^{-7}$s
(D)$4.63$X$10^{-5}$
一个质量为 $m$ 的质点，仅受到力 $\vec F=k\vec r/r^3$ 的作用，式中 K 为常量，$\vec r$ 为从某一定点到质点的矢径，该质点在 $r=r_B$ 处被释放，由静止开始运动，当它到达无穷远时的速率为:$(\quad)$
(A)$\displaystyle v=\frac{2k}{mr_0}$
(B)$\displaystyle v=\sqrt{\frac{2k}{mr_0}}$
(C) $\displaystyle v=\frac{k}{mr_0}$
(D)$\displaystyle v=\frac{2k}{m}\ln r_0$
一长为 l，质量均匀的链条，放在光滑的水平桌面上，若使其长度的一半悬于桌边下，然后由静止释放，任其滑动，则它全部离开桌面时的速率为:$(\quad)$
(A)$\frac{1}{2}\sqrt{3gl}$
(B)$\sqrt{\frac{3}{2}gl}$
(C)$\sqrt{\frac{3}{2}}gl$
(D)$\frac{\sqrt{3}}{2}$
用一根细线吊一重物，重物质量为 $5kg$，重物下面再系一根同样的细线，细线只能经受 $70N$ 的拉力,现在突然向下拉一下下面的线。设力最大值为 50N，则 $(\quad)$
(A)下面的线先断
(C)两根线一起断
(B)上面的线先断
(D)两根线都不断
轮船在水上以相对于水的速度 $\vec v_1$ 航行，水流速度为 $\vec v_2$，一人相对于甲以速度 $\vec v_3$ 行走，如人相对于岸静止，则 $\vec v_1,\vec v_2,\vec v_3$ 的关系是 $(\quad)$
(A)$\vec v_1+\vec v_2=\vec v_3$
(B)$\vec v_1+\vec v_3=\vec v_2$
(C)$\vec v_2+\vec v_3=\vec v_1$
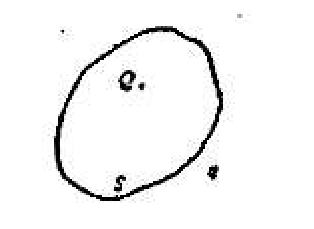
(D)$\vec v_1+\vec v_2+\vec v_3=0$
点电荷 $Q$ 被曲面 $S$ 所包，从无穷远处引入另一点电荷 $q$ 至曲面外一点，如图所示，则引入前后:$(\quad)$
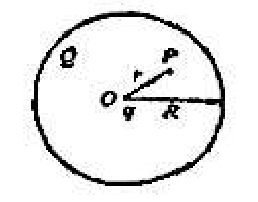
(A)通过曲面 S 的电通量不变，曲面上各点场强不变 (B)通过曲面 S 的电通量变化，曲面上各点场强不变 (C)通过曲面 S 的电通量变化，曲面上各点场强变化 (D)通过曲面 S 的电通量不变，曲面上各点场强变化

图 2
真空中一半径为 $R$ 的球面均匀带电 $Q$,在球心 O 处有一带电量为 $q$ 的点电荷如图所示，设无穷远处为电势零点，则在球内离球心 O 距离为 $r$ 的 $P$ 点处的电势为 $(\quad)$
(A) $\displaystyle \frac{q}{4\pi \varepsilon_0 r}$
(B) $\displaystyle \frac{1}{4\pi \varepsilon_0}(\frac{q}{r}+\frac{Q}{R})$
(C) $\displaystyle \frac{q+Q}{4\pi \varepsilon_0 r}$
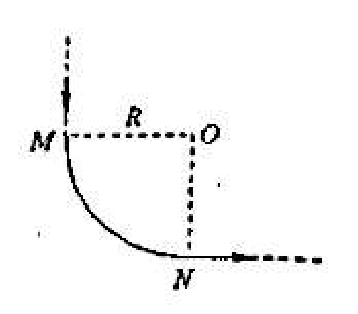
(D) $\displaystyle\frac{1}{4\pi \varepsilon_0}(\frac{q}{r}+\frac{Q-q}{R})$

图 3
一无限长载流导线，在中部弯成如图所示的四分之一圆周 MN，圆心为 O，半径为 R，则在 O 点处的磁感应强度 B 的大小为 $(\quad)$
(A)$\displaystyle \frac{\mu_0 I}{2\pi R} $
(B)$\displaystyle \frac{\mu_0 I}{2\pi R}(I+\frac{\pi}{4})$
(C)$\displaystyle \frac{\mu_0 I}{8 \pi R}$
(D)$\displaystyle \frac{\mu_0 I}{8R}$

图 4
一个介质球壳相对介电常数为 $\varepsilon_r$。，其内半径为 R。外半径为 $R+a$，在球心有一电量为 $q_0$ 的点电荷，对于 $R< r< R+a$ 电场强度为 $(\quad)$
(A) $\displaystyle \frac{q_0}{4\pi \varepsilon_0 \varepsilon_r r^2}$
(B)$\displaystyle \frac{q_0}{4\pi \varepsilon_0 r^2}$
(C)$\displaystyle \frac{q_0}{4\pi \varepsilon_r r^2}$
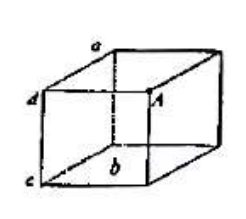
(D)$\displaystyle \frac{(\varepsilon_r-1)q_0}{4\pi \varepsilon_r r^2}$
如图所示，一点电荷 $q$ 位于立方体 $A$ 角上，则通过侧面 $abcd$ 的电通量为 $(\quad)$
(A) $\displaystyle \frac{1}{4} \frac{q}{\varepsilon_0}$
(B) $\displaystyle \frac{1}{6} \frac{q}{\varepsilon_0}$
(C) $\displaystyle \frac{1}{6} \frac{q}{\varepsilon_0}$
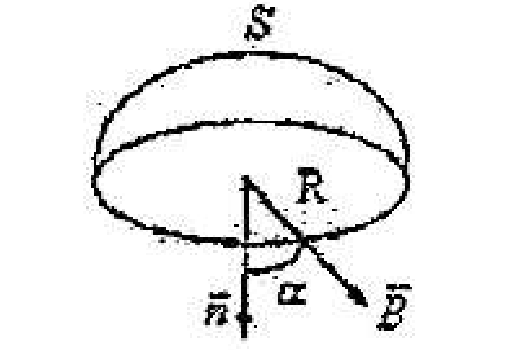
(C) $\displaystyle \frac{1}{24} \frac{q}{\varepsilon_0}$

图 5
如图所示，在磁感应强度为 $\vec B$ 的均匀磁场中作一半径为 $R$ 的半球面 $S$,$S$ 边线所在平面的法线方向单位矢量 $\vec n$ 与 $\vec B$ 的夹角为 $\alpha$，则通过半球面 $S$ 的磁通量为 $(\quad)$
(A) $\pi R^2 B$
(B)$2pi R^2 B$
(C)$\pi R^2 B \sin \alpha$
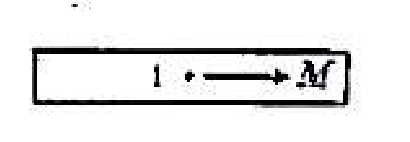
(D)$\pi R^2 B \sin \alpha$

图 6
下图是一根沿轴向均勾磁化的细长水久磁棒，磁化强度为 $M$,图中标出的 $I$ 点的 $B$ 值是 $(\quad)$
(A)$\mu_0 M$
(B)0
(C)$\displaystyle \frac{1}{2} \mu_0 M$
(D)$\displaystyle -\frac{1}{2} \mu_0 M$

图 7
平行板电容器充电后与电源断开。然后充满相对介电常数为 $\varepsilon_0$ 的均匀介质。则电场强度 $E$、电容 $C$ 电压 $U$、电场能量 $W$ 护四个量和充介质前相比较是 $(\quad)$
(A)$E \uparrow ,C\uparrow ,U\uparrow ,W\uparrow$
(B)$E \downarrow ,C\uparrow ,U\downarrow ,W\uparrow$
(C)$E \downarrow ,C\uparrow ,U\uparrow ,W\downarrow$
(D)$E \uparrow ,C\uparrow ,U\downarrow ,W\downarrow$
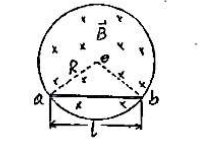
在一半径为 $R$ 的均匀圆柱体内充满磁感应强度为后的均匀磁场，这磁场以速率 $\frac{dB}{dt}$ 在减小,如图放置的金属棒 $ab(ab=1<2R)$ 两端的感生电动势 $\varepsilon_{ab}$ 为 $(\quad)$
(A) $\displaystyle l \sqrt{R^2-(\frac{l}{2})^2} \frac{\mathrm{d}{B}}{\mathrm{d}{t}} $,a 点电势高
(B) $\displaystyle \frac{l}{2}l \sqrt{R^2-(\frac{l}{2})^2} \frac{\mathrm{d}{B}}{\mathrm{d}{t}} $,a 点电势高
(C) $\displaystyle \frac{l}{2}l \sqrt{R^2-(\frac{l}{2})^2} \frac{\mathrm{d}{B}}{\mathrm{d}{t}} $,b 点电势高
(D) $\displaystyle l \sqrt{R^2-(\frac{l}{2})^2} \frac{\mathrm{d}{B}}{\mathrm{d}{t}} $,b 点电势高

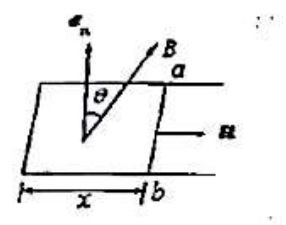
图 8
均匀磁场与导体回路法线 $e_a$ 的夹角为 $\theta=\pi/3$，磁感强度 $B$ 随时间按正比的规律增加，即 $B=kt(k>0)$，$ab$ 边长为 $l$，且以速度 $u$ 向右滑动(设 $t=0$ 时，$x=0$)，则导体回路内任意时刻感应电动势的大小和方向为:$(\quad)$
(A)$\displaystyle 2kult$ 逆时针方向
(B)$\displaystyle \frac{1}{2kult}$ 顺时针方向
(C)$kult$ 顺时针方向
(D)$kult$ 逆时针方向

图 9
光场中某一点的复振幅为 $-Ae^\theta/(2i)$，则该点电场震动的相位为:$(\quad)$
(A) $\theta$
(B) $\theta-\pi/2$
(C) $\theta+\pi/2$
(D)0
在杨氏双缝于涉实验中，将实验装置从空气中移到水中，则观测屏上:$(\quad)$
(A)条纹间距变大
(B)条纹间不变
(C)条纹间距变小
(D)条纹消失
用单色光垂直照射在牛顿环装置上，将其平凸透镜直地向上平移，可以观察到于涉条纹：$(\quad)$
(A)向右平移
(B)向中心收缩
(C)向外扩张
(D)静止不动向左平移
(E)向左平移
菲涅尔圆孔衍射中，对圆孔轴上某一参考点，衍射孔仅包含 $ 1/2$ 个半波带，现在撤掉衍射屏，点光强变为原来的 $(\quad)$
(A)1/2
(B)2 倍
(C)1/4
(D)4 倍
(E)1 倍
在单缝夫琅禾费衍射实验中，单色平行光沿水平方向垂直射向单缝，现将单缝向上平移一小段距离，则观测屏上的条纹 $(\quad)$
(A)向上平移
(B)向下平移
(C)不动
(D)间距变大
在光栅夫琅禾费衍射实验中，单色平行光由垂直射向光栅改为斜入射光栅，观察到的光谱线 $(\quad)$
(A)最高级次变小，条数不变
(B)最高级次变大,条数不变
(C)最高级次变大，条数变多
(D)最高级次不变，条数不变
光栅的总缝数为 $N$，光栅常数为 $d$，则对某一级光谱而言，其分辨本领 $(\quad)$
(A)由 N 决定
(B)由 d 决定
(C)由 Nd 决定
(D)由 1/(Nd)决定
右旋园偏振光垂直通过 1/2 波片后，其出射光的偏振态是 $(\quad)$
(A)左旋圆偏振光
(B)右旋圆振光
(C)左旋椭圆偏振光
(D)右旋椭圆偏振光
三个偏振片 $P1,P2$ 与 $P3$ 堆叠在一起，$P1$ 与 $P3$ 的偏振化方向相互垂直，$P2$ 与 $P1$ 的偏振化方向夹角为 30°，强度为 $I$ 的自然光垂直入射到偏振片 $P1$，并依次透过振片 $P1,P2$ 与 $P3$，若不考虑偏振片的吸收和反射，则通过三个偏振片后的光强为 $(\quad)$
(A)I/4
(B)3I/8
(C)3I/16
(D)3I/32
一黑体为立方体空腔，现将空腔的边长增大一倍，而空腔及腔壁的温度降低一半，则黑体辐射的能量与原有的辐射能量之比为 $(\quad)$
(A) 4:1
(B) 1:4
(C) 1:1
(D) 1:2
(E) 2:1
绝对黑体具有的重要特点是 $(\quad)$
(A)不吸收电磁波
(B)不反射电磁波
(C)不辐射电磁波
(D)不辐射可见光
已知普朗克常数 $h=6.63$x$10^{-34}J.s$，光速 $c=3.00$x$10^8m.s^{-1}$。某带电粒子的质量是 $1.84$x$10-{-28}kg$,速度是 $2.0$x$10^4 m/s$，则该粒子的康普顿波长为 $(\quad)$
(A)$1.8$x1$0^{-12}$
(B)$1.2$x$10^{-14}$
(C)$1.8$x$10^{-18}$
(D)$4.0$x$10^{-23}$
根据玻尔理论可以计算氢原子光谱的 $(\quad)$
(A)强度
(B)宽度
(C)频率
(D)俯振
当氢原子中从第一激发态跃迁到基态时，核外电子的运动速度变成原来的 $(\quad)$
(A)1/2
(B)1/4
(C)2 倍
(D)4 倍
2012 年，欧洲核子研究中心发现了静止质量为 $m=2.24$x$10^{-25}kg$ 的希格斯粒子。理论预言，这种希格斯粒子的质量不确定度为 $\Delta m/m$=$1.67$x$10^{-5}$。已知普朗克常数 $h=6.63$x$10^{-34}J.s$，光速 $c=3.00$x$10^8 m/s$。根据不确定性关系可估算，该粒子的平均寿命的理论值最接近 $(\quad)$
(A)$10^{-5}$
(B)$10^{-10}$
(C)$10^{-22}$
(D)$10^{-29}$
下列实验现象，不需要引入电子自旋的概念就能解释的是 $(\quad)$
(A)碱金属双线
(B)施特恩-格拉赫实验
(C)正常塞曼效应
(D)反常塞曼效应
下列原子态符号中，错误的是 $(\quad)$
(A)$^1S_1$
(B)$^1S_{u2}$
(C)$^1p_1$
根据电偶极辐射跃迁的选择规则，电子组态 $1S^2$ 可以跃迁到 $(\quad)$
(A)2s2s
(B)2s2p
(C)2$p^2$
(D)3s3d
原子系统处于正常状态时，每个电子趋向占据 $(\quad)$ 的态。 (A)主量子数最小
(B)角量子数最小
(C)自旋量子数最小
(D)能量最低
根据泡利原理，在 $I=2$ 的次壳层中，最多可以容纳的电子数为 $(\quad)$
(A)4
(B)8
(C)5
(D)10
一定量的理想气体储存于某一容器中，温度为 T，气体分子的质量为，则分子速度在 X 方向分量的平均值为 $(\quad)$
(A)$\displaystyle \bar {v_x}=\sqrt{\frac{8kT}{\pi m}}$
(B)$\displaystyle \bar {v_x}=\frac{1}{3}\sqrt{\frac{8kT}{\pi m}}$
(C)$\displaystyle \bar {v_x}=\sqrt{\frac{8kT}{3\pi m}}$
(D)$\displaystyle \bar {v_x}=0$
在一封闭容器中盛有 $1mol$ 氮气(可视为理想气体)，这时分子无规则运动的平均自由程仅取决于 $(\quad)$
(A)压强 P
(B)体积 V
(C)温度 T
(D)平均碰撞频率
物质量相同的氦气和氮气(可视为理想气体)，从相的初状态(P，V，T 相同)开始做等膨胀到同一末状态，则下列说法正确的是 $(\quad)$
(A)对外所做的功相同
(B)从外界吸收的热量相同
(C)气体分子平均速率的增量相同
(D)以上说法都不正确
一定量的真实气体，绝热地向真空自由膨胀，则气体 $(\quad)$
(A)温度上升
(B)温度下降
(C)温度不变
摩尔数相同的氢气和氨气，若它们的温度相同，则两气体 $(\quad)$
(A)内能必相等
(B)分子的平均动能相同
(C)分子的平均平动能相同
(D)分子的平均速率相同
$1mol$ 的理想气体由最初温度 $T_1$ 绝热地影胀到最终温度 $T_2$，则气体对外所做的功为 $(\quad)$
(A)$R(T_1-T_2)$
(B)$C_v(T_1-T_2)$
(C)$C_v \ln\left(T_1-T_2\right) $
(D)$C_p(T_1-T_2)$
若在一个固定的容器内，理想气体分子的平均速率提高为原来的 2 倍，则有 $(\quad)$
(A)温度为原来的 2 倍，压强为原来的 4 倍
(B)温度和压强都为原来 2 倍
(C)温度为原来的 4 倍，压强为原来的 2 倍
(D)温度和压强都为原来 4 倍
若在某个过程中，一定量的理想气体的内能 $E$ 随压强的变化关系为一直线，则该过程为 $(\quad)$
(A)等温过程
(B)等压过程
(C)等体过程
(D)绝热过程
一个体积为 v 的容器，充入温度为 $T_1$ 的双原子分子的理想气体，强为 P，当器内的气体被加热，温度开高到 $T_2$ 之后，因容器漏气而压强仍为 P，则容器内气体的内能 $(\quad)$
(A)变大
(B)变小
(C)不变
(D)无法确定
一定量的理想气休，起始温度为 T，体积为 v，经绝热过程后体积变为 2V，又经过等压过程后温度回升到起始温度，最后经过等温过程回到起始状态，在此循环过程中 $(\quad)$
(A)气体从外界净吸热为负值
(B)气体对外界净做功为正值
(C)气体从外界净吸热为正值
(D)气体内能减少

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。