格林公式（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 在向量分析中，格林公式把围绕一条简单闭合曲线 $C$ 的曲线积分与该曲线所围平面区域 $D$（即 $\mathbb{R}^2$ 中的曲面）的二重积分联系起来。它是斯托克斯定理在二维空间（$\mathbb{R}^2$）中的特例。在一维情形下，它等价于微积分基本定理；在三维情形下，它则等价于散度定理。

1. 定理

　　 设 $C$ 是平面上一条按正向（逆时针）取向、分段光滑的简单闭合曲线，$D$ 是 $C$ 所围成的区域。如果 $L$ 和 $M$ 是定义在包含 $D$ 的某个开区域上的函数，且它们在该区域内具有连续偏导数，则有 $$ \oint_{C} (L\,dx + M\,dy) = \iint_{D} \left( \frac{\partial M}{\partial x} - \frac{\partial L}{\partial y} \right) dA~ $$ 其中，曲线 $C$ 上的积分路径方向为逆时针。

2. 应用

　　 在物理学中，格林公式有许多应用。例如，在处理二维流体积分问题时，可以用它说明：一个区域内流体的总外流量等于该区域边界曲线上的总外流量。在平面几何中，尤其是在面积测量中，格林公式还能用于仅通过对边界积分来求解平面图形的面积和形心位置。

3. 当 $D$ 是单连通区域时的证明

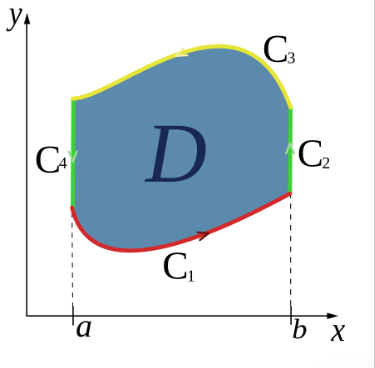
　　 以下是对简化区域 $D$ 的一半定理的证明。这里 $D$ 是 I 型区域，其边界曲线 $C_1$ 和 $C_3$ 由垂直线段（长度可能为零）连接。对于 II 型区域（边界曲线 $C_2$ 和 $C_4$ 由水平线段连接）的另一半定理，也存在类似的证明。将这两部分结合起来，就可以证明适用于 III 型区域（既是 I 型又是 II 型区域）的格林公式。通过将一般区域 $D$ 分解为一组 III 型区域，还可以将结论推广到更一般的情形。

　　 如果能够证明以下两式： $$ \oint_{C} L\,dx = \iint_{D} \left( -\frac{\partial L}{\partial y} \right) dA \tag{1}~ $$ 以及 $$ \oint_{C} M\,dy = \iint_{D} \left( \frac{\partial M}{\partial x} \right) dA \tag{2}~ $$ 那么对于区域 $D$ 格林公式就立即成立。对于 I 型区域，式 (1) 容易证明；对于 II 型区域，式 (2) 也可以类似地证明。由此，格林公式便适用于 III 型区域。

　　 假设区域 $D$ 是 I 型区域，因此它可以表示为（如上图所示）： $$ D = \{(x, y) \mid a \leq x \leq b, \; g_1(x) \leq y \leq g_2(x)\},~ $$ 其中 $g_1$ 和 $g_2$ 是区间 $[a, b]$ 上的连续函数。计算式 (1) 中的二重积分： $$ \begin{aligned} \iint_D \frac{\partial L}{\partial y} \, dA &= \int_a^b \int_{g_1(x)}^{g_2(x)} \frac{\partial L}{\partial y}(x, y) \, dy \, dx \\ &= \int_a^b \big[ L(x, g_2(x)) - L(x, g_1(x)) \big] \, dx. \end{aligned} \tag{3}~ $$ 计算式 (1) 中的曲线积分：曲线 $C$ 可以分解为四段：$C_1, C_2, C_3, C_4$。 沿 $C_1$，参数方程为：$x = x,\; y = g_1(x),\; a \leq x \leq b$.因此： $$ \int_{C_1} L(x, y) \, dx = \int_a^b L(x, g_1(x)) \, dx~ $$ 沿 $C_3$，参数方程为：$x = x,\; y = g_2(x),\; a \leq x \leq b$.因为方向相反，积分为： $$ \int_{C_3} L(x, y) \, dx = \int_b^a L(x, y) \, dx = -\int_a^b L(x, g_2(x)) \, dx~ $$ 在 $C_3$ 上积分需要取负号，是因为曲线从 $b$ 到 $a$ 的方向与正向（逆时针方向）相反。 在 $C_2$ 和 $C_4$ 上，$x$ 保持不变，因此： $$ \int_{C_4} L(x, y)\, dx = \int_{C_2} L(x, y)\, dx = 0~ $$ 因此： $$ \begin{aligned} \oint_{C} L\, dx &= \int_{C_1} L(x, y)\, dx + \int_{C_2} L(x, y)\, dx + \int_{C_3} L(x, y)\, dx + \int_{C_4} L(x, y)\, dx \\ &= \int_a^b L(x, g_1(x))\, dx - \int_a^b L(x, g_2(x))\, dx \end{aligned} \tag{4}~ $$ 将式 (3) 与式 (4) 结合，就得到了适用于 I 型区域的式 (1)。用相同的思路处理相应端点，可以得到适用于 II 型区域的式 (2)。将这两部分结合，就得到了适用于 III 型区域的最终结果。

4. 可整曲线的证明

　　 我们要证明如下结论：

　　 定理 —— 设 $\Gamma$ 是 $\mathbb{R}^2$ 中一条可整、按正向取向的 Jordan 曲线，并设 $R$ 是其内部区域。假设函数 $A, B : \overline{R} \to \mathbb{R}$ 在闭区域 $\overline{R}$ 上连续，且满足：$A$ 在区域 $R$ 内的每一点都有二阶偏导数；$B$ 在区域 $R$ 内的每一点都有一阶偏导数；函数 $ D_1 B, \; D_2 A : R \to \mathbb{R}$ 在 $R$ 上是黎曼可积的。

　　 则有： $$ \int_{\Gamma} \big( A\,dx + B\,dy \big) = \int_{R} \big( D_1 B(x, y) - D_2 A(x, y) \big) \, d(x, y)~ $$

　　 我们需要以下引理，其证明可参见文献 [3]：

　　 引理 1（分解引理） —— 假设 $\Gamma$ 是平面上一条可整、按正向取向的 Jordan 曲线，并设 $R$ 为其内部区域。对于任意正实数 $\delta$，令 $\mathcal{F}(\delta)$ 表示平面上由直线 $x = m\delta,\; y = m\delta$ （其中 $m$ 为整数）所围成的正方形的集合。那么，对于该 $\delta$，可以将闭区域 $\overline{R}$ 分解为有限个互不重叠的子区域，使得：

1. 每一个完全包含在 $R$ 内的子区域（记为 $R_1, R_2, \ldots, R_k$）都是 $\mathcal{F}(\delta)$ 中的某个正方形。
2. 其余的子区域（记为 $R_{k+1}, \ldots, R_s$）的边界由有限条 $\Gamma$ 的弧段和 $\mathcal{F}(\delta)$ 中某些正方形的边组成，构成一条可整的 Jordan 曲线。
3. 每个边界子区域 $R_{k+1}, \ldots, R_s$ 都可以被一个边长为 $2\delta$ 的正方形所覆盖。
4. 如果 $\Gamma_i$ 是子区域 $R_i$ 的按正向取向的边界曲线，则有：$\Gamma = \Gamma_1 + \Gamma_2 + \cdots + \Gamma_s$。
5. 这些边界子区域的数量 $s-k$ 不超过：$4\left(\frac{\Lambda}{\delta} + 1\right)$，其中 $\Lambda$ 表示曲线 $\Gamma$ 的总长度。

　　 引理 2 —— 设 $\Gamma$ 是平面上的一条可整曲线，定义 $\Delta_{\Gamma}(h)$ 为平面上到曲线 $\Gamma$ 的轨迹距离不超过 $h$ 的点集。那么该集合的外 Jordan 测度满足：$\overline{c}\,\Delta_{\Gamma}(h) \leq 2h\Lambda + \pi h^2$，其中 $\Lambda$ 表示曲线 $\Gamma$ 的长度。

　　 引理 3 —— 设 $\Gamma$ 是 $\mathbb{R}^2$ 中一条闭合的可整曲线，且 $f : \text{range of } \Gamma \to \mathbb{R}$ 是定义在 $\Gamma$ 上的连续函数。那么： $$ \left| \int_{\Gamma} f(x, y)\, dy \right| \leq \frac{1}{2} \Lambda \, \Omega_f,~ $$ 以及 $$ \left| \int_{\Gamma} f(x, y)\, dx \right| \leq \frac{1}{2} \Lambda \, \Omega_f,~ $$ 其中，$\Omega_f$ 表示函数 $f$ 在曲线 $\Gamma$ 上的振幅（最大值与最小值之差）。 现在我们可以开始证明这个定理了：

　　 定理的证明。设 $\varepsilon$ 是任意给定的正实数。由于 $A$、$B$ 在 $\overline{R}$ 上连续，且 $\overline{R}$ 是紧集，所以给定 $\varepsilon > 0$，存在 $0 < \delta < 1$，使得只要 $\overline{R}$ 中任意两点的距离小于 $2\sqrt{2}\,\delta$，它们在 $A,B$ 作用下的函数值之差就小于 $\varepsilon$。

　　 在这个 $\delta$ 下，考虑前一条引理给出的分解。我们有 $$ \int_{\Gamma} A\,dx + B\,dy = \sum_{i=1}^{k} \int_{\Gamma_i} A\,dx + B\,dy + \sum_{i=k+1}^{s} \int_{\Gamma_i} A\,dx + B\,dy.~ $$ 令 $\varphi := D_1 B - D_2 A$。

　　 对于每个 $i \in \{1, \ldots, k\}$，曲线 $\Gamma_i$ 是一条按正向取向的正方形边界，因此格林公式在该区域成立。于是有： $$ \sum_{i=1}^{k} \int_{\Gamma_i} A\,dx + B\,dy = \sum_{i=1}^{k} \int_{R_i} \varphi = \int_{\bigcup_{i=1}^{k} R_i} \varphi.~ $$ 边界区域中的每个点与曲线 $\Gamma$ 的距离都不超过 $2\sqrt{2}\,\delta$。因此，如果用 $K$ 表示所有边界区域的并集，那么有：$K \subset \Delta_{\Gamma}(2\sqrt{2}\,\delta)$，根据引理 2，可得：$c(K) \leq \overline{c}\,\Delta_{\Gamma}(2\sqrt{2}\,\delta)\leq 4\sqrt{2}\,\delta + 8\pi\delta^2$. 注意： $$ \int_{R} \varphi - \int_{\bigcup_{i=1}^{k} R_i} \varphi = \int_{K} \varphi.~ $$ 由此得到： $$ \left| \sum_{i=1}^{k} \int_{\Gamma_i} A\,dx + B\,dy - \int_{R} \varphi \right| \leq M\delta \bigl(1 + \pi\sqrt{2}\,\delta \bigr),~ $$ 其中 $M > 0$。

　　 我们可以进一步选择 $\delta$，使得上述不等式右边小于 $\varepsilon$。

　　 在本证明开头的推论表明，函数 $A$ 和 $B$ 在每个边界区域上的振幅都不超过 $\varepsilon$。因此有： $$ \left| \sum_{i=k+1}^{s} \int_{\Gamma_i} A\,dx + B\,dy \right| \leq \frac{1}{2}\,\varepsilon \sum_{i=k+1}^{s} \Lambda_i .~ $$ 根据引理 1(iii) 可得： $$ \sum_{i=k+1}^{s} \Lambda_i \leq \Lambda + (4\delta)\,4\!\left(\frac{\Lambda}{\delta} + 1\right) \leq 17\Lambda + 16.~ $$ 结合以上不等式，最终得到： $$ \left| \int_{\Gamma} A\,dx + B\,dy - \int_{R} \varphi \right| < C\,\varepsilon ,~ $$ 其中 $C > 0$。

　　 由于这一结果对任意 $\varepsilon > 0$ 都成立，证明完毕。

5. 在不同假设下的适用性

　　 前述定理中的假设并不是格林公式成立的唯一条件。另一组常见的条件如下：

　　 函数 $A, B : \overline{R} \to \mathbb{R}$ 依然假设是连续的，但现在要求它们在区域 $R$ 的每个点都是 Fréchet 可微的。这意味着所有方向导数都存在，特别是：$D_{e_i} A := D_i A, \quad D_{e_i} B := D_i B, \quad i = 1, 2$,其中，$(e_1, e_2)$ 是 $\mathbb{R}^2$ 的标准有序基。此外，还要求函数：$D_1 B - D_2 A$ 在区域 $R$ 上是 Riemann 可积的。

　　 由此可以得到关于可测度 Jordan 曲线的柯西积分定理：

　　 定理（柯西）——如果 $\Gamma$ 是复平面 $\mathbb{C}$ 中的一条可测度 Jordan 曲线，并且 $f : \overline{\text{内区域}(\Gamma)} \to \mathbb{C}$ 是在 $\Gamma$ 的闭合内区域上连续、并且在该区域内部处处全纯的映射，则有： $$ \int_{\Gamma} f = 0,~ $$ 其中该积分为复平面中的复路径积分。

　　 证明

　　 我们将复平面视为 $\mathbb{R}^2$。定义函数 $u, v : \overline{R} \to \mathbb{R}$ 使得：$f(x + iy) = u(x, y) + i v(x, y)$.显然，$u$ 和 $v$ 都是连续的。众所周知，$u$ 和 $v$ 在区域内都是 Fréchet 可微的，并且满足柯西–黎曼方程：$D_1 v + D_2 u = 0, \quad D_1 u - D_2 v = 0$.接下来，分析定义复路径积分的求和式，可以很容易看出： $$ \int_{\Gamma} f = \int_{\Gamma} u \, dx - v \, dy + i \int_{\Gamma} v \, dx + u \, dy,~ $$ 其中右边的积分都是普通的线积分。由于这些积分分别满足应用格林公式的条件，因此将格林定理应用于每一部分后，可以得到：$\int_{\Gamma} f = 0$.

6. 多连通区域

　　 定理

　　 设 $\Gamma_0, \Gamma_1, \ldots, \Gamma_n$ 是 $\mathbb{R}^2$ 中按正向取向的可整曲线（Jordan 曲线），并满足： $$ \Gamma_i \subset R_0, \quad \text{当 } 1 \leq i \leq n,~ $$ $$ \Gamma_i \subset \mathbb{R}^2 \setminus \overline{R}_j, \quad \text{当 } 1 \leq i, j \leq n \text{ 且 } i \neq j,~ $$ 其中 $R_i$ 表示 $\Gamma_i$ 的内区域。

　　 定义： $$ D = R_0 \setminus (\overline{R}_1 \cup \overline{R}_2 \cup \cdots \cup \overline{R}_n)~ $$ 假设函数：$p: \overline{D} \to \mathbb{R}, \quad q: \overline{D} \to \mathbb{R}$ 在区域 $\overline{D}$ 上连续，并且在 $D$ 内是 Fréchet 可微的。若函数： $$ (x, y) \longmapsto \frac{\partial q}{\partial e_1}(x, y) - \frac{\partial p}{\partial e_2}(x, y)~ $$ 在 $D$ 上是黎曼可积的，则有： $$ \int_{\Gamma_0} p(x, y)\,dx + q(x, y)\,dy - \sum_{i=1}^n \int_{\Gamma_i} p(x, y)\,dx + q(x, y)\,dy = \int_D \left\{ \frac{\partial q}{\partial e_1}(x, y) - \frac{\partial p}{\partial e_2}(x, y) \right\} \, d(x, y)~ $$

7. 与斯托克斯定理的关系

　　 格林定理是凯尔文–斯托克斯定理在 $xy$ 平面区域上的一个特例。

　　 可以将二维向量场扩展成一个三维向量场，其 $z$ 分量恒为 $0$。设向量函数：$\mathbf{F} = (L, M, 0)$。从格林定理的左边开始： $$ \oint_C (L\,dx + M\,dy) = \oint_C (L, M, 0) \cdot (dx, dy, dz) = \oint_C \mathbf{F} \cdot d\mathbf{r}~ $$ 凯尔文–斯托克斯定理为： $$ \oint_C \mathbf{F} \cdot d\mathbf{r} = \iint_S \nabla \times \mathbf{F} \cdot \mathbf{\hat{n}} \, dS~ $$ 这里的曲面 $S$ 正是平面区域 $D$，其单位法向量 $\mathbf{\hat{n}}$ 依照惯例取 $z$ 分量为正，以保证与两个定理中 “正向取向” 的定义一致。

　　 积分内部的表达式为： $$ \nabla \times \mathbf{F} \cdot \mathbf{\hat{n}} = \left[ \left(\frac{\partial 0}{\partial y} - \frac{\partial M}{\partial z}\right)\mathbf{i} + \left(\frac{\partial L}{\partial z} - \frac{\partial 0}{\partial x}\right)\mathbf{j} + \left(\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y}\right)\mathbf{k} \right] \cdot \mathbf{k} = \left(\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y}\right)~ $$ 因此，得出格林定理右边的表达式： $$ \iint_S \nabla \times \mathbf{F} \cdot \mathbf{\hat{n}} \, dS = \iint_D \left(\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y}\right) \, dA~ $$ 利用微分形式和外微分，格林定理也可以直接从一般的斯托克斯定理推导出来： $$ \oint_C L\,dx + M\,dy = \oint_{\partial D} \omega = \int_D d\omega = \int_D \frac{\partial L}{\partial y} \, dy \wedge dx + \frac{\partial M}{\partial x} \, dx \wedge dy = \iint_D \left(\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y}\right) dx\,dy~ $$

8. 与散度定理的关系

　　 仅考虑二维向量场时，格林定理等价于二维形式的散度定理： $$ \iint_D \left(\nabla \cdot \mathbf{F} \right) dA = \oint_C \mathbf{F} \cdot \mathbf{\hat{n}} \, ds,~ $$ 其中，$\nabla \cdot \mathbf{F}$ 是二维向量场 $\mathbf{F}$ 的散度，$\mathbf{\hat{n}}$ 是边界曲线上的外向单位法向量。

　　 要看出这一点，可以先考察方程右边的单位法向量 $\mathbf{\hat{n}}$。在格林定理中，曲线切向微元 $d\mathbf{r} = (dx, dy)$ 指向沿曲线 $C$ 的切线方向，且 $C$ 按正向（逆时针）取向，因此外法向方向应当与切向向量右转 90° 的方向一致。一个合适的选择是向量 $(dy, -dx)$。该向量的长度为：$\sqrt{dx^2 + dy^2} = ds$，即曲线长度微元。因此可以写成：$(dy, -dx) = \mathbf{\hat{n}} \, ds$。

　　 从格林定理左边的积分出发： $$ \oint_C (L\,dx + M\,dy) = \oint_C (M, -L) \cdot (dy, -dx) = \oint_C (M, -L) \cdot \mathbf{\hat{n}} \, ds~ $$ 若取 $\mathbf{F} = (M, -L)$，应用二维散度定理，就得到： $$ \oint_C (M, -L) \cdot \mathbf{\hat{n}} \, ds = \iint_D \left(\nabla \cdot (M, -L)\right) dA = \iint_D \left( \frac{\partial M}{\partial x} - \frac{\partial L}{\partial y} \right) dA~ $$ 这正好对应格林定理的右侧，从而说明格林定理确实是二维散度定理的一个特例。

9. 面积计算

　　 格林定理可以通过线积分来计算平面区域的面积。\(^\text{[4]}\) 平面区域 $D$ 的面积为： $$ A = \iint_D dA~ $$ 选择 $L$ 和 $M$ 使得：$\frac{\partial M}{\partial x} - \frac{\partial L}{\partial y} = 1$ 则区域的面积可以表示为： $$ A = \oint_C (L\,dx + M\,dy)~ $$ 对于区域 $D$，面积的几种常见公式包括 \(^\text{[4]}\)： $$ A = \oint_C x\,dy = -\oint_C y\,dx = \frac{1}{2} \oint_C (-y\,dx + x\,dy)~ $$

10. 历史

　　 该定理以乔治·格林 的名字命名。他在 1828 年的一篇论文《An Essay on the Application of Mathematical Analysis to the Theories of Electricity and Magnetism》（《数学分析在电学和磁学理论中的应用》）中提出了类似的结果。1846 年，奥古斯丁-路易·柯西发表了一篇论文，将格林定理以现代教材中的形式写成了倒数第二句话。这也是该定理以现代形式首次出现在印刷出版物中的版本。乔治·格林在 1828 年的论文中并没有直接推导出本文所述形式的 “格林定理”，而是推导出了 “散度定理” 的一种形式，该内容出现在论文第 10–12 页。

　　 1846 年，本文中所见形式的 “格林定理” 首次以无证明的形式，由柯西在一篇题为《Sur les intégrales qui s'étendent à tous les points d'une courbe fermée》（《关于延伸至封闭曲线所有点的积分》）的文章中发表在《Comptes rendus》第 23 卷 251–255 页。该公式出现在第 254 页底部，其中 (S) 表示曲线 $s$ 围成区域 $S$ 上函数 $k$ 的线积分。伯恩哈德·黎曼 在 1851 年的博士毕业论文《Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse》（《复变函数通论基础》）中，首次给出了该定理的完整证明。此论文于 1867 年由德国哥廷根的 Adalbert Rente 出版，相关内容见第 8–9 页。\(^\text{[5]}\)

11. 参见

• 平面面积计：用于测量面积的工具
• 镜像电荷法：静电学中利用唯一性定理（由格林定理推导）的方法
• 鞋带公式：格林定理在简单多边形上的特例
• Desmos：基于网页的图形计算器

12. 参考文献

1. Riley, Kenneth F.; Hobson, Michael P.; Bence, Stephen J. (2010). Mathematical methods for physics and engineering (第 3 版). 剑桥：剑桥大学出版社. ISBN 978-0-521-86153-3.
2. Lipschutz, Seymour; Spiegel, Murray R. (2009). Vector analysis and an introduction to tensor analysis. Schaum's outline series (第 2 版). 纽约：McGraw Hill Education. ISBN 978-0-07-161545-7. OCLC 244060713.
3. Apostol, Tom (1960). Mathematical Analysis. 马萨诸塞州雷丁：Addison-Wesley. OCLC 6699164.
4. Stewart, James (1999). Calculus. GWO - A Gary W. Ostedt book (第 4 版). Pacific Grove, Calif. London: Brooks/Cole. ISBN 978-0-534-35949-2.
5. Katz, Victor J. (2009). “22.3.3: Complex Functions and Line Integrals”. A history of mathematics: an introduction (第 3 版, PDF). 波士顿、慕尼黑：Addison-Wesley. 第 801–805 页. ISBN 978-0-321-38700-4.

13. 延伸阅读

• Marsden, Jerrold E.; Tromba, Anthony (2003). “The Integral Theorems of Vector Analysis”. Vector calculus (第 5 版). 纽约：W\.H. Freeman. 第 518–608 页. ISBN 978-0-7167-4992-9.

14. 外部链接

• [MathWorld 上的格林定理](https://mathworld.wolfram.com/GreensTheorem.html)