泰勒公式（综述）

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

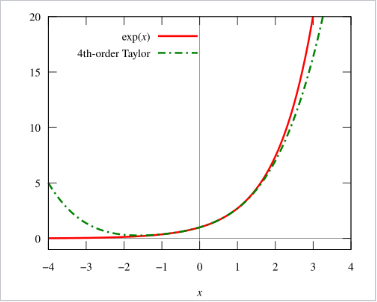
　　 在微积分中，泰勒定理给出了一个 \( k \) 次可导函数在某个给定点的近似，通过一个 \( k \) 次多项式，称为 \( k \) 阶泰勒多项式。对于一个光滑函数，泰勒多项式是该函数泰勒级数在 \( k \) 阶的截断。一级泰勒多项式是该函数的线性近似，二级泰勒多项式通常称为二次近似 \(^\text{[1]}\)。泰勒定理有多个版本，其中一些版本给出了函数通过其泰勒多项式近似的误差的明确估计。

　　 泰勒定理以数学家布鲁克·泰勒命名，他在 1715 年提出了该定理的一个版本，\(^\text{[2]}\) 尽管早在 1671 年，詹姆斯·格雷戈里就已提到过该结果的早期版本 \(^\text{[3]}\)。

　　 泰勒定理在初级微积分课程中教授，是数学分析中的一个核心基本工具。它提供了简单的算术公式，用于准确计算许多超越函数的值，如指数函数和三角函数。它是解析函数研究的起点，并在数学的各个领域、数值分析以及数学物理中具有基础性意义。泰勒定理也可以推广到多变量和向量值函数。它为一些开创性的早期计算机提供了数学基础：查尔斯·巴贝奇的差分机通过数值积分其泰勒级数的前七项来计算正弦、余弦、对数和其他超越函数。

1. 动机

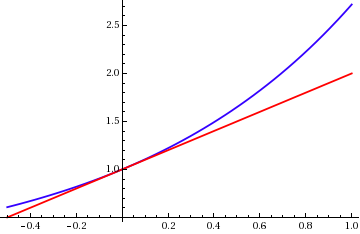
　　 如果实值函数 \( f(x) \) 在点 \( x = a \) 处可导，那么它在该点附近有一个线性近似。也就是说，存在一个函数 \( h_1(x) \)，使得 \[ f(x) = f(a) + f'(a)(x - a) + h_1(x)(x - a), \quad \lim_{x \to a} h_1(x) = 0.~ \] 这里， \[ P_1(x) = f(a) + f'(a)(x - a)~ \] 是 \( f(x) \) 在 \( x \) 接近点 \( a \) 时的线性近似，其图像 \( y = P_1(x) \) 是 \( y = f(x) \) 在 \( x = a \) 处的切线。近似的误差是：\(R_1(x) = f(x) - P_1(x) = h_1(x)(x - a)\).

　　 当 \( x \) 趋近于 \( a \) 时，这个误差比 \( (x - a) \) 收敛得更快，这使得 \( f(x) \approx P_1(x) \) 成为一个有用的近似。

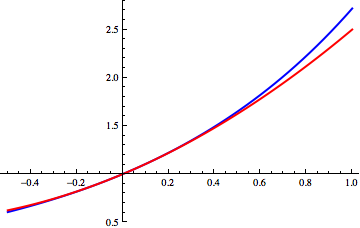
　　 为了更好地近似 \( f(x) \)，我们可以拟合一个二次多项式，而不是线性函数： \[ P_2(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2}(x - a)^2.~ \] 这个多项式不仅匹配了 \( f(x) \) 在 \( x = a \) 处的一阶导数，而且匹配了二阶导数，正如通过微分可以看出的一样。

　　 泰勒定理确保了在 \( x = a \) 的足够小邻域内，二次近似比线性近似更准确。具体来说， \[ f(x) = P_2(x) + h_2(x)(x - a)^2, \quad \lim_{x \to a} h_2(x) = 0.~ \] 这里，近似的误差是 \[ R_2(x) = f(x) - P_2(x) = h_2(x)(x - a)^2,~ \] 考虑到 \( h_2 \) 的极限行为，随着 \( x \) 趋近于 \( a \)，这个误差比 \( (x - a)^2 \) 收敛得更快。

　　 类似地，如果我们使用更高阶的多项式来近似 \( f \)，我们可能得到更好的近似，因为这样我们可以在选定的基点匹配更多的导数。

　　 一般来说，通过一个 \( k \) 次多项式近似函数时，误差会比 \( (x - a)^k \) 收敛得更快，随着 \( x \) 趋近于 \( a \)。然而，也存在一些函数，即使是无限可导的函数，对于这些函数，增加近似多项式的阶数并不会提高近似的准确度：我们说这样的函数在 \( x = a \) 处不具备解析性：它不能仅通过该点的导数来（局部）确定。

　　 泰勒定理具有渐近性质：它仅告诉我们，使用 \( k \) 阶泰勒多项式 \( P_k \) 近似时，误差 \( R_k \) 相对于任何非零的 \( k \) 次多项式，随着 \( x \to a \) 时趋向零的速度更快。它并没有告诉我们在扩展中心的任何具体邻域内误差有多大，但为此目的，存在针对余项的明确公式（如下所示），这些公式在对 \( f \) 进行某些额外规则性假设时有效。这些增强版的泰勒定理通常会在扩展中心的一个小邻域内提供对近似误差的统一估计，但这些估计不一定适用于过大的邻域，即使函数 \( f \) 是解析的。在这种情况下，可能需要选择多个具有不同扩展中心的泰勒多项式，才能对原始函数进行可靠的泰勒近似（参见图 4 的动画）。

　　 我们可以通过余项来使用几种方法：

1. 估计误差：对于一个度数为 \( k \) 的多项式 \( P_k(x) \)，在给定的区间 \( (a - r, a + r) \) 上近似 \( f(x) \) 时，估计误差。（给定区间和度数，我们可以找到误差。）
2. 找到最小的度数 \( k \)，使得多项式 \( P_k(x) \) 在给定区间 \( (a - r, a + r) \) 上能够将 \( f(x) \) 近似到给定的误差容限内。（给定区间和误差容限，我们可以找到度数。）
3. 找到最大的区间 \( (a - r, a + r) \)，使得 \( P_k(x) \) 在该区间内将 \( f(x) \) 近似到给定的误差容限内。（给定度数和误差容限，我们可以找到区间。）

2. 一元实变量的泰勒定理

定理的陈述

　　 泰勒定理最基本版本的精确陈述如下：.

　　 泰勒定理 \(^\text{[4][5][6]}\)— 设 \( k \geq 1 \) 是整数，且函数 \( f : R\to R\) 在点 \(a \in R\) 处 \( k \) 次可导。则存在一个函数 \( h_k : R\to R\)，使得 \[ f(x) = \sum_{i=0}^{k} \frac{f^{(i)}(a)}{i!} (x - a)^i + h_k(x)(x - a)^k,~ \] 且 \[ \lim_{x \to a} h_k(x) = 0.~ \] 这称为余项的佩阿诺形式。

　　 在泰勒定理中出现的多项式是函数 \( f \) 在点 \( a \) 处的 \( k \) 阶泰勒多项式 \[ P_k(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \cdots + \frac{f^{(k)}(a)}{k!}(x - a)^k~ \] 泰勒多项式是唯一的 “渐近最佳拟合” 多项式，意味着如果存在一个函数 \( h_k : \mathbf{R} \to \mathbf{R}\) 和一个 \( k \) 阶多项式 \( p \)，使得 \[ f(x) = p(x) + h_k(x)(x - a)^k, \quad \lim_{x \to a} h_k(x) = 0,~ \] 则 \( p = P_k \)。泰勒定理描述了余项的渐近行为 \[ R_k(x) = f(x) - P_k(x),~ \] 这是使用泰勒多项式近似 \( f \) 时的近似误差。使用小 \( o \) 符号，泰勒定理中的表述为 \[ R_k(x) = o(|x - a|^k), \quad x \to a.~ \]

余项的明确公式

　　 在对函数 \( f \) 进行更强的规则性假设下，存在几个精确的泰勒多项式余项 \( R_k \) 的公式，最常见的公式如下。

　　 余项的均值形式—设 \( f :\mathbf{R} \to \mathbf{R} \) 在 \( a \) 和 \( x \) 之间的开区间上是 \( k + 1 \) 次可导，并且 \( f^{(k)} \) 在 \( a \) 和 \( x \) 之间的闭区间上是连续的。\(^\text{[7]}\) 那么， \[ R_k(x) = \frac{f^{(k+1)}(\xi_L)}{(k+1)!}(x - a)^{k+1}~ \] 其中 \( \xi_L \) 是介于 \( a \) 和 \( x \) 之间的某个实数。这是余项的拉格朗日形式 \(^\text{[8]}\)。

　　 类似地， \[ R_k(x) = \frac{f^{(k+1)}(\xi_C)}{k!}(x - \xi_C)^k(x - a)~ \] 其中 \( \xi_C \) 是介于 \( a \) 和 \( x \) 之间的某个实数。这是余项的柯西形式 \(^\text{[9]}\)。

　　 两者都可以被视为以下结果的特例：考虑 \( p > 0 \) \[ R_k(x) = \frac{f^{(k+1)}(\xi_S)}{k!}(x - \xi_S)^{k+1-p} \frac{(x - a)^p}{p}~ \] 其中 \( \xi_S \) 是介于 \( a \) 和 \( x \) 之间的某个实数。这是余项的施洛米尔赫形式（有时称为施洛米尔赫-罗什形式）。当选择 \( p = k + 1 \) 时，得到的是拉格朗日形式，而当选择 \( p = 1 \) 时，得到的是柯西形式。

　　 泰勒定理的这些改进通常通过均值定理来证明，因此得名。此外，注意到当 \( k = 0 \) 时，这实际上就是均值定理。还可以找到其他类似的表达式。例如，如果 \( G(t) \) 在闭区间上连续，并且在开区间 \( (a, x) \) 上可导且导数不为零，那么 \[ R_k(x) = \frac{f^{(k+1)}(\xi)}{k!}(x - \xi)^k \frac{G(x) - G(a)}{G'(\xi)}~ \] 其中 \( \xi \) 是介于 \( a \) 和 \( x \) 之间的某个数。这一版本涵盖了余项的拉格朗日形式和柯西形式作为特例，并且使用柯西均值定理证明。通过取 \( G(t) = (x - t)^{k+1} \) 可以得到拉格朗日形式，而通过取 \( G(t) = t - a \) 可以得到柯西形式。

　　 余项的积分形式比之前的形式更为复杂，要求理解勒贝格积分理论才能实现完全的通用性。然而，它也适用于黎曼积分的意义，只要 \( f \) 的 \( (k+1) \) 阶导数在闭区间 \( [a, x] \) 上是连续的。

　　 余项的积分形式 \(^\text{[10]}\)—设 \( f^{(k)} \) 在闭区间 \( [a, x] \) 上是绝对连续的。那么 \[ R_k(x) = \int_a^x \frac{f^{(k+1)}(t)}{k!} (x - t)^k \, dt.~ \] 由于 \( f^{(k)} \) 在闭区间 \( [a, x] \) 上是绝对连续的，函数 \( f^{(k+1)} \) 作为 \( L^1 \)-函数存在，且该结果可以通过使用微积分基本定理和分部积分法进行形式化计算来证明。

余项的估计

　　 在实践中，通常需要估计泰勒近似中的余项，而不是得到其精确的公式。假设函数 \( f \) 在包含 \( a \) 的区间 \( I \) 上是 \( (k + 1) \) 次连续可导的。假设存在实数常数 \( q \) 和 \( Q \)，使得 \[ q \leq f^{(k+1)}(x) \leq Q~ \] 在整个区间 \( I \) 上成立。那么，余项满足不等式[11] \[ q \frac{(x - a)^{k+1}}{(k + 1)!} \leq R_k(x) \leq Q \frac{(x - a)^{k+1}}{(k + 1)!}~ \] 当 \( x > a \) 时，且对于 \( x < a \) 也有类似的估计。这是拉格朗日形式余项的一个简单结果。特别地，如果 \[ |f^{(k+1)}(x)| \leq M~ \] 在区间 \( I = (a - r, a + r) \) 上成立，其中 \( r > 0 \)，那么 \[ |R_k(x)| \leq M \frac{|x - a|^{k+1}}{(k+1)!} \leq M \frac{r^{k+1}}{(k+1)!}~ \] 对于所有 \( x \in (a - r, a + r) \) 都成立。第二个不等式称为一致估计，因为它对区间 \( (a - r, a + r) \) 上的所有 \( x \) 都成立。

示例

　　 假设我们希望在区间 \( [-1, 1] \) 上找到函数 \( f(x) = e^x \) 的近似值，同时确保近似误差不超过 \( 10^{-5} \)。在这个示例中，我们假设我们只知道指数函数的以下性质： \[ e^0 = 1, \quad \frac{d}{dx} e^x = e^x, \quad e^x > 0, \quad x \in \mathbb{R}.\qquad \text{(★)}~ \] 从这些性质可以得出，\( f^{(k)}(x) = e^x \) 对于所有 \( k \) 都成立，特别地，\( f^{(k)}(0) = 1 \)。因此，函数 \( f \) 在 \( 0 \) 处的 \( k \) 阶泰勒多项式及其拉格朗日形式的余项给出如下： \[ P_k(x) = 1 + x + \frac{x^2}{2!} + \cdots + \frac{x^k}{k!},~ \] \[ R_k(x) = \frac{e^\xi}{(k+1)!} x^{k+1},~ \] 其中 \( \xi \) 是介于 \( 0 \) 和 \( x \) 之间的某个数。由于 \( e^x \) 是递增的（根据公式★），我们可以直接使用 \( e^x \leq 1 \) 对于 \( x \in [-1, 0] \) 来估计区间 \( [-1, 0] \) 上的余项。为了得到区间 \( [0, 1] \) 上余项的上界，我们使用性质 \( e^\xi < e^x \) 对于 \( 0 < \xi < x \)，从而估计： \[ e^x = 1 + x + \frac{e^\xi}{2} x^2 < 1 + x + \frac{e^x}{2} x^2, \quad 0 < x \leq 1,~ \] 使用二阶泰勒展开。然后我们求解 \( e^x \)，得出： \[ e^x \leq \frac{1 + x}{1 - \frac{x^2}{2}} = 2 \frac{1 + x}{2 - x^2} \leq 4, \quad 0 \leq x \leq 1,~ \] 通过最大化分子并最小化分母。结合这些关于 \( e^x \) 的估计，我们可以看到： \[ |R_k(x)| \leq \frac{4 |x|^{k+1}}{(k+1)!} \leq \frac{4}{(k+1)!}, \quad -1 \leq x \leq 1,~ \] 因此，当 \[ \frac{4}{(k+1)!} < 10^{-5} \quad \Longleftrightarrow \quad 4 \cdot 10^5 < (k+1)! \quad \Longleftrightarrow \quad k \geq 9,~ \] （参见阶乘或手动计算值 \( 9! = 362880 \) 和 \( 10! = 3628800 \)）。作为结论，泰勒定理得到如下近似： \[ e^x = 1 + x + \frac{x^2}{2!} + \cdots + \frac{x^9}{9!} + R_9(x), \quad |R_9(x)| < 10^{-5}, \quad -1 \leq x \leq 1.~ \] 例如，这个近似提供了一个小数表达式：\(e \approx 2.71828\)，精确到五个小数位。

3. 与解析性的关系

实值解析函数的泰勒展开

　　 设 \( I \subset \mathbf{R} \) 为开区间。根据定义，函数 \( f : I \to \mathbf{R} \) 是实值解析的，如果它可以由收敛的幂级数在局部定义。这意味着，对于每个 \( a \in I \)，存在某个 \( r > 0 \) 和一组系数 \( c_k \in \mathbf{R}\)，使得 \( (a - r, a + r) \subset I \) 并且 \[ f(x) = \sum_{k=0}^{\infty} c_k (x - a)^k = c_0 + c_1 (x - a) + c_2 (x - a)^2 + \cdots, \quad |x - a| < r.~ \] 一般来说，幂级数的收敛半径可以通过柯西–哈达玛公式来计算： \[ \frac{1}{R} = \limsup_{k \to \infty} |c_k|^{\frac{1}{k}}.~ \] 这个结果是通过与几何级数的比较得到的，使用相同的方法可以证明，如果基于 \( a \) 的幂级数对于某个 \( b \in \mathbf{R}\) 收敛，则它必须在闭区间 \( [a - r_b, a + r_b] \) 上均匀收敛，其中 \( r_b = |b - a| \)。这里只考虑幂级数的收敛性，并且可能 \( (a - R, a + R) \) 会超出函数 \( f \) 的定义域 \( I \)。

　　 实值解析函数 \( f \) 在点 \( a \) 处的泰勒多项式只是其局部定义幂级数的有限截断： \[ P_k(x) = \sum_{j=0}^{k} c_j (x - a)^j, \quad c_j = \frac{f^{(j)}(a)}{j!}.~ \] 相应的余项在局部上由解析函数给出： \[ R_k(x) = \sum_{j=k+1}^{\infty} c_j (x - a)^j = (x - a)^k h_k(x), \quad |x - a| < r.~ \] 这里，函数 \[ h_k : (a - r, a + r) \to \mathbb{R}, \quad h_k(x) = (x - a) \sum_{j=0}^{\infty} c_{k+1+j} (x - a)^j~ \] 也是解析的，因为它们的定义幂级数与原始级数具有相同的收敛半径。假设 \( [a - r, a + r] \subset I \) 且 \( r < R \)，所有这些级数在 \( (a - r, a + r) \) 上均匀收敛。自然地，在解析函数的情况下，人们可以通过在展开中心的导数序列 \( f^{'}(a) \) 的尾项来估计余项 \( R_k(x) \)，但使用复分析还提供了另一种可能性，下面将描述这种方法。

泰勒定理与泰勒级数的收敛

　　 函数 \( f \) 的泰勒级数将在某个区间内收敛，在该区间内，函数的所有导数都是有界的，并且随着 \( k \) 趋近于无穷大时，它们不会增长得太快。（然而，即使泰勒级数收敛，它也可能不收敛到 \( f \)，如下面所解释的那样；这种情况下，\( f \) 被称为非解析函数。）

　　 可以将泰勒级数 \[ f(x) \approx \sum_{k=0}^{\infty} c_k (x - a)^k = c_0 + c_1 (x - a) + c_2 (x - a)^2 + \cdots~ \] 看作是函数 \( f : \mathbf{R} \to \mathbf{R} \) 在点 \( a \) 处的 “无限阶泰勒多项式”。现在，余项的估计表明，如果对于任意的 \( r \)，函数 \( f \) 的导数在区间 \( (a - r, a + r) \) 上是有界的，那么对于任何阶数 \( k \) 和任意 \( r > 0 \)，都存在常数 \( M_{k,r} > 0 \)，使得 \[ |R_k(x)| \leq M_{k,r} \frac{|x - a|^{k+1}}{(k+1)!} \qquad \text{(★★)}~ \] 对于所有 \( x \in (a - r, a + r) \) 都成立。有时可以选择常数 \( M_{k,r} \)，使得对于固定的 \( r \) 和所有 \( k \)，\( M_{k,r} \) 是有上界的。此时，函数 \( f \) 的泰勒级数在某个解析函数上均匀收敛： \[ T_f : (a - r, a + r) \to \mathbb{R},~ \] \[ T_f(x) = \sum_{k=0}^{\infty} \frac{f^{(k)}(a)}{k!} (x - a)^k~ \] （即使 \( M_{k,r} \) 没有上界，只要它增长得足够慢，级数仍然会收敛。）

　　 极限函数 \( T_f \) 根据定义始终是解析的，但即使 \( f \) 是无限可导的，它也不一定等于原始函数 \( f \)。在这种情况下，我们说 \( f \) 是一个非解析的光滑函数，例如一个平坦函数： \[ f : \mathbb{R} \to \mathbb{R},~ \] \[ f(x) = \begin{cases} e^{-\frac{1}{x^2}} & x > 0 \\ 0 & x \leq 0 \end{cases}~ \] 通过数学归纳法反复使用链式法则，可以证明，对于任何阶数 \( k \)， \[ f^{(k)}(x) = \begin{cases} \frac{p_k(x)}{x^{3k}} \cdot e^{-\frac{1}{x^2}} & x > 0 \\ 0 & x \leq 0 \end{cases}~ \] 对于某个多项式 \( p_k \)，其次数为 \( 2(k - 1) \)。函数 \( e^{-\frac{1}{x^2}} \) 的收敛速度比任何多项式都快，当 \( x \to 0 \) 时，因此 \( f \) 是无限可导的，并且对于每个正整数 \( k \)，有 \( f^{(k)}(0) = 0 \)。上述结果在这种情况下都成立：

1. \( f \) 的泰勒级数均匀收敛到零函数 \( T_f(x) = 0 \)，该函数是解析的，所有系数都等于零。
2. 函数 \( f \) 不等于这个泰勒级数，因此是非解析的。
3. 对于任意阶数 \( k \in \mathbf{N} \) 和半径 \( r > 0 \)，存在 \( M_{k,r} > 0 \) 满足余项界限（★★）。

　　 然而，当 \( k \) 增加时，对于固定的 \( r \)，\( M_{k,r} \) 的值增长得比 \( r^k \) 快，导致误差不趋近于零。

复分析中的泰勒定理

　　 泰勒定理可以推广到在复平面开子集 \( U \subset \mathbf{C}\) 上复可导的函数 \( f : \mathbf{C}\to \mathbf{C} \)。然而，它的实用性被复分析中的其他一般定理所超越。即，使用柯西积分公式，可以推导出复可导函数 \( f : U \to \mathbf{C}\) 的相关结果的更强版本，如下所示。

　　 设 \( r > 0 \)，使得闭圆盘 \( B(z, r) \cup S(z, r) \) 被包含在 \( U \) 中。然后，柯西积分公式给出： \[ f(z) = \frac{1}{2\pi i} \int_{\gamma} \frac{f(w)}{w - z} \, dw,~ \] \[ f'(z) = \frac{1}{2\pi i} \int_{\gamma} \frac{f(w)}{(w - z)^2} \, dw,~ \] \[ \ldots,~ \] \[ f^{(k)}(z) = \frac{k!}{2\pi i} \int_{\gamma} \frac{f(w)}{(w - z)^{k+1}} \, dw.~ \] 这里，\( \gamma(t) = z + re^{it} \) 是圆 \( S(z, r) \) 的正向参数化，且 \( t \in [0, 2\pi] \)。

　　 这里所有的被积函数在圆 \( S(z, r) \) 上都是连续的，这就证明了可以在积分符号下进行微分。特别地，如果 \( f \) 在开集 \( U \) 上一次复可导，那么它实际上在 \( U \) 上是无限次复可导的。还可以得到柯西估计 \(^\text{[12]}\)： \[ |f^{(k)}(z)| \leq \frac{k!}{2\pi} \int_{\gamma} \frac{M_r}{|w - z|^{k+1}} \, dw = \frac{k! M_r}{r^k}, \quad M_r = \max_{|w - c| = r} |f(w)|~ \] 对于任何 \( z \in U \) 和 \( r > 0 \)，使得 \( B(z, r) \cup S(c, r) \subset U \)。该估计意味着复泰勒级数 \[ T_f(z) = \sum_{k=0}^{\infty} \frac{f^{(k)}(c)}{k!} (z - c)^k~ \] 对任意开圆盘 \( B(c, r) \subset U \) 且 \( S(c, r) \subset U \) 上均匀收敛到某个函数 \( T_f \)。此外，使用导数 \( f^{(k)}(c) \) 的轮廓积分公式， \[ \begin{aligned} T_f(z) &= \sum_{k=0}^{\infty} \frac{(z - c)^k}{2\pi i} \int_{\gamma} \frac{f(w)}{(w - c)^{k+1}} \, dw \\ &= \frac{1}{2\pi i} \int_{\gamma} \frac{f(w)}{w - c} \sum_{k=0}^{\infty} \left( \frac{z - c}{w - c} \right)^k \, dw \\ &= \frac{1}{2\pi i} \int_{\gamma} \frac{f(w)}{w - c} \left( \frac{1}{1 - \frac{z - c}{w - c}} \right) \, dw \\ &= \frac{1}{2\pi i} \int_{\gamma} \frac{f(w)}{w - z} \, dw \\ &= f(z), \end{aligned}~ \] 因此，任何在开集 \( U \subset C \) 上复可导的函数 \( f \) 实际上是复解析的。这里提到的关于实值解析函数的所有内容，同样适用于复值解析函数，只需将开区间 \( I \) 替换为开子集 \( U \in C \)，并将以 \( a \) 为中心的区间 \( (a - r, a + r) \) 替换为以 \( c \) 为中心的圆盘 \( B(c, r) \)。特别地，泰勒展开式的形式为： \[ f(z) = P_k(z) + R_k(z), \quad P_k(z) = \sum_{j=0}^{k} \frac{f^{(j)}(c)}{j!} (z - c)^j,~ \]

　　 其中余项 \( R_k \) 是复解析的。复分析的方法提供了一些强有力的结果，涉及泰勒展开。例如，使用柯西积分公式，对于任何正向参数化的乔丹曲线 \( \gamma \)，其参数化边界 \( \partial W \subset U \) 的区域 \( W \subset U \)，可以得到如上所示的导数 \( f^{(j)}(c) \) 的表达式，并通过稍微修改 \( T_f(z) = f(z) \) 的计算，可以得到精确的公式： \[ R_k(z) = \sum_{j=k+1}^{\infty} \frac{(z - c)^j}{2\pi i} \int_{\gamma} \frac{f(w)}{(w - c)^{j+1}} \, dw = \frac{(z - c)^{k+1}}{2\pi i} \int_{\gamma} \frac{f(w) \, dw}{(w - c)^{k+1} (w - z)}, \quad z \in W.~ \] 这里的重要特点是，泰勒多项式在区域 \( W \subset U \) 上的近似质量由函数 \( f \) 在边界 \( \partial W \subset U \) 上的值主导。类似地，应用柯西估计到余项的级数表达式，我们可以得到均匀估计： \[ |R_k(z)| \leq \sum_{j=k+1}^{\infty} \frac{M_r |z - c|^j}{r^j} = \frac{M_r}{r^{k+1}} \frac{|z - c|^{k+1}}{1 - \frac{|z - c|}{r}} \leq \frac{M_r \beta^{k+1}}{1 - \beta}, \quad \frac{|z - c|}{r} \leq \beta < 1.~ \]

示例

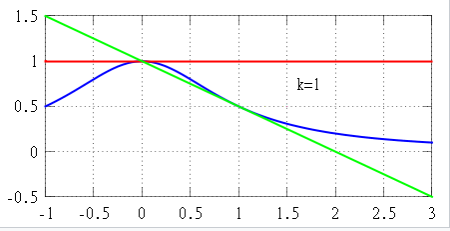
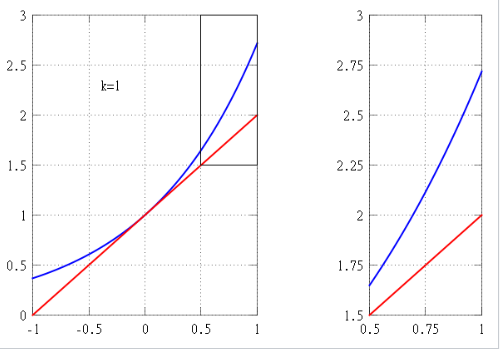
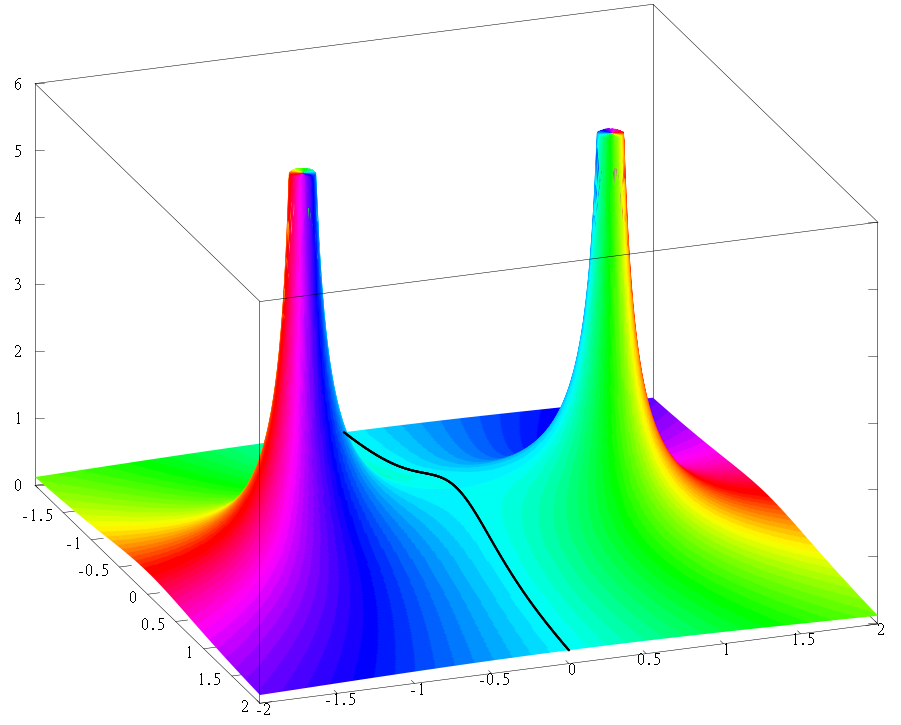
　　 函数 \[ f : \mathbb{R} \to \mathbb{R},~ \] \[ f(x) = \frac{1}{1 + x^2}~ \] 是实值解析的，也就是说，它在局部上由其泰勒级数确定。该函数在上面已绘制，旨在说明某些初等函数在展开中心的邻域内不能通过泰勒多项式进行近似，尤其是当邻域过大时。这种行为在复分析框架中容易理解。具体来说，函数 \( f \) 可以扩展为一个有理函数 \[ f : \mathbb{C} \cup \{\infty\} \to \mathbb{C} \cup \{\infty\},~ \] \[ f(z) = \frac{1}{1 + z^2}~ \] 在紧化的复平面上。它在 \( z = i \) 和 \( z = -i \) 处有简单极点，并且在其他地方是解析的。现在，它以 \( z_0 \) 为中心的泰勒级数在任何 \( B(z_0, r) \) 上收敛，其中 \( r < |z - z_0| \)，且相同的泰勒级数在 \( z \in \mathbf{C} \) 处收敛。因此，\( f \) 在 \( 0 \) 处的泰勒级数在 \( B(0, 1) \) 上收敛，但对于任何 \( z \in \mathbf{C} \) 且 \( |z| > 1 \)，它都不收敛，因为存在极点 \( i \) 和 \( -i \)。出于相同的原因，\( f \) 在 \( 1 \) 处的泰勒级数在 \( B(1, \sqrt{2}) \) 上收敛，但对于任何 \( z \in \mathbf{C} \) 且 \( |z - 1| > \sqrt{2} \)，它也不收敛。

4. 泰勒定理的推广

高阶可导性

　　 函数 \( f : \mathbf{R}^n \to \mathbf{R} \) 在 \( a \in \mathbf{R}^n \) 处可导，当且仅当存在一个线性泛函 \( L : \mathbf{R}^n \to \mathbf{R} \) 和一个函数 \( h : \mathbf{R}^n \to \mathbf{R} \)，使得 \[ f(\mathbf{x}) = f(\mathbf{a}) + L(\mathbf{x} - \mathbf{a}) + h(\mathbf{x}) \|\mathbf{x} - \mathbf{a}\|, \quad \lim_{\mathbf{x} \to \mathbf{a}} h(\mathbf{x}) = 0.~ \] 如果是这种情况，那么 \( L = df(\mathbf{a}) \) 是 \( f \) 在点 \( a \) 处的（唯一确定的）微分。此外，\( f \) 的偏导数在 \( a \) 处存在，且 \( f \) 在 \( a \) 处的微分为 \[ df(\mathbf{a})(\mathbf{v}) = \frac{\partial f}{\partial x_1}(\mathbf{a}) v_1 + \cdots + \frac{\partial f}{\partial x_n}(\mathbf{a}) v_n.~ \] 引入多重下标符号： \[ |\alpha| = \alpha_1 + \cdots + \alpha_n, \quad \alpha! = \alpha_1! \cdots \alpha_n!, \quad \mathbf{x}^{\alpha} = x_1^{\alpha_1} \cdots x_n^{\alpha_n}~ \] 对于 \( \alpha \in \mathbf{N}^n \) 和 \( \mathbf{x} \in \mathbf{R}^n \)。如果函数 \( f : \mathbf{R}^n \to \mathbf{R} \) 的所有 \( k \)-阶偏导数在 \( a \in \mathbf{R}^n \) 处是连续的，那么根据克莱朗定理，可以交换混合导数的顺序，因此在这种情况下，符号 \[ D^{\alpha} f = \frac{\partial^{|\alpha|} f}{\partial \mathbf{x}^{\alpha}} = \frac{\partial^{\alpha_1 + \cdots + \alpha_n} f}{\partial x_1^{\alpha_1} \cdots \partial x_n^{\alpha_n}}~ \] 用于高阶偏导数是合理的。如果 \( f \) 的所有 \( (k-1) \)-阶偏导数在点 \( a \) 的某个邻域内存在并且在 \( a \) 处是可导的 \(^\text{[13]}\)，那么我们说 \( f \) 在点 \( a \) 处是 \( k \) 次可导的。

多元函数的泰勒定理

　　 使用前一节的符号，得出以下定理。

　　 多元泰勒定理版本 \(^\text{[14]}\)—设 \( f : \mathbf{R}^n \to \mathbf{R} \) 是在点 \( a \in \mathbf{R}^n \) 处 \( k \) 次连续可导的函数。那么，存在函数 \( h_\alpha : \mathbf{R}^n \to \mathbf{R} \)，其中 \( |\alpha| = k \)，使得 \[ f(\mathbf{x}) = \sum_{|\alpha| \leq k} \frac{D^\alpha f(\mathbf{a})}{\alpha!} (\mathbf{x} - \mathbf{a})^\alpha + \sum_{|\alpha| = k} h_\alpha(\mathbf{x}) (\mathbf{x} - \mathbf{a})^\alpha,~ \] 且 \[ \lim_{\mathbf{x} \to \mathbf{a}} h_\alpha(\mathbf{x}) = 0.~ \] 如果函数 \( f : \mathbf{R}^n \to \mathbf{R} \) 在闭球 \( B = \{ \mathbf{y} \in \mathbb{R}^n : \|\mathbf{a} - \mathbf{y}\| \leq r \} \) 内 \( k + 1 \) 次连续可导，其中 \( r > 0 \)，则可以推导出余项的精确公式，该公式以 \( f \) 的 \( (k+1) \)-阶偏导数在该邻域内的形式表示。\(^\text{[15]}\) 即， \[ f(\mathbf{x}) = \sum_{|\alpha| \leq k} \frac{D^\alpha f(\mathbf{a})}{\alpha!} (\mathbf{x} - \mathbf{a})^\alpha + \sum_{|\beta| = k+1} R_\beta(\mathbf{x}) (\mathbf{x} - \mathbf{a})^\beta,~ \] \[ R_\beta(\mathbf{x}) = \frac{|\beta|}{\beta!} \int_0^1 (1 - t)^{|\beta| - 1} D^\beta f\left( \mathbf{a} + t (\mathbf{x} - \mathbf{a}) \right) \, dt.~ \] 在这种情况下，由于 \( (k+1) \)-阶偏导数在紧集 \( B \) 中是连续的，立即可以得到均匀估计： \[ |R_\beta(\mathbf{x})| \leq \frac{1}{\beta!} \max_{|\alpha| = |\beta|} \max_{\mathbf{y} \in B} |D^\alpha f(\mathbf{y})|, \quad \mathbf{x} \in B.~ \]

二维中的示例

　　 例如，平滑函数 \( f : \mathbb{R}^2 \to \mathbb{R} \) 的三阶泰勒多项式是，记 \(\mathbf{x} - \mathbf{a} = \mathbf{v} \)， \[ P_3(\mathbf{x}) = f(\mathbf{a}) + \frac{\partial f}{\partial x_1}(\mathbf{a}) v_1 + \frac{\partial f}{\partial x_2}(\mathbf{a}) v_2 + \frac{\partial^2 f}{\partial x_1^2}(\mathbf{a}) \frac{v_1^2}{2!} + \frac{\partial^2 f}{\partial x_1 \partial x_2}(\mathbf{a}) v_1 v_2 + \frac{\partial^2 f}{\partial x_2^2}(\mathbf{a}) \frac{v_2^2}{2!} ~ \] \[ + \frac{\partial^3 f}{\partial x_1^3}(\mathbf{a}) \frac{v_1^3}{3!} + \frac{\partial^3 f}{\partial x_1^2 \partial x_2}(\mathbf{a}) \frac{v_1^2 v_2}{2!} + \frac{\partial^3 f}{\partial x_1 \partial x_2^2}(\mathbf{a}) \frac{v_1 v_2^2}{2!} + \frac{\partial^3 f}{\partial x_2^3}(\mathbf{a}) \frac{v_2^3}{3!}.~ \]

5. 证明

　　 泰勒定理在一维实变量的证明 设 \(^\text{[16]}\) \[ h_k(x) = \begin{cases} \frac{f(x) - P(x)}{(x - a)^k} & x \neq a \\ 0 & x = a \end{cases}~ \] 其中，和泰勒定理的陈述一样， \[ P(x) = f(a) + f'(a)(x - a) + \frac{f''(a)}{2!}(x - a)^2 + \cdots + \frac{f^{(k)}(a)}{k!}(x - a)^k.~ \] 我们需要证明： \[ \lim_{x \to a} h_k(x) = 0.~ \] 此证明基于反复应用洛必达法则。注意，对于每个 \( j = 0, 1, \dots, k-1 \)，都有 \(f^{(j)}(a) = P^{(j)}(a)\).因此，\( h_k(x) \) 中分子前 \( k - 1 \) 阶的导数在 \( x = a \) 处为零，分母也是如此。此外，由于函数 \( f \) 在某点 \( a \) 处是 \( k \) 次可导的，意味着在该点的邻域内需要有 \( k - 1 \) 阶导数（这是成立的，因为可导性要求函数在该点的整个邻域内定义），因此分子及其前 \( k - 2 \) 阶导数在 \( a \) 的邻域内是可导的。显然，分母也满足该条件，并且除非 \( x = a \)，否则不为零，因此所有洛必达法则所需的条件都已满足，使用洛必达法则是合理的。所以 \[ \begin{aligned} \lim_{x \to a} \frac{f(x) - P(x)}{(x - a)^k} &= \lim_{x \to a} \frac{\frac{d}{dx} (f(x) - P(x))}{\frac{d}{dx} (x - a)^k} \\ &= \cdots \\ &= \lim_{x \to a} \frac{\frac{d^{k-1}}{dx^{k-1}} (f(x) - P(x))}{\frac{d^{k-1}}{dx^{k-1}} (x - a)^k}\\ &= \frac{1}{k!} \lim_{x \to a} \frac{f^{(k-1)}(x) - P^{(k-1)}(x)}{x - a} \\ &= \frac{1}{k!} (f^{(k)}(a) - P^{(k)}(a)) = 0, \end{aligned}~ \] 其中倒数第二个等式是根据导数在 \( x = a \) 处的定义得到的。

泰勒定理的一种替代证明

　　 设 \( f(x) \) 为任何实值连续函数，旨在通过泰勒多项式进行近似。

　　 步骤 1：设 \( F \) 和 \( G \) 为函数。定义 \( F \) 和 \( G \) 为： \[ F(x) = f(x) - \sum_{k=0}^{n-1} \frac{f^{(k)}(a)}{k!} (x - a)^k~ \] \[ G(x) = (x - a)^n~ \]

　　 步骤 2:\( F \) 和 \( G \) 的性质：

　　 \[ F(a) = f(a) - f(a) - f'(a)(a - a) - \cdots - \frac{f^{(n-1)}(a)}{(n-1)!} (a - a)^{n-1} = 0~ \] \[ G(a) = (a - a)^n = 0~ \] 类似地， \[ F'(a) = f'(a) - f'(a) - \frac{f''(a)}{(2-1)!}(a - a)^{(2-1)} - \cdots - \frac{f^{(n-1)}(a)}{(n-2)!}(a - a)^{n-2} = 0~ \] \[ G'(a) = n(a - a)^{n-1} = 0~ \] \[ \vdots~ \] \[ G^{(n-1)}(a) = F^{(n-1)}(a) = 0~ \]

　　 步骤 3：使用柯西均值定理

　　 设 \( f_1 \) 和 \( g_1 \) 是区间 \( [a, b] \) 上的连续函数。由于 \( a < x < b \)，我们可以使用区间 \( [a, x] \) 进行操作。设 \( f_1 \) 和 \( g_1 \) 在 \( (a, x) \) 上是可导的。假设 \( g_1'(x) \neq 0 \) 对于所有 \( x \in (a, b) \)。那么，存在 \( c_1 \in (a, x) \)，使得 \[ \frac{f_1(x) - f_1(a)}{g_1(x) - g_1(a)} = \frac{f_1'(c_1)}{g_1'(c_1)}.~ \] 注意： \( G'(x) \neq 0 \) 在 \( (a, b) \) 上，并且 \( F(a), G(a) = 0 \)，所以 \[ \frac{F(x)}{G(x)} = \frac{F(x) - F(a)}{G(x) - G(a)} = \frac{F'(c_1)}{G'(c_1)}~ \] 对于某个 \( c_1 \in (a, x) \)。

　　 这也可以在 \( (a, c_1) \) 上进行： \[ \frac{F'(c_1)}{G'(c_1)} = \frac{F'(c_1) - F'(a)}{G'(c_1) - G'(a)} = \frac{F''(c_2)}{G''(c_2)}~ \] 对于某个 \( c_2 \in (a, c_1) \)。这个过程可以继续进行直到 \( c_n \)。

　　 这给出了在 \( (a, b) \) 上的划分： \[ a < c_n < c_{n-1} < \dots < c_1 < x~ \] 并且 \[ \frac{F(x)}{G(x)} = \frac{F'(c_1)}{G'(c_1)} = \dots = \frac{F^{(n)}(c_n)}{G^{(n)}(c_n)}.~ \] 设 \( c = c_n \)，则 \[ \frac{F(x)}{G(x)} = \frac{F^{(n)}(c)}{G^{(n)}(c)}.~ \]

　　 步骤 4：代回

　　 \[ \frac{F(x)}{G(x)} = \frac{f(x) - \sum_{k=0}^{n-1} \frac{f^{(k)}(a)}{k!} (x - a)^k}{(x - a)^n} = \frac{F^{(n)}(c)}{G^{(n)}(c)}~ \]

　　 根据幂法则，反复对 \( (x - a)^n \) 求导，\(G^{(n)}(c) = n(n - 1) \cdots 1\) 因此： \[ \frac{F^{(n)}(c)}{G^{(n)}(c)} = \frac{f^{(n)}(c)}{n(n - 1) \cdots 1} = \frac{f^{(n)}(c)}{n!}.~ \] 这得出： \[ f(x) - \sum_{k=0}^{n-1} \frac{f^{(k)}(a)}{k!} (x - a)^k = \frac{f^{(n)}(c)}{n!} (x - a)^n.~ \] 通过重新排列，我们得到： \[ f(x) = \sum_{k=0}^{n-1} \frac{f^{(k)}(a)}{k!} (x - a)^k + \frac{f^{(n)}(c)}{n!} (x - a)^n,~ \] 或者，因为最终 \( c_n = a \)，得： \[ f(x) = \sum_{k=0}^{n} \frac{f^{(k)}(a)}{k!} (x - a)^k.~ \]

余项均值形式的推导

　　 设 \( G \) 是在区间 \( [a, x] \) 上连续的实值函数，并且在区间 \( (a, x) \) 上可导且导数不为零，定义 \[ F(t) = f(t) + f'(t)(x - t) + \frac{f''(t)}{2!}(x - t)^2 + \cdots + \frac{f^{(k)}(t)}{k!}(x - t)^k.~ \] 对于 \( t \in [a, x] \)，根据柯西均值定理， \[ \frac{F'(\xi)}{G'(\xi)} = \frac{F(x) - F(a)}{G(x) - G(a)},\qquad \text{(★★★)}~ \] 对于某个 \( \xi \) 在 \( a \) 和 \( x \) 之间的开区间上，注意到这里分子 \( F(x) - F(a) = R_k(x) \) 恰好是泰勒多项式的余项，定义为 \( y = f(x) \)。计算： \[ F'(t) = f'(t) + \left( f''(t)(x - t) - f'(t) \right) + \left( \frac{f^{(3)}(t)}{2!} (x - t)^2 - \frac{f^{(2)}(t)}{1!} (x - t) \right) + \cdots ~ \] \[ + \left( \frac{f^{(k+1)}(t)}{k!} (x - t)^k - \frac{f^{(k)}(t)}{(k-1)!} (x - t)^{k-1} \right) = \frac{f^{(k+1)}(t)}{k!} (x - t)^k,~ \] 将其代入 (★★★) 并重新排列项，得到： \[ R_k(x) = \frac{f^{(k+1)}(\xi)}{k!} (x - \xi)^k \frac{G(x) - G(a)}{G'(\xi)}.~ \] 这是在泰勒定理陈述后提到的余项的均值形式。通过选择 \( G(t) = (x - t)^{k+1} \) 可以得到拉格朗日形式的余项，通过选择 \( G(t) = t - a \) 可以得到柯西形式的余项。

　　 备注：使用这种方法还可以通过选择

　　 \[ G(t) = \int_a^t \frac{f^{(k+1)}(s)}{k!} (x - s)^k \, ds~ \]

　　 恢复余项的积分形式，但如果希望在 \( f^{(k)} \) 仅为绝对连续的情况下证明该命题，则均值定理所需的 \( f \) 的条件太强。然而，如果使用黎曼积分而不是勒贝格积分，则假设可以得到放宽。

余项积分形式的推导

　　 由于 \( f^{(k)} \) 在闭区间 \( [a, x] \) 上的绝对连续性，\( f^{(k+1)} \) 作为 \( L^1 \)-函数存在，我们可以使用微积分基本定理和分部积分法。这同样适用于黎曼积分，假设 \( f^{(k)} \) 在闭区间上是连续的，并且在 \( (a, x) \) 上是可导的，这将得到与使用均值定理相同的结果。

　　 微积分基本定理指出： \[ f(x) = f(a) + \int_a^x f'(t) \, dt.~ \] 现在我们可以通过分部积分并再次使用微积分基本定理，得到： \[ \begin{aligned} f(x) &= f(a) + \left( x f'(x) - a f'(a) \right) - \int_a^x t f''(t) \, dt\\ &= f(a) + x \left( f'(a) + \int_a^x f''(t) \, dt \right) - a f'(a) - \int_a^x t f''(t) \, dt\\ &= f(a) + (x - a) f'(a) + \int_a^x (x - t) f''(t) \, dt, \end{aligned}~ \] 这正是泰勒定理的余项积分形式，适用于 \( k = 1 \) 的情况。通过数学归纳法可以证明一般形式。假设： \[ f(x) = f(a) + \frac{f'(a)}{1!} (x - a) + \cdots + \frac{f^{(k)}(a)}{k!} (x - a)^k + \int_a^x \frac{f^{(k+1)}(t)}{k!} (x - t)^k \, dt.\qquad \text{(eq1)}~ \] 对余项进行分部积分，我们得到： \[ \begin{aligned} \int_a^x \frac{f^{(k+1)}(t)}{k!} (x - t)^k \, dt &= -\left[ \frac{f^{(k+1)}(t)}{(k+1)k!} (x - t)^{k+1} \right]_a^x + \int_a^x \frac{f^{(k+2)}(t)}{(k+1)k!} (x - t)^{k+1} \, dt\\ &= \frac{f^{(k+1)}(a)}{(k+1)!} (x - a)^{k+1} + \int_a^x \frac{f^{(k+2)}(t)}{(k+1)!} (x - t)^{k+1} \, dt. \end{aligned}~ \] 将此代入公式 (eq1) 中，表明如果它对值 \( k \) 成立，则对值 \( k + 1 \) 也必须成立。因此，由于它对 \( k = 1 \) 成立，所以它对每个正整数 \( k \) 都成立。

多元泰勒多项式余项的推导

　　 我们证明特殊情况，其中 \( f : \mathbb{R}^n \to \mathbb{R} \) 在某个闭球 \( B \) 内具有连续的偏导数，直到 \( k+1 \) 阶，且球心为 \( \mathbf{a} \)。证明的策略是应用泰勒定理的一维版本到函数 \( f \) 在连接 \( \mathbf{x} \) 和 \( \mathbf{a} \) 的线段上的限制。[17] 将连接 \( \mathbf{a} \) 和 \( \mathbf{x} \) 的线段参数化为 \(\mathbf{u}(t) = \mathbf{a} + t (\mathbf{x} - \mathbf{a})\),我们对函数 \( g(t) = f(\mathbf{u}(t)) \) 应用一维版本的泰勒定理： \[ f(\mathbf{x}) = g(1) = g(0) + \sum_{j=1}^{k} \frac{1}{j!} g^{(j)}(0) + \int_0^1 \frac{(1 - t)^k}{k!} g^{(k+1)}(t) \, dt.~ \] 应用多元链式法则得到： \[ \begin{aligned} g^{(j)}(t) &= \frac{d^j}{dt^j} f(\mathbf{u}(t))\\ &= \frac{d^j}{dt^j} f(\mathbf{a} + t (\mathbf{x} - \mathbf{a})) \\ &= \sum_{|\alpha| = j} \binom{j}{\alpha} (D^\alpha f)(\mathbf{a} + t (\mathbf{x} - \mathbf{a})) (\mathbf{x} - \mathbf{a})^\alpha, \end{aligned}~ \] 其中 \( \binom{j}{\alpha} \) 是多项式系数。由于 \(\frac{1}{j!} \binom{j}{\alpha} = \frac{1}{\alpha!}\),我们得到： \[ f(\mathbf{x}) = f(\mathbf{a}) + \sum_{1 \leq |\alpha| \leq k} \frac{1}{\alpha!} (D^\alpha f)(\mathbf{a}) (\mathbf{x} - \mathbf{a})^\alpha + \sum_{|\alpha| = k+1} \frac{k+1}{\alpha!} (\mathbf{x} - \mathbf{a})^\alpha \int_0^1 (1 - t)^k (D^\alpha f)(\mathbf{a} + t (\mathbf{x} - \mathbf{a})) \, dt.~ \]

6. 另见

• 阿达玛引理
• Laurent 级数 – 含有负幂项的幂级数
• Padé 近似 – 用给定阶的有理函数对一个函数进行 “最优” 近似
• 牛顿级数 – 导数的离散类比
• 近似理论 – 研究如何通过不完全精确的数学计算得到可接受的近似值的理论
• 函数近似 – 用良好性质的函数来近似任意函数的方法

7. 脚注

1. (2013)。“线性与二次近似”，检索于 2018 年 12 月 6 日。
2. Taylor, Brook (1715)。*Methodus Incrementorum Directa et Inversa* [增量法的直接与反方法]（拉丁文），伦敦，第 21–23 页（命题 VII，定理 3，推论 2）。英文翻译见 Struik, D. J.（1969），《1200–1800 年数学文献选集》，马萨诸塞州剑桥：哈佛大学出版社，第 329–332 页。
3. Kline 1972，第 442 页、第 464 页。
4. Genocchi, Angelo；Peano, Giuseppe（1884），《微分计算与积分计算原理》，第 67 条，第 XVII–XIX 页，Fratelli Bocca 出版社。
5. Spivak, Michael（1994），《微积分》（第 3 版），德克萨斯州休斯敦：Publish or Perish 出版社，第 383 页，ISBN 978-0-914098-89-8。
6. “泰勒公式”，《数学百科全书》，EMS 出版社，2001 年（原 1994 年）。
7. 对于 \( f^{(k)} \) 在闭区间 [a, x] 上连续的假设不是多余的。尽管 \( f \) 在开区间 (a, x) 上具有 \( k+1 \) 次可导性意味着 \( f^{(k)} \) 在该开区间上连续，但并不意味着它在闭区间 [a, x] 上连续，也就是说不能保证其在区间端点处连续。例如，定义函数 \( f : [0,1] \to \mathbb{R} \)，在 \( (0,1] \) 上取 \( \sin\left(1/x\right) \)，并令 \( f(0) = 0 \)。这个函数在 0 处不连续，但在 \( (0,1) \) 上连续。此外可以证明它有一个反导函数，因此该反导函数在 \( (0,1) \) 上可导，其导数（即 \( f \)）在 \( (0,1) \) 上连续，但在闭区间 [0,1] 上不连续。因此该定理在此情况下不适用。
8. Kline 1998，第 20.3 节；Apostol 1967，第 7.7 节。
9. Apostol 1967，第 7.7 节。
10. Apostol 1967，第 7.5 节。
11. Apostol 1967，第 7.6 节。
12. Rudin 1987，第 10.26 节。
13. 这来自定理的反复应用：若函数 \( f \) 的偏导在 \( a \) 的某邻域内存在且在 \( a \) 处连续，则 \( f \) 在 \( a \) 处可微。参见例如 Apostol 1974，第 12.11 定理。
14. Königsberger，《分析 2》，第 64 页及后续。
15. Folland, G. B. “多元函数的高阶导数与泰勒公式”（PDF），华盛顿大学数学系，检索于 2024 年 2 月 21 日。
16. Stromberg 1981。
17. Hörmander 1976，第 12–13 页。

8. 参考文献

• Apostol, Tom（1967），《微积分》，Wiley 出版社，ISBN 0-471-00005-1。
• Apostol, Tom（1974），《数学分析》，Addison–Wesley 出版社。
• Bartle, Robert G.; Sherbert, Donald R.（2011），《实变分析导论》（第 4 版），Wiley 出版社，ISBN 978-0-471-43331-6。
• Hörmander, L.（1976），《线性偏微分算子，第 1 卷》，Springer 出版社，ISBN 978-3-540-00662-6。
• Kline, Morris（1972），《从古至今的数学思想》，第 2 卷，牛津大学出版社。
• Kline, Morris（1998），《微积分：直观与物理方法》，Dover 出版社，ISBN 0-486-40453-6。
• Pedrick, George（1994），《分析学初阶》，Springer 出版社，ISBN 0-387-94108-8。
• Stromberg, Karl（1981），《经典实变分析导论》，Wadsworth 出版社，ISBN 978-0-534-98012-2。
• Rudin, Walter（1987），《实变与复变分析》（第 3 版），McGraw-Hill 出版社，ISBN 0-07-054234-1。
• Tao, Terence（陶哲轩）（2014），《分析学，第 I 卷》（第 3 版），Hindustan Book Agency，ISBN 978-93-80250-64-9。

9. 外部链接

• [余弦函数的泰勒级数近似 - cut-the-knot 网站](http://www.cut-the-knot.org)
• [三角函数的泰勒展开交互演示小程序]
• [重新认识泰勒级数 - 全面数值方法研究所 (Holistic Numerical Methods Institute)]