指数函数（综述）

贡献者：待更新

　　本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　在数学中，指数函数是唯一一个将零映射为一且其导数在所有点上都等于自身的实函数。变量 $x$ 的指数函数记作 $\exp x$ 或 $e^x$，这两种记法可以互换使用。之所以称其为 “指数”，是因为其自变量可以看作是某个常数 $e \approx 2.718$（即底数）的幂指数。指数函数有多种定义方式，尽管它们的形式迥异，但在数学意义上是等价的。

　　指数函数可以将加法转化为乘法：它将加法的单位元 0 映射为乘法的单位元 1，并且满足加法转乘法的性质，即 $ \exp\left(x + y\right) = \exp x \cdot \exp y$。它的反函数是自然对数函数，记作 $\ln$ 或 $\log$，它则将乘法转化为加法：$ \ln\left(x \cdot y\right) = \ln x + \ln y$。

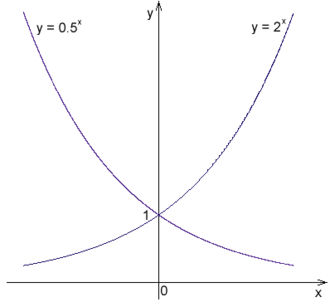
　　指数函数有时被称为自然指数函数，以对应自然对数的名称，用以区别于其他也常被称作 “指数函数” 的一些函数。这些函数包括形如 $f(x) = b^x$ 的函数，即以固定底数 $b$ 的幂函数。更一般地，尤其在实际应用中，形如 $f(x) = a b^x$ 的函数也被称为指数函数。这些函数被称为 “指数增长” 或 “指数衰减”，是因为当 $x$ 增加时，函数 $f(x)$ 的变化速率与它当前的取值成正比。

　　指数函数可以推广到接受复数作为自变量。这一推广揭示了复数乘法、复平面中的旋转以及三角函数之间的内在联系。欧拉公式 $ \exp\left(i\theta\right) = \cos\theta + i\sin\theta$ 正是这些关系的集中表达和总结。

　　指数函数甚至还可以进一步推广到其他类型的自变量，比如矩阵以及李代数中的元素。

1. 图像

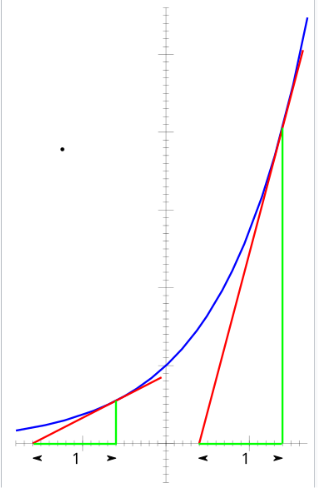
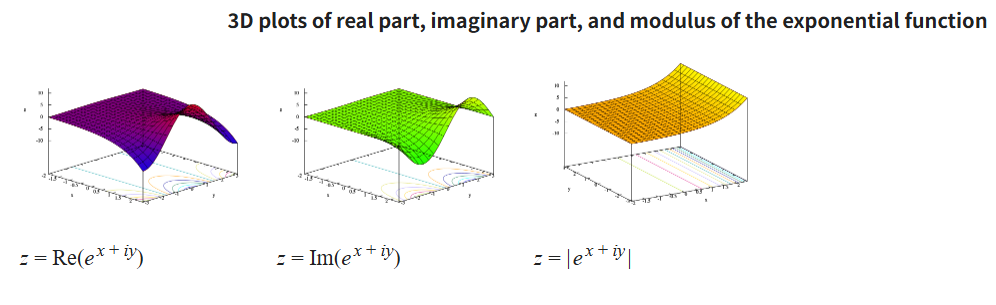
　　函数 $y = e^x$ 的图像是一个向上增长的曲线，并且其增长速度快于任何幂函数 $x^n$ 的增长速度。$^\text{[1]}$ 该图像始终位于 $x$ 轴之上，但在 $x$ 取非常大的负值时会无限接近于 $x$ 轴，因此 $x$ 轴是其一条水平渐近线。方程 $\frac{d}{dx}e^x = e^x$ 意味着该图像上任一点的切线斜率，等于该点的函数值（即该点的 $y$ 坐标）。

2. 定义与基本性质

　　指数函数有多种形式迥异但在数学上等价的定义方式。

微分方程

图 1：指数函数的导数等于其函数值。由于导数表示切线的斜率，这意味着图中的所有绿色直角三角形的底边长度为 1。

　　最简单的定义之一是：指数函数是唯一一个可导函数，其导数等于自身，并且在变量为 0 时取值为 1。

　　这个 “概念性” 定义需要证明存在性和唯一性，但它使得指数函数的主要性质可以很容易地推导出来。

　　唯一性：若 $f(x)$ 和 $g(x)$ 是两个满足上述定义的函数，那么根据商法则，函数 $f/g$ 的导数在所有点上都为零。这意味着 $f/g$ 是一个常数函数；又因为 $f(0) = g(0) = 1$，所以这个常数为 1，即 $f(x) = g(x)$。

　　存在性将在接下来的两个小节中分别加以证明。

自然对数的反函数

　　指数函数是自然对数函数的反函数。根据反函数定理，自然对数函数存在反函数，而这个反函数正好满足前述指数函数的定义，这构成了指数函数存在性的第一种证明方式。因此，有如下恒等式： $$ \ln\left(\exp x\right) = x \\ \exp\left(\ln y\right) = y~ $$ 对所有实数 $x$ 和所有正实数 $y$ 都成立。

幂级数

　　指数函数可以表示为以下幂级数的和：$^\text{[2][3]}$ $$ \exp\left(x\right) = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots = \sum_{n=0}^{\infty} \frac{x^n}{n!}~ $$

图 2：指数函数（蓝色曲线）及其幂级数前 $n + 1$ 项的部分和（红色曲线）

　　其中 $n!$ 表示 $n$ 的阶乘（即前 $n$ 个正整数的乘积）。根据比值判别法，该级数在任意 $x$ 上都绝对收敛。因此，可以逐项求导，从而得出该级数的和满足之前给出的指数函数定义。

　　这就构成了指数函数存在性的第二种证明，并且作为推论，还说明了指数函数在任意 $x$ 上都有定义，且在每一点都等于其 Maclaurin 级数的和。

函数方程

　　指数函数满足如下函数方程： $$ \exp\left(x + y\right) = \exp\left(x\right) \cdot \exp\left(y\right) ~ $$ 这个结论源于指数函数的唯一性，以及函数 $f(x) = \exp\left(x + y\right) / \exp\left(y\right) $ 也满足前面提到的指数函数定义。

　　可以证明，任何满足该函数方程的函数，如果它是连续的或单调的，则一定具有如下形式：$x \mapsto \exp\left(c x\right) $ 其中 $c$ 为常数。这样的函数必然是可导的，并且当其在 0 处的导数为 1 时，就与标准的指数函数相等。

整数幂的极限

　　指数函数可以表示为当整数 $n \to \infty$ 时的极限：$^\text{[4][3]}$ $$ \exp\left(x\right) = \lim_{n \to +\infty} \left(1 + \frac{x}{n}\right)^n~ $$ 利用对数函数的连续性，可以通过取对数来证明这一点，方法是证明： $$ x = \lim_{n \to \infty} \ln\left( \left(1 + \frac{x}{n} \right)^n \right) = \lim_{n \to \infty} n \ln\left(1 + \frac{x}{n} \right)~ $$ 例如可以通过泰勒定理来证明该极限关系。

性质

　　倒数：由函数方程可得 $e^x \cdot e^{-x} = 1$ 因此，对任意实数 $x$，都有 e^x \neq 0,$$\frac{1}{e^x} = e^{-x}~$$正值性：对所有实数 $x$，都有 $e^x > 0$ 这一点可以由介值定理推出。由于 $e^0 = 1$，如果存在某个 $x$ 满足 $e^x < 0$，那么在区间 $[0, x]$ 上将存在某个点 $y$ 使得 $e^y = 0$。但因为指数函数恒等于其导数，它是严格单调递增的，不可能在某一点取得零值，从而得出矛盾，因此 $e^x$ 必为正值。

　　将幂运算扩展到任意正实数底数：设 $b$ 为一个正实数。由于指数函数与自然对数互为反函数，有 $b = \exp\left(\ln b\right) $ 若 $n$ 是整数，由对数的函数方程可得： $$ b^n = \exp\left(\ln b^n\right) = \exp\left(n \ln b\right) ~ $$ 由于最右边的表达式在 $n$ 为任意实数时都有定义，这就允许我们对任意正实数 $b$ 和任意实数 $x$ 定义 $$ b^x = \exp\left(x \ln b\right) ~ $$ 特别地，当底数 $b$ 取自然常数 $e = \exp\left(1\right) $ 时，有 $\ln e = 1$ 因此 $$ e^x = \exp\left(x\right) ~ $$ 这说明 $e^x$ 与 $ \exp\left(x\right) $ 这两种指数函数的记法是等价的。

3. 一般指数函数

　　一个函数若具有如下形式 $x \mapsto b^x$ 即通过固定底数 $b$，让指数 $x$ 变化而得到的函数，通常被称为一个指数函数（注意使用不定冠词 “an exponential function”）。

　　更一般地，特别是在应用场景中，“指数函数” 一词通常指形如 $f(x) = a b^x$ 的函数。这样定义的合理性在于：如果函数的取值代表某种物理量，那么单位的变更会改变常数 $a$ 的数值，因此强行规定 $a = 1$ 是不合理的。

　　这些最一般形式的指数函数是满足以下等价刻画的可导函数：

存在常数 $a$ 和 $b > 0$，使得对任意 $x$ 有：$f(x) = a b^x$
存在常数 $a$ 和 $k$，使得对任意 $x$ 有：$f(x) = a e^{k x}$
函数导数与自身之比 $f'(x)/f(x)$ 与 $x$ 无关，即该比值是一个常数。
对于任意实数 $d$，比值 $f(x + d)/f(x)$ 与 $x$ 无关；也就是说，对所有 $x, y^\text{[5]}$ 都有： $$ \frac{f(x + d)}{f(x)} = \frac{f(y + d)}{f(y)}~ $$

图 3：以底数 2 和 $1/2$ 的指数函数

　　指数函数的底数，是将其写成形式 $x \to a b^x$ 时幂运算中的底数，即 $b$。$^\text{[6]}$ 在其他几种刻画中，底数分别为：第二种形式中的底数为 $e^k$；第三种刻画中为 $\exp\left( \frac{f'(x)}{f(x)} \right) $；最后一种刻画中为 $\left( \frac{f(x+d)}{f(x)} \right)^{1/d}$。

在实际应用中

　　最后一种刻画方式在经验科学中非常重要，因为它可以直接通过实验检验一个函数是否为指数函数。

　　所谓的指数增长或指数衰减，即变量的变化速率与变量的当前值成正比，通常使用指数函数建模。例如：无限制的人口增长可能导致马尔萨斯灾难、连续复利计算、放射性衰变等现象。

　　若用于建模的函数具有如下形式 $x \mapsto a e^{kx}$ 或者等价地，是微分方程 $y' = k y$ 的解，那么常数 $k$ 会根据具体语境被称为衰减常数、崩解常数 $^\text{[7]}$、速率常数 $^\text{[8]}$，或转化常数 $^\text{[9]}$。

等价性的证明

　　为了证明上述各性质之间的等价性，可以按如下方式进行：

　　前两种刻画是等价的，因为如果 $b = e^k \quad \text{且} \quad k = \ln b$ 那么就有 $$ e^{k x} = (e^k)^x = b^x~ $$ 因此，形式 $a b^x$ 与 $a e^{k x}$ 是完全等价的。

　　而指数函数的基本性质（即导数等于自身、以及满足函数方程）则直接推出第三种和最后一种刻画。

　　假设第三个条件成立，令 $k = \frac{f'(x)}{f(x)}$ 为一个常数。由于 $\frac{\partial}{\partial x} e^{k x} = k e^{k x}$ 根据求导的商法则，有 $$ \frac{\partial}{\partial x} \left( \frac{f(x)}{e^{k x}} \right) = 0~ $$ 因此存在某个常数 $a$，使得 $f(x) = a e^{k x}$

　　如果最后一个条件成立，令 $\varphi(d) = f(x + d)/f(x)$ 该表达式与 $x$ 无关。由于 $\varphi(0) = 1$ 我们可以写成： $$ \frac{f(x + d) - f(x)}{d} = f(x)\frac{\varphi(d) - \varphi(0)}{d}~ $$ 当 $d \to 0$ 时，右边趋于 $f(x) \cdot \varphi'(0)$ 因此导数存在，且 $\frac{f'(x)}{f(x)} = \varphi'(0) = k$ 这就验证了第三个条件，且得出 $f(x) = a e^{k x}$ 对于某个常数 $a$，并且 $\varphi(d) = e^{k d}$ 进一步推导可得： $$ \left( \frac{f(x + d)}{f(x)} \right)^{1/d} = e^k~ $$ 此表达式不依赖于 $x$ 和 $d$。

4. 复利

　　指数函数最早出现在雅各布·伯努利 1683 年对复利的研究中。$^\text{[10]}$ 正是在这项研究中，伯努利引入了如下极限表达式： $$ \lim_{n \to \infty} \left(1 + \frac{1}{n}\right)^n~ $$ 这一极限数后来被称为欧拉常数，记作 $e$。

　　在计算连续复利时，指数函数如下地参与其中。

　　如果本金为 1，年利率为 $x$，且按每月复利计算，则每月所获利息为当前金额的 $\frac{x}{12}$，因此每月总金额都会乘以 $(1 + \frac{x}{12})$，一年结束时的总金额为 $(1 + \frac{x}{12})^{12}$ 如果改为按日复利，则总金额为 $(1 + \frac{x}{365})^{365}$ 当一年中的计息周期数趋于无限多时，就得到指数函数的极限定义： $$ \exp x = \lim_{n \to \infty} \left(1 + \frac{x}{n} \right)^n~ $$ 该极限表达式最早由莱昂哈德·欧拉给出。$^\text{[4]}$

5. 微分方程

　　指数函数在微分方程的解中非常常见。

　　事实上，指数函数本身可以定义为某些微分方程的解。最简单的例子是，它是以下最基本微分方程的解：$y' = y$ 而所有其他形如 $y = a b^x$ 的指数函数，都是微分方程 $y' = k y$ 的解；反过来，该微分方程的所有解都具有这种形式。

　　对于更一般的微分方程，如 $$ y' + k y = f(x)~ $$ 其解会以更复杂的方式涉及指数函数，通解为： $$ y = c e^{-k x} + e^{-k x} \int f(x) e^{k x}dx~ $$ 其中 $c$ 是任意常数，积分表示被积函数的一个原函数（不定积分）。

　　更广义地，任何具有常系数的线性微分方程的解都可以用指数函数以及（在非齐次情形下）不定积分来表示。这一点对于常系数线性微分方程组也同样成立。

6. 复指数函数

图 4：复指数函数 $e^z$ 在复平面上从 $-2 - 2i$ 到 $2 + 2i$ 的图像

　　指数函数可以自然地扩展为一个复函数，即定义域与取值域都是复数的函数，其在实数上的限制就是先前定义的指数函数，下面将其称为实指数函数。这个扩展后的函数也被称为指数函数，记作 $e^z$ 或 $ \exp\left(z\right) $。为了区分实数情形与复数情形，该扩展函数也称为复指数函数，或简称为复指数。

　　大多数关于实指数函数的定义都可以直接照搬用于定义复指数函数，而它们等价性的证明在复数情形下与实数情形完全相同。

　　复指数函数可以通过多种彼此等价的方式来定义，这些方式与实数情况下所用的方法是相同的。

图 5

　　复指数函数是唯一一个满足以下条件的复函数：它等于其复导数，并且在自变量为 $0$ 时取值为 $1$： $$ \frac{d e^z}{dz} = e^z \quad \text{且} \quad e^0 = 1~ $$ 复指数函数可以表示为级数 $$ e^z = \sum_{k=0}^{\infty} \frac{z^k}{k!}~ $$ 该级数在所有复数 $z$ 上都绝对收敛，因此复指数函数是一个整函数（即在整个复平面上解析的函数）。

　　复指数函数也可以表示为以下极限形式： $$ e^z = \lim_{n \to \infty} \left(1 + \frac{z}{n} \right)^n~ $$ 复指数函数满足如下函数方程： $$ e^{w + z} = e^w \cdot e^z~ $$ 对任意复数 $w$ 和 $z$ 都成立。复指数函数是唯一一个连续函数，它满足上述函数方程，并且在 $z = 0$ 时取值为 1。

　　复对数函数是复指数函数的右逆函数： $$ e^{\log z} = z~ $$ 然而，由于复对数函数是一个多值函数，因此有： $$ \log e^z = \{ z + 2ik\pi \mid k \in \mathbb{Z} \}~ $$ 这使得从复对数定义复指数函数变得困难。反之，复对数函数通常是通过复指数函数来定义的。

　　复指数函数具有以下性质：

　　倒数关系： $$ \frac{1}{e^z} = e^{-z}~ $$ 并且对任意复数 $z \in \mathbb{C}$，有 $e^z \neq 0$

　　它是一个周期函数，周期为 $2i\pi$，即： $$ e^{z + 2ik\pi} = e^z \quad \text{对任意} \; k \in \mathbb{Z}~ $$ 这一性质源于欧拉恒等式 $e^{i\pi} = -1$ 以及指数函数的函数恒等式。

　　共轭性质：复指数的共轭等于共轭后的指数函数： $$ \overline{e^z} = e^{\overline{z}}~ $$ 模长性质：复指数的模为其实部的指数： $$ |e^z| = e^{| \operatorname{Re} (z)|}~ $$ 其中 $ \operatorname{Re} (z)$ 表示复数 $z$ 的实部。

与三角函数的关系

　　复指数函数与三角函数之间存在密切联系，通过欧拉公式表达如下： $$ e^{it} = \cos\left(t\right) + i \sin\left(t\right) ~ $$ 这个公式将复指数函数分解为实部和虚部，从而得到： $$ e^{x + i y} = e^x \cos y + i e^x \sin y~ $$ 三角函数可以反过来用复指数函数表示： $$ \begin{aligned} \cos x &= \frac{e^{ix} + e^{-ix}}{2} \\ \sin x &= \frac{e^{ix} - e^{-ix}}{2i} \\ \tan x &= i\,\frac{1 - e^{2ix}}{1 + e^{2ix}} \end{aligned}~ $$ 在这些公式中，变量 $x, y, t$ 通常被视为实变量，但这些等式在将变量视为复变量时同样成立。这些公式也可以用来定义复变量的三角函数。$^\text{[11]}$

图像

图 6

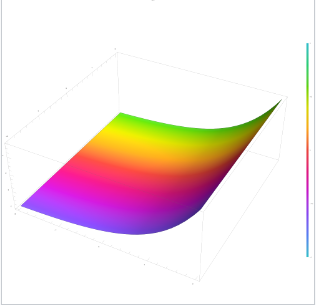
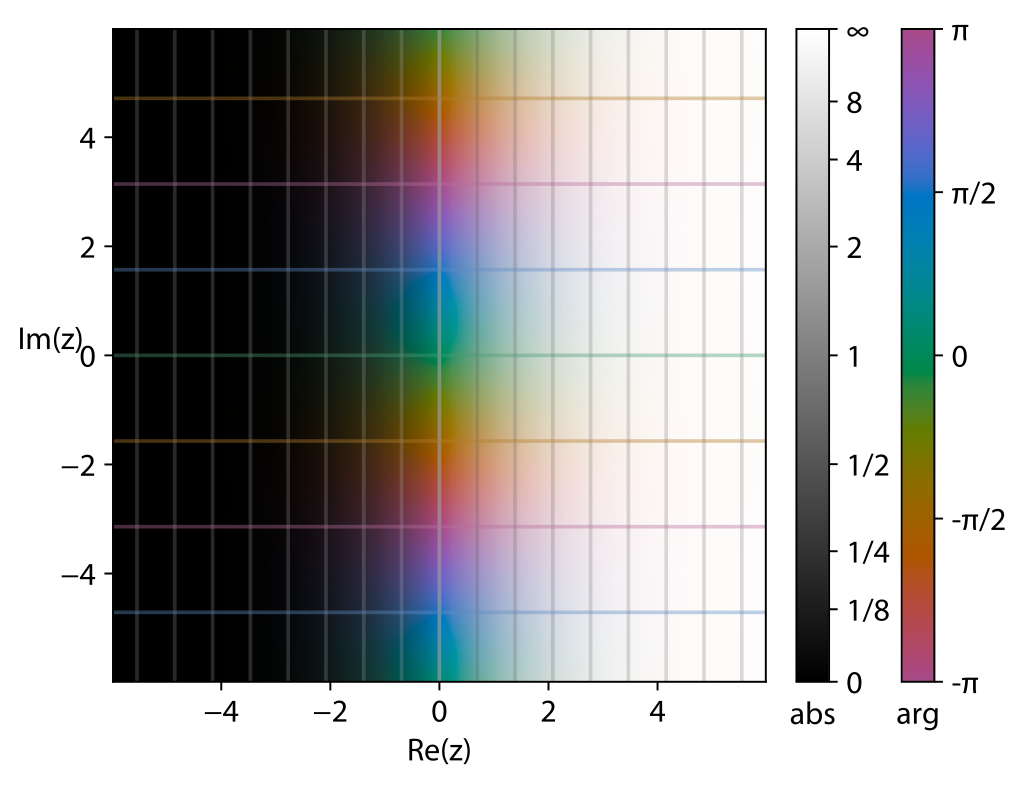
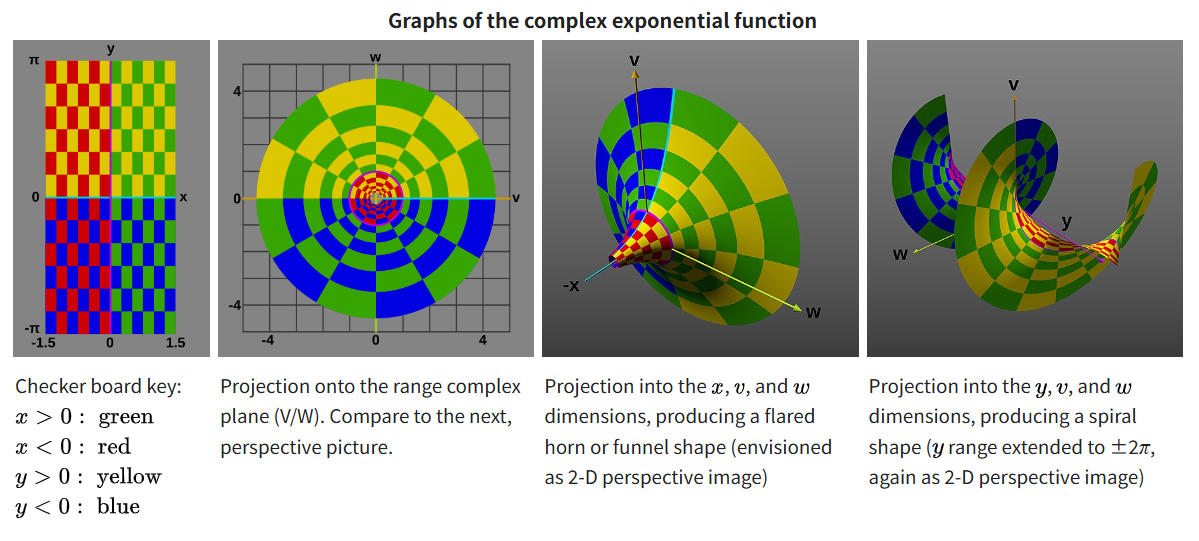
　　将复指数函数视为一个涉及四个实变量的函数： $$ v + iw = \exp\left(x + iy\right) ~ $$ 那么其图像就是一个在四维空间中弯曲的二维曲面。

　　从以颜色编码的 $xy$ 平面上的一部分区域出发，接下来的图像是该图形在二维或三维空间中的不同投影表示。

图 7

　　第二张图展示了复指数函数如何将定义域中的复平面映射到值域中的复平面：

原点（零）被映射到 1
实轴（$x$ 轴）被映射到正实轴（$v$ 轴）
虚轴（$y$ 轴）以恒定的角速度绕着单位圆展开
实部为负的点被映射到单位圆内部
实部为正的点被映射到单位圆外部
实部为常数的点被映射为以原点为中心的圆
虚部为常数的点被映射为从原点射出的射线

　　第三张与第四张图展示了第二张图中未显示的其他两个维度上的图像是如何延展的。

　　第三张图展示了图像沿实轴 $x$ 的延展情况：它表明整个图像是实指数函数图像绕 $x$ 轴旋转所形成的一个旋转曲面，形状类似于一个喇叭或漏斗。

　　第四张图展示了图像沿虚轴 $y$ 的延展情况：它表明当 $y$ 为正和负时，图像的表面不会在负实轴 $v$ 上真正相交，而是围绕 $y$ 轴形成一个螺旋曲面。由于图像中的 $y$ 值被扩展到了 $\pm 2\pi$，这张图也更清晰地表现了在虚部方向上以 $2\pi$ 为周期的特性。

7. 矩阵与巴拿赫代数

　　指数函数的幂级数定义同样适用于方阵（在这种情形下称为矩阵指数函数），以及更一般的情形——任意带单位元的巴拿赫代数 $B$。在这种设置下，有：$e^0 = 1$ 对于任意 $x \in B$，$e^x$ 是可逆的，其逆为 $e^{-x}$ 如果 $x$ 与 $y$ 可交换（即 $xy = yx$），则有恒等式：$e^{x + y} = e^x e^y$ 但若 $x$ 与 $y$ 不交换，此等式则不一定成立。

　　一些其他定义方式也可以导出同样的函数。例如，可以定义： $$ e^x = \lim_{n \to \infty} \left(1 + \frac{x}{n} \right)^n~ $$ 或者也可以定义为 $f_x(1)$，其中 $f_x: \mathbf{R} \to B$ 是下列微分方程的解：$\frac{d f_x}{dt}(t) = x f_x(t), \quad f_x(0) = 1$ 由此可得，对于任意 $t \in \mathbf{R}$，都有 $f_x(t) = e^{tx}$

8. 李代数

　　给定一个李群 $G$ 及其对应的李代数 $\mathfrak{g}$，可以定义一个从李代数到李群的指数映射 $\mathfrak{g} \mapsto G$，它满足与前述指数函数相似的性质。

　　事实上，由于实数域 $\mathbf{R}$ 是在乘法下的正实数李群的李代数，因此普通的实数指数函数其实是李代数情形的一个特例。同样地，李群 $\mathrm{GL}(n, \mathbf{R})$（即所有可逆 $n \times n$ 实矩阵的群）对应的李代数是 $\mathrm{M}(n, \mathbf{R})$（即所有 $n \times n$ 实矩阵的空间），因此矩阵指数函数也是李代数指数映射的一个特例。

　　需要注意的是，恒等式 $ \exp\left(x + y\right) = \exp\left(x\right) \exp\left(y\right) $ 在 $x$ 与 $y$ 不对易的情况下会失效；此时需要使用 Baker–Campbell–Hausdorff 公式来引入相应的修正项。

9. 超越性

　　函数 $e^z$ 是一个超越函数，这意味着它不是有理函数域 $\mathbb{C}(z)$ 上某个多项式的根。

　　更具体地说，如果 $a_1, \ldots, a_n$ 是互不相同的复数，那么函数 $e^{a_1 z}, \ldots, e^{a_n z}$ 在 $\mathbb{C}(z)$ 上是线性无关的，因此 $e^z$ 是 $\mathbb{C}(z)$ 上的超越元素。

10. 计算

　　上述的泰勒级数定义在计算 $e^x$（或其近似值）时通常是高效的。然而，当自变量接近 $x = 0$ 时，结果会非常接近于 1，此时若使用浮点数运算来计算差值 $e^x - 1$，可能会导致有效数字的大量甚至全部丢失，从而产生较大的相对误差，甚至得出毫无意义的结果。

　　根据威廉·卡恩的建议，为了避免上述问题，设计一个专门计算 $e^x - 1$ 的函数是有用的，这种函数通常被称为 `expm1`，它通过绕过 $e^x$ 的直接计算来提高精度。

　　例如，可以使用如下泰勒级数展开来计算： $$ e^x - 1 = x + \frac{x^2}{2} + \frac{x^3}{6} + \cdots + \frac{x^n}{n!} + \cdots~ $$ 这个函数最早于 1979 年被实现于惠普 HP-41C 计算器中，并被多个计算器系统 $^\text{[12][13]}$、操作系统（例如 Berkeley UNIX 4.3BSD$^\text{[14]}$）、计算机代数系统，以及编程语言（例如 C99$^\text{[15]}$）所提供。

　　除了以 $e$ 为底的指数函数外，IEEE 754-2008 标准还定义了在 $x$ 接近 0 时的其他底数的类似指数函数，如：$2^x - 1$（以 2 为底）$10^x - 1$（以 10 为底）

　　对于对数函数，也有类似的方法，详见 `log1p`（用于计算 $ \log\left(1 + x\right) $ 以避免精度损失）。

　　另有一个涉及双曲正切函数的恒等式： $$ \operatorname{expm1}(x) = e^x - 1 = \frac{2 \tanh\left(x/2\right) }{1 - \tanh\left(x/2\right) }~ $$ 该公式可在系统不支持 `expm1(x)` 时，提供对小 $x$ 的高精度计算结果。

连分数

　　指数函数也可以通过连分数进行计算。

　　一个用于计算 $e^x$ 的连分数可由欧拉恒等式导出如下： $$ e^x = 1 + \cfrac{x}{1 - \cfrac{x}{x + 2 - \cfrac{2x}{x + 3 - \cfrac{3x}{x + 4 - \ddots}}}}~ $$ 以下这个广义连分数用于计算 $e^z$，收敛速度更快：$^\text{[16]}$ $$ e^{z} = 1 + \cfrac{2z}{2 - z + \cfrac{z^2}{6 + \cfrac{z^2}{10 + \cfrac{z^2}{14 + \ddots}}}}~ $$ 或者，通过代入 $z = \frac{x}{y}$，可得： $$ e^{\frac{x}{y}} = 1 + \cfrac{2x}{2y - x + \cfrac{x^2}{6y + \cfrac{x^2}{10y + \cfrac{x^2}{14y + \ddots}}}}~ $$ 当 $z = 2$ 时，有一个特殊的情形： $$ e^2 = 1 + \cfrac{4}{0 + \cfrac{2^2}{6 + \cfrac{2^2}{10 + \cfrac{2^2}{14 + \ddots}}}} = 7 + \cfrac{2}{5 + \cfrac{1}{7 + \cfrac{1}{9 + \cfrac{1}{11 + \ddots}}}}~ $$ 该公式在 $z > 2$ 的情况下仍然收敛，但收敛速度较慢。例如： $$ e^3 = 1 + \cfrac{6}{-1 + \cfrac{3^2}{6 + \cfrac{3^2}{10 + \cfrac{3^2}{14 + \ddots}}}} = 13 + \cfrac{54}{7 + \cfrac{9}{14 + \cfrac{9}{18 + \cfrac{9}{22 + \ddots}}}}~ $$

11. 参见

Carlitz 指数函数：特征为 $p$ 的指数函数类比
双重指数函数：指数函数的指数函数
指数域：带有额外运算的数学域
高斯函数
半指数函数：指数函数的复合平方根
Lambert W 函数#解指数方程：一种多值函数，用于解指数方程
指数相关主题列表
指数函数的不定积分列表
Mittag-Leffler 函数**：指数函数的一种推广
$p$-进指数函数
指数函数的 Padé 表（Padé table for exponential function）：用多项式分式逼近指数函数
相位因子

12. 注释

参考文献

“Exponential Function Reference.” [www.mathsisfun.com](https://www.mathsisfun.com)。访问日期：2020-08-28。
Rudin, Walter（1987 年）。《实变与复变分析》（第 3 版）。纽约：McGraw-Hill，第 1 页。ISBN 978-0-07-054234-1。
Weisstein, Eric W. “Exponential Function.” [mathworld.wolfram.com](https://mathworld.wolfram.com)。访问日期：2020-08-28。
Maor, Eli. *e: the Story of a Number*，第 156 页。
G. Harnett，《微积分 1》，1998 年，章节 “函数续讲”： “一般的指数函数具有这样的性质：两个输出值之比仅取决于输入值之差。当输入变化一个单位时，输出值之比即为底数。”
G. Harnett，《微积分 1》，1998 年；章节 “函数续讲 / 指数与对数” 中写道： “当输入变化一个单位时，输出值之比就是一般指数函数的底数。”
Serway, Raymond A.；Moses, Clement J.；Moyer, Curt A.（1989）。《现代物理学》（*Modern Physics*）。沃斯堡：Harcourt Brace Jovanovich，第 384 页。ISBN 0-03-004844-3。
Simmons, George F.（1972）。《微分方程及其应用与史料注释》）。纽约：McGraw-Hill，第 15 页。LCCN 75173716。
《麦格劳-希尔科学与技术百科全书》（第 10 版）。纽约：McGraw-Hill，2007 年。ISBN 978-0-07-144143-8。
O'Connor, John J.；Robertson, Edmund F.，“Exponential function”，载于英国圣安德鲁斯大学 *MacTutor 数学史档案馆*。
Apostol, Tom M.（1974）。《数学分析》（第 2 版）。马萨诸塞州雷丁：Addison Wesley，第 19 页。ISBN 978-0-201-00288-1。
《HP 48G 系列图形计算器——高级用户参考手册（AUR）》（第 4 版）。惠普公司。1994 年 12 月［1993 年］出版。编号：HP 00048-90136，ISBN 0-88698-01574-2。访问日期：2015-09-06。
《HP 50g / 49g+ / 48gII 图形计算器高级用户参考手册（AUR）》（第 2 版）。惠普公司。2009 年 7 月 14 日［2005 年］出版。编号：HP F2228-90010。访问日期：2015-10-10。［参考链接见文中］
Beebe, Nelson H. F.（2017-08-22）。“第 10.2 章：接近零点的指数函数”。载于《数学函数计算手册：使用 MathCW 便携软件库编程》（第 1 版）。美国犹他州盐湖城：Springer International Publishing AG，第 273–282 页。 DOI: 10.1007/978-3-319-64110-2 ISBN: 978-3-319-64109-6 LCCN: 2017947446 S2CID: 30244721 ——Berkeley UNIX 4.3BSD 于 1987 年首次引入了 `expm1()` 函数。
Beebe, Nelson H. F.（2002-07-09）。“`expm1 = exp(x) − 1` 的计算方法”（PDF 文件）。版本 1.00。美国犹他州盐湖城：犹他大学数学系，科学计算中心。访问日期：2015-11-02。
Lorentzen, L.；Waadeland, H.（2008）。“A.2.2 指数函数”。载于《连分数》（*Continued Fractions*），Atlantis 数学研究系列，第 1 卷，第 268 页。 DOI: 10.2991/978-94-91216-37-4 ISBN: 978-94-91216-37-4

13. 外部链接

“Exponential function”，《数学百科全书》，EMS Press，2001 年 [原始出版于 1994 年]

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。