复旦大学 2015 年考研普通物理

贡献者： _Eden_

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

　　 1. 图示系统处于同一铅垂平面内，细长直杆 $A B$ 的长度为 $r$, 以匀角速度 $\omega$ 绕轴 $A$ 作顺时针转动，通过其 $B$ 端与半径为 $R=2 r$ 的扇形板 $D G H$ 的圆弧边缘 $(D$ 为其圆心）接触，从而带动扇形板绕轴 $O$ 转动，且 $O D=\sqrt{3} R / 3$, 试求图示瞬时（$A B$ 处于水平位置，$D G$ 处于铅垂位置) 扇形板的角速度和角加速度。(25 分)

　　 2. 真空中，有一平行板电容器，两块极板均为半径为 $a$ 的圆板，将它连接到一个交变电源上，使极板上的电荷按规律 $Q=Q_{0} \sin \omega t$ 随时间 $t$ 变化（式中 $Q_{0}$ 和 $\omega$ 均为常量 $)$。在略去边缘效应的条件下，试求两极板间任一点的磁场强度 $ \boldsymbol{\mathbf{H}} $。(15 分)

　　 3. 如图所示，细圆环管在相连部件带动下沿水平直线轨道纯滚动，管内有一壁虎，相对于环管爬行，壁虎可被视为一点，在图中以小球 $B$ 代替。图示瞬间，壁虎与环管的中心处于同一水平线上，壁虎相对环管的速率为 $u$, 相对速度的方向朝下，相对速度大小的改变率等于 $0$, 环管中心 $O$ 点的速度向右，速度大小也为 $u$, 加速度为 $0$。环管的中心半径等于 $R$。求在此瞬时： (15 分)

　　 (1)壁虎相对地面的速度大小;

　　 (2)壁虎相对地面的加速度大小;

　　 (3)壁虎在相对地面的运动轨迹上所处位置点的曲率半径的大小。

　　 4. 用钠光 $(\lambda=589.3 \mathrm{~nm})$ 观察迈克尔逊干涉条纹。由于观察屏的大小限制，屏上只能看到有限个亮环。设开始时屏上有 $6$ 个亮环，中心是亮的。移动平面镜 $R$ 后，看到中心冒出了 $8$ 个亮环，此时观察屏上共有 $10$ 个亮环，中心也是亮的。求：(15 分)

　　 (1) $M_{1}$ 移动的距离：

　　 (2) $M_{1}$ 移动时，$M_{1}$ 和平面镜 $M_{2}$ 的虚像 $M_{2}^{\prime}$ 之间的等效空气膜是变薄，还是变厚？

　　 (3) 移动 $M_{1}$ 后，等效空气膜的厚度。

　　 5. 一平行板电容器的电容为 $100 p F$, 极板的面积为 $100 \mathrm{~cm}^{2}$, 极板间充满相对介电常数为 $5.4$ 的云母电介质，真空介电常数为 $8.85 \times 10^{-12}(F / m)$, 试求极板上电势差为 $50 V$ 时，(20 分)

　　 (1)云母中的电场强度 $E$;

　　 (2)电容器极板上的自由电荷;

　　 (3)云母介质面上的极化面电荷。

　　 6. 质量为 $m$、半径为 $r$ 的均质球置于水平桌面上，受一水平方向的冲击力作用，力的作用线通过球心，力的冲量为 $J$, 试求：(20 分)

　　 (1)求冲击刚结束时球心的速度 $v_{0}$;

　　 (2)由于受到䍒面摩擦力的作用，球最终将在桌面上作纯滚动，求这时球的角速度 $\omega$;

　　 (3) 求球与桌面间摩擦所消耗的能量。(已知均质球对过球心转轴的转动惯量为 $\left.\frac{2}{5} m r^{2}\right)$

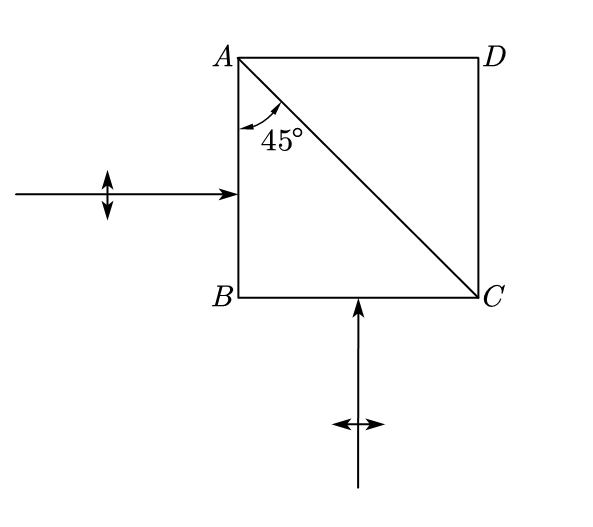
　　 7. 如图所示为一个方解石直角棱镜（左端）和一个普通光学玻璃棱镜（右端）组成的双折射分束棱镜，两棱镜的锐角均为 $45^{\circ}$, 光胶而成，方解石棱镜的光轴方向如图所示。已知方解石 $n_{o}=1.6584, n_{e}=1.4864$, 玻璃棱镜折射率 $n=1.54$。(20 分)

　　 (1) 分别画出自然光沿垂直于 $A B$ 面和沿垂直于 $B C$ 面的方向入射时，从棱镜出射的光束方向。说明出射光的偏振态，标出各光束的振动方向。

　　 (2) 对于自然光垂直于 $A B$ 面入射的情形，计算两束出射光之间的夹角。

　　 8. 试证明：刚性绝热容器的放气过程中容器内理想气体的状态参数服从 $T p^{-\frac{k-1}{k}}=$ 常数

　　 9. 一个焦距为 $60 \mathrm{~mm}$, 相对孔径为 $1: 2$ 的投影物镜，将物平面放大 $6$ 倍投影在 屏幕上，如果屏幕上允许的几何弥散斑直径为 $0.3 \mathrm{~mm}$, 求基准物面前后的几何景深。 （20 分）

　　 10. 相同形状、相同体积的导体和绝缘体均匀电介质，分别放入静电场中，在 达到静电平衔以后。试回答 (20 分) （1）两种情况下，电场变化的主要不同之处： (2) 当电介质的介电常数 $\epsilon$ 趂向无限大时，两种情况下电场变化的结果会相同吗？为什么？

　　 11. 一个无限长的直圆柱导体，内有一无限长的直圆柱空洞，空洞的轴线与圆 柱体的轴线平行但不重合，相距为 $d$. 如果有电流密度为 $ \boldsymbol{\mathbf{j}} $ 的均匀电流沿导体的轴线方向流动，计算空洞内的磁感应强度。（20 分）

　　 12. 有一线度非常小的磁偶极子，它具有指向 $x$ 方向的固有磁矩 $ \boldsymbol{\mathbf{m}} $, 并正以速率 $v$ 沿 $x$ 轴运动。另有一半径为 $a$, 电阻为 $R$ 的细导线圆环，固定在垂直于 $x$ 轴的平面上，圆心位于距磁偶极子距离为 $r$ 的 $x$ 轴上。试求此时磁偶极子受到的阻力。假设 $v \ll c, a \ll r$, 导线环的自感和磁偶极子磁矩的变化可忽略。(20 分)