四川大学 2006 年硕士物理考试试题（933）

贡献者： 待更新

　　 声明：“该内容来源于网络公开资料，不保证真实性，如有侵权请联系管理员”

1. 简答题

1. 将一个带电 $+q$、半径为 $R$ 的大导体球 $B$ 移近一个半径为 $r$ 而不带电的小导体球 $A$,试判断下列说法是否正确？并说明理由。
   (1)$B$ 球电势高于 $A$ 球。
   (2)以无限远为电势零点，$A$ 球的电势小于 0。
   (3)在 $B$ 球表面附近任一点的场强等于 $\displaystyle \frac{q}{4\pi R^2}$
2. 指出下列有关电场强度与电势 $U$ 的关系的说法是否正确?并简要说明原因。
   (1)已知某点的就可以确定该点的 $U$。
   (2)已知某点的 $U$ 就可以确定该点的 $\vec E$。
   (3)$\vec E$ 不变的空间，$U$ 也一定不变。
   (4)$U$ 值相等的曲面上，$\vec E$ 值不一定相等。
3. 一根通有 $20A $ 电流的无限长细直导线，放在磁感应强度为 $B=10^{-3}T$ 的均匀外磁场中，导线与外磁场正交。试确定磁感应强度为零的各点的位置。

2. 应用题

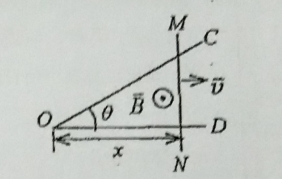
1. 如图 1 所示，有一弯成 $\theta$ 角的金属架 COD 放在磁场中，磁感强度 $\vec B$ 的方向垂直于金属架 COD 所在平面。一导体杆 MN 垂直于 OD 边，并在金属架上以恒定速度 $\bar v$ 向右滑动，$\bar v$ 与 MN 垂直.设 $t=0$ 时，$x=0$.分别求下列两种情形下，框架内的感应电动势 $E_i$:
   (1)磁场分布均匀，且 $\vec B$ 不随时间改变。
   
   
   图 1
   (2)磁场随时间和空间都变化，且磁场强度 $B=Kx\sin \omega t$。
2. (凝聚杰物理、光学、生物医学物理、应用电子技术专业考生必作)
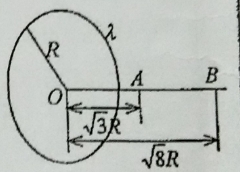
   如图 2 所示，一半径为 $R$ 的均匀带正电圆环，其电荷线密度为 $\lambda$。在其轴线上有 A、B 两点，它们与环心的距离分别为 $\displaystyle \bar{OA}=\sqrt{3}R,\bar{OB}=\sqrt{8}R$，一质量为 $m$、电荷为 $q$ 的粒子从 A 点运动到 B 点，求在此过程中电场力所作的功。
   
   图 2
3. (凝聚态物理、光学、生物医学物理、应用电子技术专业考生必作)
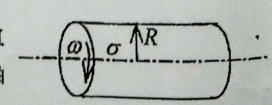
   如图 3 所示，一半径为 $R$ 的均匀带电无限长直圆筒，面电荷密度为 $\sigma$.该筒以角速度 $\omega$ 绕其轴线匀速旋转。试求圆筒内部的磁感强度。
   
   图 3
4. (通论物理、粒子物理与原子核物理、原子分子物理专业必作)
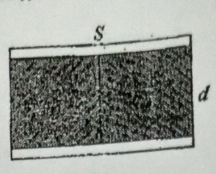
   如图 4 所示，一平行板电容器，极板面积为 $S$，两板间距离为 $d$，其中充有两种各向同性均匀电介质，相对介电常量分别为 $\varepsilon_{r1}$ 和 $\varepsilon_{r2}$，且各占一半体积。试证该电容器的电容为
   \begin{equation} C=\frac{s_0S}{2d}(\varepsilon_{r1}+\varepsilon_{r2})~ \end{equation}
   并说明该电容器相当于左、右两部分作为单独的电容器的并联。
   
   图 4
5. (理论物理、粒子物理与原子核物理、原子分子物理专业必作)
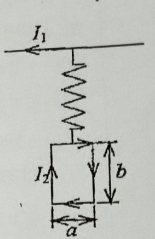
   载有稳恒电流 $I_1$ 的无限长直导线(看成刚体)下用一劲度系数为 $K$ 的轻质弹簧挂一载有稳恒电流 $I_2$ 的矩形线圈。设长直导线通电前弹簧长度为 $L_0$,通电后矩形线圈将向下移动一段距离，求当磁场对线圈作的功满足 $A=\mu_0I_1I_2a/2 \pi$ 时，线圈、弹簧、地球组成的系统的势能变化(忽略感应电流对 $I_2$ 的影响)。
   
   图 5
6. (各专业必作)
   薄钢片上有两条紧靠的平行细缝，用波长 $\lambda=546.1nm(1nm=10^-9m)$ 的平面光波正入射到钢片上。屏幕距双缝的距离为 $D=2.00m$，测得中央明条纹两侧的第五级明条纹间的距离为 $\delta x=12.0nm$。
   (1)求两缝间的距离。
   (2)从任一明条纹(记作 0)向一边数到第 20 条明条纹，共经过多大距离？
   (2)如果使光波斜入射到钢片上，条纹间距将如何改变？
7. (凝聚态物理、光学、生物医学物理、应用电子技术专业考生必作)
   用每毫米 $ 300 $ 条刻痕的衍射光栅来检验仅含有属于红和蓝的两种单色成分的光谱,已知红谱线波长 $\lambda_R$ 在 $0.63-0.76\mu m$ 范围内,蓝谱线波长 $\lambda_B$ 名在 $0.43-0.49 \mu m$ 范围内，当光垂直入射到光栅时，发现在衍射角为 24.46°处，红蓝两谱线同时出现。
   (1)在什么角度下红蓝两谱线还会同时出现？
   (2)在什么角度下只有红谱线出现？
8. (各专业必作)
   双星之间的角距离为 $1*10^{-6}rad$，其幅射波长为 5770A 和 5790A 两个波长。
   (1)望远镜的口径需要多大才能分辨此双星的像?
   (2)若要分辨此两波长，光栅条数应为多少?
9. ( 凝聚态物理、光学、生物医学物理、应用电子技术专业考生必作)
   一块厚度为 $0.04mm$ 的方解石晶片,其光轴平行于表面,将它插入正交偏振片之间，且使主截面与第一偏振片的透振方向成 $\theta$($\theta \neq 0,\theta \neq 90$°)角。试问哪些光不能透过该装置?已知方解石的 $n_0=1.658,n_e=1.486$。
10. (理论物理、粒子物理与原子核物理、原子分子物理专业必作)
    正弦光栅的屏函数为 $\widetilde t(x,y)=t_0+t_1 \cos\left(2\pi f_x x+2\pi f_y y\right) $，现将它沿斜方向平移 $\Delta r=(\Delta x,\Delta y)$。写出移动后的屏函数表达式。
11. (理论物理、粒子物理与原子核物理、原子分子物理专业必作)
    在偏振光干涉的装置中，两偏振片的透光方向夹角为 60°，两者之间插入一个顶角 $\alpha=30'$ 的石英尖劈，其光轴平行于表面，尖劈的主截面与两偏振片的透光方向都成 30°角。以波长 589.3nm 的钠黄光垂直入射。求:
    (1)透射光的光强分布； (2)干涉条纹的反衬度。已知石英的折射率 $n_0=1.54424,n_e=1.55335$。