最小二乘法拟合函数（Matlab）

贡献者： addis

预备知识　最小二乘法，Nelder-Mead 算法

　　我们在 “最小二乘法” 见到的三个例子中，方差函数都是待定系数的线性组合，这种情况下我们令偏导为零后得到的是线性方程组，便于求解。然而当方差不是待定系数的线性组合时，得到的方程组往往非常复杂，这时就需要借助数值计算。相比用数值计算解 $N$ 元的非线性方程组，更简单的方法是直接用数值方法寻找方差函数的极小值（如 Nelder-Mead 算法）。实践证明，大多数情况下极小值点仅有一个，那就是最小值点。

　　为了验证结果的正确性，我们先来用数值方法拟合 $A \cos (x + φ_{0}) + C$ ，并与 “最小二乘法” 中的方法比较结果。

图 1：运行结果

　　 Matlab 代码如下，需要 NelderMead.m 函数：

代码 1：curveFit_test.m

function curveFit_test
close all;
% 随机生成简谐曲线
N = 20;
x0 = linspace(0, 2*pi, N);
y0 = 5*rand * sin(x0 + 2*pi * rand) + 10 * rand;
y0 = y0 + 2*rand(1,20); % 产生随机误差
scatter(x0, y0, '+'); % 画出散点
hold on;

% Nelder-Mead 求方差最小值点
f = @(x) norm( x(1)*sin(x0 + x(2)) + x(3) - y0 )^2;
c = NelderMead(f, [5, 1, 5], 1e-7);
% 画拟合结果
x = linspace(0, 2*pi, 50);
y1 = c(1) * sin(x + c(2)) + c(3);
plot(x, y1);

% 解线性方程组求方差最小值点
c = sinfit(x0, y0);
% 画拟合结果
y2 = c(1)*cos(x) + c(2)*sin(x) + c(3);
plot(x, y2, '.');
end

% 拟合简谐曲线
% y = C(1)*cos(x) + C(2)*sin(x) + C(3)
function C = sinfit(x, y)
N = numel(x);
cosx = cos(x); sinx = sin(x);
sc = sum(sinx.*cosx);
s = sum(sinx); c = sum(cosx);
% 系数矩阵
M = [sum(cosx.^2), sc          , c;
               sc, sum(sinx.^2), s;
                c,            s, N];
b = [sum(y.*cosx); sum(y.*sinx); sum(y)];
C = M\b; % 解线性方程组
end

　　运行结果如图 1 所示，可见两种方法拟合出的曲线一致（红色的曲线和黄色的点线）。注意第 13 行使用了 “Nelder-Mead 算法” 中的函数 NelderMead 求函数句柄 f 的最小值。

　　一般参数函数的最小二乘法拟合代码为

代码 2：curveFit.m

% 最小二乘法拟合一元实函数，(x0,y0) 是数据点
% fun 是函数句柄， 格式 y = fun(x, p)， 需要支持矢量 x 输入
% p0 是函数初始参数， double 矢量
% 输出最优的 p 以及（局部）最小方差 s
% 使方差 sum(abs(fun(x0, p) - y0).^2) 最小
% p_err 是 NelderMead 算法中 p 的绝对误差
% 返回方均差 err2

function [p, err2] = curveFit(x0, y0, fun, p0, p_err)
% Nelder-Mead 求方差最小值点
f = @(p) sum((fun(x0, p) - y0).^2);
[p, sum_s2] = NelderMead(f, p0, p_err);
err2 = sum_s2 / numel(x0);
end

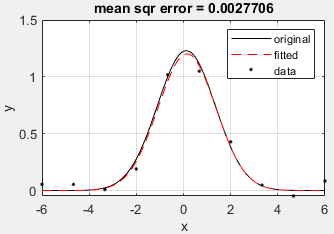
1. 例子：拟合高斯函数

图 2：高斯函数

A \exp [- (x - x_{m})^{2} / (2 σ^{2})]

的拟合（fit_gaussian_test.m）

代码 3：fit_gaussian.m

% fit a gaussian distribution
% return mean square error
function [A, xmid, sigma, s2] = fit_gaussian(x0, y0, p_err)
    fun = @(x, p) p(1) * exp(-(x-p(2)).^2 / (2*p(3)^2));
    [A, ind] = max(y0);
    xmid = x0(ind);
    sigma = abs(x0(end)-x0(1));
    p0 = [A, xmid, sigma];
    [p, s2] = curveFit(x0, y0, fun, p0, p_err);
    A = p(1); xmid = p(2); sigma = p(3);
end

代码 4：fit_gaussian_test.m

% === params ===
N = 10;
A = 1.23; xmid = 0.12; sigma = 1.23;
% ==============

x = linspace(x0(1), x0(end), 500);
x0 = linspace(-6, 6, N);
y0 = A*exp(-(x0-xmid).^2/(2*sigma^2));
y0_with_err = y0 + 0.2*(rand(1, N)-0.5);
[A_fit, xmid_fit, sigma_fit, s2] = fit_gaussian(x0, y0_with_err, 1e-10);

figure;
plot(x, A*exp(-(x-xmid).^2/(2*sigma^2)), 'k');
hold on;
plot(x, A_fit*exp(-(x-xmid_fit).^2/(2*sigma_fit^2)), 'r--');
plot(x0, y0_with_err, 'k.');
grid on;
xlabel x; ylabel y;
title("mean sqr error = " + mean(s2));
legend({'original', 'fitted', 'data'});

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。