荷质比的测定

贡献者： TongQing18; addis

预备知识　静电的基本规律和性质

1. 荷质比

　　¹原理：利用电子（或其他带电粒子）在磁场中偏转性的特点，测得粒子电荷与质量之比（即荷质比）说明：荷质比是带电微观粒子的基本参量之一。

　　典型的测量荷质比的方式有两种

2. 汤姆孙测量电子荷质比的方法

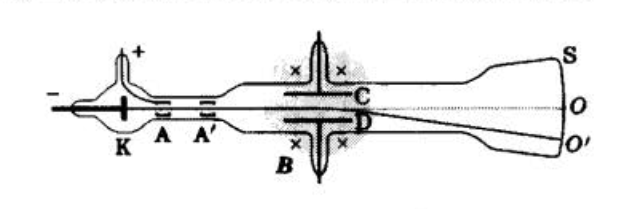
图 1：汤姆孙法测荷质比

　　玻璃管内抽成真空，在阳极 $A$ 与阴极 $K$ 之间维持数千伏特的电压，靠管内残存的气体的离子在阴极引起的二次发射产生电子流。阳极 $A$ 和第二个金属屏 $A'$ 中央各有一个小孔，$K$、$A$ 之间被加速了电子流，只有很窄一束能够通过两孔。玻璃管的中部 $C$、$D$ 为电容板的两极板，在其间可产生一竖直方向的电场。图中阴影部分，是由管外的电磁铁产生一方向垂直纸面的磁场。适当的调节电场和磁场的强度，可使它们作用在电子上的力达到平衡，即：

\begin{equation} eE=evB~. \end{equation}

　　然后，将电场切断，电子束在磁场区域内将沿圆弧运动，此圆弧半径可得：

\begin{equation} R=\frac {mv}{eB}~. \end{equation}

　　因此，电子的荷质比为：

\begin{equation} \frac{e}{m}=\frac{v}{RB}=\frac {E}{RB^2}~. \end{equation}

通过测得 $R$ 之后，我们就能求出荷质比了。

3. 磁聚焦法

图 2：磁聚焦法测荷质比

　　抽真空的玻璃管中装有热阴极 K 和有小孔的阳极 $A$。在 $A$，$K$ 之间加电压 $\Delta U$ 时，由阳极的小孔射出的电子动能为：

\begin{equation} \frac{1}{2}mv^2=e\Delta U~, \end{equation}

　　从得到其速率为：

\begin{equation} v=\sqrt{\frac{2e\Delta U}{m}}~. \end{equation}

在电容器 $C$ 上加一个不大的横向交变电场，使不同时刻通过这里的电子发生不同程度的偏转。在电容器 $C$ 和荧光屏 $S$ 之间加一均匀的纵向磁场，电子从 $C$ 出来后将沿螺旋线运动，到达距离 $h=\frac{2\pi mv}{eB}$ 的地方聚焦。适当的调节磁感应强度 $B$ 大小，使得电子流的焦点落在荧光屏 $S$ 上。其中 $h$ 是 $C$ 到 $S$ 间的距离。将上述方程中的 $v$ 消去，我们有：

\begin{equation} \frac {e}{m}=\frac{8\pi ^2 \Delta U}{h^2 B^2}~. \end{equation}

（上式中方程右边的各量都能够测出来，因此我们能够确定 $e/m$）

1. ^ 参考 [1]。

[1] ^ 赵凯华, 陈熙谋. 新概念物理教程电磁学 第二版

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。