微积分学（综述）

                     

贡献者： 待更新

　　 本文根据 CC-BY-SA 协议转载翻译自维基百科相关文章。

　　 微积分是研究连续变化的数学分支，正如几何学研究形状，代数学研究算术运算的推广一样。

　　 微积分最初被称为 “无穷小微积分” 或 “无穷小量的演算”，它有两个主要分支：微分学和积分学。微分学关注的是瞬时变化率和曲线的斜率，而积分学则研究量的累积以及曲线下方或两条曲线之间的面积。这两大分支通过微积分基本定理相互联系。它们都依赖于无穷数列和无穷级数收敛于确定极限的基本概念。\(^\text{[1]}\) 微积分是处理变量随时间或其他参照变量变化问题的 “数学支柱”。\(^\text{[2]}\)

　　 无穷小微积分在 17 世纪末分别由艾萨克·牛顿和戈特弗里德·威廉·莱布尼茨独立创立。\(^\text{[3][4]}\) 后来的工作，包括对极限概念的形式化，使这些发展建立在更坚实的概念基础之上。如今，微积分被广泛应用于科学、工程、生物学，甚至在社会科学和其他数学分支中也有重要应用。\(^\text{[5][6]}\)

1. 词源

　　 在数学教育中，微积分是无穷小微积分和积分微积分的缩写，指的是初等数学分析的课程。

　　 在拉丁语中，"calculus" 意为 “小卵石”（是 "calx" 的 diminutive 形式，意为 “石头”），这个含义在医学中仍然存在。由于这些小卵石被用来计算距离、计票和进行算盘运算，\(^\text{[7]}\) 这个词逐渐成为拉丁语中表示 “计算” 的词汇。在这个意义上，它至少在 1672 年就已经在英语中使用了，早于莱布尼茨和牛顿的出版物，他们的数学著作是用拉丁语写的。\(^\text{[8]}\)

　　 除了微分学和积分学，"calculus" 这个词也被用来命名一些特定的计算方法或理论，这些方法或理论暗示某种形式的计算。这种用法的例子包括命题微积分、里奇微积分、变分法微积分、\(\lambda\) 微积分、序列微积分和过程微积分。此外，“微积分” 一词也在伦理学和哲学中得到了不同的应用，如边沁的幸福计算法和伦理计算法。

2. 历史

　　 现代微积分是在 17 世纪的欧洲由艾萨克·牛顿和戈特弗里德·威廉·莱布尼茨独立发展起来的（他们几乎在同一时期首次发表）。但是微积分的元素最早出现在古埃及，随后是古希腊，接着是中国和中东地区，最后在中世纪的欧洲和印度再次出现。

古代先驱

　　 埃及

　　 体积和面积的计算（这是积分微积分的一个目标）可以在公元前 1820 年左右的埃及《莫斯科纸草书》中找到，但这些公式只是简单的指示，并未说明它们是如何得出的。\(^\text{[9][10]}\)

　　 希腊

图
图 1：阿基米德在他的著作《抛物线的求积》中使用了穷尽法来计算抛物线下的面积。

　　 为积分微积分奠定基础并预示着极限概念的到来，古希腊数学家克尼多斯的欧多克索斯（公元前 390–337 年）发展了穷尽法，用于证明圆锥体和金字塔体积的公式。

　　 在希腊化时期，这一方法被阿基米德（公元前 287 年–公元前 212 年）进一步发展，他将其与 “不可分物” 概念结合——这是无穷小量的先驱——使他能够解决许多现在由积分微积分处理的问题。例如，在《机械定理法》中，他描述了如何计算固体半球的重心、圆形抛物体的圆台的重心，以及由抛物线和其一条割线所围成的区域的面积。\(^\text{[11]}\)

　　 中国

　　 穷尽法后来由中国的刘徽在公元 3 世纪独立发现，用于求解圆的面积。\(^\text{[12][13]}\) 在公元 5 世纪，祖耕之，祖冲之的儿子，建立了一种方法 \(^\text{[14][15]}\)，后来被称为卡瓦列里的原理，用于求解球体的体积。

中世纪

图
图 2：伊本·海赛姆，11 世纪阿拉伯数学家和物理学家
图
图 3：印度数学家和天文学家婆罗摩笃二世

　　 中东

　　 在中东，哈桑·伊本·海赛姆（拉丁化为阿尔哈泽姆，约公元 965 年–约 1040 年）推导出了四次方和的公式。他确定了计算由曲线 \(y = x^k\) 所围成的面积的方程（这在现代符号中表示为积分 \(\int x^k \, dx\)），适用于任何给定的非负整数值 \(k\)。\(^\text{[16]}\) 他利用这些结果进行了现在所称的该函数的积分，其中关于整数平方和和四次方和的公式使他能够计算出抛物面体的体积。\(^\text{[17]}\)

　　 印度

　　 婆罗摩笃二世（约公元 1114–1185 年）熟悉一些微分学的思想，并提出 “微分系数” 在函数的极值点处为零。\(^\text{[18]}\) 在他的天文学著作中，他给出了一个类似于无穷小方法的程序。具体来说，如果 \(x \approx y\)，则 \( \sin\left(y\right) - \sin\left(x\right) \approx (y - x) \cos\left(y\right) \).这可以解释为发现余弦是正弦的导数。\(^\text{[19]}\) 在 14 世纪，印度数学家提出了一种不严格的方法，类似于微分法，适用于某些三角函数。桑伽马格拉的马达瓦和喀拉拉天文学与数学学派提出了微积分的组成部分。他们研究了与麦克劳林级数等价的级数，例如 \( \sin\left(x\right) \)、\( \cos\left(x\right) \) 和 \( \arctan\left(x\right) \)，比它们在欧洲的引入早了两百多年。\(^\text{[20]}\) 根据 Victor J. Katz 的说法，他们未能 “将许多不同的思想结合在一起，并统一为导数和积分两个主题，展示它们之间的联系，并将微积分转化为我们今天所拥有的强大问题解决工具”。\(^\text{[17]}\)

现代

　　 约翰内斯·开普勒的著作《酒桶的立体几何学》（Stereometria Doliorum，1615 年）为积分微积分奠定了基础。\(^\text{[21]}\) 开普勒发展了一种方法，通过将从椭圆焦点绘制的许多半径的长度相加，来计算椭圆的面积。\(^\text{[22]}\)

　　 一个重要的工作是由博纳文图拉·卡瓦列里撰写的论文，起源于开普勒的方法，\(^\text{[22]}\) 卡瓦列里主张体积和面积应通过将无穷小厚度的截面的体积和面积相加来计算。这些思想与阿基米德在《方法》中的思想相似，但该论文在 13 世纪被认为已经失传，直到 20 世纪初才被重新发现，因此卡瓦列里当时并不知晓这篇论文。卡瓦列里的工作并未受到高度评价，因为他的方法可能导致错误的结果，而且他引入的无穷小量在最初被认为是可疑的。

　　 微积分的正式研究将卡瓦列里的无穷小量与大约同一时期在欧洲发展起来的有限差分法结合在一起。皮埃尔·德·费马声称他借鉴了丢番图的思想，引入了 “相等” 这一概念，表示在一个无穷小的误差项下的相等。\(^\text{[23]}\) 这一结合是由约翰·沃利斯、艾萨克·巴罗和詹姆斯·格雷戈里完成的，后两者在约 1670 年证明了微积分第二基本定理的前身。\(^\text{[24][25]}\)

　　 乘积法则和链式法则，\(^\text{[26]}\) 高阶导数和泰勒级数的概念，\(^\text{[27]}\) 以及解析函数的概念 \(^\text{[28]}\) 都被艾萨克·牛顿在他特有的符号体系中使用，该符号体系用于解决数学物理问题。在他的著作中，牛顿将自己的思想重新表述，以适应当时的数学语言，将无穷小量的计算替换为等价的几何论证，这些论证被认为是无可指摘的。他使用微积分的方法解决了行星运动问题、旋转流体表面的形状问题、地球的扁率问题、沿摆线滑动的重物运动问题，以及他在《自然哲学的数学原理》（1687 年）中讨论的许多其他问题。在其他工作中，他为函数发展了级数展开，包括分数和无理幂，显然他已经理解了泰勒级数的原理。他并未公开所有这些发现，当时无穷小方法仍然被认为是不可靠的。\(^\text{[29]}\)

图
图 4：戈特弗里德·威廉·莱布尼茨是第一个清楚地陈述微积分规则的人。
图
图 5：艾萨克·牛顿在他的运动定律和万有引力定律中发展了微积分的应用。

　　 这些思想被戈特弗里德·威廉·莱布尼茨整理成了真正的无穷小微积分，最初他被牛顿指控抄袭。\(^\text{[30]}\) 现在他被认为是微积分的独立发明者和贡献者。他的贡献在于提供了一套清晰的规则来处理无穷小量，从而允许计算二阶及更高阶的导数，并提供了乘积法则和链式法则的微分和积分形式。与牛顿不同，莱布尼茨在符号的选择上付出了极大的努力。\(^\text{[31]}\)

　　 今天，莱布尼茨和牛顿通常都被认为是独立发明并发展了微积分。牛顿是第一个将微积分应用于一般物理学的人。莱布尼茨发展了今天微积分中使用的大部分符号。\(^\text{[32]: 51–52}\) 牛顿和莱布尼茨提供的基本见解包括微分和积分定律，强调微分和积分是逆过程，二阶及更高阶导数，以及近似多项式级数的概念。

　　 当牛顿和莱布尼茨首次发布他们的成果时，关于哪位数学家（因此也涉及哪个国家）应当获得荣誉，发生了激烈的争论。牛顿首先得出了他的结果（后来在《流量法则》中发表），但莱布尼茨首先发布了他的《最大值和最小值的新方法》。牛顿声称莱布尼茨从他未出版的笔记中窃取了思想，这些笔记是牛顿与皇家学会的几位成员共享的。这场争论使得讲英语的数学家与大陆欧洲的数学家之间产生了长期的分裂，这对英国数学发展造成了不利影响。\(^\text{[33]}\) 通过仔细审查莱布尼茨和牛顿的论文，可以发现他们是独立得出结果的，莱布尼茨首先从积分开始，而牛顿则从微分开始。然而，正是莱布尼茨为这一新学科命名。牛顿称他的微积分为 “流量学”，这一术语在 19 世纪的英国学校中一直沿用。\(^\text{[34]: 100}\) 使用莱布尼茨符号的第一部完整的微积分著作，直到 1815 年才以英文发布。\(^\text{[35]}\)

图
图 6：玛丽亚·盖塔娜·阿涅西

　　 自莱布尼茨和牛顿时代以来，许多数学家为微积分的持续发展做出了贡献。第一部涵盖无穷小微积分和积分微积分的最早且最完整的著作之一，是由玛丽亚·盖塔娜·阿涅西于 1748 年撰写的。\(^\text{[36][37]}\)

基础

　　 在微积分中，基础指的是从公理和定义出发，对该学科的严格发展。在早期的微积分中，无穷小量的使用被认为是不严谨的，并且受到几位作者的猛烈批评，最著名的批评者包括米歇尔·罗尔和伯克利主教。伯克利在 1734 年出版的《分析师》一书中，著名地将无穷小量描述为 “已故量的幽灵”。为微积分构建严格的基础，几乎占据了牛顿和莱布尼茨之后整个世纪的数学家的时间，至今仍然是一个活跃的研究领域。\(^\text{[38]}\)

　　 几位数学家，包括麦克劳林，曾试图证明使用无穷小量的合理性，但直到 150 年后，随着柯西和魏尔斯特拉斯的工作，最终找到了避免单纯使用 “无穷小量” 概念的方法。\(^\text{[39]}\) 微分和积分微积分的基础得以奠定。在柯西的《分析课程》中，我们可以找到一系列基础性的理论，包括通过无穷小量定义的连续性，以及在微分定义中（某种不够精确的）原型 \((\varepsilon,\delta)\) 极限定义。\(^\text{[40]}\) 在他的工作中，魏尔斯特拉斯正式化了极限的概念，并消除了无穷小量（尽管他的定义可以验证零平方无穷小量）。在魏尔斯特拉斯的工作之后，最终基于极限而非无穷小量来构建微积分成为常态，尽管这个学科偶尔仍被称为 “无穷小微积分”。伯尔纳德·黎曼利用这些思想为积分提供了精确的定义。\(^\text{[41]}\) 正是在这一时期，微积分的思想被推广到复平面，伴随着复分析的发展。\(^\text{[42]}\)

　　 在现代数学中，微积分的基础被包含在实分析领域中，该领域提供了微积分定理的完整定义和证明。微积分的应用范围也得到了极大的扩展。亨利·勒贝格发明了测度理论，基于埃米尔·博雷尔的早期发展，并用它来定义除最病态函数之外的所有函数的积分。\(^\text{[43]}\) 劳伦特·施瓦茨引入了分布理论，分布可以用来对任何函数求导。\(^\text{[44]}\)

　　 极限并不是微积分基础的唯一严谨方法。另一种方法是使用亚伯拉罕·罗宾逊的非标准分析。罗宾逊的方法，发展于 1960 年代，利用数学逻辑中的技术工具，将无穷小和无穷大数引入实数系统，类似于最初牛顿-莱布尼茨的构想。由此产生的数被称为超实数，它们可以用来给出类似于莱布尼茨式的发展，遵循通常的微积分规则。\(^\text{[45]}\) 还有平滑无穷小分析，它与非标准分析不同，因为它要求在推导过程中忽略高阶无穷小量。\(^\text{[38]}\) 平滑无穷小分析基于 F.W.劳维尔的思想，并采用范畴理论的方法，视所有函数为连续的，且无法用离散实体来表示。这一表述的一个方面是排中律不成立。\(^\text{[38]}\) 排中律在构造性数学中也被否定，构造性数学是数学的一个分支，它坚持认为，证明一个数字、函数或其他数学对象的存在应该给出该对象的构造。构造性框架下的微积分重构通常是构造性分析的主题之一。\(^\text{[38]}\)

重要性

　　 尽管微积分的许多思想早在希腊、中国、印度、伊拉克、波斯和日本就已出现，但微积分的使用始于 17 世纪的欧洲，当时牛顿和莱布尼茨在早期数学家的基础上建立了微积分的基本原理。\(^\text{[13][29][46]}\) 匈牙利博学家约翰·冯·诺依曼曾写道：

　　 “微积分是现代数学的第一个成就，其重要性难以过高估计。我认为它比其他任何事情都更明确地定义了现代数学的起点，而数学分析体系（作为其逻辑发展）仍然构成精确思维中的最大技术进步。”\(^\text{[47]}\)

　　 微分微积分的应用包括涉及速度和加速度的计算、曲线的斜率以及优化问题。\(^\text{[48]: 341–453}\) 积分微积分的应用包括涉及面积、体积、弧长、质心、功和压力的计算。\(^\text{[48]: 685–700 }\) 更高级的应用包括幂级数和傅里叶级数。

　　 微积分还被用来更精确地理解空间、时间和运动的性质。几个世纪以来，数学家和哲学家们一直在与涉及除以零或无穷多个数的和的悖论作斗争。这些问题在运动和面积的研究中出现。古希腊哲学家芝诺给出了几个著名的悖论例子。微积分提供了工具，特别是极限和无穷级数，用来解决这些悖论。\(^\text{[49]}\)

3. 原理

极限与无穷小量

　　 微积分通常通过处理非常小的量来发展。历史上，最初的处理方法是通过无穷小量。无穷小量是可以像实数一样处理的对象，但在某种意义上，它们是 “无限小” 的。例如，一个无穷小数可能大于 0，但小于序列 1、1/2、1/3、... 中的任何数字，因此小于任何正实数。从这个角度看，微积分是处理无穷小量的技术集合。符号 \(dx\) 和 \(dy\) 被认为是无穷小量，而导数 \(dy/dx\) 是它们的比值。\(^\text{[38]}\)

　　 无穷小量的方法在 19 世纪逐渐不再流行，因为难以精确定义无穷小量的概念。在 19 世纪末，无穷小量在学术界被极限的 \(\varepsilon-\delta\) 方法所取代。极限通过描述函数在某一输入值处的行为，表示其在邻近输入处的值。它们通过实数系统的内在结构（作为具有最小上界性质的度量空间）来捕捉小尺度的行为。在这种处理方法中，微积分是一系列操作特定极限的技术。无穷小量被越来越小的数列所取代，函数的无限小行为通过对这些数列取极限来找到。极限被认为为微积分提供了更严谨的基础，因此，在 20 世纪成为了标准方法。然而，20 世纪出现了无标准分析和平滑无穷小分析，这些方法为无穷小量的操作提供了坚实的基础，从而复兴了无穷小量的概念。\(^\text{[38]}\)

微分学

图
图 7：在 \((x_0, f(x_0))\) 处的切线。曲线在某一点的导数 \(f'(x)\) 是该点切线的斜率（纵向变化除以横向变化）。

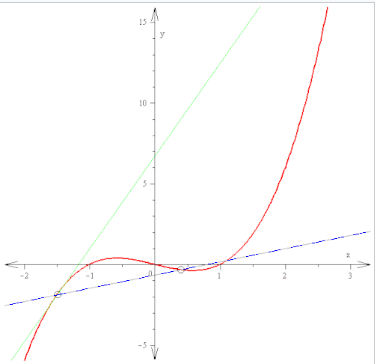
　　 微分学是研究函数导数的定义、性质和应用的学科。求导的过程称为微分。给定一个函数和它定义域中的一个点，某一点的导数是对该点附近函数小尺度行为的一种编码方式。通过在函数定义域的每个点上求导，可以得到一个新的函数，称为导数函数，或简称为原函数的导数。用正式的术语来说，导数是一个线性算子，它将一个函数作为输入，并产生一个新的函数作为输出。这比许多初等代数中研究的过程更为抽象，在初等代数中，函数通常输入一个数字并输出另一个数字。例如，如果倍增函数的输入是 3，则输出是 6；如果平方函数的输入是 3，则输出是 9。然而，导数可以将平方函数作为输入。这意味着导数会获取平方函数的所有信息——例如，2 映射到 4，3 映射到 9，4 映射到 16，依此类推——并使用这些信息生成另一个函数。通过对平方函数进行微分，得到的函数实际上是倍增函数。\(^\text{[32]: 32}\) 

　　 更明确地说，“倍增函数” 可以表示为 \( g(x) = 2x \)，而 “平方函数” 可以表示为 \( f(x) = x^2\)。“导数” 现在将由表达式 “\(x^2\)” 定义的函数 \( f(x) \) 作为输入，即所有的信息——例如，2 映射到 4，3 映射到 9，4 映射到 16，依此类推——并利用这些信息输出另一个函数，函数 \( g(x) = 2x \)，如前所述。

　　 在拉格朗日符号中，导数的符号是类似撇号的符号，称为 “素”（prime）。因此，一个名为 \( f \) 的函数的导数表示为 \( f' \)，读作 “f prime” 或 “f dash”。例如，如果 \( f(x) = x^2 \) 是平方函数，那么 \( f'(x) = 2x \) 就是它的导数（即上文中的倍增函数 \( g \)）。

　　 如果函数的输入代表时间，则导数表示关于时间的变化。例如，如果 \( f \) 是一个以时间为输入，给出某时刻球的位置为输出的函数，那么 \( f \) 的导数就是位置随时间变化的速率，即球的速度。\(^\text{[32]: 18–20 }\) 

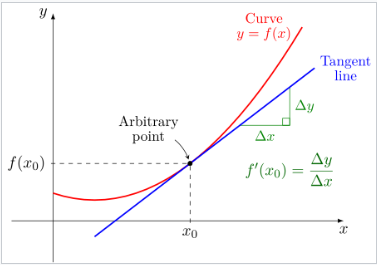
　　 如果一个函数是线性的（即函数的图像是一条直线），那么该函数可以写成 \(y = mx + b\)，其中 \(x\) 是自变量，\(y\) 是因变量，\(b\) 是 \(y\)-截距，且： \[ m = \frac{\text{rise}}{\text{run}} = \frac{\text{change in } y}{\text{change in } x} = \frac{\Delta y}{\Delta x}.~ \] 这给出了直线斜率的确切值。\(^\text{[50]: 6 }\)  然而，如果函数的图像不是直线，则 \(y\) 的变化量除以 \(x\) 的变化量会变化。导数为关于输入变化引起的输出变化提供了一个精确的定义。具体来说，设 \(f\) 是一个函数，并且固定 \(f\) 定义域中的一个点 \(a\)。\((a, f(a))\) 是函数图像上的一个点。如果 \(h\) 是一个接近零的数，那么 \(a + h\) 是一个接近 \(a\) 的数。因此，\((a + h, f(a + h))\) 接近于 \((a, f(a))\)。这两点之间的斜率是： \[ m = \frac{f(a+h) - f(a)}{(a+h) - a} = \frac{f(a+h) - f(a)}{h}.~ \] 这个表达式叫做差商。通过曲线上的两个点的直线称为割线，因此 \(m\) 是通过点 \((a, f(a))\) 和 \((a + h, f(a + h))\) 的割线的斜率。第二条线仅仅是函数在点 \(a\) 处行为的一个近似，因为它没有考虑 \(a\) 和 \(a + h\) 之间发生的情况。通过将 \(h\) 设为零来发现 \(a\) 处的行为是不可能的，因为这会导致除以零，而除以零是未定义的。导数的定义是通过取极限，当 \(h\) 趋近于零时，这意味着它考虑了所有小值 \(h\) 时 \(f\) 的行为，并且为当 \(h\) 等于零时提取一个一致的值： \[ \lim_{h \to 0} \frac{f(a+h) - f(a)}{h}.~ \] 从几何上看，导数是函数 \(f\) 在 \(a\) 处图像的切线的斜率。切线是割线的极限，正如导数是差商的极限一样。因此，导数有时被称为函数 \(f\) 的斜率。\(^\text{[50]: 61–63 }\)  

图
图 8：曲线在某一点的导数 \( f'(x) \) 是该点切线的斜率。这个斜率是通过考虑第二条线斜率的极限值来确定的。这里涉及的函数（以红色表示）是 \( f(x) = x^3 - x \)。通过点 \((-3/2, -15/8)\) 的切线（以绿色表示）具有斜率 \( 23/4 \)。图中的垂直和水平方向的尺度不同。

　　 这是一个具体的例子，平方函数在输入为 3 时的导数。设 \(f(x) = x^2\) 为平方函数。 \[ \begin{aligned} f'(3) &= \lim_{h \to 0} \frac{(3+h)^2 - 3^2}{h} \\ &= \lim_{h \to 0} \frac{9 + 6h + h^2 - 9}{h} \\ &= \lim_{h \to 0} \frac{6h + h^2}{h} \\ &= \lim_{h \to 0} (6 + h) \\ &= 6 \end{aligned}~ \] 平方函数在点 \((3, 9)\) 处的切线的斜率是 6，也就是说，它向上变化的速度是向右变化速度的六倍。刚才描述的极限过程可以在平方函数定义域的任何点上进行。这定义了平方函数的导数函数，或简称为平方函数的导数。与上面类似的计算表明，平方函数的导数是倍增函数。\(^\text{[50]: 63 }\) 

莱布尼茨符号

　　 莱布尼茨引入的常用符号，用于表示上面例子中的导数是： \[ y = x^2 ~ \] \[\frac{dy}{dx} = 2x.~ \] 在基于极限的方法中，符号 \(\frac{dy}{dx}\) 不应被解释为两个数字的商，而应被视为上面计算的极限的简写。\(^\text{[50]: 74 }\)  然而，莱布尼茨确实打算将其表示为两个无穷小数的商，其中 \(dy\) 是由于对 \(x\) 施加无穷小变化 \(dx\) 引起的 \(y\) 的无穷小变化。我们也可以将 \(\frac{d}{dx}\) 视为一个微分算子，它将一个函数作为输入，并将另一个函数，即导数，作为输出。例如： \[ \frac{d}{dx}(x^2) = 2x.~ \] 在这种用法中，分母中的 \(dx\) 读作 “相对于 \(x\)”。\(^\text{[50]: 79 }\) 另一个正确符号的例子可能是： \[ g(t) = t^2 + 2t + 4~ \] \[ \frac{d}{dt} g(t) = 2t + 2.~ \] 即使在使用极限而非无穷小量开发微积分时，通常也会像处理实数一样操作符号 \(dx\) 和 \(dy\)；尽管可以避免这种操作，但它们在表达诸如全导数等操作时在符号上是方便的。

积分学

图
图 9
图
图 10

　　 积分学是研究两个相关概念的定义、性质和应用的学科，分别是不定积分和定积分。求解积分的过程称为积分。\(^\text{[48]: 508  }\) 不定积分，也称为反导数，是导数的逆运算。\(^\text{[50]: 163–165}\) 当 \(f\) 是 \(F\) 的导数时，\(F\) 是 \(f\) 的不定积分。（在微积分中，使用大写和小写字母来表示函数及其不定积分是很常见的。）定积分输入一个函数并输出一个数字，这个数字表示输入函数与 \(x\)-轴之间的面积的代数和。定积分的技术定义涉及面积和矩形的总和的极限，称为黎曼和。\(^\text{[51]: 282  }\)

　　 一个激励性的例子是给定时间内所经过的距离。\(^\text{[50]: 153  }\) 如果速度是恒定的，则只需乘法即可： \[ \text{Distance} = \text{Speed} \cdot \text{Time}~ \] 但是，如果速度发生变化，则需要更强大的方法来计算距离。一个这样的计算方法是通过将时间分割成许多短的时间间隔来逼近所经过的距离，然后将每个间隔中经过的时间乘以该间隔内的速度，再对每个间隔中的近似距离求和（一个黎曼和）。基本思想是，如果只经过很短的时间，则速度大致保持不变。然而，黎曼和只能给出所经过距离的近似值。我们必须对所有这样的黎曼和取极限，以找到确切的所经过的距离。

　　 当速度恒定时，可以通过将速度和时间相乘来计算在给定时间间隔内所经过的总距离。例如，以 50 英里每小时的速度行驶 3 小时，总距离为 150 英里。将速度绘制为时间的函数，得到一个矩形，矩形的高度等于速度，宽度等于经过的时间。因此，速度和时间的乘积也计算了（恒定）速度曲线下的矩形面积。\(^\text{[48]: 535  }\) 这种曲线下的面积与所经过距离之间的联系可以扩展到任何不规则形状的区域，这些区域在给定时间内表现出波动的速度。如果 \(f(x)\) 表示速度随时间的变化，那么在时间 \(a\) 和 \(b\) 之间所经过的距离就是 \(f(x)\) 与 \(x\)-轴之间区域的面积，范围在 \(x = a\) 和 \(x = b\) 之间。

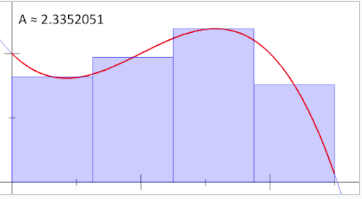
　　 为了逼近该面积，一种直观的方法是将 \(a\) 和 \(b\) 之间的距离分成若干个相等的段，每段的长度用符号 \(\Delta x\) 表示。对于每个小段，我们可以选择函数 \(f(x)\) 的一个值，称为该值为 \(h\)。然后，底边为 \(\Delta x\)，高为 \(h\) 的矩形的面积给出了该段所经过的距离（时间 \(\Delta x\) 乘以速度 \(h\)）。与每个小段相关的是其上方函数的平均值 \(f(x) = h\)。所有这些矩形的总和给出了曲线与轴之间面积的近似，这也是所经过总距离的近似值。较小的 \(\Delta x\) 会产生更多的矩形，并且在大多数情况下会提供更好的近似，但为了得到精确的答案，我们需要对 \(\Delta x\) 取极限，当 \(\Delta x\) 趋近于零时。\(^\text{[48]: 512–522  }\) 

　　 积分的符号是 \(\int\)，一个被拉长的 S，旨在提示求和。\(^\text{[48]: 529  }\) 定积分写作： \[ \int_{a}^{b} f(x)\, dx~ \] 并读作 “从 \(a\) 到 \(b\) 的 \(f(x)\) 对 \(x\) 的积分”。莱布尼茨符号中的 \(dx\) 用来提示将曲线下的面积分割成无穷多个矩形，使得它们的宽度 \(\Delta x\) 变成无穷小的 \(dx\)。\(^\text{[32]: 44}\)

　　 不定积分或反导数写作： \[ \int f(x)\, dx.~ \] 仅相差一个常数的函数有相同的导数，可以证明一个给定函数的反导数是一类仅相差一个常数的函数。\(^\text{[51]: 326}\) 由于函数 \(y = x^2 + C\) 的导数为 \(y' = 2x\)，其中 \(C\) 是任何常数，因此后者的反导数为： \[ \int 2x\, dx = x^2 + C.~ \] 不定积分或反导数中未指定的常数 \(C\) 被称为积分常数。\(^\text{[52]: 135 }\) 

基本定理

　　 微积分的基本定理表明，微分和积分是逆运算。\(^\text{[51]: 290 }\)  更准确地说，它将反导数的值与定积分联系起来。因为通常计算反导数比应用定积分的定义更容易，所以微积分的基本定理提供了一种计算定积分的实用方法。它也可以被解释为微分是积分的逆运算这一事实的精确表述。

　　 微积分的基本定理指出：如果函数 \(f\) 在区间 \([a, b]\) 上连续，并且 \(F\) 是一个在区间 \((a, b)\) 上，其导数为 \(f\) 的函数，那么： \[ \int_{a}^{b} f(x)\, dx = F(b) - F(a).~ \] 此外，对于区间 \((a, b)\) 内的每个 \(x\)， \[ \frac{d}{dx} \int_{a}^{x} f(t)\, dt = f(x).~ \] 这一发现由牛顿和莱布尼茨同时提出，是他们的工作被广泛传播后，解析结果得以迅速发展的关键。（由于牛顿和莱布尼茨之间的优先权争议，牛顿和莱布尼茨受到直接前辈的影响程度，尤其是莱布尼茨可能从艾萨克·巴罗的工作中学到的内容，仍然很难确定。\(^\text{[53]}\)）基本定理提供了一种代数方法，用于计算许多定积分——无需执行极限过程——通过找到反导数的公式。它也是微分方程的原型解。微分方程将一个未知函数与其导数联系起来，并在科学中无处不在。\(^\text{[54]: 351–352 }\)

4. 应用

图
图 11：鹦鹉螺壳的对数螺线是一个经典的形象，用来描绘与微积分相关的增长和变化。

　　 微积分应用于所有物理科学的分支、精算学、计算机科学、统计学、工程学、经济学、商业、医学、人口学以及其他可以用数学模型表示并且需要最优解的领域。它使得我们可以从（非常数的）变化率推导出总变化，或者反过来。在研究问题时，我们常常已知其中一个量，而试图找出另一个量。微积分还可以与其他数学学科结合使用。例如，它可以与线性代数结合，用来找到一组点在某个领域的 “最佳拟合” 线性近似。或者，它也可以与概率论结合，利用概率密度函数来确定连续随机变量的期望值。在解析几何中，研究函数图像时，微积分被用来找到极大值和极小值、斜率、凹凸性以及拐点。微积分还被用于求解方程的近似解；在实际应用中，它是解决微分方程和进行根求解的标准方法。例如，像牛顿法、固定点迭代法和线性近似法等方法都是常见的微积分应用。比如，航天器使用欧拉法的变种来在零重力环境下近似曲线航行路径。

　　 物理学特别依赖微积分；经典力学和电磁学中的所有概念都是通过微积分联系在一起的。已知密度物体的质量、物体的转动惯量以及由于引力和电磁力所产生的势能，都可以通过微积分来求解。微积分在力学中的一个应用例子是牛顿的第二定律，它表明物体动量关于时间的导数等于作用在物体上的合力。另一种表达牛顿第二定律的方式是说，合力等于物体的质量乘以加速度，而加速度是速度的时间导数，因此也是物体位置的二阶时间导数。从已知物体加速度的情况下，我们可以使用微积分推导出物体的轨迹。\(^\text{[59]}\)

　　 麦克斯韦的电磁学理论和爱因斯坦的广义相对论理论也都是用微分微积分的语言来表达的。\(^\text{[60][61]: 52–55 }\) 化学中也使用微积分来确定反应速率，\(^\text{[62]: 599}\) 以及研究放射性衰变。\(^\text{[62]: 814 }\) 在生物学中，种群动态通过生育率和死亡率来建模种群变化。\(^\text{[63][64]: 631 }\)

　　 格林定理给出了围绕简单闭合曲线 \(C\) 的线积分与由 \(C\) 边界围成的平面区域 \(D\) 上的双重积分之间的关系，它被应用在一种叫做平面仪的仪器中，用于计算图纸上平面表面的面积。\(^\text{[65]}\) 例如，它可以用于计算设计房产布局时不规则形状的花坛或游泳池所占的面积。

　　 在医学领域，微积分可以用来找到血管的最佳分支角度，从而最大化血流量。\(^\text{[66]}\) 微积分还可以应用于理解药物从体内的清除速度，或癌性肿瘤的生长速度。\(^\text{[67]}\)

　　 在经济学中，微积分允许通过提供一种简便的方式来计算边际成本和边际收益，从而确定最大利润。\(^\text{[68]: 387 }\)

5. 另见

6. 参考文献

  1. DeBaggis, Henry F.; Miller, Kenneth S. (1966). 《微积分的基础》. 费城: Saunders. OCLC 527896.
  2. Fox, Huw; Bolton, Bill (2002). 《微积分》. 载于《工程师与技术专家数学》. Elsevier. 第 99–158 页. doi:10.1016/b978-075065544-6/50005-9. ISBN 978-0-7506-5544-6. 于 2024 年 11 月 24 日检索.
  3. Boyer, Carl B. (1959). 《微积分的历史及其概念发展》. 纽约: Dover. 第 47、187–188 页. OCLC 643872.
  4. Bardi, Jason Socrates (2006). 《微积分战争：牛顿、莱布尼茨与史上最伟大的数学交锋》. 纽约: Thunder's Mouth Press. ISBN 1-56025-706-7.
  5. Hoffmann, Laurence D.; Bradley, Gerald L. (2004). 《商业、经济、社会与生命科学微积分》（第 8 版）. 波士顿: McGraw Hill. ISBN 0-07-242432-X.
  6. 《艾萨克·牛顿如何通过发明微积分改变世界》. www.mathtutordvd.com. 2017 年 3 月 18 日. 于 2024 年 11 月 26 日检索.
  7. 例如：
    • 《历史——古罗马帝国是否有计价出租车四处奔忙？》. Skeptics Stack Exchange. 2020 年 6 月 17 日. 存档于 2012 年 5 月 25 日. 于 2022 年 2 月 13 日检索.
    • Cousineau, Phil (2010). 《词汇捕手：奇异美妙词汇世界的奥德赛》. Simon and Schuster. 第 58 页. ISBN 978-1-57344-550-4. OCLC 811492876. 存档于 2023 年 3 月 1 日. 于 2022 年 2 月 15 日检索.
  8. 《calculus》. 《牛津英语词典》（网络版）. 牛津大学出版社.（需订阅或所属机构参与）.
  9. Kline, Morris (1990). 《古今数学思想（第一卷）》. 牛津大学出版社. 第 15–21 页. ISBN 978-0-19-506135-2. 存档于 2023 年 3 月 1 日. 于 2022 年 2 月 20 日检索.
  10. Imhausen, Annette (2016). 《古埃及数学：背景历史》. 普林斯顿大学出版社. 第 112 页. ISBN 978-1-4008-7430-9. OCLC 934433864.
  11. 例如：
    • Powers, J. (2020 年). 《阿基米德是否研究过微积分？》(PDF). 美国数学协会. 存档(PDF)于 2022 年 10 月 9 日.
    • Jullien, Vincent (2015 年). 《阿基米德与不可分量》. 载于《十七世纪不可分量再探》（科学网络·历史研究 第 49 卷）. 查姆: 施普林格国际出版. 第 451–457 页. doi:10.1007/978-3-319-00131-9_18. ISBN 978-3-319-00130-2. ISSN 1421-6329.
    • Plummer, Brad (2006 年 8 月 9 日). 《现代 X 射线技术揭示阿基米德数学理论被伪画覆盖》. 斯坦福大学. 存档于 2022 年 1 月 20 日. 于 2022 年 2 月 28 日检索.
    • 阿基米德 (2004 年). 《阿基米德著作集（第一卷）：论球与圆柱两书》. Reviel Netz 译. 剑桥大学出版社. ISBN 978-0-521-66160-7.
    • Gray, Shirley; Waldman, Cye H. (2018 年 10 月 20 日). 《阿基米德再探：从〈方法论〉看质心应用》. 《大学数学期刊》第 49 卷第 5 期，第 346–352 页. doi:10.1080/07468342.2018.1524647. ISSN 0746-8342. S2CID 125411353.
  12. Dun, Liu; Fan, Dainian; Cohen, Robert Sonné (1966 年). 《阿基米德与刘徽的圆研究比较》. 载于《中国科学技术史与科学哲学研究》第 130 卷. Springer. 第 279 页. ISBN 978-0-7923-3463-7. 存档于 2023 年 3 月 1 日. 于 2015 年 11 月 15 日检索., 第 279 页及以下，存档于 2023 年 3 月 1 日，来自 Wayback Machine
  13. Fan, Dainian; Cohen, R. S. (1996 年). 《中国科学技术史与科学哲学研究》. 多德雷赫特: Kluwer Academic Publishers. ISBN 0-7923-3463-9. OCLC 32272485.
  14. Katz, Victor J. (2008 年). 《数学史》（第 3 版）. 波士顿: Addison-Wesley. 第 203 页. ISBN 978-0-321-38700-4.
  15. Zill, Dennis G.; Wright, Scott; Wright, Warren S. (2009 年). 《微积分：早期超越函数》（第 3 版）. Jones & Bartlett Learning. 第 xxvii 页. ISBN 978-0-7637-5995-7. 存档于 2023 年 3 月 1 日. 于 2015 年 11 月 15 日检索. 第 27 页节选，存档于 2023 年 3 月 1 日，来自 Wayback Machine
  16. Dennis, David; Kreinovich, Vladik; Rump, Siegfried M. (1998 年 5 月 1 日). 《区间与微积分的起源》. 《可靠计算》第 4 卷第 2 期，第 191–197 页. doi:10.1023/A:1009989211143. ISSN 1573-1340.
  17. Katz, Victor J. (1995 年 6 月). 《伊斯兰与印度的微积分思想》. 《数学杂志》第 68 卷第 3 期，第 163–174 页. doi:10.1080/0025570X.1995.11996307. ISSN 0025-570X. JSTOR 2691411.
  18. Shukla, Kripa Shankar (1984 年). 《印度数学中的微积分应用》. 《印度科学史杂志》第 19 卷，第 95–104 页.
  19. Cooke, Roger (1997 年). 《印度人的数学》. 载于《数学简史》. Wiley-Interscience. 第 213–215 页. ISBN 0-471-18082-3.
  20. 《马德哈瓦——生平》. 数学史网. 于 2025 年 2 月 18 日检索.
  21. 《约翰内斯·开普勒：生平、定律与时代》. 美国国家航空航天局. 2016 年 9 月 24 日. 存档于 2021 年 6 月 24 日. 于 2021 年 6 月 10 日检索.
  22. Chisholm, Hugh (编) (1911 年). 《无穷小微积分 § 历史》. 《大英百科全书》第 14 卷（第 11 版）. 剑桥大学出版社. 第 537 页.
  23. Weil, André (1984 年). 《数论：从汉谟拉比到勒让德的历史路径》. 波士顿: Birkhauser Boston. 第 28 页. ISBN 0-8176-4565-9.
  24. Hollingdale, Stuart (1991 年). 《评〈牛顿之前：艾萨克·巴罗的生平与时代〉》. 《伦敦皇家学会笔记与记录》第 45 卷第 2 期，第 277–279 页. doi:10.1098/rsnr.1991.0027. ISSN 0035-9149. JSTOR 531707. S2CID 165043307. （评论节选：）"最引人注目的是第十至十二讲，巴罗在此近乎以几何方法证明了微积分基本定理……但他未完全意识到其成果的意义，且对代数的排斥使其工作仅成为 17 世纪中叶几何分析的历史注脚。"
  25. Bressoud, David M. (2011 年). 《积分基本定理教学的历史反思》. 《美国数学月刊》第 118 卷第 2 期，第 99 页. doi:10.4169/amer.math.monthly.118.02.099. S2CID 21473035.
  26. Blank, Brian E.; Krantz, Steven George (2006 年). 《单变量微积分（第一卷）》（插图版）. Springer Science & Business Media. 第 248 页. ISBN 978-1-931914-59-8. 存档于 2023 年 3 月 1 日. 于 2017 年 8 月 31 日检索.
  27. Ferraro, Giovanni (2007 年). 《级数理论的兴起与发展（至 19 世纪 20 年代初）》（插图版）. Springer Science & Business Media. 第 87 页. ISBN 978-0-387-73468-2. 存档于 2023 年 3 月 1 日. 于 2017 年 8 月 31 日检索.
  28. Guicciardini, Niccolò (2005 年). 《艾萨克·牛顿〈自然哲学的数学原理〉首版（1687 年）》. 载于《西方数学里程碑著作 1640–1940》. Elsevier. 第 59–87 页. doi:10.1016/b978-044450871-3/50086-3. ISBN 978-0-444-50871-3. （节选：）"[牛顿]立即意识到求积问题（逆问题）可通过无穷级数处理：用现代术语说，即展开被积函数为幂级数并逐项积分。"
  29. Grattan-Guinness, I. (编) (2005 年). 《西方数学里程碑著作 1640–1940》. 阿姆斯特丹: Elsevier. ISBN 0-444-50871-6. OCLC 60416766.
  30. Leibniz, Gottfried Wilhelm (2008 年). 《莱布尼茨早期数学手稿》. Cosimo, Inc. 第 228 页. ISBN 978-1-605-20533-5. 存档于 2023 年 3 月 1 日. 于 2022 年 6 月 5 日检索.
  31. Mazur, Joseph (2014 年). 《符号的启示：数学符号简史及其隐藏力量》. 普林斯顿大学出版社. 第 166 页. ISBN 978-0-691-17337-5. （节选：）"莱布尼茨深谙符号的概念力量与局限。他花费数年试验符号——调整、舍弃、与所有相识者通信，并请教当时所有同情其严谨性的顶尖数学家。"
  32. Frautschi, Steven C.; Olenick, Richard P.; Apostol, Tom M.; Goodstein, David L. (2007 年). 《机械宇宙：力学与热学》（进阶版）. 剑桥: 剑桥大学出版社. ISBN 978-0-521-71590-4. OCLC 227002144.
  33. Schrader, Dorothy V. (1962 年). 《牛顿与莱布尼茨关于微积分发现权的争论》. 《数学教师》第 55 卷第 5 期，第 385–396 页. doi:10.5951/MT.55.5.0385. ISSN 0025-5769. JSTOR 27956626.
  34. Stedall, Jacqueline (2012 年). 《数学史：极简导论》. 牛津大学出版社. ISBN 978-0-191-63396-6.
  35. Stenhouse, Brigitte (2020 年 5 月). 《玛丽·萨默维尔早期对微分微积分传播的贡献》(PDF). 《数学史》第 51 卷，第 1–25 页. doi:10.1016/j.hm.2019.12.001. S2CID 214472568.
  36. Allaire, Patricia R. (2007 年). 前言. 载于《玛丽亚·加埃塔纳·阿涅西传：一位 18 世纪女性数学家》. Antonella Cupillari 著. 刘易斯顿: Edwin Mellen Press. 第 iii 页. ISBN 978-0-7734-5226-8.
  37. Unlu, Elif (1995 年 4 月). 《玛丽亚·加埃塔纳·阿涅西》. Agnes Scott College. 存档于 1998 年 12 月 3 日. 于 2010 年 12 月 7 日检索.
  38. Bell, John L. (2013 年 9 月 6 日). 《连续性与无穷小》. 《斯坦福哲学百科全书》. 存档于 2022 年 3 月 16 日. 于 2022 年 2 月 20 日检索.
  39. Russell, Bertrand (1946 年). 《西方哲学史》. 伦敦: George Allen & Unwin Ltd. 第 857 页. （节选：）"十七世纪的伟大数学家们乐观且急于求成，因而留下了解析几何与无穷小微积分的基础不稳固。莱布尼茨相信实无穷小，尽管这一信念符合其形而上学，但数学上并无可靠根基。19 世纪中叶后不久，魏尔斯特拉斯展示了如何在不使用无穷小的情况下建立微积分，最终使其在逻辑上严密。随后，康托尔发展了连续性理论与无穷数。在他定义之前，'连续性'一直是个模糊术语，被黑格尔等哲学家用以将形而上学的混乱引入数学。康托尔赋予该词精确含义，并表明他所定义的连续性正是数学家与物理学家所需的概念。借此，柏格森等的神秘主义学说被扫入故纸堆。"
  40. Grabiner, Judith V. (1981 年). 《柯西严格微积分的起源》. 剑桥: MIT Press. ISBN 978-0-387-90527-3.
  41. Archibald, Tom (2008 年). 《数学分析严格性的发展》. 载于 Timothy Gowers、June Barrow-Green、Imre Leader 编《普林斯顿数学指南》. 普林斯顿大学出版社. 第 117–129 页. ISBN 978-0-691-11880-2. OCLC 682200048.
  42. Rice, Adrian (2008 年). 《数学大事年表》. 载于 Timothy Gowers、June Barrow-Green、Imre Leader 编《普林斯顿数学指南》. 普林斯顿大学出版社. 第 1010–1014 页. ISBN 978-0-691-11880-2. OCLC 682200048.
  43. Siegmund-Schultze, Reinhard (2008 年). 《亨利·勒贝格》. 载于 Timothy Gowers、June Barrow-Green、Imre Leader 编《普林斯顿数学指南》. 普林斯顿大学出版社. 第 796–797 页. ISBN 978-0-691-11880-2. OCLC 682200048.
  44. Barany, Michael J.; Paumier, Anne-Sandrine; Lützen, Jesper (2017 年 11 月). 《从南锡到哥本哈根到世界：洛朗·施瓦茨及其分布理论的国际化》. 《数学史》第 44 卷第 4 期，第 367–394 页. doi:10.1016/j.hm.2017.04.002.
  45. Daubin, Joseph W. (2008 年). 《亚伯拉罕·鲁宾逊》. 载于 Timothy Gowers、June Barrow-Green、Imre Leader 编《普林斯顿数学指南》. 普林斯顿大学出版社. 第 822–823 页. ISBN 978-0-691-11880-2. OCLC 682200048.
  46. Kline, Morris (1990 年). 《古今数学思想（第三卷）》. 纽约: 牛津大学出版社. ISBN 978-0-19-977048-9. OCLC 726764443.
  47. von Neumann, J. (1947 年). 《数学家》. 载于 R. B. Heywood 编《心智之作》. 芝加哥大学出版社. 第 180–196 页. （再版于 F. Bródy、T. Vámos 编《诺伊曼文集》. 世界科技出版公司. 1995 年. 第 618–626 页. ISBN 981-02-2201-7.）
  48. Herman, Edwin; Strang, Gilbert; 等 (2017 年). 《微积分（第一卷）》. 德克萨斯州休斯顿: OpenStax. ISBN 978-1-938168-02-4. OCLC 1022848630. 存档于 2022 年 9 月 23 日. 于 2022 年 7 月 26 日检索.
  49. Cheng, Eugenia (2017 年). 《超越无穷：数学边界的远征》. Basic Books. 第 206–210 页. ISBN 978-1-541-64413-7. OCLC 1003309980.
  50. Salas, Saturnino L.; Hille, Einar (1971 年). 《微积分：单变量与多变量》. 马萨诸塞州沃尔瑟姆: Xerox College Pub. OCLC 135567.
  51. Hughes-Hallett, Deborah; McCallum, William G.; Gleason, Andrew M.; 等 (2013 年). 《微积分：单变量与多变量》（第 6 版）. 新泽西州霍博肯: Wiley. ISBN 978-0-470-88861-2. OCLC 794034942.
  52. Moebs, William; Ling, Samuel J.; Sanny, Jeff; 等 (2022 年). 《大学物理（第一卷）》. OpenStax. ISBN 978-1-947172-20-3. OCLC 961352944.
  53. 例如：
    • Mahoney, Michael S. (1990 年). 《巴罗的数学：在古代与现代之间》. 载于 M. Feingold 编《牛顿之前》. 剑桥大学出版社. 第 179–249 页. ISBN 978-0-521-06385-2.
    • Feingold, M. (1993 年 6 月). 《牛顿、莱布尼茨与巴罗：一种重释尝试》. 《Isis》第 84 卷第 2 期，第 310–338 页. Bibcode:1993Isis...84..310F. doi:10.1086/356464. ISSN 0021-1753. S2CID 144019197.
    • Probst, Siegmund (2015 年). 《莱布尼茨作为读者与第二发明者：巴罗与门戈利的案例》. 载于 Norma B. Goethe、Philip Beeley、David Rabouin 编《G.W. 莱布尼茨：数学与哲学的交互》. 《阿基米德：科学与技术史哲学新研究》第 41 卷. Springer. 第 111–134 页. ISBN 978-9-401-79663-7.
  54. Herman, Edwin; Strang, Gilbert; 等 (2017 年). 《微积分（第二卷）》. 休斯顿: OpenStax. ISBN 978-1-5066-9807-6. OCLC 1127050110. 存档于 2022 年 7 月 26 日. 于 2022 年 7 月 26 日检索.
  55. Baron, Margaret E. (1969 年). 《无穷小微积分的起源》. 牛津: Pergamon Press. ISBN 978-1-483-28092-9. OCLC 892067655.
  56. Kayaspor, Ali (2022 年 8 月 28 日). 《微积分在现实中的美妙应用》. Medium. 存档于 2022 年 9 月 26 日. 于 2022 年 9 月 26 日检索.
  57. Hu, Zhiying (2021 年 4 月 14 日). 《微积分在日常生活中的应用与价值》. 载于《2021 年第二届亚太图像处理、电子与计算机国际会议》. IPEC2021. 中国大连: ACM. 第 562–564 页. doi:10.1145/3452446.3452583. ISBN 978-1-4503-8981-5. S2CID 233384462.
  58. Kardar, Mehran (2007 年). 《粒子统计物理学》. 剑桥大学出版社. ISBN 978-0-521-87342-0. OCLC 860391091.
  59. Garber, Elizabeth (2001 年). 《物理学的语言：微积分与欧洲理论物理学发展（1750–1914）》. Springer Science+Business Media. ISBN 978-1-4612-7272-4. OCLC 921230825.
  60. Hall, Graham (2008 年). 《麦克斯韦电磁理论与狭义相对论》. 《哲学学报：数理与工程科学》第 366 卷第 1871 期，第 1849–1860 页. Bibcode:2008RSPTA.366.1849H. doi:10.1098/rsta.2007.2192. ISSN 1364-503X. JSTOR 25190792. PMID 18218598. S2CID 502776.
  61. Gbur, Greg (2011 年). 《光学物理与工程的数学方法》. 剑桥: 剑桥大学出版社. ISBN 978-0-511-91510-9. OCLC 704518582.
  62. Atkins, Peter W.; Jones, Loretta (2010 年). 《化学原理：洞察的追寻》（第 5 版）. 纽约: W.H. Freeman. ISBN 978-1-4292-1955-6. OCLC 501943698.
  63. Murray, J. D. (2002 年). 《数学生物学（卷一）：导论》（第 3 版）. 纽约: Springer. ISBN 0-387-22437-8. OCLC 53165394.
  64. Neuhauser, Claudia (2011 年). 《生物与医学微积分》（第 3 版）. 波士顿: Prentice Hall. ISBN 978-0-321-64468-8. OCLC 426065941.
  65. Gatterdam, R. W. (1981 年). 《作为格林定理实例的求积仪》. 《美国数学月刊》第 88 卷第 9 期，第 701–704 页. doi:10.2307/2320679. JSTOR 2320679.
  66. Adam, John A. (2011 年 6 月). 《血管分支：超越标准微积分问题》. 《数学杂志》第 84 卷第 3 期，第 196–207 页. doi:10.4169/math.mag.84.3.196. ISSN 0025-570X. S2CID 8259705.
  67. Mackenzie, Dana (2004 年). 《数学建模与癌症》(PDF). 《SIAM 新闻》第 37 卷第 1 期. 存档(PDF)于 2022 年 10 月 9 日.
  68. Perloff, Jeffrey M. (2018 年). 《微观经济学：理论与微积分应用》（第 4 全球版）. 哈洛: Pearson. ISBN 978-1-292-15446-6. OCLC 1064041906.

7. 扩展阅读

8. 外部链接


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利